藏族傳統天文歷算中日月位置計算方法研究
索郎桑姆, 羅布頓珠 ,格 朗,南木加
(1.《西藏大學學報》編輯部,西藏 拉薩 850000;2.西藏藏醫藥大學,西藏 拉薩 850000)
0 引言

1 日月平動情況
1.1 積月

1.1.1 算法
積月的算法口訣:計算所求年份在第17勝生周中已過的年數,乘12再加所求月數,所得結果重張兩位,自下而上(2)藏歷中把同一度量系統中大小不同單位的數碼由上而下分開列出來,它們共同的乘數則相應地重復書寫,這種寫法在《九執歷》中譯為“重張位”.,下位乘2再除65,以其商加上位.
據此可算出從歷年至藏歷水蛇年的積月:

(1)
312+9=321
(2)
312×2=624/65=9……39
(3)
1.1.2 歷算依據
1.2 曜基數

1.2.1 算法
曜基數的算法口訣:月重張五位,自上而下分別為曜位、漏刻位、漏分位、息位、分子位以及分母位;曜位乘1,漏刻位乘31,漏分位乘50,息位乘0,分子位乘45,分母乘345;再自上往下加3、11、50、0、31和327;所得結果從下位往上除以707、67、6、60、60和7進位,所得余數為曜基數.
具體算式:
321×1=321+3=324+170=494/7=70……4曜
(4)
321×31=9951+11=9962+268=10230/60=170……30漏刻
(5)
321×50=16050+27=16067+36=16103/60=268……23漏分
(6)
321×0=0+2=2+218=220/6=36……4息
(7)
321×45=14445+31=14476+157=14633/67=218……27日若恰
(8)
321×345=110745+327=111072/707=157……23日喀日恰
(9)
1.2.2歷算依據
根據時輪歷中的年月日之間關系可知,一個太陰月的長度為29個太陽日31漏刻50漏分0息345日若恰,一個太陰月結束時的值日曜為日曜(6)周序日名:0土曜、1日曜、2月曜、3火曜、4水曜、5木曜、6金曜.29/7=4余1,舍去商數,取余1,即日曜.[3].因此,積月乘以一個太陰月的長度,再加上第17勝生周歷元平朔時太陰日的結束時刻(3太陽日11漏刻27漏分2息31日若恰327日喀日恰),得到所求月平朔時刻的值日曜為第4曜水曜,且該太陰日結束時刻為30漏刻23漏分4息27日若恰23日喀日恰.
1.3 整數和零數
1.3.1 算法
整數和零數的算法口訣:置積月重張兩位,上位乘2,下位乘1,上位恒加21,下位恒加90,再下位除以126,所得商數加上位后再除28,上下位余數為整數與零數.
具體算式:
321×2=663+3=642+21(7)《時輪精要》記載,第16勝生周結束時剩余的整數為21.=666/28=23……22個整數
(10)
321×1=321+90(8)《時輪精要》記載,第16勝生周結束時剩余的零數為90.=411/126=3個整數……33個零數
(11)
1.3.2 天文學依據
月亮在以二十八宿為代表的恒星背景中以近地點為起點,連續兩次通過近地點時月亮所走的路程在時輪歷中用28個整數來表示,一個太陰月內月亮從近地點出發除了走完28個整數外,再多走2個整數和1/126個整數(即零數).根據式(10)~(11)可知,所求月平朔時月亮已經在星空背景中從近地點出發又回到近地點的次數為23次,再多走了22個整數和33個零數.
1.4 日曜基數

1.4.1 算法
日曜基數算法口訣:積月重張五位,自上而下分別為宿位、漏刻位、漏分位、息位及子位,宿位乘2,漏刻位乘10,漏分為乘58,息位乘1,分子位乘17;再自宿位到息位分別加58、311、67、81;最后自下而上分別除以67、6、60、60及27進位(9)由于月亮在其朔望一周的時間間隔內剛好在27星宿為背景的天空中循環一周,因此把一周天均分為27宿,1宿=60弧刻,1弧刻=60弧分,1弧分=6弧息,1弧息=67日若恰.,所得余數為日曜基數.
可算出藏歷水蛇年3月平朔時的日曜基數:
321×2=642+58=700/27=25……25宿
(12)
321×10=3210+311=3521/60=58宿……41弧刻
(13)
321×58=18618+67=18685/60=311弧刻……25弧分
(14)
321×1=321+81=402/6=67弧分……0息
(15)
321×17=5457/67=81息……30日若恰
(16)
1.4.2 天文學依據

1.5 中曜和中日

1.5.1 算法
日曜和中日的算法口訣:以59漏刻3漏分4息1日若恰365日喀日恰,乘以所求之日的日期,再加曜基數得中曜;以4弧刻21分5息43日若恰乘以所求日序數加日曜基數得中日.
中曜的算式:
4+0=4+1=5宿
(17)
30+45=75+1=76/60=1……16漏刻
(18)
23+55=78/60=1……18漏分
(19)
4+0=4息
(20)
27+22=49日若恰
(21)
23+526=549日喀日恰
(22)
中日的算式:
25+1=26宿
(23)
41+5=46弧刻
(24)
25+29=54弧分
(25)
0+0+1=1息
(26)
30+42=72/67=1……5日若恰
(27)
1.5.2 天文學依據
1.5.2.1 中曜
所求的具體日期乘以一個太陰日的長度(59漏刻3漏分4息1日若恰365日喀日恰)[3],得到當月1~15日值日曜循環2次后至0曜,該太陰日結束時刻為45漏刻55漏分0息22日若恰526日喀日恰.該值加上已求出的曜基數,得到所求太陰日的曜次為第5曜,該太陰日結束時刻為16漏刻18漏分4息49日若恰549日喀日恰.
所求日期乘以一個太陰日內太陽所行的路程(4弧刻21弧分5息43日若恰)[3],得到本月1~15日太陽所行的平均路程為:1宿5弧刻29弧分0息42日若恰.該值加上日曜基數(25宿41弧刻25弧分0息和30日若恰),得出所求太陰日結束時,太陽距白羊宮首的弧長(太陽的平黃經)為26宿46弧刻54弧分1息5日若恰.
至此,已經算出從歷元至藏歷水蛇年3月15日太陽和月亮的平均行度.但是,太陽系里所有天體,都有視運動的快慢變化,包括太陽在內,因此,還需要算出月亮和太陽的真黃經.
2 慮及日月的不均勻運動
2.1 月離步數表

表1 月離步數表
2.2 曜凈行(月步)
2.2.1 算法

具體算式:
22+15=37/14=2……9個整數
(28)
33×3=99/126=0弧刻……99
(29)
99×60=5940/126=47弧分……18
(30)
18×6=108/126=0息……108
(31)
108×67=2136/126=57日若恰……54
(32)
54×707=38178/126=303日喀日恰……0
(33)
2.2.2 天文學依據

2.3 半定曜
2.3.1 算法

具體算式:
22-0-1=21
(34)
60-47=13-1=12
(35)
6-0=6-1=5
(36)
67-57=10-1=9
(37)
707-303=404
(38)
所求出的月步值加上已求出的中曜值(5曜16漏刻18漏分4息49日若恰549日喀日恰)得到半定曜:
16+21=37漏刻
(39)
18+12+1=31漏分
(40)
4+5=9/6=1漏分……3息
(41)
49+9+1=59/67=0息……59日若恰
(42)
549+404=953/707=1日若恰……246日喀日恰
(43)
至此,已求出半定曜的值為5曜37弧刻31弧分3息59日若恰和246日喀日恰.
2.3.2 天文學依據
月球在白道上從近地點開始運動,運動速度逐漸加快,到達遠地點時速度達到最大值,往后速度逐漸減小,回到近地點時速度達到最小值.本文得出15日時月亮在周天范圍內已走完第9個整數,并在第10個整數之內走了33個零數,落在后步范圍之內,意味著月步比平均值快.查表1可知,月球從近地點開始運動到走完第9步,各步的損益率累積之和為22弧刻(盈縮積),并且在第10個整數內月亮比平均值多行了0弧刻47弧分0息57日若恰303日喀日恰,因此盈縮積減去第10個整數內比平均值多行的距離,可得出月亮從近地點開始運動到所求日時,月亮實際比平均值多行的距離為21弧刻12弧分5息9日若恰404日喀日恰.根據月亮的平均行度,已經求出所求日的值日曜為第5曜,并且該太陰日的結束時刻為16漏刻18漏分4息49日若恰549日喀日恰(中曜).中曜值加上月亮從近地點開始運動到所求太陰日實際比平均值多行的距離,得到所求日值日曜為第5曜,該太陰日的結束時間為37漏刻31漏分3息59日若恰246日喀日恰(12)月步(月亮的真盈縮弧長)的單位是弧刻,中曜(太陰日結束的時刻)的單位是漏刻,單位不同,本不能相加減,此處因二者周期相差很小,幾乎相等,就簡單地直接進行加減了..
2.4 日躔步度表

表2 日躔步度表

2.5 太陽凈行
2.5.1 算法

具體算式:
26-6=20-1=19-13=6×60+31=391/135=2宮……121弧刻
121/135=0……121弧刻
(44)
46-45=1+60=61-30=31弧刻
(45)
54×1=54 121×60+54=7314/135=54……24弧分
(46)
1×1=1 24×6+1=145/135=1……10息
(47)
5×1=5 10×67+5=675/135=5日若恰
(48)
由上式算出太陽在第3宮內多行了54弧分1息5日若恰,再加上此時的盈縮積10弧刻(見表2),得出所求日太陽凈行值為10弧刻54弧分1息5日若恰.
2.5.2 天文學依據
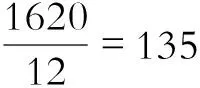
2.6 定曜與定日
2.6.1 算法

具體算式:
定耀
5
(49)
37+10=47+1=48漏刻
(50)
31+54=85/60=1……25漏分
(51)
3+1=4息
(52)
59×707+29=41742/67=623……1 623+5=628日喀日恰
(53)
定日
26
(54)
46+10=56+1=57弧刻
(55)
54+54=108/60=1……48弧分
(56)
1+1=2息
(57)
5+5=10日若恰
(58)
2.6.2 歷法依據
定曜為真太陰時刻,即所求日準確的曜日序數和該太陰日結束時刻[4].本文已求出所求日的值日曜為第5曜,且該太陰日的結束時間為37漏刻31漏分3息59日若恰29日喀日恰(半定曜),此時已經計入了月行疾遲的影響,但未計入日月盈縮的影響.因此,還需在半定曜基礎上加上太陽凈行值(10弧刻54弧分1息5日若恰),得到所求日的定曜,即該日值日曜為第5曜,該太陰日的結束時刻為48漏刻25漏分4息628日喀日恰.
定日為所求太陰日結束時,太陽所在之宿和在該宿內所行的弧度數,即太陽的真黃經.本文已經求出太陽凈行弧刻為10弧刻54弧分1息5日若恰,亦已求出中日值為26宿46弧刻45弧分1息5日若恰.將以上兩值相加得到所求日太陰日結束時刻太陽的真黃經,26宿57弧刻48弧分2息10日若恰.因此,所求日的值日曜為第5曜即水曜,定日為壁宿.
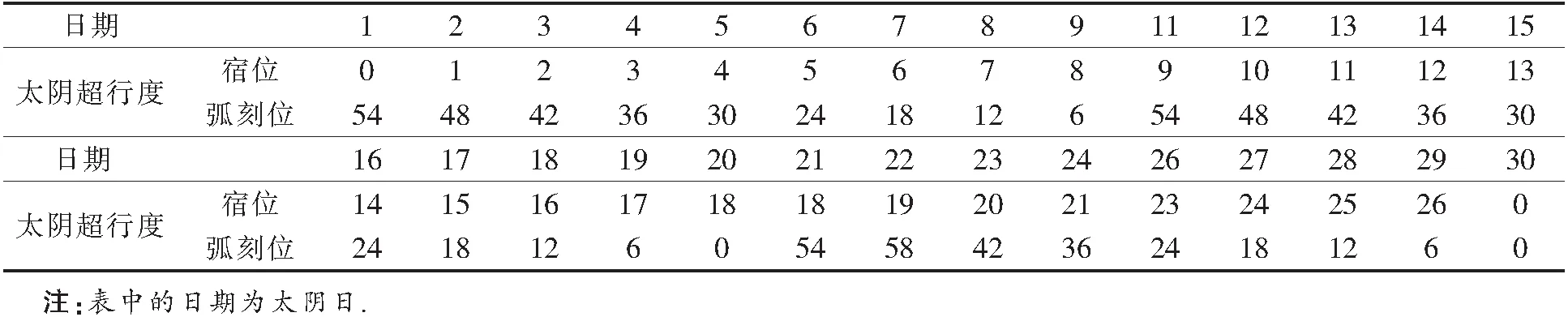
表3太陰超行度表
2.7 太陰超行度表
2.8 太陰日月宿
2.8.1 算法
太陰日月宿算法口訣:置定日的宿位與弧刻位,重張兩位,分別加上太陰日超行度表中所求日太陰超行度值,再分別除以弧刻位和宿位周期進位,得太陰日月宿.
具體算式:
26+13=39+1=40/27=1……13宿
(59)
57+30=87/60=1……27弧刻
(60)
48弧分
(61)
2息
(62)
10日若恰
(63)
2.8.2 天文學依據

2.9 曜伴月宿(太陽日月宿)

2.9.1 算法
太陽日月宿算法口訣:太陰日月宿值減去定耀,得到太陽日月宿.
具體算式: 13-1=12宿
(64)
27+60-48=39弧刻
(65)
48-25=23-1=22弧分
(66)
2+6-4=4-1=3息
(67)
10+707-628=89日喀日恰
(68)
2.9.2 天文歷法依據

結語


