66 千伏組合電器局部放電實驗干擾抑制研究

包育瑋 王鏡賀 甘 旭 劉昊軒（國網盤錦供電公司，遼寧 盤錦 124000）

局部放電所引發的物理化學反應會對材料的絕緣性能造成緩慢的損害，因此進行局部放電檢測十分必要，通過局部放電檢測發現絕緣缺陷，能夠保證高壓組合電器的安全、穩定、可靠運行[1]。局部放電檢測主要涵蓋了兩方面主要內容，即局部放電信號的提取和干擾信號的抑制。

1 局部放電基本理論

1.1 局部放電信號數學模型

通常情況下，局部放電的脈沖電流持續時間非常短，通常只有ns 等級，并且其頻帶范圍較寬，如圖1 所示為典型的局部放電脈沖電流波形[2]。

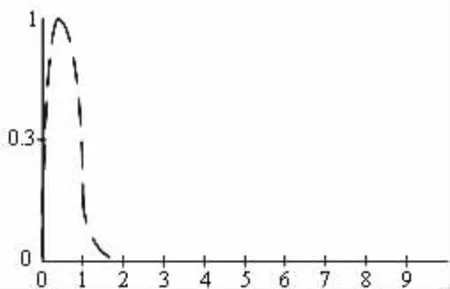
圖1 局部放電脈沖電流典型波形

局部放電脈沖電流的波形由絕緣缺陷的類型決定，但也會受到其它因素的影響。檢測到的局部放電信號中通常混有大量的干擾信號，為了便于進行研究，采用指數衰減脈沖和震蕩衰減脈沖來模擬局部放電信號，兩種脈沖信號可以用公式（1）、公式（2）來描述：

其中，M為脈沖信號的最大值，θ1和θ2為時間常數，fc為震蕩衰減脈沖的震蕩頻率。如圖2 所示為由指數衰減脈沖模擬的局部放電信號波形。

圖2 局部放電信號模擬波形

1.2 局部放電檢測方法

局部放電會引發許多物理、化學現象，局部放電檢測就是測量局部放電過程中的物理量，對局部放電狀態進行描述，常規的檢測方法有脈沖電流法、超高頻法、超聲波法[3]。

脈沖電流法的靈敏度較高，并且能夠實現對放電量的測量；超高頻法具有很強的抗干擾能力，并且能夠實現對放電位置的診斷；超聲波法的檢測靈敏度較低，并且抗干擾能力較差，極容易受到強電磁場的干擾，不能實現對放電量的測量，通常用于對放電位置的定位。綜合來看，每一種方法都有其各自的優缺點，應當進行綜合考慮，采用多種方法對局部放電進行測量，得到最優的測量結果。

2 局部放電信號干擾抑制策略

2.1 小波變換理論

小波變換的作用是實現信號從時域到時頻域的變換，能夠將信號表現為源自于小波函數θ（t）經過平移、伸縮變換得到的信號的疊加，正是基于小波變換平移和伸縮特性，小波變換同時適用于時域和頻域的分析。

小波變換定義為：θ（t）∈L2（R），其對應的傅立葉變換為θ（ω）。當θ（ω）滿足條件：

利用小波變換進行信號分析時，時間分辨率和頻率分辨率都是可以根據實際需求調節的，在頻率分辨率較高的部分具有較低的時間分辨率，在頻率分辨率較低的部分具有較高的時間分辨率。小波變換將信號進行全頻段、全時段的細致描述，能充分體現信號的全部細節。

2.2 小波特性分析

假定函數f（x）在某一點處的正則性可以通過利普希茨指數σ 來描述，如果利普希茨指數的值較大，則函數的形狀相對平滑。

定理：假設σ∈[0，1]，并且f（x）∈L2（R），[m，n]為R 上的一個區間，有且僅有對任意x∈[m，n]，存在常數ρ，使得|Wf（s，x）|≤ρsσ成立，則稱f（x）是在區間[m，n]上的一致性利普希茨指數。

信號在多個尺度上的小波分解參數的最大模值與利普希茨指數存在對應關系，如果利普希茨指數為正，則隨著尺度的變大，最大模值也對應變大；如果利普希茨指數為零，則最大模值與尺度的變化不存在明顯關聯性；如果利普希茨指數為負，則隨著尺度的變小，最大模值也對應變大，正好與利普希茨指數為正的情況完全相反。

局部放電信號的利普希茨指數為：0<σ<1。所以局部放電信號的最大模值隨著分解尺度的變大而變大。

干擾信號的利普希茨指數為：σ=-0.5-υ，υ>0，所以干擾信號的最大模值隨著分解尺度的變大而變小。

假設干擾信號n（k）的期望值為零，方差為ξ，干擾信號為寬平穩信號，Wn（j，k）為干擾信號n（k）的小波變換結果，小波θ（k）為實數函數，存在θj（k）=2jθ（2jk），則存在：

公式（10）表明平均功率與尺度呈現反比例關系，也就印證了干擾信號的模極大值隨著分解尺度的變大而變小。

通過以上對利普希茨指數的分析可以得到結論：局部放電信號的利普希茨指數為正，干擾信號的利普希茨指數為負，他們的最大模值隨著尺度的變大，呈現出完全相反的變化特性，干擾信號的小波參數隨著尺度的變化被顯著區分開，這就為通過小波變換方法抑制干擾信號提供了理論依據。

2.3 改進型干擾抑制策略

空間域相關理論認為經過小波變換后的信號，得到的小波參數在不同的尺度上都具有關聯性，特別是在信號邊緣地帶，關聯性更為顯著，而干擾信號對應的小波參數則不存在這種關聯性。因此可以通過小波參數在不同尺度對應點上的關聯性來確定是有效信號還是干擾信號，這樣進行分解處理后，小波參數與信號邊緣存在對應關系。

改進型干擾抑制策略的原理為，信號的突變位置在不同尺度下的同一位置都存在極大值，干擾信號的能量隨著尺度的變大而減小。由此，可以提取臨近尺度的小波參數進行乘法運算，從而將強化信號邊緣及其他重要特征信號的同時抑制干擾信號。

定義1：

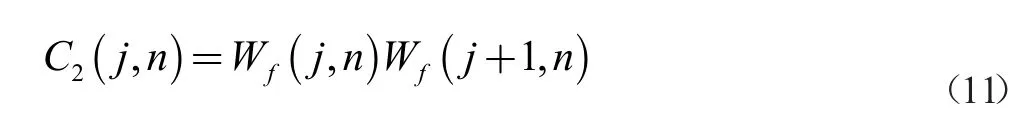
其中，C2（j，n）表示尺度j 中位置n 處的關聯參數，Wf（j，n）表示尺度j 中位置n 處干擾信號的離散小波變換。為了保證關聯參數與小波參數便于對比分析，對相關變量進行歸一化處理。

定義2：

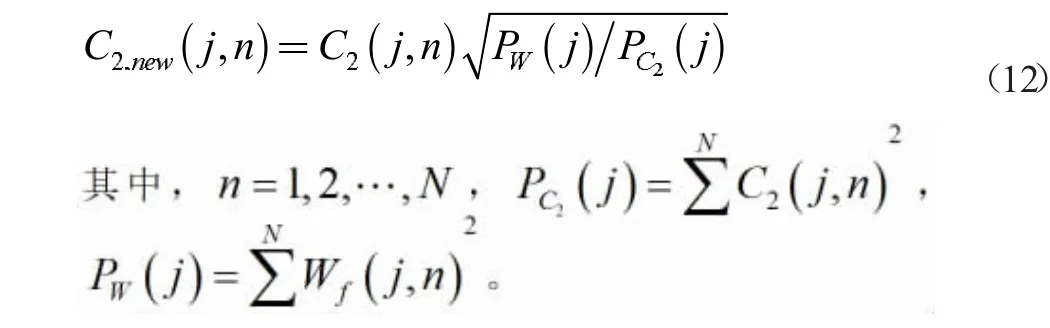
通過比較|C2.enw（j，n）| 和|Wf（j，n）| 的大小來區別信號的重要邊緣地帶，如果前者大于后者，則認為該點與信號的邊緣相對應，保存Wf（j，n）的位置和幅值，并將C2.new（j，n）和Wf（j，n）中的相應位置清零，否則該點就與干擾信號對應，將剩余數據重新進行標記，多次重復進行上述過程，直到Wf（j，n）中沒有被抽取的點的能量小于該尺度上的干擾信號能量時，終止抽取。這樣就實現了有效信號的提取和干擾信號的抑制。

3 仿真驗證

經實際檢測發現，局部放電信號多數情況下呈現震蕩衰減脈沖的變化趨勢，由于其震蕩特性，其干擾信號的抑制相對困難一些，在進行局部放電仿真的時候，將原始信號的幅值進行歸一化處理，其信號波形如圖3 所示。

圖3 局部放電原始信號

分別采用傳統干擾信號抑制策略和改進型干擾信號抑制策略對局部放電信號中的干擾信號進行抑制，對比傳統型和改進型干擾信號抑制策略，明顯可以發現改進型干擾信號抑制策略干擾抑制效果更好，不僅能濾除傳統型抑制策略沒有濾除的干擾，更為關鍵的是，沒有多余的能量損失。

4 結論

本文基于小波理論的角度展開研究，將小波閾值算法與空域理論相結合，對局部放電信號中的干擾信號進行了抑制。經過仿真驗證，結果表明本文提出的改進型干擾抑制策略更為先進，能夠在強烈的干擾環境下，將局部放電信號進行有效提取，干擾信號濾除后能量損失較小，尖峰特征保留較好，峰值下降得也比較小，該算法的干擾抑制效果較為顯著。