基于子單元光滑有限元的混凝土相場損傷模型研究

吳卓恒

（華南理工大學土木與交通學院，廣東 廣州 510641）

混凝土是當今應用最為廣泛的工程材料之一，然而作為一種準脆性材料，其在正常使用中會不可避免的出現裂縫，雖然現行《混凝土結構設計規范》[1]允許鋼筋混凝土構件帶裂縫工作，但這些裂縫則對構件乃至結構造成的不利影響仍是不可忽略的。

2018 年，Wu 提出的混凝土相場損傷模型[1]在給定相場尺度參數b 后僅需彈性模量、泊松比、單軸抗拉強度等容易獲取的材料參數即可很好地模擬混凝土中復雜的開裂行為，有很廣闊的應用前景。但該模型在通過有限元方法（Finite Element Method，FEM）進行求解時，由于需要保證相場梯度的精度，在潛在開裂區域附近往往需要劃分較為精細的網格，這導致模型分析效率偏低。

2007 年Liu 等結合無網格法中的光滑應變技術，提出了光滑有限元方法（Smoothed FEM, S-FEM）[3]，其中子單元光滑有限元（Cell-based S-FEM, CS-FEM）算法簡單，且在同網格下較FEM具有更高的計算精度。用其求解混凝土相場損傷模型的位移場與相場將有望提升求解精度，降低其對網格尺寸的要求，提升分析效率。

基于以上考慮，本工作將使用CS-FEM來求解混凝土相場損傷模型的位移場與相場，驗證其求解相場損傷模型的能力，同時比較CS-FEM 在建議網格尺寸下的細網格和建議網格尺寸外的粗網格模擬結果的差異。

1 混凝土相場損傷模型

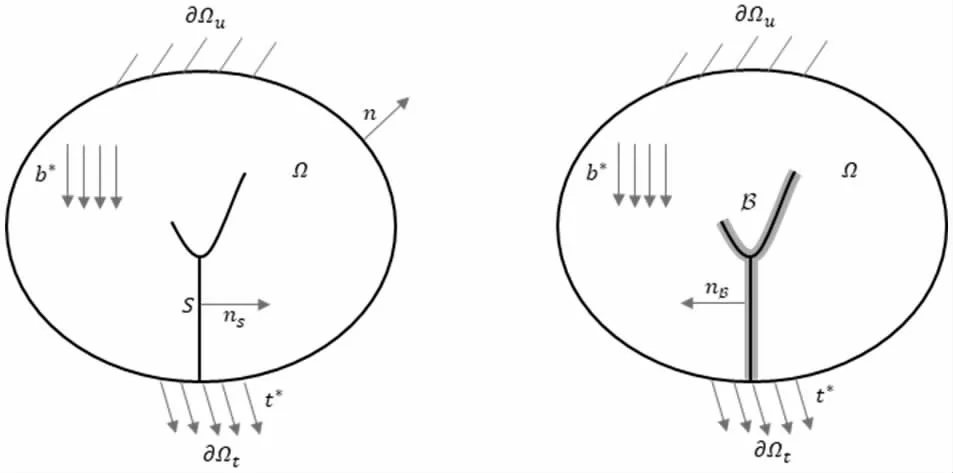
圖1 混凝土相場損傷模型對裂縫的幾何規則化

在混凝土相場損傷模型中，尖銳裂縫S 被彌散至寬度由尺度參數b 控制的損傷帶B 中，固體其余部分ΩB 則不受裂縫影響。根據[1，3，4]，混凝土相場損傷模型的相關公式可整理為表1 所示的公式方框圖。

表1 混凝土相場損傷模型公式

在混凝土相場損傷模型基于FEM的數值實現中，為保證求解精度，一般建議網格尺寸h 與相場長度尺度參數b 滿足h≤b/5。

2 CS-FEM 基礎理論與數值實現

2.1 光滑應變技術

在標準FEM中，固體的應變通過以下公式計算

式中，Nn為模型中的節點總數，Ni為節點i 的位移插值形函數矩陣，ai為節點i 的所有位移自由度。

CS-FEM中采用的光滑應變技術則是在標準有限元應變場的基礎上進行空間平均化處理。將求解區域劃分為Ns個光滑域Ωsk，采用常數型光滑函數[6]，根據高斯公式可以得到邊界上一維線積分形式的光滑應變場計算公式

式中，nx和ny分別為邊界Γsk單位外法向量沿x 軸和y 軸方向的分量。

2.2 混凝土相場損傷模型在CS-FEM中的實現

CS-FEM中位移場與相場的通過以下的插值公式計算

式中，Nui和Ndi為節點位移和相場的插值形函數矩陣，aui和adi分別為節點i 的所有位移自由度和相場自由度。

如圖2 所示，CS-FEM 的光滑域是通過連接兩條對邊的中點得到的。相應的光滑后的應變和相場梯度表達式為

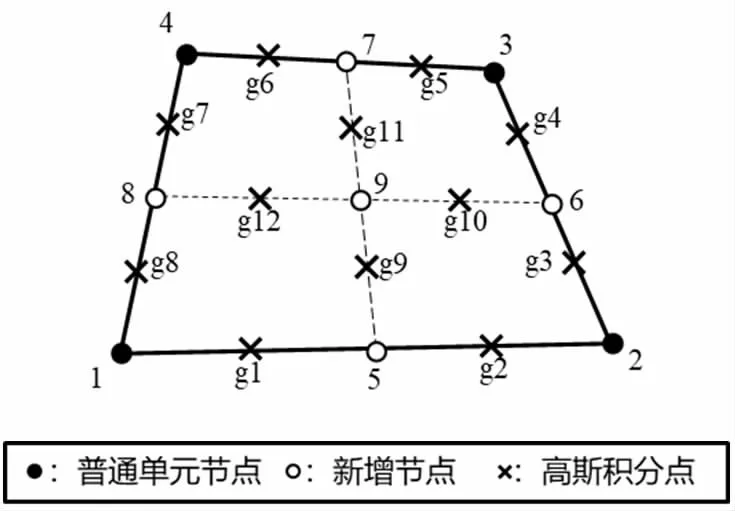
圖2 CS-FEM 中的光滑域劃分與積分的分布

式中，NsΓ為光滑域的邊界數；xGp為邊界上高斯積分點的坐標；lp為積分邊界的長度。需要指出的是，整個過程不需要標準有限元中對單元插值形函數的求導以及單元的等參變換。

通過上述的離散過程，可以得到殘量形式的控制方程

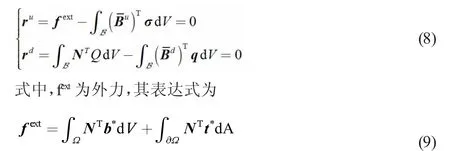
3 數值算例

考慮Winkler[7]的L 型板試驗，試件的幾何尺寸、加載方式與裂縫路徑如圖3 所示。模擬中采用Unger 等[7]建議的材料參數：彈性模量E0=2.0×104MPa，泊松比υ=0.18，單軸抗拉強度ft=2.5MPa，Ⅰ型斷裂能Gf=0.130N/mm。相場長度尺度參數b 取為10mm。分別考慮大于建議網格尺寸的粗網格（h = b/2）和滿足建議網格尺寸外的細網格（h = b/5）。

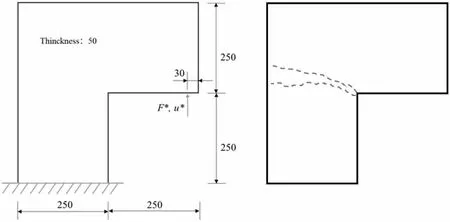
圖3 L 型板試驗：幾何尺寸、加載方式與裂縫路徑

模擬得到的開裂路徑如圖4 所示，可以看出基于CS-FEM的相場損傷模型在粗、細網格下得到的裂縫路徑相同，且落在試驗實測范圍內。

圖4 模擬得到的開裂路徑

模擬得到的荷載- 位移曲線如圖5 所示，從中可以看出粗網格下得到的荷載較細網格下的結果偏大，但二者間差別很小且均落在試驗實測范圍內。

圖5 模擬和試驗得到的荷載- 位移曲線

4 結論

4.1 子單元光滑有限元（CS-FEM）能正確求解混凝土相場損傷模型。

4.2 CS-FEM在采用較FEM建議的網格尺寸（h≤b/5）更粗的網格（h=b/2）時同樣能正確地模擬混凝土開裂破壞過程。