橢圓函數(shù)在濾波器上的應(yīng)用
卓群忠
(福建廣播電視大學(xué)莆田分校,福建 莆田351100)
上世紀(jì)初,研究人員在雙模準(zhǔn)橢圓函數(shù)方面的研究上取得了一定的成果,同時(shí)將這一理論應(yīng)用在了濾波器的諧振單元中,形成了L型結(jié)構(gòu)耦合單元。新世紀(jì)初,Lung-Hwa Hsieh和Kai Chang等人的研究促進(jìn)了橢圓函數(shù)濾波器的發(fā)展,他們通過將圓環(huán)諧振器和間隙耦合發(fā)明了緊湊型的橢圓函數(shù)濾波器。沒過多久,Lung-Hwa Hsieh和Kai Chang等人又通過耦合臂和方形環(huán)搭配諧振電路設(shè)計(jì)出了L型支節(jié)耦合的雙模準(zhǔn)橢圓函數(shù)濾波器。之后,吳勝陽概括總結(jié)了橢圓函數(shù)低通濾波器的工作原理和設(shè)計(jì)方法,通過對(duì)MATLAB的仿真,結(jié)合橢圓函數(shù)的設(shè)計(jì)步驟,給出了一個(gè)能夠在微帶線上的橢圓函數(shù)低通濾波器設(shè)計(jì)方案。綜上,對(duì)于橢圓函數(shù)濾波器的研究并不少見。文章就橢圓函數(shù)的定義和推導(dǎo)出發(fā),介紹橢圓函數(shù)在濾波器中的應(yīng)用,以及橢圓函數(shù)的響應(yīng)特性,綜合闡述橢圓函數(shù)在濾波器方面的應(yīng)用及發(fā)展。
1 橢圓函數(shù)基本概念
1.1 橢圓函數(shù)
雅可比橢圓函數(shù)是橢圓濾波器的數(shù)學(xué)基礎(chǔ),通過積分的思想方法,借助勒讓德第一類橢圓積分導(dǎo)出其具體性質(zhì):
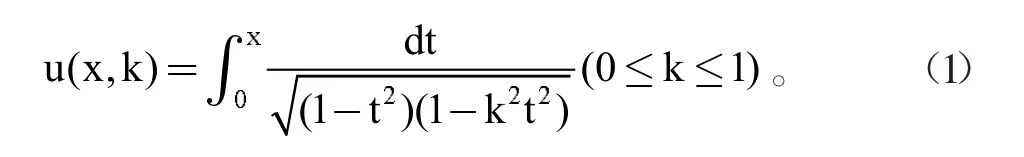
在我們研究的范圍內(nèi),參數(shù)k是小于1的實(shí)數(shù),稱為模數(shù),把t做如下代換:
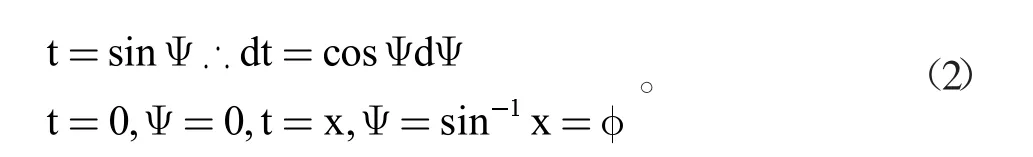
第一類橢圓積分可以推導(dǎo)出以下函數(shù):
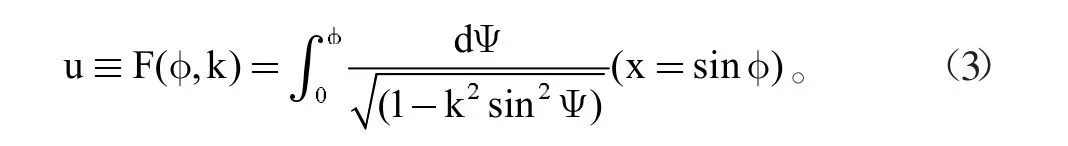
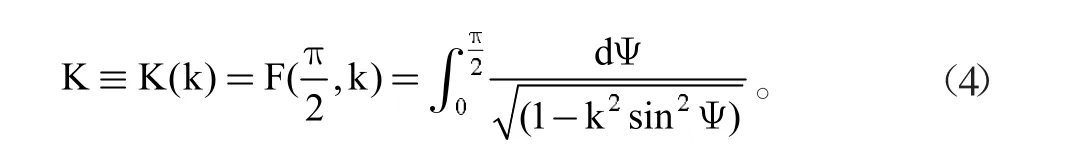
橢圓積分顧名思義,與橢圓的性質(zhì)有很大關(guān)系,具有對(duì)稱性,同時(shí)也具有周期性,因此任意實(shí)數(shù)k的函數(shù)值都能夠在0≤Ψ≤π/2周期內(nèi)的計(jì)分表中獲得。
要是把公式(2)的積分上限φ當(dāng)作是u和k的函數(shù),那么可以引入符號(hào):φ=am(u,k),其中φ稱為以k為模的u的幅度函數(shù),通過變換可以獲得x=sinφ=sin am(u,k),這就是以k為模的雅可比橢圓正弦函數(shù)。
1.2 橢圓函數(shù)的性質(zhì)
函數(shù):
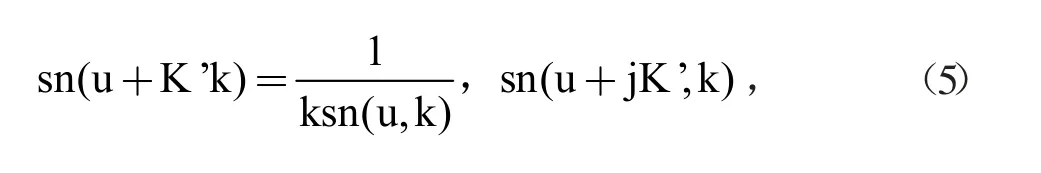
這個(gè)函數(shù)的極點(diǎn)是當(dāng)sn(u,k)的函數(shù)值為零的地方,此時(shí)u=0,因?yàn)閟n(u,k)=0,并且是關(guān)于4K和j2K'雙周期函數(shù),因此函數(shù)sn(u,k)的極點(diǎn)為2mK+j(2n+1)K',這里的n,m是一個(gè)整數(shù)。因?yàn)閚階橢圓函數(shù)具有低通的性質(zhì):
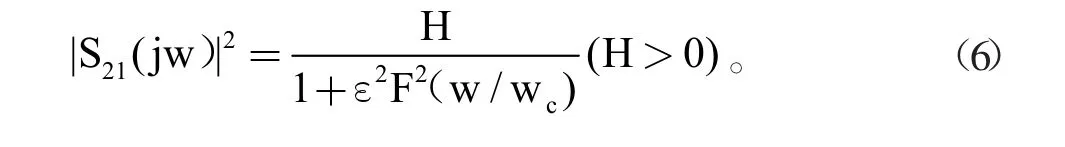
這個(gè)函數(shù)當(dāng)中,如果n是一個(gè)奇數(shù),那么這個(gè)函數(shù)的特征函數(shù)是:
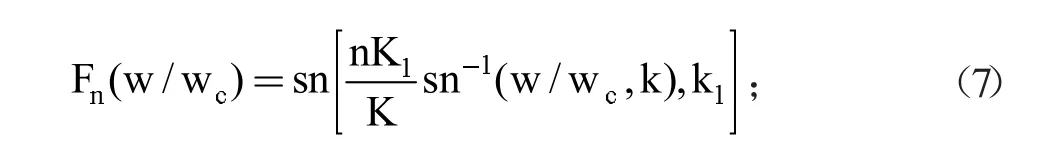
如果n是一個(gè)偶數(shù),那么這個(gè)函數(shù)的特征函數(shù)是:
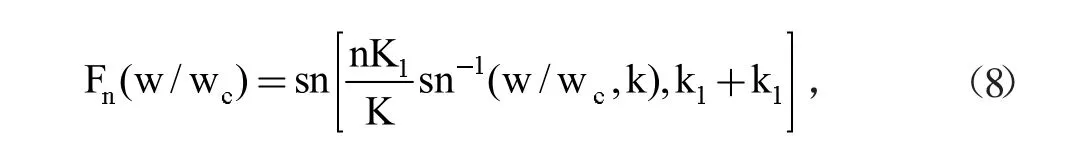
函數(shù)中K1=K(k1);K=K(k)被定義為全橢圓積分,這兩個(gè)函數(shù)的模為k1和k。Fn(w)是一個(gè)特征函數(shù),這里可以得到有理函數(shù)(這個(gè)有理函數(shù)是兩個(gè)含w的多項(xiàng)式比值),有理函數(shù)定義域范圍內(nèi)包含的零點(diǎn)完全落在阻帶范圍內(nèi),并且定義域內(nèi)的所有極點(diǎn)也全部在阻帶范圍內(nèi)。例如:令n=3,k=1/1.4=0.71429,可以獲得Fn(w),通過積分表可以獲得K=K(k)=K(0.71429)=1.86282,式中θ=sin-lk=45°35',則可得出:
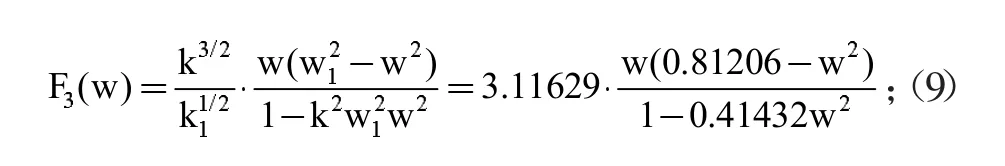
當(dāng)n=4(偶數(shù)),k=1/1.4=0.71429
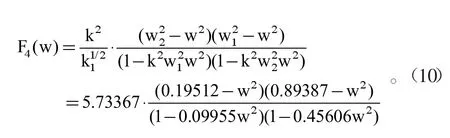
1.3 濾波器中橢圓函數(shù)的數(shù)學(xué)模型
橢圓函數(shù)的性質(zhì)應(yīng)用于濾波器,需要對(duì)其的數(shù)學(xué)模型進(jìn)行確定包括橢圓函數(shù)特征函數(shù)的相關(guān)參數(shù),物理上表現(xiàn)在濾波器上的性能為衰減特性、工作傳輸函數(shù),通過數(shù)學(xué)模型能夠把濾波器的電路圖和相關(guān)的電器元件參數(shù)進(jìn)行設(shè)計(jì)。
衰減特性為:
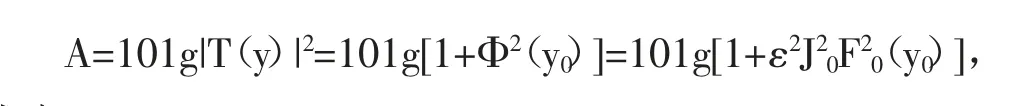
式中y0=ω/ω0。
這個(gè)衰減特性函數(shù)的特征函數(shù)為:
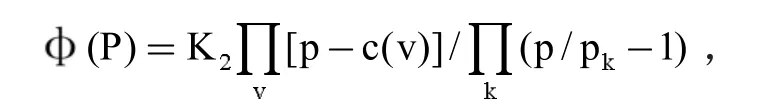
式中v=1,…,n;k=1,…,(n-1)/2,s作為復(fù)歸一頻率,有函數(shù)s=jy,s(v)為傳輸函數(shù)的自然模式,即傳輸函數(shù)的零點(diǎn);pk是衰減函數(shù)的衰減極點(diǎn),存在于阻帶的范圍內(nèi);c(v)是衰減函數(shù)的衰減零點(diǎn),存在于通帶的范圍內(nèi);n是電路階次。切比雪夫近似在數(shù)學(xué)上表現(xiàn)為過渡帶趨于∞時(shí),橢圓函數(shù)能夠獲得的數(shù)值,可以通過一系列的遞推公式獲得奇階橢圓函數(shù)近似。通常來說,能夠獲得兩個(gè)遞推公式,依照正向的遞推公式,能夠獲取切比雪夫近似的一般通式,同時(shí)在這基礎(chǔ)上能夠利用反向遞推的方法,獲得橢圓函數(shù)的相關(guān)模型,進(jìn)而可以獲得橢圓函數(shù)濾波器的電路形式和電路元件的相關(guān)數(shù)據(jù)。
公式(6)的變化中,能夠獲得特征函數(shù)為零的頻率點(diǎn),這些點(diǎn)對(duì)應(yīng)著傳輸函數(shù)的最大值:

這個(gè)函數(shù)當(dāng)中,如果n是一個(gè)奇數(shù),那么可以獲得:
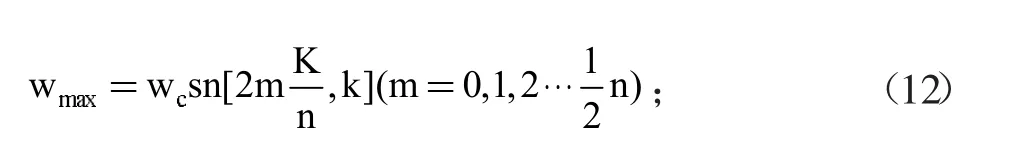
如果n是一個(gè)偶數(shù),那么可以獲得:
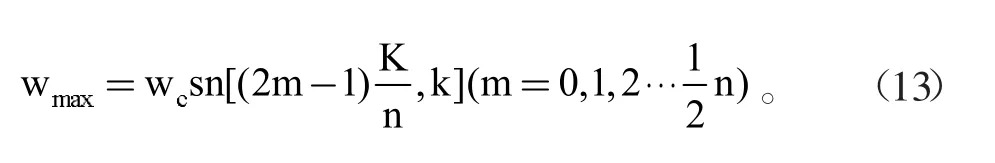
理論上能夠獲得的最小通帶增益為:
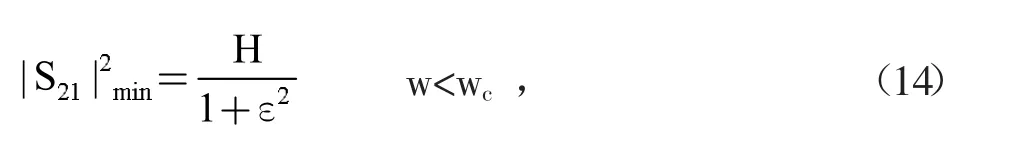
這個(gè)值對(duì)應(yīng)于Fn(w)=±1。
這個(gè)函數(shù)當(dāng)中,如果n是一個(gè)奇數(shù),那么可以獲得:
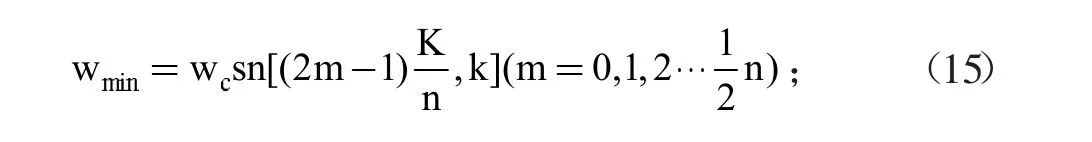
如果n是一個(gè)偶數(shù),那么可以獲得:
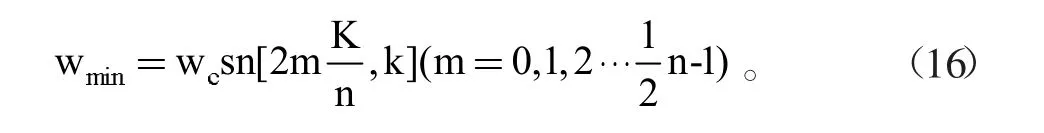
所以理論上可以獲得的直流增益是:

函數(shù)值的曲線上有一個(gè)極點(diǎn)(最低點(diǎn)),此時(shí)通帶上有w=wc,可以獲得對(duì)應(yīng)于n的最小增益都有:

H是一個(gè)固定值的情況下,ε(波紋因子)主要是通帶中峰表現(xiàn)。其中波紋和通帶的數(shù)學(xué)關(guān)系為:

阻帶能夠得到的最低點(diǎn)是零,為特征函數(shù)的極點(diǎn),因此:

所以理論上可以獲得的阻帶增益是:
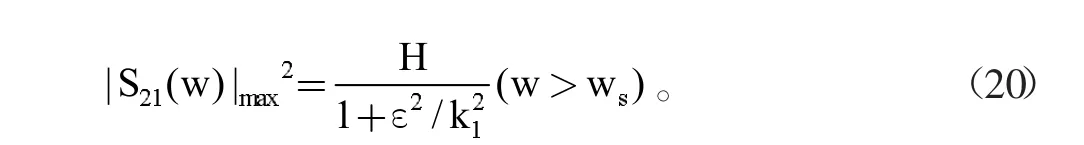
這時(shí)的頻率為:

阻帶衰減量與k1,ε的函數(shù)值之間有如下關(guān)系:

增益特性從通帶到阻帶單調(diào)地減小,一般會(huì)把阻帶邊緣對(duì)應(yīng)的增益下降到最大處頻率稱為ws。這就有如下關(guān)系式:
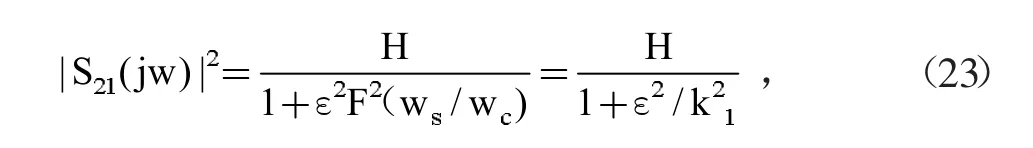
能夠獲得F為:

K為選擇因子,其倒數(shù)為陡度,表征過渡帶增益特性。
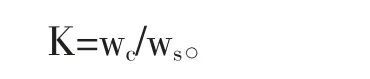
1.4 橢圓函數(shù)濾波器
橢圓函數(shù)為基礎(chǔ)的這一類濾波器具有有限傳輸點(diǎn),具有等波紋的特點(diǎn),定義傳輸函數(shù)為:
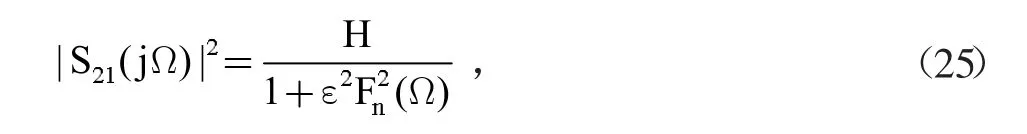
這個(gè)函數(shù)中,Ω為角頻率,通過第一類雅克比橢圓函數(shù)積分獲得,函數(shù)Fn(Ω)是關(guān)于Ω的函數(shù)。通過函數(shù)信號(hào)圖像的繪制,可以獲得橢圓函數(shù)濾波器的頻響曲線,見圖1。
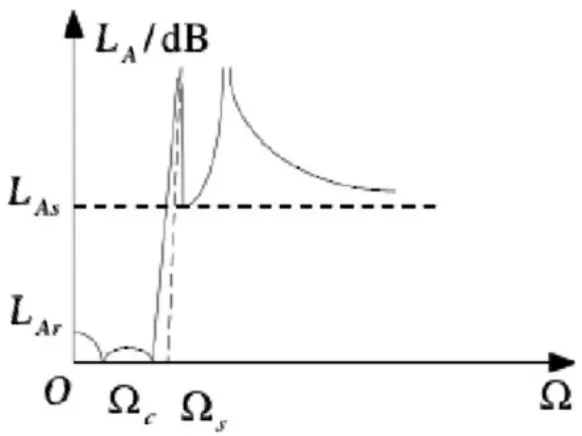
圖1 橢圓函數(shù)濾波器頻率響應(yīng)衰減特性
2 橢圓函數(shù)濾波器的應(yīng)用
通常微波濾波器有多種形式,濾波器的頻率響應(yīng)主要有巴特沃茲型、切比雪夫型和橢圓函數(shù)型。巴特沃茲型濾波器要需要更多的階數(shù),這就使得這種濾波器的設(shè)計(jì)更為復(fù)雜,而橢圓函數(shù)濾波器能夠使濾波器獲得更好的選擇性,相較于另一種切比雪夫型濾波器,設(shè)計(jì)結(jié)構(gòu)上更加簡單易行。橢圓函數(shù)濾波器在設(shè)計(jì)中,通常使得其組成中相關(guān)的諧振電容電感器件成對(duì)排布,因而相比較與另外兩種濾波器,橢圓函數(shù)濾波器的性能更加優(yōu)越。同時(shí)在設(shè)計(jì)過程中,能夠利用橢圓函數(shù)的元件選擇,對(duì)橢圓函數(shù)濾波器的性能進(jìn)行調(diào)節(jié),從而使得橢圓函數(shù)濾波器在寄生效應(yīng)方面具有更大優(yōu)勢(shì),能夠讓系統(tǒng)S參數(shù)曲線更加符合預(yù)期。
吳勝陽概括總結(jié)了橢圓函數(shù)低通濾波器的工作原理和設(shè)計(jì)方法,通過MATLAB的仿真,結(jié)合橢圓函數(shù)的設(shè)計(jì)步驟,給出了一個(gè)能夠在微帶線上的橢圓函數(shù)低通濾波器設(shè)計(jì)方案。賈曉斌等采用了一種新的歸一方法,該方法基于DDS,能夠利用EDA軟件對(duì)Muhisim2001進(jìn)行仿真,通過對(duì)橢圓函數(shù)濾波器的結(jié)構(gòu),物理參數(shù),電階數(shù)等方面進(jìn)行設(shè)計(jì),他的設(shè)計(jì)讓他獲得了具有一定的較快衰減特性,并且幅頻性能也具有一定的優(yōu)勢(shì)的160MHz的7階橢圓函數(shù)濾波器。他的設(shè)計(jì)方案能夠應(yīng)用于不同頻段、階數(shù)、類型的濾波器設(shè)計(jì)。李嬋娟等以橢圓函數(shù)低通濾波器為基礎(chǔ),設(shè)計(jì)了一款能夠克服以往濾波器結(jié)構(gòu)過大,渡帶衰減慢等問題的高低阻抗線微帶低通濾波器,主要是利用了橢圓函數(shù),設(shè)計(jì)給出了這種濾波器相關(guān)參數(shù)的理論計(jì)算方法,利用ADS和HFSS對(duì)濾波器的設(shè)計(jì)進(jìn)行了模擬優(yōu)化,并最終做出了實(shí)物,展開測(cè)試驗(yàn)證,獲得了較好的實(shí)驗(yàn)結(jié)果,證明了他的設(shè)計(jì)方案是有效的。董利芳基于傳統(tǒng)的高低阻抗線結(jié)構(gòu)濾波器,利用橢圓函數(shù)設(shè)計(jì)了低通濾波器,能夠應(yīng)用于微波平面電路,通過HFSS仿真模擬可以獲得,該濾波器的過渡帶較傳統(tǒng)濾波器更陡峭,同時(shí)也具有更加寬泛的頻域,并且在物理結(jié)構(gòu)上能夠減小使用材料,減小體積和結(jié)構(gòu)復(fù)雜性。
3 結(jié)論
橢圓函數(shù)濾波器具有更高的選擇性和更好的性能優(yōu)勢(shì),在設(shè)計(jì)中,通常其組成中相關(guān)的諧振電容電感器件成對(duì)排布,橢圓函數(shù)濾波器的性能更加優(yōu)越。同時(shí)在設(shè)計(jì)過程中,能夠利用橢圓函數(shù)的元件選擇,對(duì)橢圓函數(shù)濾波器的性能進(jìn)行調(diào)節(jié),從而使得橢圓函數(shù)濾波器在寄生效應(yīng)方面具有更大優(yōu)勢(shì),讓系統(tǒng)S參數(shù)曲線更加符合預(yù)期,并且以橢圓函數(shù)為基礎(chǔ)的這一類濾波器具有有限傳輸點(diǎn),等波紋特點(diǎn),因而能夠應(yīng)用于高性能濾波器。

