國內外規范梯度作用下鐵路高墩溫度效應研究

李 龐

（中鐵六局呼和浩特鐵路建設有限公司，內蒙古 呼和浩特 010050）

0 引言

截止 2020 年，全國鐵路營業里程達到 13.9 萬 km，其中，西部地區占比 40.3 %。而我國西部地區地域遼闊，地貌復雜，鐵路線路往往會跨越高山、溝谷等地形，高墩大跨橋梁因其跨越能力強，在西部地區得到了廣泛的應用。我國西部地區跨越的經度、緯度較大，海拔高度差顯著，導致該地區氣候復雜多變，溫度極值較大，尤其西北地區，年溫差多在 50 ℃ 以上，而高墩大跨橋梁的橋墩往往采用空心截面形式，空心墩內部具有氣密性，且墩身材料導熱性能差，當環境溫度變化時，墩壁會產生沿厚度方向的非線性溫差，從而產生溫度應力［1］。故研究鐵路空心高墩的橫向溫度梯度效應具有十分重要的意義。

在空心高墩的溫度效應研究方面，顧皓瑋等［2］根據實測數據和傳熱理論模擬了熱力學參數和邊界條件，提出了一種柱板式空心高墩溫度梯度分布模式；戴公連等［3］采用熱－力耦合的三維有限元模型研究了鐵路高墩在極值溫度下的變形；林國濤等對高墩的溫度效應進行了數值分析；劉亞敏［5］研究分析了空心高墩的溫度應力；陳賢俊等模擬了日照作用下的空心高墩溫度并進行了溫度效應分析。現有研究中對于空心高墩沿壁厚方向的溫度梯度模式研究較少，且各國規范中大多只給出了梁體的豎向溫度梯度。

基于上述現狀，本文選取西北地區某鐵路空心高墩作為研究對象，建立實體有限元模型，將各國規范中梁體的豎向溫度梯度加載至橋墩壁厚方向，對比分析各國規范溫度梯度作用下橋墩的溫度效應。

1 工程背景及有限元模型

以西北地區某鐵路矩形空心高墩作為研究對象，墩高 109 m，材料為 C 35，底部實心段高 2.5 m，頂部實心段高 1.5 m。

采用 MIDAS FEA 建立橋墩及 0 號塊實體有限元模型，借助放樣、布爾運算等功能建立實體并考慮內、外壁四周的圓形倒角，采用映射功能劃分網格，共 50 112 個六面體單元，52 618 個節點。將桿系模型中 0 號塊位置處的內力加載至實體模型中 0 號塊兩側模擬成橋階段的邊界。有限元模型如圖 1 所示。

圖1 有限元模型（單位：m）

2 各國規范中溫度梯度

2.1 中國鐵路規范

根據 TB10092－2017《鐵路橋涵混凝土結構設計規范》［7］，沿梁高方向的溫度梯度按圖 2 進行計算。

圖2 中國鐵路規范溫度梯度

其梯度按指數函數變化，α為沿豎向溫差曲線指數，正溫度梯度時取 5，負溫度梯度時按 10 考慮。

2.2 英國規范

英國 BS5400 規范中關于箱梁的豎向溫度梯度考慮了橋面鋪裝層的影響，按折線變化，且正、負溫度梯度的變化規律不同［8］，如圖 3 所示。

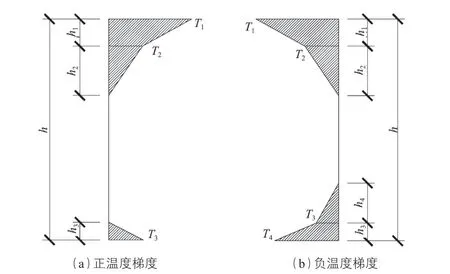
圖3 英國 BS 5400 規范溫度梯度

在空心墩溫度梯度效應計算時，由于空心墩內部封閉，不存在日照升溫現象，墩身溫度沿壁厚自外向內逐漸減小，將箱梁溫度梯度加載至橋墩時，可忽略梁體底部的溫度變化。正溫度梯度下取 T1 為 15.4 ℃，T2 取4.5 ℃；負溫度梯度下取 T1 為 -13.7 ℃，T2 取 -1 ℃。

2.3 美國規范

美國 AASHTO 規范中，將國土分為四部分，每一部分對應的溫差不同，但箱梁的正、負溫度梯度變化趨勢相同，且其分別對有、無瀝青覆蓋層做了溫差的修正［9］，如圖 4 所示。

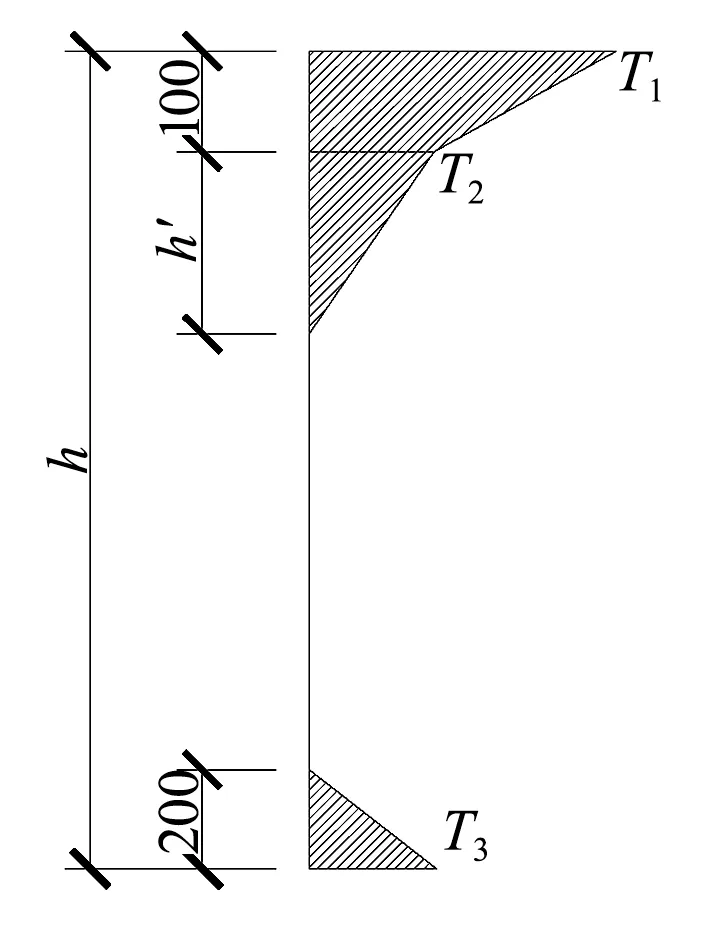
圖4 美國 AASHTO 規范溫度梯度（單位：mm）

將箱梁溫度梯度加載至橋墩時，可忽略梁體底部的溫度變化。正溫度梯度下取 T1 為 30 ℃，T2 取 7.8 ℃；負溫度梯度下取 T1 為 -15 ℃，T 2 取 -3.9 ℃。

2.4 德國規范

德國 DIN 101 將結構構件的溫度梯度分解為溫度常量、線性溫差和非線性溫度分布 3 個部分［10］，如圖 5 所示。在橋梁結構中計算溫差效應時，可忽略非線性溫度分布。

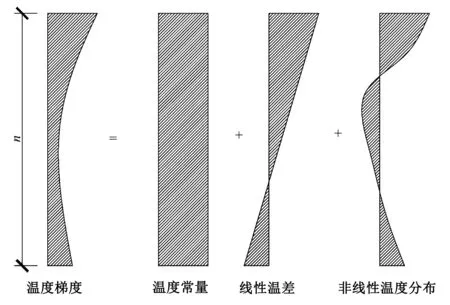
圖5 德國 DIN 101 規范溫度梯度

在空心墩溫度梯度效應計算時，其溫度梯度模式按規范中的混凝土板梁取值，正溫度梯度下取最大溫差為 22.5 ℃，負溫度梯度下取最大溫差為 -12 ℃。

2.5 新西蘭規范

新西蘭橋梁設計規范中，在距梁頂的 1.2 m 范圍內，其溫差按五次拋物線變化［11］，如圖 6 所示。

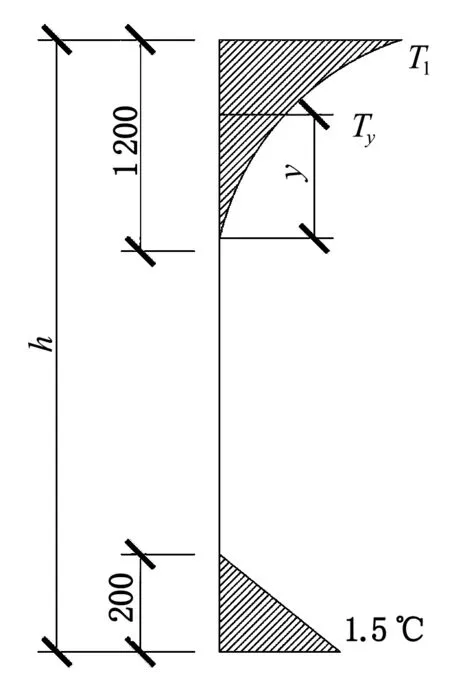
圖6 新西蘭橋梁設計規范溫度梯度（單位：mm）

將箱梁溫度梯度加載至橋墩時，可忽略梁體底部的溫度變化。正溫度梯度下最大溫差為 32 ℃，負溫度梯度下最大溫差為 -16 ℃。

3 溫度梯度效應計算結果

在正溫度梯度時，僅考慮單向日照作用，即橫橋向日照和順橋向日照，日照面與非日照面墩外壁溫度相差 10 ℃。順橋向日照時墩截面面積較大，在結果分析時僅給出順橋向日照作用下的正溫度梯度響應。

3.1 正溫度梯度

正溫度梯度下，各規范溫度梯度作用下橋墩內、外壁面位移規律基本一致，在此僅給出受陽光直射的外壁面沿墩高的位移曲線，如圖 7 所示。

圖7 正溫度梯度作用下橋墩位移

由圖 7 可知：①英國 BS5400 規范、美國AASHTO 規范、德國 DIN101 溫度梯度作用下，空心墩外壁位移基本一致，墩頂位移達到 21.4 mm；②新西蘭橋梁設計規范和中國鐵路橋梁規范溫度梯度作用下，墩身位移變化較平緩，墩頂位移分別為 8.7 mm 和 5 mm；③所有規范溫度梯度作用下，空心高墩底部均出現了不同程度的反向位移，英國 BS5400 規范溫度梯度作用下的反向位移達到了 1.1 mm，這是由于在有限元模擬時墩底截面所有節點均固結，在升溫作用下混凝土發生熱膨脹產生的位移無法向相鄰界面傳遞，導致墩底局部位置隆起。

正溫度梯度作用下向陽面橋墩外壁 von Mises 應力沿墩高分布曲線如圖 8 所示。

由圖 8 可知：①各國規范溫度梯度作用下，接近墩底墩高 1.5 m 處 von Mises 應力較大，最大可達 17.56 MPa，這是由于墩底完全固結導致的應力集中現象。②墩高自10～105 m，各規范作用下 von Mises 應力基本保持不變，其數值為“新西蘭規范＞中國規范＞美國規范≈德國規范＞英國規范”。為進一步探究各國規范溫度梯度作用下空心高墩的應力狀態，取 4 個特征截面（墩高 3、29、68、107.5 m，墩高由低至高依次編號為1-1～4-4）。各特征截面向陽側 von Mises 應力由外表面至內壁變化如圖 9 所示。

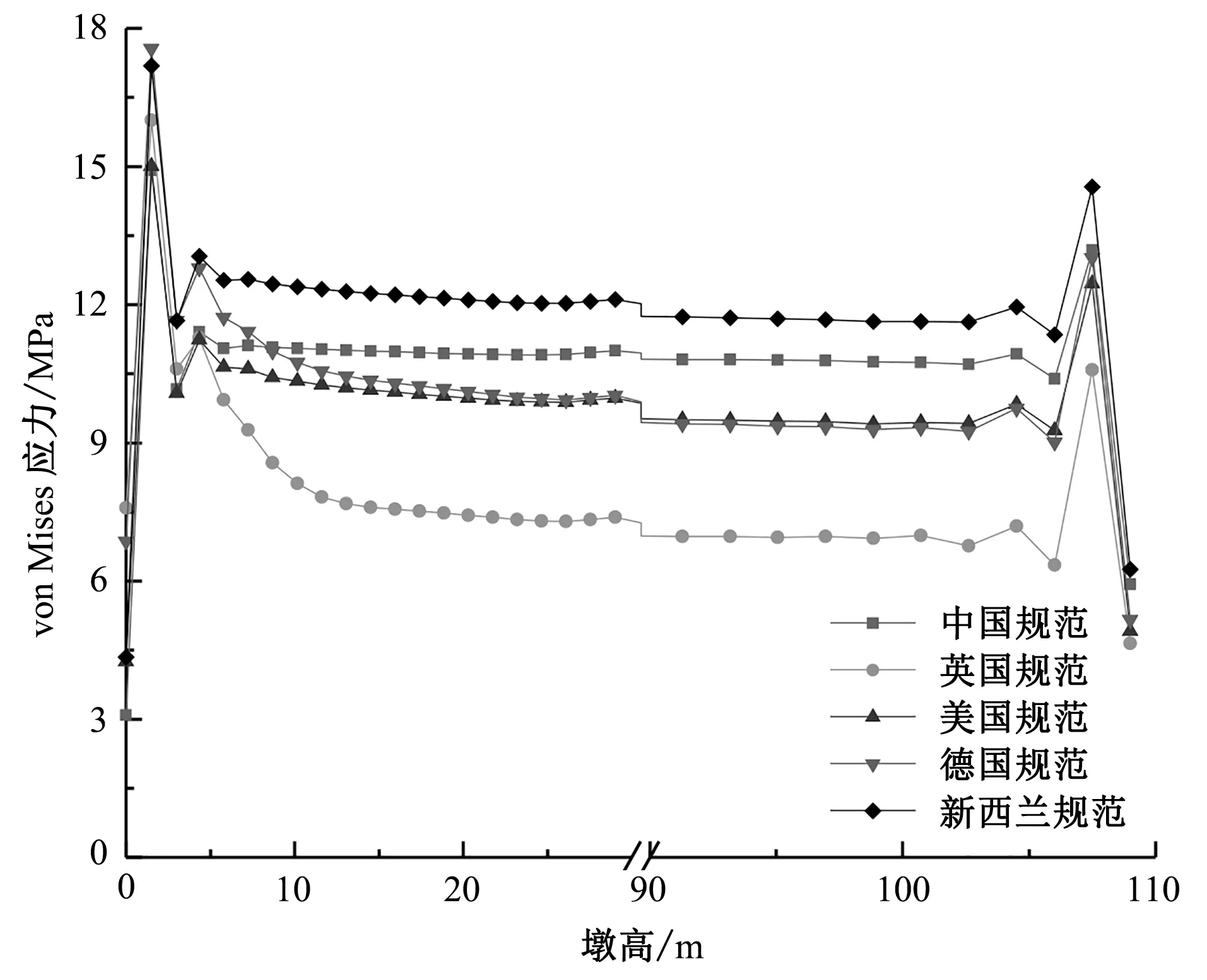
圖8 正溫度梯度作用下 von Mises 應力

由圖 9 可知：①各特征截面 von Mises 應力自外壁面至內壁面逐漸減小，至距外壁面 0.5 m 后趨于穩定；②墩高越高，各國規范溫度梯度作用下的 von Mises 應力趨于穩定后的值越接近，4-4 截面內壁面 von Mises 應力最大相差 0.71 MPa；③由圖 9（a）可知，墩底附近截面的內側 von Mises應力，其數值為“英國規范＞德國規范＞美國規范＞新西蘭規范＞中國規范”。

3.2 負溫度梯度

正、負溫度梯度作用下，von Mises應力沿墩高分布規律基本一致，在此僅給出負溫度梯度作用下各特征截面沿壁厚方向的應力曲線，如圖 10 所示。

由圖 10 可知：①各截面 von Mises 應力自外壁面至內壁面逐漸減小，1-1～3-3 截面在距外壁面 0.5 m 后趨于穩定，4-4 截面在距外壁面 0.5 m 后仍有一個較為緩和的減小趨勢；②墩高越高，各國規范溫度梯度作用下的 von Mises 應力在靠近內壁位置的值越接近；③由圖 9（a）可知，墩底附近截面的內側 von Mises 應力，其數值為“德國規范＞英國規范＞美國規范＞新西蘭規范＞中國規范”；④由圖 9（b）、（c）、（d）可以看出，各截面 von Mises 應力自外壁面至內壁面減小后，在距外壁面 0.3～0.5 m 范圍內有一個明顯的上升段，上升段最大差值 0.3 MPa。

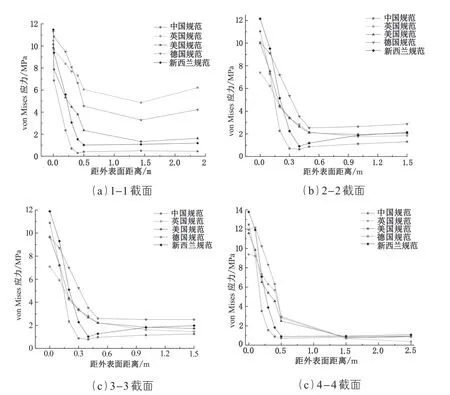
圖9 正溫度梯度作用下特征截面 von Mises 應力

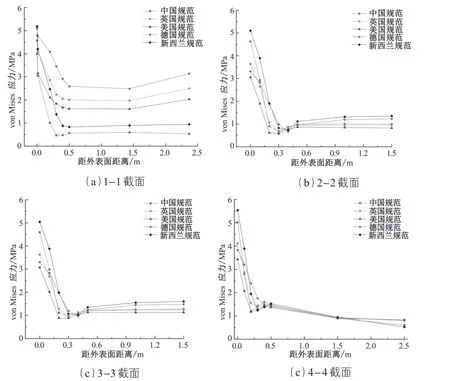
圖10 負溫度梯度作用下特征截面 von Mises 應力

4 結論

1）各國規范正溫度梯度作用下，墩身位移沿墩高逐漸增大，英國、美國、德國規范溫度梯度作用下的位移曲線基本一致，且墩頂位移較大，新西蘭規范次之，中國規范溫度梯度作用下的位移曲線增長最為平緩，墩頂位移也最小。

2）各國規范正、負溫度梯度作用下，von Mises 應力沿墩高變化趨勢相同，其數值為“新西蘭規范＞中國規范＞美國規范≈德國規范＞英國規范”，von Mises 應力沿壁厚均由外向內逐漸減小，達到一定距離后趨于穩定，且隨著截面高度的增加，達到穩定后各國規范溫度梯度作用下的應力值趨于一致。

3）墩底局部區域內，各國規范溫度梯度作用下的von Mises 應力值相差較大，正溫度梯度作用下英國規范最大，負溫度梯度作用下德國規范最大，正、負溫度梯度作用下中國規范的應力均最小。Q