底盤構件多軸隨機載荷下高周疲勞準則研究

董國疆 張 猛 魏留偉 張永強

1.河北省特種運載裝備重點實驗室(燕山大學)，秦皇島，0660042.先進鍛壓成形技術與科學教育部重點實驗室(燕山大學)，秦皇島，066004

0 引言

汽車零部件疲勞可靠性是評價汽車的重要指標之一[1]。對汽車底盤結構件而言，絕大多數疲勞失效發生在隨機載荷下[2]，而隨機載荷下的疲勞分析不同于恒幅載荷下的疲勞分析，隨機載荷下的零件會呈現多軸應力狀態。雖然關于構件多軸疲勞壽命預測已有較為深入的理論研究，但將這些理論應用在汽車構件壽命預測和分析的研究卻鮮有報道，主要原因有：疲勞失效發生的特定平面不易獲取，多軸疲勞加載下材料平面上的剪應力/應變幅值等參數值的確定方法研究較少[3]。為更準確地預測汽車零部件壽命，研究多軸疲勞準則在車輛領域的應用尤為重要。

國內外對零部件耐久性預測準則開展了諸多有益的研究。劉俊等[4]使用虛擬迭代的方法提取駕駛室懸置處和翻轉機構處的載荷譜，在nCode軟件中使用基于靜強度理論的等效應力/應變的方法進行壽命計算，與臺架強化試驗壽命相比，誤差在28.1%以內，該方法提取載荷準確，但未考慮多軸受力對疲勞壽命的影響。劉海燕等[5]通過對曲軸進行瞬態分析得到危險點應力信息，然后使用基于靜強度理論的von Mises等效應力與基于最大剪應力幅平面的McDiarmid準則計算曲軸疲勞損傷，通過對比得出McDiarmid準則從裂紋萌生和擴展的機理上來說更合理，該研究還介紹了隨機載荷下疲勞分析的流程，將最大剪應力幅平面的選取進行了簡化，但對大部分隨機載荷并不適用。錢立軍等[6]通過道路模擬試驗得到輪胎激勵，結合多體動力學模型得到下擺臂連接點載荷譜，使用Wang-Brown多軸疲勞模型對下擺臂進行疲勞分析，并與路試情況進行對比，仿真與實驗結果表明，下擺臂的最危險位置接近，且該位置處的疲勞壽命也十分接近。GAO等[7]對Zhang-Yao準則在頻域內重構并進行了多軸隨機壽命載荷下的壽命預測，通過與試件實驗結果對比可得預測結果大部分處于兩倍分散帶內，此外在計算最大剪應力幅平面時發現，在時域內使用最小外接圓法，在頻域內則要采用基于頻域的方法進行計算。KASHYZADEH等[8]、SHARIYAT[9]使用McDiarmid準則、Findley準則、Dang Van準則等多種高周疲勞準則計算轉向節與穩定桿在隨機載荷下的疲勞壽命，與實驗數據對比并從預測精度方面評估每種準則，但未明確說明隨機載荷下臨界平面的選取方法。

當前研究汽車零部件疲勞壽命側重于使用基于靜強度理論的等效應力/應變法，即使應用多軸疲勞準則也多是簡單載荷下的壽命計算。本文以轉向節為研究對象，使用基于靜強度理論的von Mises高周疲勞準則與基于臨界平面的C-S準則、McDiarmid準則等七種高周疲勞準則計算轉向節隨機載荷下的疲勞損傷，并分析臨界平面準則中基于的最大剪應力幅平面、最大損傷平面和第一主應力最大值平面三種臨界平面在隨機載荷下的計算方法，然后從等效應力幅分布、預測壽命、計算成本三個方面對準則進行分析評估。

不同高周疲勞準則以臨界點的應力狀態為計算的基礎數據，通過統計得到臨界點的幅值分布與壽命預測規律。雖然在相同路段下汽車不同底盤部件的應力幅范圍不同，但是應力分量之間的比例關系具有相似性。本研究以試驗場采集到的典型強化路載荷譜為原始數據，同時轉向節屬于典型的底盤部件，因此統計得到的規律對汽車底盤部件具有適用性。

1 多軸高周疲勞準則理論

目前使用廣泛的多軸高周疲勞準則包括von Mises準則、McDiarmid準則[10]、Dang Van準則[11]、Zhang-Yao準則[12]、Findley準則[13]、C-S準則[14]。

(1)von Mises準則。von Mises準則是目前對汽車零部件壽命預測應用最廣泛的準則，此準則要求計算點的各應力分量時間歷程為同頻率、零均值且無相差時計算結果才相對準確，其等效應力幅表達式為

(1)

其中，σa，von為von Mises準則等效正應力幅；Δσij(i，j=1，2，3)為各應力分量變程。應力幅為應力變程的一半，計算隨機載荷下疲勞壽命時通常用下式進行等效：

(2)

其中，σij(i，j=1，2，3)為各應力分量；Δ(·)表示計算整個等效應力時間歷程的變程函數，即首先計算等效應力時間歷程，再進行循環計數獲取等效應力幅。這樣雖然會使計算結果的準確性降低，但不需要計算與考慮各應力分量變程與相位差的影響，更加便于應用，所以被廣泛采用。

(2)Carpinteri-Spagnoli準則(C-S準則)。C-S準則為二維應力場下的von Mises準則的擴展形式，認為法向應力平均值會降低金屬材料的抗疲勞性能，所以需要對正應力幅進行平均應力修正。通過將多軸非比例應力轉化為單軸零均值應力進行損傷計算，其等效應力幅表達式為

(3)

其中，σa，C-S為C-S準則等效正應力幅；σaeq為經平均應力修正后的等效正應力幅；τa為剪應力幅；σ-1、τ-1分別為應力比R=σmin/σmax=-1時的拉伸和扭轉疲勞極限，σmin、σmax分別為循環載荷下的最小應力和最大應力；σm為正應力均值；σa為正應力幅；σu為強度極限。

(3)McDiarmid準則。目前McDiarmid準則在多軸疲勞方面的應用較多，它兼顧了便捷性與準確性，幾乎是一種單參數的臨界面準則，其等效應力幅表達式為

(4)

其中，τa，McD為McDiarmid準則等效剪應力幅；τ-1，AB為出現A型裂紋和B型裂紋對應的單軸純扭加載下的疲勞極限，A型裂紋沿著試件表面擴展，B型裂紋由試件表面向內部貫穿，對于拉-扭加載，一般發生A型裂紋[15]，有τ-1，AB=τ-1；σn，max為最大正應力。

(4)改進的McDiarmid準則。SHARIYAT[16]研究發現，當法向應力的階數遠高于剪應力的階數時，McDiarmid準則預測壽命會變得不準確，因此需對其進行改進，改進后的McDiarmid準則可表示為

(5)

其中，τa，McD_1為改進后的McDiarmid準則等效剪應力幅。

(5)Dang Van準則。Dang Van準則是一種雙參數準則，該準則在定義等效應力時考慮了靜水應力σH(σH=(σx+σy+σz)/3，σx、σy、σz為3個正應力分量)的影響，是依據剪應力幅和最大靜水應力而構造出的多軸高周疲勞破壞準則，可表示為

(6)

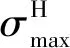
(6)Findley準則。Findley準則提出臨界平面內的正應力最大值與剪應力幅值可以作為疲勞評估的基本參量，該準則被認為比其他臨界面準則更加準確，其等效應力幅表達式為

(7)

其中，σa，Fin為Findley準則等效正應力幅。

(7)改進的Findley準則。SHARIYAT[16]改進了Findley準則，并通過對汽車某零部件進行試驗研究發現，改進后準則的壽命預測更加準確[19]，其表達式為

(8)

其中，τa，Fin_1為改進后的Findley準則等效剪應力幅；k為正應力在疲勞損傷中所占的比重。

(8)Zhang-Yao準則。Zhang-Yao準則以臨界面上最大剪切應力幅和最大法向應力的非線性組合為損傷控制參數，考慮了平均應力的影響，對臨界面上正應力與剪應力進行了平均應力修正，開展了多軸非比例加載實驗，對比結果表明該模型的預測準確性較好，其表達式為

(9)

其中，τa，Z-Y為Zhang-Yao準則等效剪應力幅。

在以上8種多軸疲勞準則中，McDiarmid、Dang Van、Findley等準則最初是用來校核零件是否滿足無限壽命的，而不是用于壽命估計，但通過對載荷時間歷程進行循環計數，結合損傷累計準則，這些準則越來越廣泛地應用于計算構件的疲勞壽命。

當前研究普遍認為剪應力的平均值對材料疲勞性能沒有影響，然而DAVOLI等[20]通過對某些材料進行實驗研究發現，當最大剪切應力低于剪切屈服強度時，平均剪切應力會明顯縮短疲勞壽命，并且計算累積損傷通常使用R=-1時的S-N曲線與T-N曲線，因此本研究考慮平均正應力與平均剪應力的影響，對上述準則中的正應力幅與剪應力幅均進行了平均應力修正。

2 強化路載荷采集與轉向節模態分析

2.1 試驗場載荷采集

實驗車輛為某品牌B級轎車，該車整備質量1538 kg，軸距2796 mm，前懸架為麥弗遜懸架，后懸架為多連桿懸架。根據試驗場耐久性試驗行駛規范，采樣頻率設定為1000 Hz，采集不同工況下的輪心六分力信號、輪心與車身加速度信號，在虛擬迭代過程中需要將輪心六分力作為迭代目標，將輪心與車身加速度作為監測信號。對實測信號進行去漂移、去毛刺、濾波、重采樣處理。本文重點采用典型隨機強化路石塊路乙(圖1)為研究對象，該路段對底盤零件形成的損傷較為明顯。

圖1 試驗場載荷譜采集Fig.1 Collection of load spectrum in test field

2.2 轉向節模態分析與驗證

在CATIA軟件中通過點云逆向的方式建立轉向節有限元模型，對轉向節受力與疲勞進行分析前需要進行自由模態分析與驗證，以確定所建立的模型是否符合使用要求。將模型導入HyperMesh軟件中進行3D網格劃分并檢查網格單元質量，模型材料的屬性見表1。對轉向節進行自由模態仿真，提取前6階固有頻率。如圖2所示，設計轉向節實體零件自由模態試驗，使用橡膠軟繩懸吊轉向節來模擬自由狀態。使用單點激勵多點響應的錘擊法測量轉向節模態參數，由于模態仿真得到的固有頻率不超過3200 Hz，因此為保證模態試驗能夠采集到最高階固有頻率，設置采樣頻率為10 kHz。由仿真與實測得到的前6階固有頻率(表2)可以看出，兩者的相對誤差不超過10%，所以轉向節有限元模型符合分析精度要求。

表1 轉向節材料屬性Tab.1 Material properties of knuckle

圖2 轉向節自由模態試驗Fig.2 Free modal test of steering knuckle

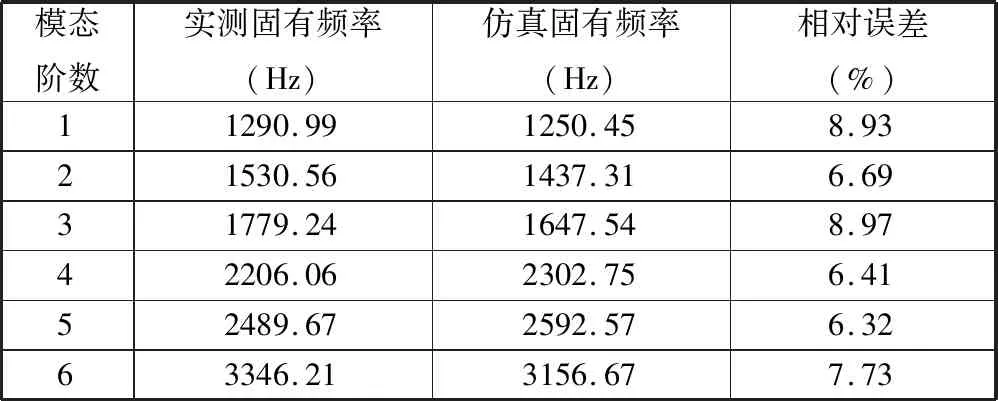
表2 轉向節自由模態固有頻率試驗與仿真對比Tab.2 Comparison of test and simulation free mode natural frequency of knuckle

3 轉向節特征點的載荷及應力分量提取

3.1 轉向節連接點載荷提取

在汽車行駛過程中，轉向節主要受到減振器、車輪中心、轉向橫拉桿和下擺臂傳遞來的力，對轉向節進行仿真分析時，需要將各連接點的力施加于有限元模型對應的節點上，連接點信息見圖3。由于試驗場只能采集到輪心受力，其他連接點的受力難以采集，因此需要使用虛擬迭代提取連接點載荷時間歷程。虛擬迭代法只需采集輪心載荷并將其作為車輛多體動力學模型輸入激勵，采集車身和懸架關鍵點作為監測信號，從而提取懸架零部件載荷譜[15]。虛擬迭代精度可由相對損傷和均方根值(RMS)相對誤差進行校驗，當相對損傷值在0.5～2之間或RMS相對誤差在20%以內時認為迭代精度滿足要求。本次整車輪心六分力(包括三方向力Fx、Fy、Fz以及三方向力矩Mx、My、Mz)迭代過程中的相對損傷值變化趨勢如圖4所示，可以看出，迭代至第6次時，六分力的相對損傷值均介于0.8022～1.1613之間。圖5為提取的石塊路乙路段下轉向節4個連接點共12條載荷時間長度為82 s的時域載荷曲線，對應位置與方向見圖3。

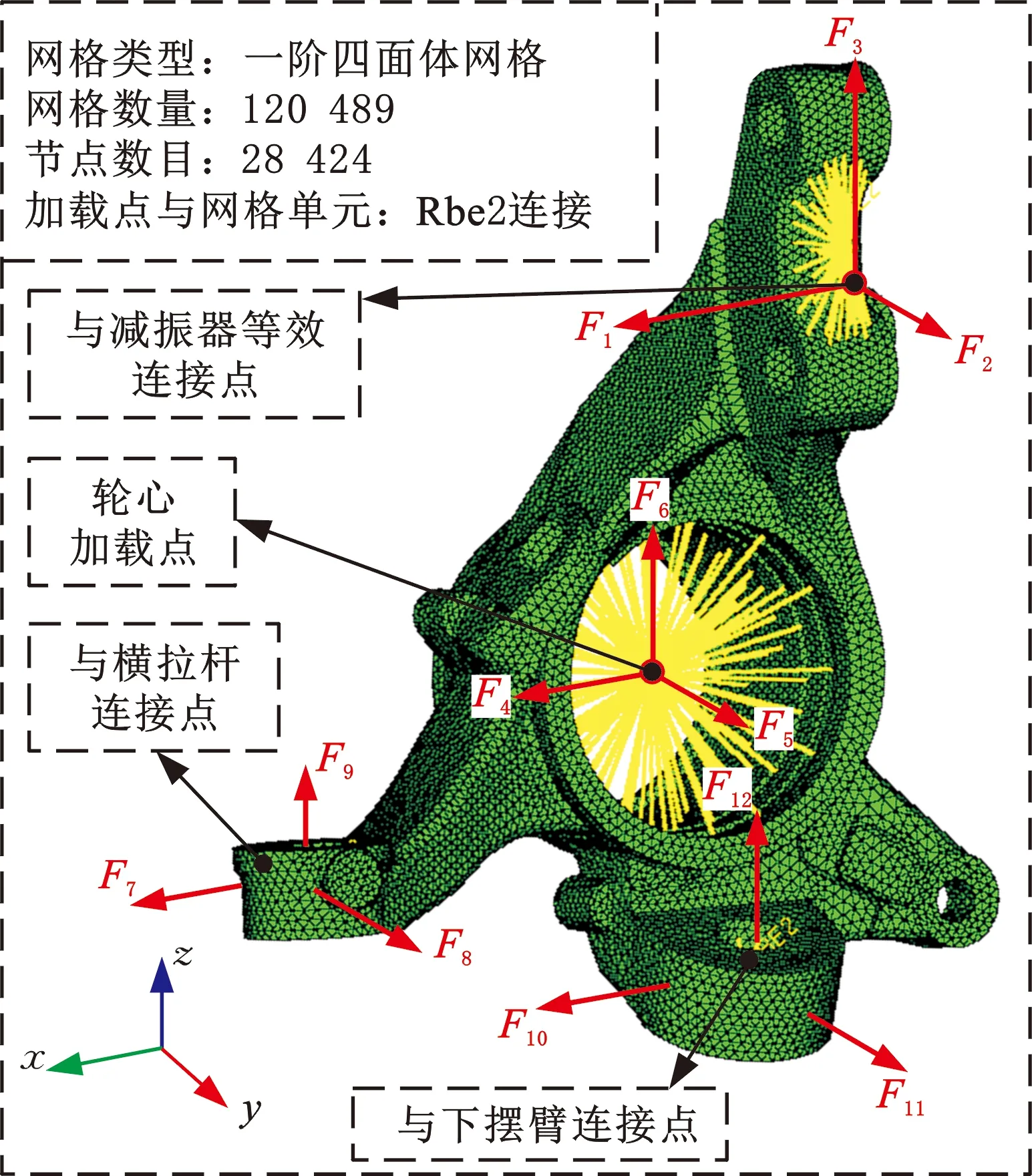
圖3 轉向節有限元及連接點信息Fig.3 Steering knuckle finite element and connecting point information

圖4 左前輪心六分力迭代相對損傷變化曲線Fig.4 Relative damage curves of six-component force iterative of left front wheel center

3.2 臨界點應力分量提取

轉向節的壽命取決于零件上最薄弱位置的耐疲勞破壞能力，所以首先需要找到疲勞熱點，然后分析其載荷循環次數進而判定零件壽命。在汽車行駛過程中轉向節各連接點承載狀況復雜，因此進行力學分析時引入慣性釋放法，即使用零件的慣性(質量)力來平衡外力。在Hypermesh軟件中對轉向節4個連接點分別在x、y、z三個方向上施加1 N的單位力，共12種載荷工況，進行慣性釋放分析后得到.op2文件。

疲勞熱點分析在nCode 13.0軟件中進行，導入.op2文件與12條時域載荷曲線(圖5)，并對模型賦予材料屬性，使用von Mises等效應力進行疲勞損傷分析。經分析可得到轉向節壽命值最小的節點(編號3731)位于圖6所示的危險區域。

(a)力F1 (b)力F2 (c)力F3 (d)力F4

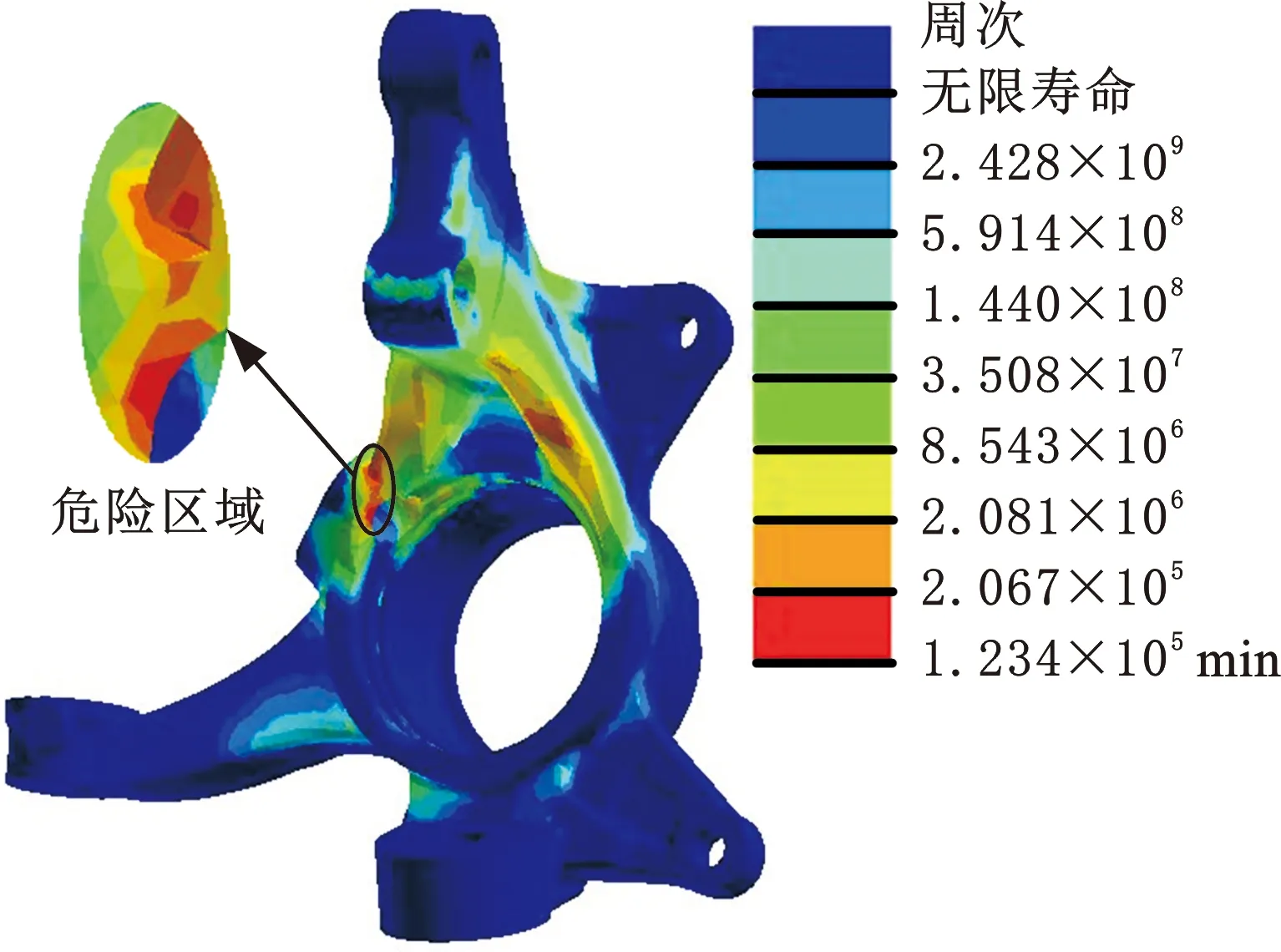
圖6 von Mises應力下疲勞仿真Fig.6 Fatigue simulation under von Mises stress

基于臨界面的損傷模型均需要提取臨界面上的正應力與剪應力，而正應力與剪應力需要根據壽命值最小節點處的應力分量計算得到。試驗車輛在石塊路乙路段行駛過程中，轉向節處于彈性變形內，且通過對輪心六分力進行頻譜分析可得頻率范圍均在50 Hz范圍內，遠小于模態試驗中第一階固有頻率1290.99 Hz，滿足這兩個條件即可使用準靜態法對轉向節進行動載仿真分析[21]。在ABAQUS軟件中對轉向節對應節點施加提取到的時域載荷譜并進行動載響應分析，最終可提取得到危險點處的6條應力分量曲線，見圖7。

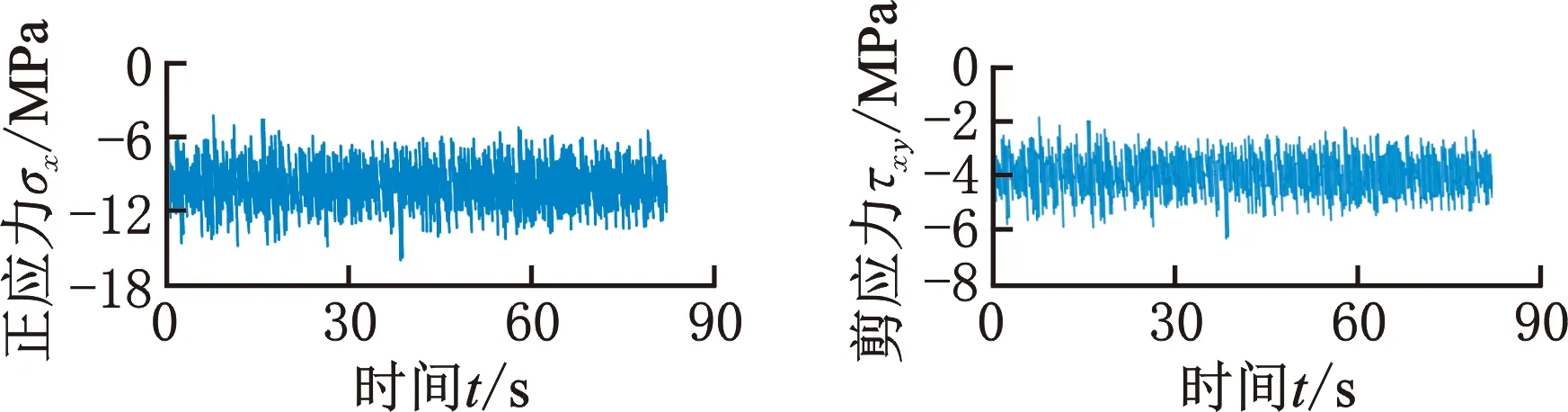
(a)正應力σx (b)剪應力τxy

4 臨界面選取與多軸循環計數

4.1 臨界面法簡介

臨界面法認為承載零件結構中某一給定損傷參數達到最大的平面往往是結構疲勞失效的平面，這個平面也常常出現裂紋的萌生和擴展。由于臨界面法評定結構疲勞壽命過程的物理意義更加明確，壽命預測結果更加準確，因此已得到了廣泛的應用[22]。如圖8所示，將承載零件某一節點的應力狀態在不同平面上分解，會得到不同的正應力與剪應力結果，平面方向由其法線方向的單位向量l=(sinθcosφ，sinθsinφ，cosθ)表示，其中θ為法線與z軸的夾角，φ為法線在Oxy平面的投影向量與x軸的夾角，且0°≤θ<180°，0°≤φ<180°，若O點的應力分量為

(10)

則此時正應力為

σ=lσijlT

(11)

全應力S沿坐標軸三個分量為

(Sx，Sy，Sz)=lσij

(12)

全應力與剪應力分別為

(13)

(14)

4.2 不同準則的臨界面選擇

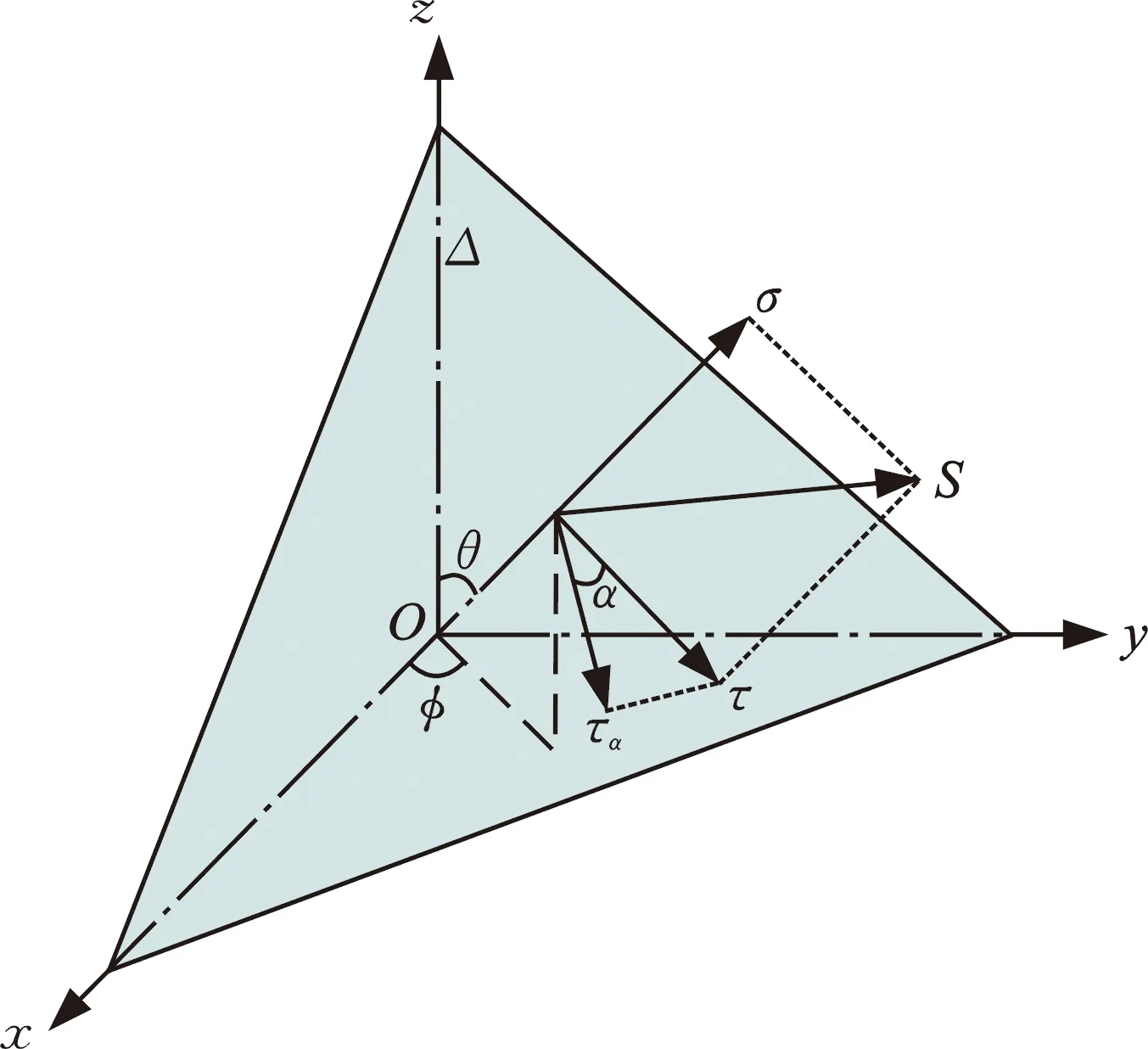
圖8 物體內某點受力示意圖Fig.8 Schematic diagram of a force on an object

不同疲勞準則對臨界面的定義不同，上述7種臨界平面高周疲勞準則所基于的臨界面主要有：最大剪應力幅平面(McDiarmid準則，改進McDiarmid準則，Dang Van準則，Zhang-Yao準則)；最大損傷的平面(Findley準則，改進Findley準則)；第一主應力最大的平面(C-S準則)。

4.2.1最大剪應力幅平面

在隨機載荷與比例載荷作用下，計算平面上剪應力幅值的方法不同。結構在承受多軸比例加載過程中，經過危險點O的任意平面時，正應力σ(t)與剪應力τ(t)僅大小發生變化，方向不會改變；而對于非比例載荷，正應力σ(t)方向仍然不會改變，僅大小發生變化，但剪應力τ(t)方向與大小均會隨時間不斷變化，其末端在平面上會形成一條軌跡線Ω，見圖9a。

多軸非比例載荷計算等效剪應力幅值的方法主要有最長投影法、最長弦法、最小外接圓法、最小外接橢圓法和最大方差法。前4種方法需要計算出具體的軌跡線Ω才能使用，由于隨機載荷非比例度較高，計算軌跡線Ω需要耗費大量時間，因此本文使用最大方差法計算等效剪應力幅。

最大方差法由SUSMEL[23]提出，以圖8中的平面Δ為研究對象，將所有時刻剪應力τ(t)沿偏離基準向量α角度(0°≤α<180°)的單位向量q方向分解得到τq(t)，見圖9b。其中，單位向量q經推導為

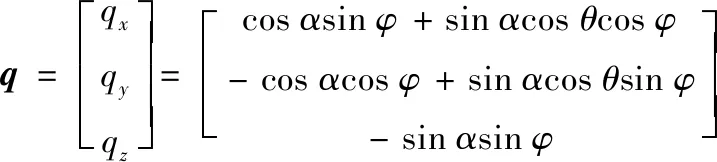
(15)

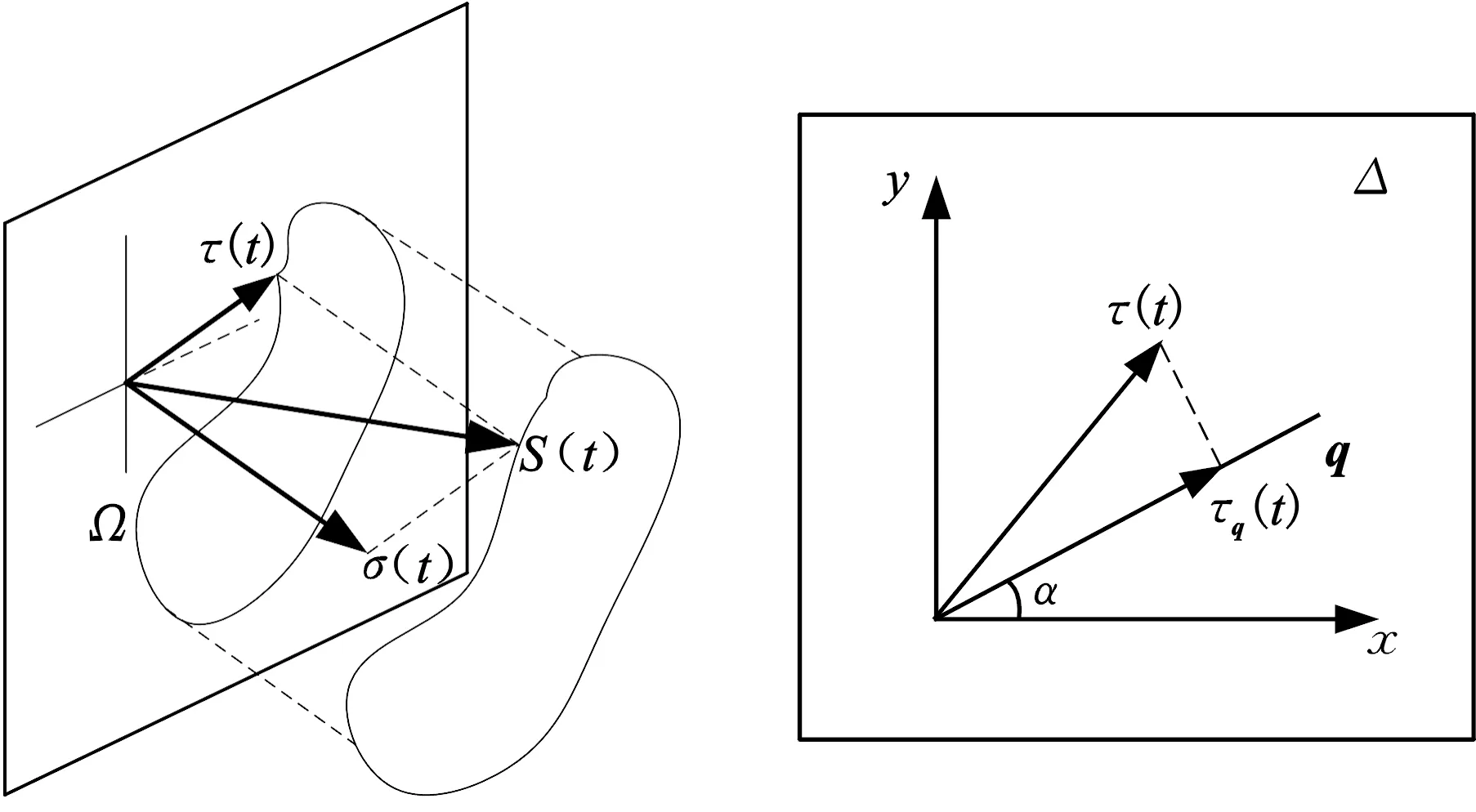
(a)臨界面剪應力軌跡線 (b)臨界面剪應力分解圖圖9 軌跡線與剪應力分解示意圖Fig.9 Track line and schematic diagram of shear stress decomposition

所有時刻沿q方向分解的剪應力為

τq(t)=qTσij(t)lT

(16)

沿q方向分解的剪應力方差Var(τq(t))經過形式變換后可表示為

Var(τq(t))=dTCd

(17)

式中，d為方向余弦向量；C為協方差矩陣。

等效剪應力幅可表示為

(18)

其中，max(·)表示函數最大值。由式(18)可知，剪應力方差達到最大的平面即為最大剪應力幅平面。本次計算過程中θ、φ、α均以5°的增量增大，共進行46 656次計算，得到θ=125°、φ=95°且α=100°時，Var(τq(t))達到最大值35.24 MPa，則最大剪應力幅平面的法線方向可表示為

l1=(-0.071，0.816，-0.574)

(19)

提取最大剪應力幅平面上的正應力時間歷程σ_1-t與剪應力時間歷程τ_1-t繪制于圖10。

(a)正應力 (b)剪應力圖10 最大剪應力幅平面正應力與剪應力時間歷程Fig.10 Normal stress and shear stress time history of maximum shear stress amplitude plane

4.2.2最大損傷的平面

Findley準則提出將剪應力幅與最大正應力的組合達到最大值的平面定義為臨界面，并在該平面上計算疲勞損傷。其中，剪應力幅可根據式(18)計算，而正應力僅大小變化，方向始終垂直于平面，因此可以使用常規方法計算幅值、均值等參數。在非比例載荷下，BOLCHOUN等[24]使用整個循環下的最大正應力值進行計算，且當應力比R=-1時有σn，max=σa；陳志超[25]利用Goodman公式對臨界面的正應力幅值進行修正，將所得到的對稱循環加載時的最大正應力幅作為最大正應力。本文在計算最大正應力時也采用上述方式進行求解，即先使用雨流計數法對平面上正應力時間歷程進行幅值與均值的統計，再通過Goodman平均應力修正法將均值修正為0，從而得到對稱循環加載時的最大正應力幅，Goodman平均應力修正法表達式為

(20)

其中，σa，-1為應力比為-1時的循環應力幅值。

計算過程中θ、φ、α均以5°的增量增大，共進行46 656次計算，得到θ=135°、φ=85°且α=95°時，τaeq+kσn，max達到最大值14.89 MPa，其中，正應力在疲勞損傷中所占的比重k可由式(8)計算得到。最大損傷平面的法線方向可表示為

l2=(0.062,0.704,-0.707)

(21)

提取最大損傷平面上的正應力時間歷程σ_2-t與剪應力時間歷程τ_2-t繪制于圖11。

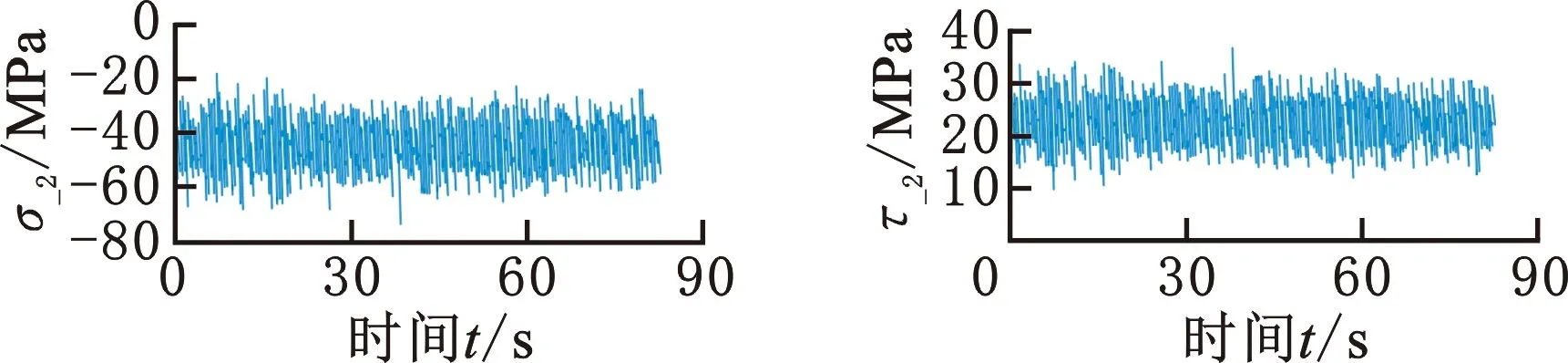
(a)正應力 (b)剪應力圖11 最大損傷平面上正應力與剪應力時間歷程Fig.11 Normal stress and shear stress time history of maximum damage plane

4.2.3第一主應力最大的平面

由于隨機載荷下的主應力方向不斷變化，文獻[26]提出通過權函數計算平均主應力方向，文獻[14]在此基礎上簡化了求解過程，提出平均主應力軸與對應第一主應力σ1達到最大值σ1max時刻的瞬時主方向重合，因此只需計算第一主應力達到最大值時刻對應的主平面。通過計算可得危險點第一主應力時間歷程，見圖12。提取第一主應力最大平面上的正應力時間歷程σ_3-t與剪應力時間歷程τ_3-t繪制于圖13。

圖12 危險點第一主應力時間歷程Fig.12 First principal stress at the point of danger

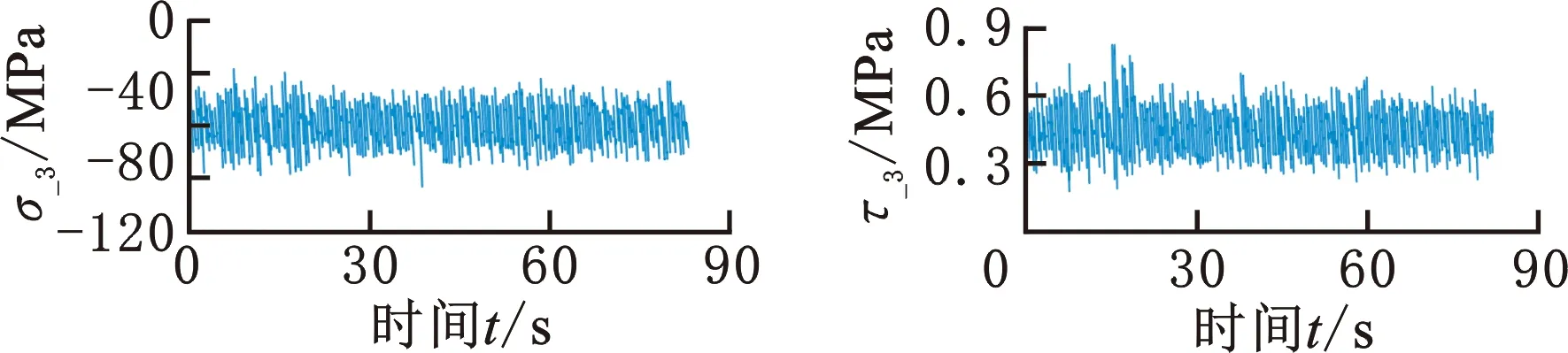
(a)正應力 (b)剪應力圖13 第一主應力最大平面上正應力與剪應力時間歷程Fig.13 Normal stress and shear stress time history of the first principal stress maximum plane

由圖12可以看出，當t=19.074 s時，第一主應力達到最大值94.314 MPa，此時θ=163.18°，φ=55.53°，則第一主應力最大值平面的法線方向可表示為

l3=(0.1638，0.2385，-0.9572)

(22)

4.3 多軸循環計數

循環計數是將復雜的載荷時間歷程簡化為具有循環概念的簡單載荷，目前普遍認可的計數方法是雨流計數，但該方法通常用來處理單軸隨機載荷與多軸比例載荷。對于多軸隨機載荷，臨界面上正應力與剪應力時間歷程有相位差、峰谷值不同時出現等復雜情況，因此相比單軸載荷的處理更為復雜。

有關多軸載荷循環計數方法的研究報道已經有許多。JORDAN等[27]在實驗中發現只有最大剪應變的一個半循環內的正應變變程對疲勞損傷是有效的，而另一個半循環內的正應變變程對疲勞損傷無貢獻，即不必區分加載半循環和卸載半循環。WANG等[28]認為對疲勞裂紋擴展有貢獻的有效正應變在兩個相鄰的最大切應變的轉點之間。

本文根據文獻[27]所提方法對臨界面上正應力與剪應力時間歷程進行雨流計數，舉例說明計數過程，如圖14所示。圖14是一段剪應力與正應力時間歷程曲線，以剪應力為主計數通道，提取到b-c-b′、f-g-f′、a-e-a′三個全循環。對于全循環b-c-b′，其變程為Δτ1，三個載荷信息點b、c、b′在正應力時間歷程中的對應點分別為2、3、4′。根據文獻[27]分別計算兩個半循環2、3與3、4′的變程，并選取最大值Δσ1作為輔通道的計數結果，最終可得到第一個多軸計數結果為(Δτ1，Δσ1)，同理可得到(Δτ2，Δσ2)、(Δτ3，Δσ3)。此外，使用這種方法對上述三種臨界面下提取的剪應力和正應力時間歷程分別進行多軸循環計數。

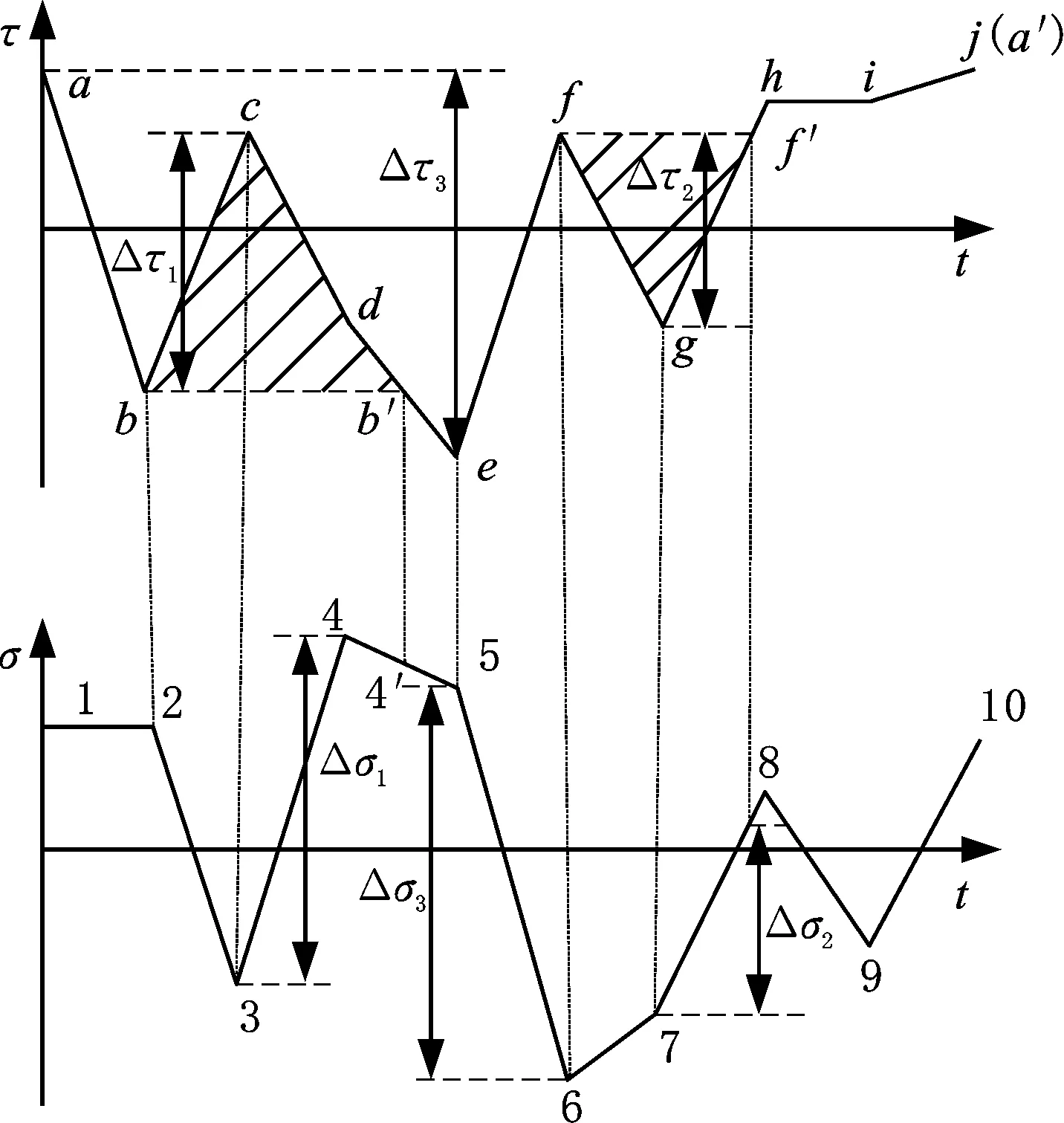
圖14 多軸循環計數示意圖Fig.14 Schematic diagram of multiaxis cycle count

5 多準則幅值分析及壽命預測

試驗車輛轉向節材料為QT400-15，抗拉強度σb=484 MPa，根據σ-1=0.4σbCDCSCLCR/Kf修正拉伸疲勞極限，通過查表[29]可得尺寸系數CD=0.89、表面質量系數CS=0.78、載荷系數CL=0.7、可靠性水平系數CR=0.753、疲勞缺口系數Kf=1.59，計算得到σ-1=44.55 MPa，對鋼鐵材料而言，超過107周次應力循環通常被認為無限壽命。為得到材料S-N曲線，還需要根據σ1000=0.9σbCR估算疲勞壽命為1000周次循環時對應的應力強度，得到σ1000=328.01 MPa。

材料的S-N曲線與T-N曲線通常用Basquin公式表示，其表達式分別為

(23)

(24)

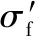
根據以上參數，計算得到S-N曲線為

σa，cri=1703.5(2Nf)-0.2167

(25)

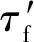
τa,cri=1081.8(2Nf)-0.2167

(26)

根據臨界面上正應力與剪應力的多軸雨流計數結果可計算每種準則下的等效應力幅，并統計每種準則等效應力幅的分布情況。通過以上數據計算修正后的拉伸疲勞極限與扭轉疲勞極限分別為σ-1=44.55 MPa，τ-1=28.29 MPa，其比值ξ=1.57。本次幅值統計分為小幅值[0，0.5σ-1(τ-1))、中等幅值[0.5σ-1(τ-1)，0.8σ-1(τ-1))、大幅值[0.8σ-1(τ-1)，∞)三個區間，具體如下：

小幅值

0≤σa，cri<22.28 MPa

0≤τa，cri<14.15 MPa

中等幅值

22.28 MPa≤σa,cri<35.64 MPa

14.15 MPa≤τa,cri<22.63 MPa

大幅值

σa,cri≥35.64 MPa

τa,cri≥22.63 MPa

記錄每個區間載荷循環次數繪制于表3。本文8種準則均是針對轉向節上同一節點的等效應力幅統計結果，統計得到的小幅值分布情況如下：McDiarmid準則占比最高達到78.4%，Zhang-Yao準則占比只有26.6%，Dang Van準則、Findley準則、改進Findley準則與改進McDiarmid準則占比接近。大幅值分布方面，Zhang-Yao準則占比最高達到59%，McDiarmid準則占比最小(僅為3.4%)。

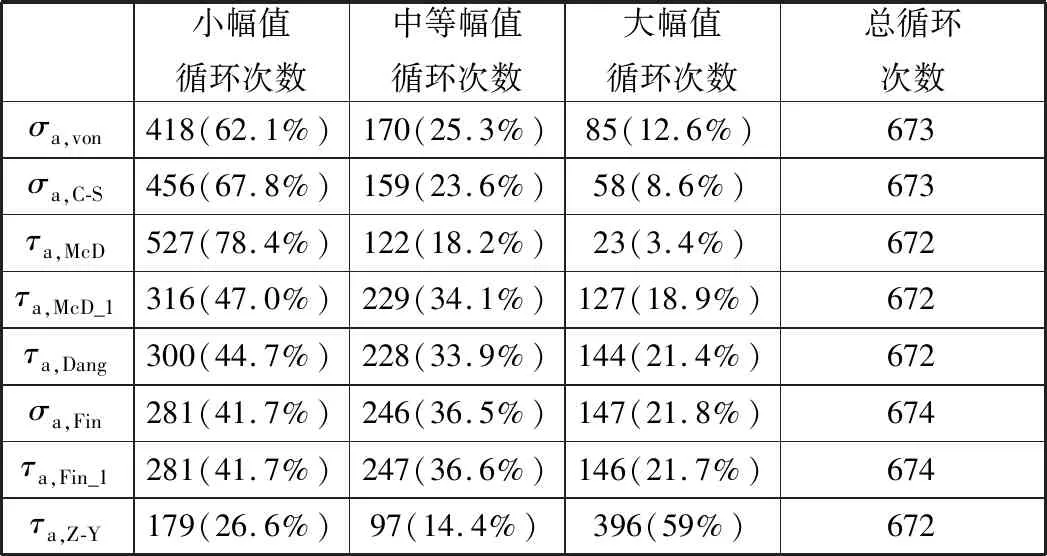
表3 各準則等效應力幅分布統計Tab.3 Statistics on the distribution of the equivalent forces of each criterion

只有等效應力幅大于疲勞極限才會產生損傷，統計每種準則下有效的等效應力幅列于表4，并使用Miner線性損傷累積理論計算危險點的總損傷與壽命。Miner準則因形式簡單、便于應用而被廣泛使用，其表達式為

(27)

式中，D為累積損傷；ni為i級載荷的循環次數；Ni為i級載荷下達到壽命時的循環次數；j為載荷級數。

表4為計算得到危險點在每種準則下的累計損傷與壽命結果，使用Dang Van準則、Zhang-Yao準則計算壽命最為保守，其次是von Mises準則、改進的McDiarmid準則、Findley準則、改進的Findley準則、C-S準則，McDiarmid準則的預測壽命值最大，明顯大于其他準則的預測壽命值。改進的McDiarmid準則與原準則相比，其預測壽命明顯縮短，而改進的Findley準則預測壽命與原準則預測壽命接近。

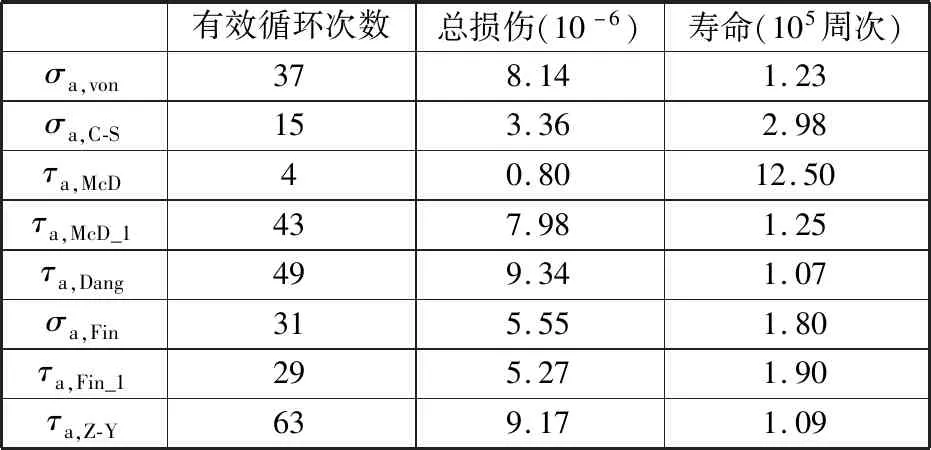
表4 各準則下轉向節損傷和壽命統計Tab.4 Statistics of the damage and life for the knuckle under each criterion

從計算成本方面考慮，每種準則的計算成本差異主要體現在提取臨界面環節。von Mises準則不需要多軸循環計數與求解臨界面，最便于應用；C-S準則使用第一主應力達到最大值時的應力分量便能計算臨界面方向；最大剪應力幅平面需要計算所有平面的剪應力數據，挑選出等效剪應力幅最大的平面；最大損傷平面(Findley準則)計算成本最高，需要計算所有平面的剪應力與正應力數據，使提取的平面剪應力幅與最大正應力線性組合最大。

6 結論

(1)對轉向節有限元模型進行了模態分析與驗證，對比前6階固有頻率的相對誤差均在10%以內，驗證了模型滿足仿真分析精度要求。將實車實測石塊路乙等試驗場強化路載荷譜作為疲勞分析的原始數據，并進行了轉向節連接點載荷譜分解。

(2)分析了隨機載荷下最大剪應力幅平面、最大損傷平面和第一主應力最大值平面三種類型臨界面的選取方法，并提取了臨界面上正應力和剪應力時間歷程；通過多軸循環計數，獲取到所有正應力幅與相對應的剪應力幅，并將多軸疲勞準則應用到隨機載荷下的壽命預測。

(3)從等效應力幅分布、壽命預測結果和計算成本等方面對各準則進行了分析評估。研究結果表明，Zhang-Yao準則的等效應力幅整體偏大，其預測壽命與Dang Van準則的預測壽命接近，但明顯短于其他準則的預測壽命，McDiarmid準則的大應力幅僅占3.4%，其預測壽命明顯長于其他準則的預測壽命，而改進的McDiarmid準則預測壽命明顯縮短，改進的Findley準則預測壽命與原準則預測壽命接近。von Mises準則計算成本低，最便于應用；Findley準則提取臨界面過程最復雜，計算成本最高。