一種基于最小二乘的航跡濾波方法
暢 言 魯 金 羅利強 任 倫 楊 璇
(西安電子工程研究所 西安 710100)
0 引言
雷達數據處理分系統上常采用α-β等方法進行航跡濾波。但是在特殊的情況下,如雷達測量雜波點較多或測量誤差大時,上述方法濾波結果并不一定非常理想,有時會出現航跡不連續,濾波精度差,航跡點跡誤關聯等問題。其原因是航跡濾波只考慮最新量測值和上一圈的濾波值,而對航跡歷史軌跡信息并未完全利用,最小二乘算法其原理是通過航跡若干個歷史關聯點跡和最新量測值進而空間擬合出一條最符合的曲線,其與真值誤差的平方和是最小的。在這種情況下最小二乘算法是有一定優勢的,采用歷史的關聯點跡數目可以根據不同的情況進行調整[1-2]。
1 方法原理
1.1 參數估計的概念
參數通常用來表示一個量,這個量可以是標量也可以是有值向量。而且按照參數是否是按時間變化可分為時常參數和時變參數[3]。對時常參數的估計稱為參數估計,設z(j)是在有隨機噪聲w(j)情況下獲得參數x的測量值,用函數形式可以表示為
z(j)=h[j,x,w(j)]j=1,2,…k
(1)
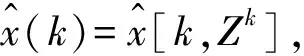
1.2 最小二乘估計

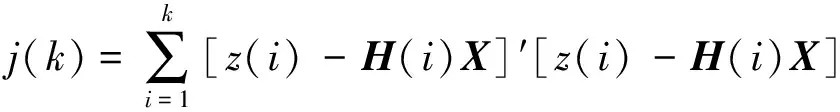
(2)
(3)
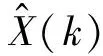
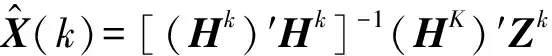
(4)
由于一般情況下,量測噪聲W(i)的協方差矩陣R(i)并不是同分布的,因此考慮使誤差的加權平方和
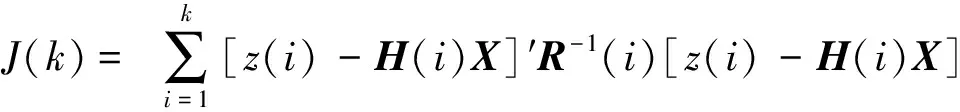
(5)
2 方法步驟
當航跡與雷達最新的量測點關聯成功后,開始選擇使用濾波點或量測點進行計算,確定使用的點跡數目,提取以前存儲的測量樣本或濾波點跡,如果歷史存儲的點跡數目小于確定的點數,則取所有歷史存儲的點跡信息,提取包括點跡的距離、方位、俯仰,相對時刻,次序等信息。將所有點跡,從雷達球坐標系(R,A,E)轉換到直角坐標系(X,Y,Z)下,然后分別計算X、Y、Z維的特征值,利用各維的歷史信息計算包括位置和,時間和,時間平方和,時間乘積和等特征值,然后計算出X軸、Y軸、Z軸初始時刻t0的位置估計值,然后根據初始值和時間間隔,計算最新量測點跡來到時刻的估計值,最后對計算出來的估計值和量測值進行加權平均得到濾波值,并轉換回球坐標系下進行輸出。
下面以工程上一階最小二乘算法為例,要使公式(6)成立
(6)
其中xl0,yl0,zl0為曲線初始各維濾波坐標,vx,vy,vz為各維上的濾波速度,ti為各維第n個點與第0個點的時間間隔,xi,yi,zi為各維第i個測量數據。
通過對式(6)xl0和vx求導后聯立,得出初始位置xl0和vx濾波速度,接著進行濾波,計算出當前x維濾波位置xln=xl0+vx·tn。
同理通過對yl0和vy求導,計算出yl0和vy最終得到yln,對zl0和vz求導,計算出zl0和vz最終得到zln,點數n可以根據不同的運動場景進行調整[7-12]。
3 實際應用
α-β算法是工程上常使用的一種算法,在直角坐標系下,根據上次的濾波結果,勻速外推并關聯上新的量測點跡后,將外推結果和新的量測點跡位置進行加權平均,形成新的濾波結果,速度也進行加權平均,α-β算法濾波系數根據具體情況不同,在0.55~0.8之間。
最小二乘濾波算法,采用是一階的五點的算法,即不考慮加速度,在直角坐標系下進行濾波,通過前五個量測點,對空間曲線進行擬合,使得五個量測點距離模擬曲線距離差平方和最小,計算出曲線的參數,并遞推到新來的量測點的時間,和當前最新量測位置加權計算出濾波結果。
實際中雷達做了二次檢飛試驗,第一次航跡效果圖如圖1所示,雷達工作模式為警戒模式,航跡中存在勻速直線運動、弱機動目標和強機動目標。為了對兩種算法進行對比,錄取數據后,每種方法重復回放100次,然后將濾波結果與真值進行分析與統計,結果如下。
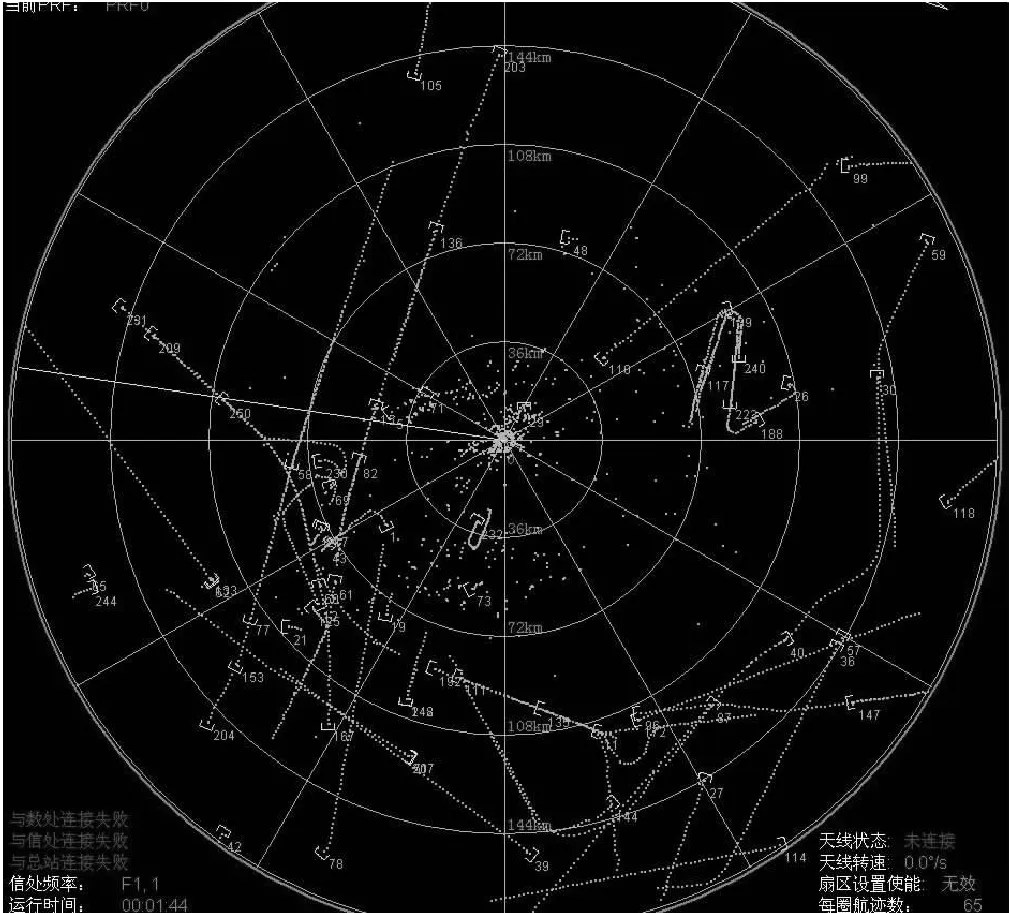
圖1 第一次檢飛試驗
數據處理濾波算法采用α-β算法,均方根誤差為距離34.2362m,方位0.1293°,俯仰0.1008°,數據處理采用最小二乘濾波法,均方根誤差為距離30.5044m,方位0.1161°,俯仰0.0989°。相比α-β算法,最小二乘法距離精度上提升了10.9%,方位精度上提升了10.2%,俯仰精度上提升了1.8%。
第二次檢飛試驗如圖2所示,雷達工作模式為目標指示模式,航跡中存在勻速直線運動和弱機動目標,分析結果如下。

圖2 第二次檢飛試驗
數據處理濾波算法采用α-β算法,均方根誤差為距離29.986m,方位0.1448°,俯仰0.067°,數據處理采用最小二乘濾波法,均方根誤差為距離26.2677m,方位0.1245°,俯仰0.0670°。相比α-β算法,最小二乘濾波距離精度上提升了12.4%,方位精度上提升了14%,俯仰精度上沒有變化。
由上述數據得知,最小二乘法是一種良好的航跡濾波方法,相比于傳統α-β算法濾波精度有所提升,并且工程中可以使用。
4 結束語
綜上所述,本文介紹了一種基于最小二乘的航跡濾波算法,通過空間擬合曲線去逼近真實的運動軌跡,由此進行濾波和外推,提高了航跡的精度,增加了終端航跡顯示的準確性,具有較高的工程應用價值。

