由八省聯考壓軸題引起的思考*
江蘇省揚州中學 (225009) 戚有建
一、考題展示
題目(2021年八省聯考卷22題)已知函數f(x)=ex-sinx-cosx,g(x)=ex+sinx+cosx.
(2)若g(x)≥2+ax,求實數a的值.
點評:本題是2021年八省聯考卷的22題壓軸題,選拔題,第(1)問考查函數不等式的證明,第(2)問考查不等式恒成立,考查分類討論、等價轉化、數形結合思想,有一定難度和區分度,本題結構簡潔、表達流暢、靜中有動、平中見奇、入口較寬,解法多樣,背景豐富,令人回味無窮,極具教學價值和研究價值.
二、常規解法
解析:(1)(分區間逐段研究)



綜上得,命題(1)得證.


圖1
(2)(先做必要條件,再驗證充分性)令h(x)=g(x)-ax-2=ex+sinx+cosx-ax-2﹐則h′(x)=ex+cosx-sinx-a,因為h(0)=0≥h(x),所以x=0是函數h(x)的極值點,所以h′(0)=0,即a=2,下面驗證充分性.此時,h(x)=ex+sinx+cosx-2x-2,h′(x)=ex+cosx-sinx-2,h″(x)=ex-sinx-cosx.
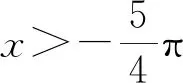

綜上得,a=2.
點評:對于第(2)小題,可以先做必要條件,再驗證充分性.關鍵是抓住h(0)=0≥h(x),如此則有x=0是函數h(x)的極值點,從而h′(0)=0,即a=2.
三、簡潔解法
解析:(1)(構建商函數,研究商函數最值)


綜上得,命題得證.

(2)(構建商函數,研究商函數最值)
令h(x)=g(x)-ax-2=ex+sinx+cosx-ax-2,則h′(x)=ex+cosx-sinx-a,因為h(0)=0≥h(x),所以x=0是函數h(x)的極值點,所以h′(0)=0,即a=2,下面驗證充分性.


四、命題背景
命題者是如何想到函數不等式ex+sinx+cosx≥2+ax的呢?研究后發現與泰勒公式有關.
五、背景應用
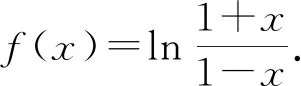
(1)求曲線y=f(x)在點(0,f(0))處的切線方程;
答案:(1)y=2x;(2)2.
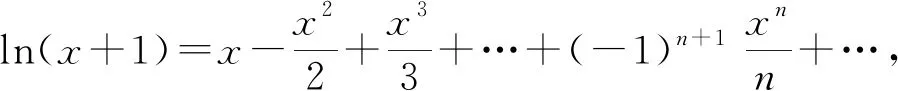
例2(2019年全國卷I文科21題)已知函數f(x)=2sinx-xcosx-x,f′(x)為f(x)的導數.
(1)證明:f′(x)在區間(0,π)存在唯一零點;
(2)若x∈[0,π]時,f(x)≥ax,求實數a的取值范圍.


