探求一類絕對值函數的最值問題
浙江省溫州育英國際實驗學校 (325036) 周立政
文[1]研究了一道含絕對值函數的最值問題,作者利用恒成立的條件取一個中間值并結合絕對值三角不等式得出結果.本文從絕對值的概念出發,結合函數圖象研究“中間值”的取法以及探討特殊值是否一定要包括區間端點、一定是取三個特殊點等問題,與同仁探討,請批評指正.
一、問題的引入
引例已知函數f(x)=x3,g(x)=|f(x)-ax-b|的定義域為[-1,2],記g(x)的最大值M,則M的最小值為( ).

為什么要選擇“g(-1),g(1),g(2)”?如果為了“好算”,似乎“g(-1),g(0),g(2)”更好算,但是選擇“g(-1),g(0),g(2)”會得出M≥0的結論.若取不到等號則這個算法找不到最小值.為什么要取三個特殊值?取兩個或者四個能得到結果嗎?
二、問題的提出與解決
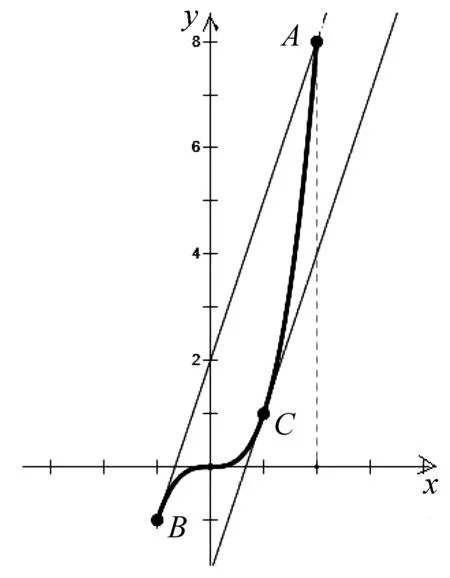
問題若函數y=|f(x)-(ax+b)|在x∈[m,n](m 分析:設M(a,b)=M,首先,|f(x)-(ax+b)|≤M恒成立,去絕對值可得-M≤f(x)-(ax+b)≤M,即-M+(ax+b)≤f(x)≤M+(ax+b), 所以,曲線段y=f(x)(x∈[m,n])被兩平行線l1:y=M+(ax+b)與l2:y=-M+(ax+b)“夾住”,它們正中間的直線是y=ax+b,如圖1, 圖1 圖2 引例解法2:(筷子方法)如圖3,作出函數y=x3(x∈[-1,2])的圖象,其中A(2,8),B(-1,-1),則直線AB的斜率kAB=3,作AB的平行線l并與曲線y=x3(x∈[-1,2])相切,易求切點C(1,1),直線AB與直線l的方程分別為y=3x+2,y=3x-2,所以M的最小值是 圖3 這就是解法1為何取f(-1),f(2),f(1)這三個數的原因:A,B,C三個點就是“筷子”與曲線段的“接觸點”,其中切點C的橫坐標就是解法1的中間量.上述解法是從“形”的角度得出結果的,從解題的嚴密性和簡潔性考慮,可采用解法1的書寫方法. 下面再舉幾例. 圖4 評注:本例中,采用的是曲線段的兩個端點和內部一個切點,共三個點. 例2 設函數f(x)=x2-ax(a∈R),x∈[0,1],|f(x)|的最大值為M(a),求M(a)的最小值. 圖5 評注:本例中采用的是曲線段的一個端點和內部一個切點,另一個端點不用,共兩個點. 圖6 評注:本例中,采用的是曲線段的兩個端點和內部兩個切點,共四個點. 如果修改題目條件a>0為a≤0,那么夾曲線的筷子距離最小的狀態是一根過A,另一根過B,且都平行于x軸,M(a,b)的最小值是1,此時a=0,b=0. 《普通高中數學課程標準解讀(實驗)》指出:“我們不但要繼續強調數學基礎知識和基本技能的學習,而且還要賦予基礎知識和基本技能新內涵,要始終重視對數學基礎知識和基本技能價值的深入剖析,以及加強對其發展性的足夠認識”.故此,我們要善于抓住絕對值和函數最值等核心知識,追根溯源,從不同角度觀察、比較、抽象并感悟數學思想方法,提升探究“所以然”的能力,真正把數學核心素養的教學落到實處.









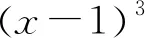
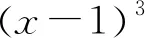


三、結束語

