風電接入對電力系統小干擾穩定影響分析方法

姜惠蘭，白玉苓，王紹輝，肖 瑞

（智能電網教育部重點實驗室（天津大學），天津 300072）

風力發電作為解決當前環境惡化和能源問題的重要途徑，在世界范圍內迅速發展，但風電并網會對系統的小干擾穩定造成很大影響，因此有必要研究風電場接入對系統的小干擾穩定的影響[1-2]。

目前國內外學者在此方面已取得一定的成果。常用的分析電力系統小干擾穩定性方法是阻尼轉矩法和特征根分析法。阻尼轉矩分析方法推導較復雜，常用于分析單機無窮大系統。故對于多機電力系統普遍采用特征根分析法。

文獻[3-9]利用特征根分析法研究雙饋風機DFIG（doubly-fed induction generator）接入對系統小干擾的影響。文獻[3]建立了風機的小干擾數學模型，仿真結果表明系統中引入了與風電場強相關的振蕩模式，且風電比例增加降低對外網阻尼特性。文獻[4]推導了含風電場的電力系統小干擾穩定的狀態矩陣，并通過算例仿真發現風電接入不參與系統原有的機電振蕩模式。文獻[5]利用四機兩區域系統仿真研究了風電出力、調度方式及機端電壓控制參數對系統小干擾穩定的影響。文獻[6]通過四機兩區域系統仿真研究了調速器、DFIG電阻及不同工況下DFIG和系統的動態交互行為。文獻[7-8]主要研究了風電滲透率的變化對系統小干擾穩定的影響。文獻[7]研究了DFIG工作在不同風速運行模式下，電力系統振蕩的模態和阻尼隨風電滲透率的變化情況。文獻[8]通過算例仿真表明當風電滲透率增加到50%以上時會對系統的阻尼產生負面影響。但上述文獻大多是通過建立包括DFIG在內的全系統小干擾穩定模型，然后針對具體算例分析包含風電的系統小干擾穩定性，并沒有考慮到DFIG特殊的機電解耦特性，不能從理論上說明DFIG和系統的關聯關系，同時系統狀態矩陣的維數較大，容易造成維數災問題。文獻[9]建立了DFIG與1臺同步電動機相連的簡化系統，研究表明DFIG接入系統是通過改變系統穩定平衡點來影響其小干擾穩定性，但沒有從風電場的實際接入位置入手，所得結論的普適性有待商榷。

本文通過風電場接入后對系統節點電壓方程的修正和收縮處理，將風電場接入系統的位置信息和輸出特性反映到系統同步機之間的電氣聯系中，使風電場對系統的影響量化為對同步機電磁功率的改變，并將其映射到系統狀態矩陣的改變，進而將風機接入與系統的小干擾穩定性聯系起來。采用這種方式可以更為直觀地反映DFIG與系統的關聯關系，降低了分析整個系統狀態矩陣的復雜性，為風電場接入對系統小干擾穩定性影響的量化分析提供了途徑。

1 DFIG影響系統功角穩定性的途徑

電力系統的小干擾穩定性是指當系統受到小的擾動后，不發生自發振蕩或者非周期性失步，能自動恢復到起始運行狀態的能力。對于傳統的機電暫態過程，當系統遭受擾動后，同步機的電磁功率受到影響，并通過“電磁功率-功角”特性影響各同步機的功角，從而引發同步機轉子角振蕩，出現同步機功角的互同步穩定問題。但由于DFIG具有雙變流器結構與矢量控制，其輸出的電磁功率和自身的轉子運動特性沒有必然聯系[10]，所以DFIG主要是通過輸出功率特性影響同步機的運行特性，進而影響系統的小干擾穩定性。

小干擾穩定的研究目標是系統的同步穩定性，而DFIG的機械運動和功率特性沒有必然聯系，所以DFIG自身的轉子運動不是同步穩定性研究的部分，可將DFIG作為1個非自治因素，研究其向系統輸入的有功和無功功率。為分析方便，本文將DFIG的輸出功率特性用等效接地導納模型來代替，即

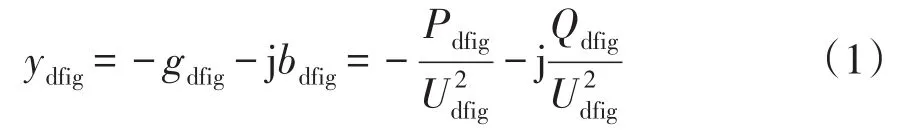
式中：Pdfig和Qdfig分別為DFIG輸出的有功功率和無功功率；Udfig為并網點電壓。

2 不含風電場時系統的狀態方程

設發電機組均為經典二階模型，發電機暫態電抗Xd′后的暫態電動勢E′及機械功率Pm均恒定，考慮系統經受小擾動，多機系統轉子運動方程在工作點附近線性化，可得到如下矩陣形式的增量方程：

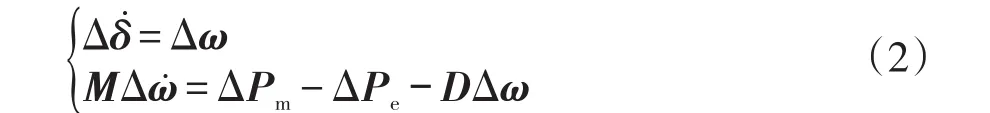
本文通過理論推導風電輸出功率與系統各同步機電磁功率的關聯關系，使風機接入對系統自身的小干擾穩定性的影響分析得以量化。

3 DFIG接入對同步機電磁功率的影響

將系統中的所有節點分為3類：發電機的內電勢節點S、DFIG并網節點W、其余普通功率交換節點R。由于發電機的電磁功率表達式與系統的網絡參數、各發電機的內電勢電壓和功角有關，需要對系統節點電壓方程等效變換，將系統各節點收縮至發電機內電勢節點。根據節點分類得到系統節點電壓方程，即

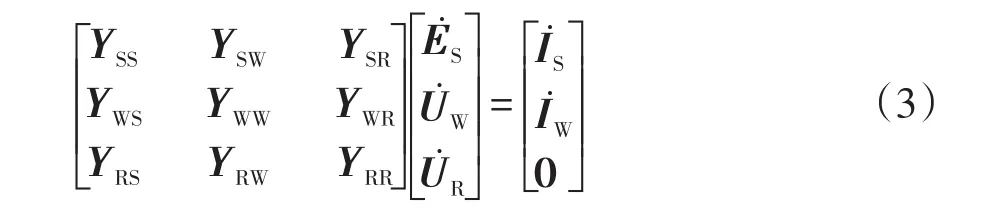
式中：YSS、YWW、YRR分別為節點S、節點W、節點R的自導納；YWS、YSW分別為節點W和節點S之間的互導納；YSR、YRS分別為節點S和節點R之間的互導納；YRW、YWR分別為節點R和節點W之間的互導納；?S為同步機內電勢；?W為DFIG并網節點電壓；?R為普通節點電壓；?W為DFIG并網節點注入電流；?S為同步機節點注入電流。

通過收縮普通節點R，得到同步機內電勢節點和DFIG并網節點的電氣聯系，即

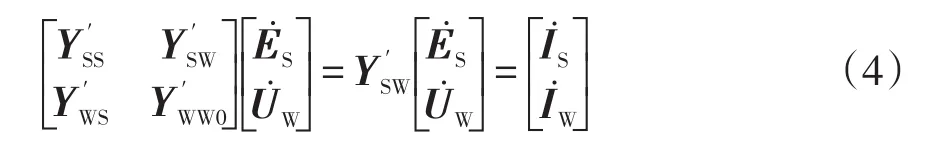
其中

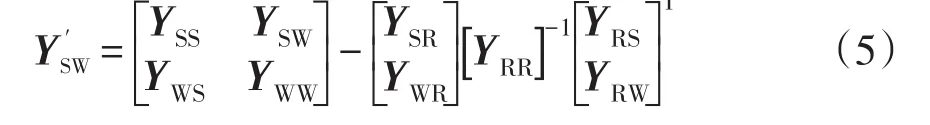
式中，Y′WW0為收縮節點R后節點W的自導納。

DFIG并網點W處用等效導納表示后，需要修正式（4）。由于W節點不再具備功率源特性，故W節點的注入電流?W應為0。DFIG等效接地導納影響了W節點的自導納，故Y′WW0應修正為Y′WW=Y′WW0+ydfig，即

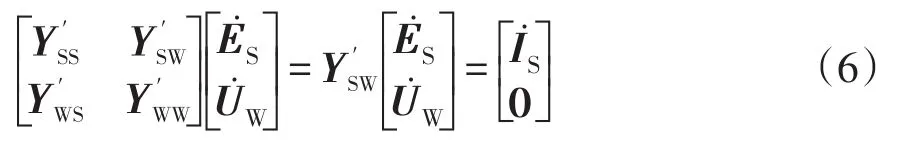
對式（6）進行進一步收縮可得

其中

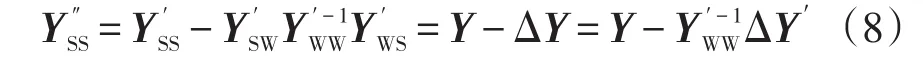
式中，Y和ΔY分別表示僅含有同步機系統收縮后的節點導納矩陣和DFIG接入后的修正量。

令

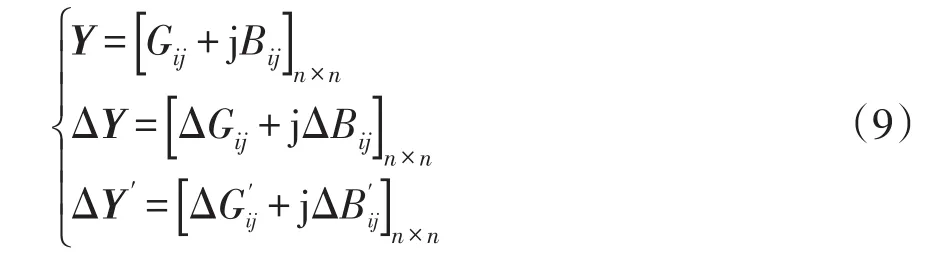
式中：Gij、Bij分別為僅含有同步機系統收縮后的同步機之間的電導、電納；ΔGij、ΔBij分別為DFIG接入后系統同步機之間電導、電納的改變量；ΔG′ij、ΔB′ij分別為DFIG接入后系統除去節點W自導納的同步機之間電導、電納的改變量。

這樣可將DFIG輸出功率信息轉移到對同步機間電氣距離的影響上，從而計算得到同步機i電磁功率 Pei，即

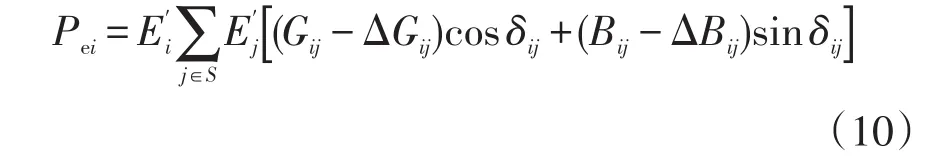
式中：E′i為第i臺同步機內電勢；δij為同步機i、j之間的相對角，δij=δi-δj，其中 δi為第i臺同步機的功角；S為節點S的集合。

4 含DFIG時系統的小干擾穩定特性

為了簡化說明，本文以圖1所示的含DFIG的兩機系統為例進行分析。從DFIG的實際接入位置入手，利用第3節的收縮方法求出DFIG接入系統后對各臺同步機電磁功率的量化影響，進一步將這種影響映射到DFIG對系統小干擾穩定的影響。

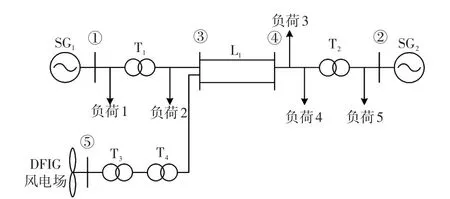
圖1 含DFIG的兩機系統Fig.1 Two-machine system with DFIG

從功率特性方面來看，DFIG的接入改變了同步機的自導納和互導納，由式（10）可知，同步機的電磁功率特性發生變化，即圖2所示的兩機系統功角特性曲線中的虛線變為實線，電磁功率特性曲線和機械功率特性曲線的交點為同步機1、2的相對功角初值δ120，所以δ120的相對位置發生了變化，即系統平衡點的位置發生了變化。相對功角穩態初值為

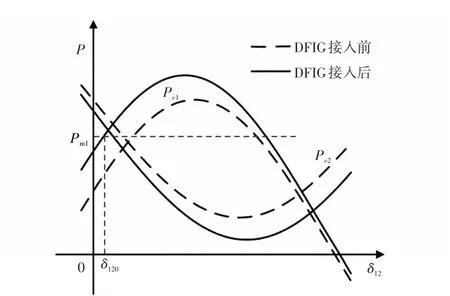
圖2 兩機系統的功角特性曲線Fig.2 Power-angle curves of two-machine system

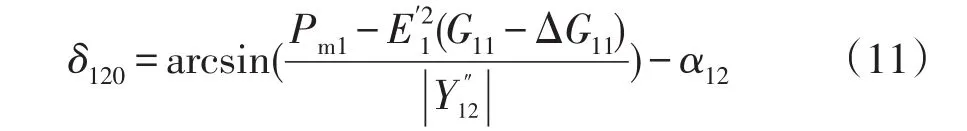
式中：α12為收縮后同步機1、2之間的互阻抗Y″12的阻抗角；Pm1為同步機1的機械功率。

由于同步機1、2的暫態電動勢恒定，取E′1=E′2=1，因在擾動過程中風電的有功影響遠大于無功影響[11]，下面推導中僅考慮DFIG有功輸出，即ydfig=-Pdfig/U2dfig。為表述方便，令Y′WW=(G0+ydfig+jB0)，對式（10）在平衡點處進行線性化，即

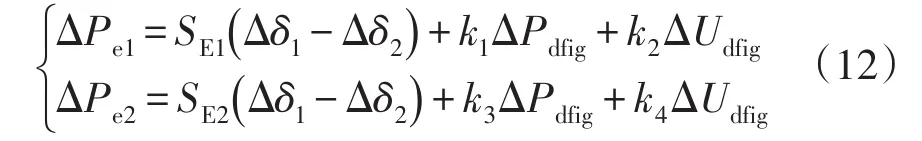
其中

式中：SE1和SE2分別為同步機1、2的同步轉矩系數；下標0表示平衡點初值；1、2分別為同步機1、2的功角增量。

根據文獻[11]，由有功功率微變引起的電壓微變較小，可忽略不計，即ΔUdfig=0，而DFIG輸出的有功功率變化量可以表示為dfig=gB，其中g為DFIG的動態頻率特性模值，B為DFIG并網點的頻率變化量。送電側和受電側的頻率微變均可用相應側的發電機轉速表示。以DFIG接入送電側為例，B=α11，α1為正系數，1為同步機1的轉速增量，設dfig=gα11=β11，式（12）可簡化為

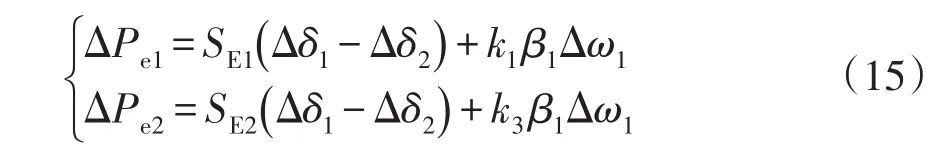
式中，β1為系數，β1=gα1。

式（15）表明DFIG的接入主要是從兩個方面影響系統的小干擾穩定性：①DFIG接入改變了系統的平衡點及各同步機之間的電氣聯系，主要影響了同步機的同步轉矩系數SE1和SE2；②系統發生小擾動的動態過程中，DFIG出力變化參與了系統的振蕩，改變了同步機的阻尼系數，阻尼特性越好，系統抑制振蕩的能力越強。

將式（15）代入到式（2）得到含風機的雙機系統的狀態方程矩陣形式，即

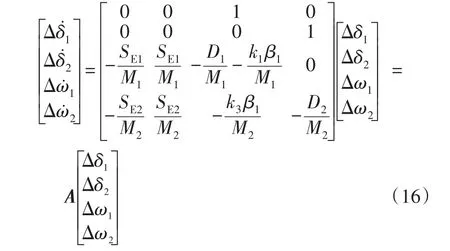
式中：D1、D2分別為同步機1、2的阻尼力矩系數；M1、M2分別為同步機1、2的轉子慣性時間常數；A為狀態方程的系數矩陣。

根據李雅普諾夫第一定律，非線性系統的小干擾穩定性是由矩陣A的特征值所確定的。根據矩陣對角元素之和為該矩陣特征值之和，矩陣A對角線元素之和為系統阻尼之和。可以看出，DFIG接入后系統總阻尼改變量為-k1β1/M1，當k1β1為正值時，DFIG為系統提供正阻尼，有利于系統小干擾穩定；反之，DFIG為系統提供負阻尼，不利于系統小干擾穩定。另外，同步轉矩系數改變也會使各振蕩模式的阻尼分配發生變化。

下面針對DFIG接入改變系統初始平衡點及電氣距離方面，分析DFIG接入對反映系統小干擾穩定性的振蕩模式的影響關系。令 β1=0，根據|λE-A|=0，通過矩陣變換可得

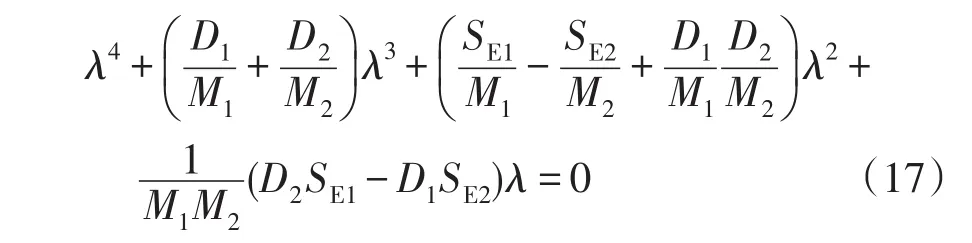
式中，λ為特征值。

假設同步機符合均勻阻尼的條件[12]，即D1/M1=D2/M2=γ，則式（17）簡化為

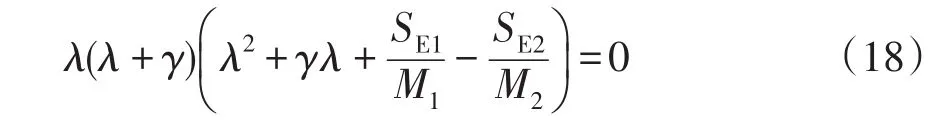
進而求得系統特征方程的根為

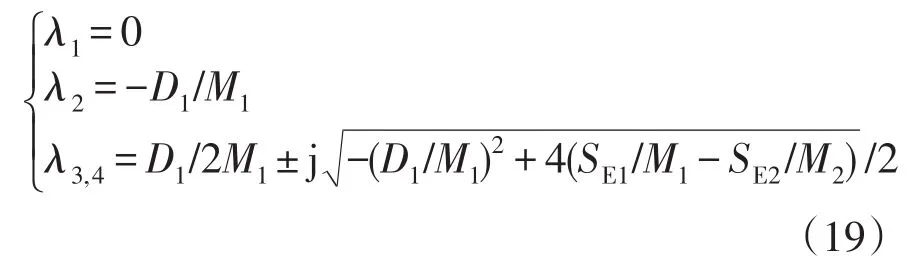
可以看出，零根λ1不反映系統的穩定性特征[13]。當系統正常運行時阻尼D為正值，故λ2為負實數，因此系統的穩定性主要決定于λ3,4。DFIG接入影響了SE1和SE2，定義K=SE1/M1-SE2/M2，K中包含了DFIG的輸出特性及系統初始平衡點等信息。由式（17）可知，系統穩定的判定條件是K>0。當0<4K<(D1M1)2時，λ3,4為兩個負實根；當4K>(D1M1)2時，λ3,4為一對實部為負的共軛復根，K越大，系統振蕩頻率越大，振蕩阻尼比越小。通過以上推導將DFIG接入對系統小干擾穩定性的影響量化到對系統原有振蕩模式的改變。

5 算例分析

5.1 兩機系統仿真

為驗證含有DFIG的電力系統小干擾穩定性分析方法的正確性，在Matlab/Simulink平臺中搭建了如圖1所示的含有雙饋風電場的兩機系統仿真模型。其中，負荷采用恒阻抗模型，同步發電機SG1和SG2的額定功率分別為100 MW和200 MW，單臺DFIG額定功率為1.5 MW，風電場中DFIG臺數根據風電接入容量而變化。分析大型風電場對電網動態穩定影響主要采用的等值動態模型分為單機等值法和多機等值法[14]。本文選用了最常用的單機等值法，將風電場所有的DFIG等值為1臺。另外，風電場出力百分比是在總負荷不變的情況下，風電場替代SG1出力的比例。

5.1.1 理論分析

在本算例中，DFIG正常運行時采用恒功率因數控制，與電網不存在無功功率交換。表1展示了風電場不同出力時等效導納數值及相對功角初始值 δ120。

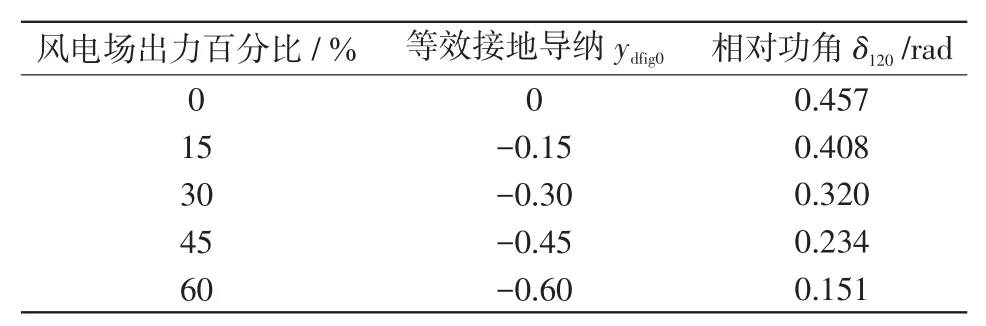
表1 風電場不同出力情況下系統初值Tab.1 Initial value of system under different wind farm output

將算例參數代入節點電壓方程，然后收縮至發電機內電勢節點，進一步根據式（16）計算出風電不同出力情況下系統的機電振蕩模式如表2所示。

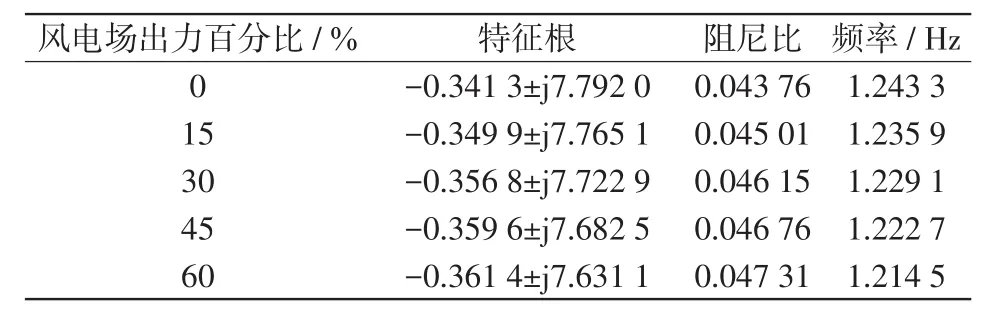
表2 兩機系統機電振蕩模式Tab.2 Electromechanical oscillation mode of two-machine system

由表2可知，所有特征值實部為負數，該系統穩定，進一步發現隨風電接入比例的增加，振蕩頻率呈減小趨勢，阻尼比呈增大趨勢，系統小干擾穩定性增強。這種現象出現的原因主要包括以下兩方面。

（1）風電場出力不同影響了系統總阻尼增量。隨著風電輸出功率增加，風電有功變化量dfig增大，因而 β1增大，同時同步機1、2間的相對功角δ120減小，且改變了同步機的自導納和互導納。由式（14）可知，k1是非線性變化的。本算例的總阻尼增量(-k1β1)為負值，系統阻尼增加，有利于系統小干擾穩定。

（2）根據同步機功角特性曲線，對于穩定運行區域，DFIG接入后同步機有功出力減少，同時由式（10）計算得出的電磁功率增大，靜態穩定儲備系數增加，增強了系統的小干擾穩定性。

5.1.2 仿真驗證

本文仿真分析了DFIG接入前后對系統動態響應的影響。假設當t=0.1 s時節點4處發生三相短路故障，t=0.2 s時切除。在風電場不同出力百分比下SG1和SG2相對功角及SG1有功功率曲線如圖3所示。從相對功角曲線可以看出，風電場接入系統后，同步機組的相對功角的初始值降低，振蕩幅度減小，恢復穩定的時間減小，系統的阻尼特性變好。同樣，SG1有功功率曲線和δ12變化規律基本一致，系統穩定性增強，仿真結果與理論分析結果一致。

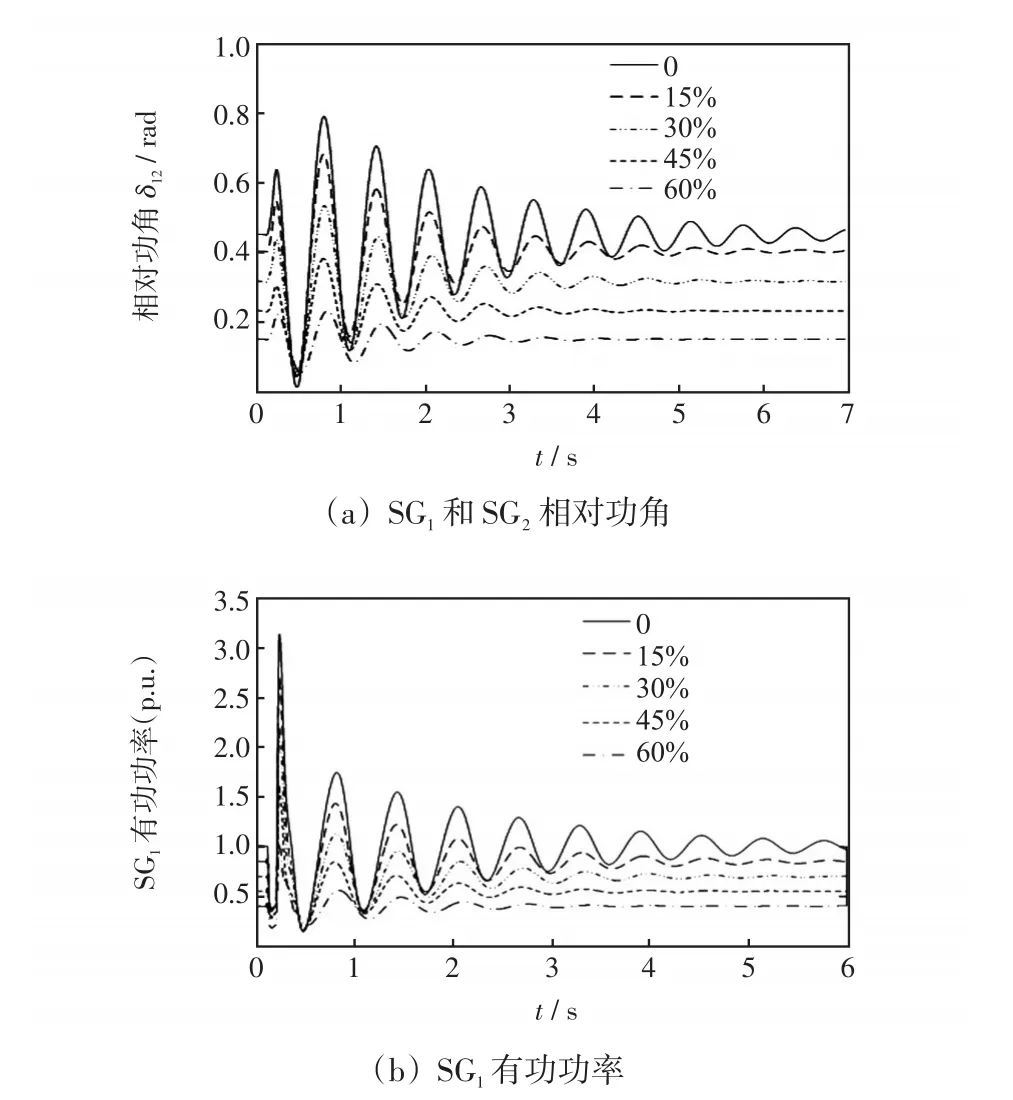
圖3 兩機系統動態響應曲線Fig.3 Dynamic response curves of two-machine system

5.2 多機系統仿真

5.2.1 理論分析

為進一步驗證本文所提方法在多機系統中的適用性，對圖4所示的含有DFIG的三機九節點系統進行仿真分析。SG1、SG2和SG3的額定容量分別為248 MW、192 MW和128 MW。風電場接入節點5，當風電場出力增加時，減少SG2的出力以維持功率平衡。

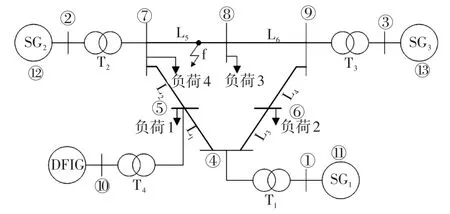
圖4 含DFIG的三機九節點系統結構Fig.4 Structure of three-machine nine-node system with DFIG

在不同出力情況下三機系統的機電振蕩模式如表3所示，圖5為兩個振蕩模式的變化過程。可以看出，系統中包括兩個機電振蕩模式：振蕩模式1隨著風電出力的增加，其阻尼比呈現先增加后減小的趨勢，但總體變化程度不是很大；振蕩模式2隨風電出力增加阻尼比單調增大。

表3 三機系統機電振蕩模式Tab.3 Electromechanical oscillation mode of three-machine system

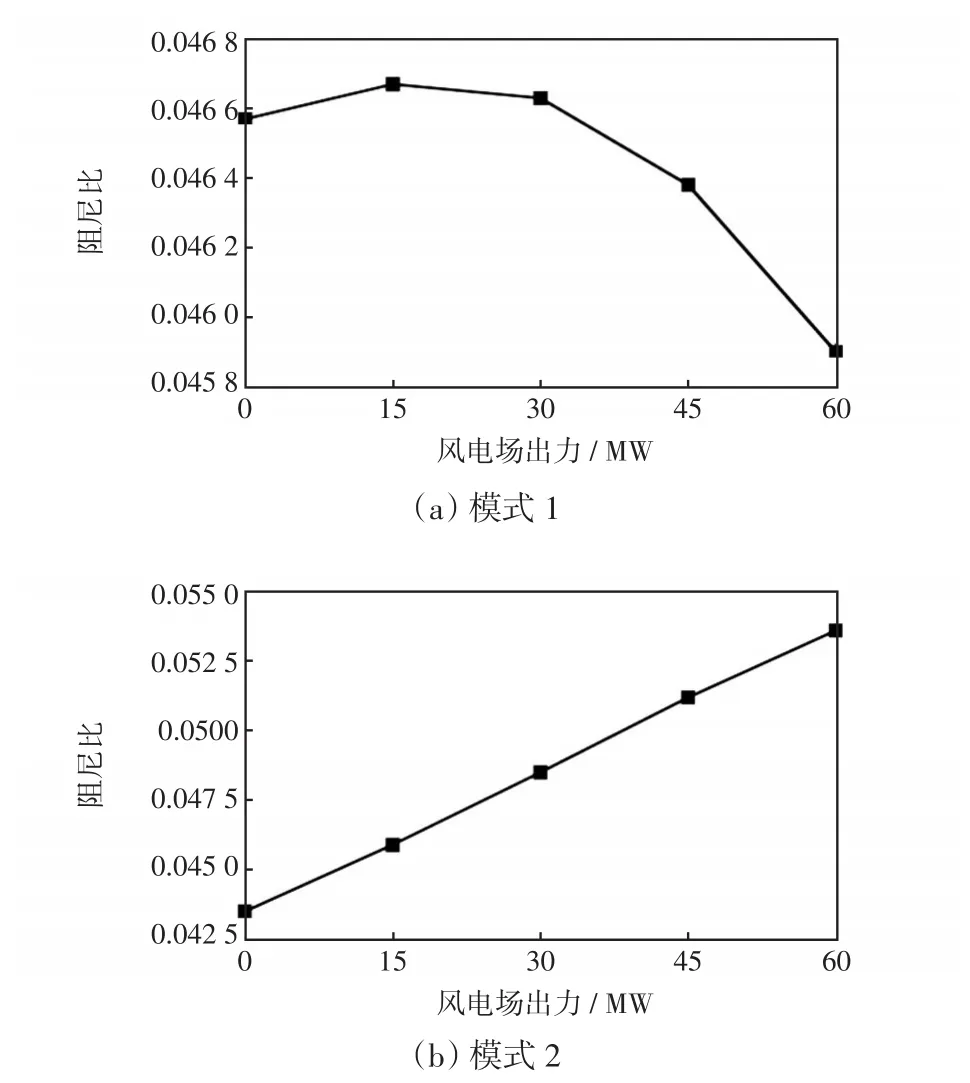
圖5 模式1和模式2的阻尼比變化Fig.5 Changes in damping ratio in modes 1 and 2

影響上述振蕩模式變化的因素主要包括3個方面：①風電出力增加時，對系統平衡點、同步機之間電氣距離以及風電與系統的動態交互作用影響不同，系統阻尼增量呈非線性變化；②SG2出力減少，功角減小，靜態穩定儲備系數增大，同步運行能力增強，有利于系統穩定；③在SG2和SG3之間聯絡線具有相同交換功率的前提下，風電占比增加，系統的阻尼比增強[15]。對于每種振蕩模式來說，上述因素影響程度不同，造成每個振蕩模式的變化趨勢不同。

5.2.2 仿真驗證

假設在t=0.1 s節點8處發生三相短路故障，t=0.3 s時切除，不同風電出力時系統的動態響應如圖6所示，其中不同線型表示0～60 MW風電出力。圖6（a）中SG2和SG1的相對功角δ21曲線顯示隨著風電場出力的增加，δ21首擺幅值越來越小，恢復到穩定狀態的時間越來越短，但當出力達到45 MW和60 MW時，兩條曲線相差不大。圖6（b）中SG2的有功輸出與δ21趨勢基本一致。對于圖6（c）中SG3的有功輸出，當風電接入達到60 MW時，振蕩幅度和恢復穩定的時間都略高于風電接入45 MW時的情況，說明阻尼有所降低，所以需要合理配置風電接入比例，避免系統阻尼特性降低過多而影響系統安全運行。仿真結果與理論計算結果較為吻合。

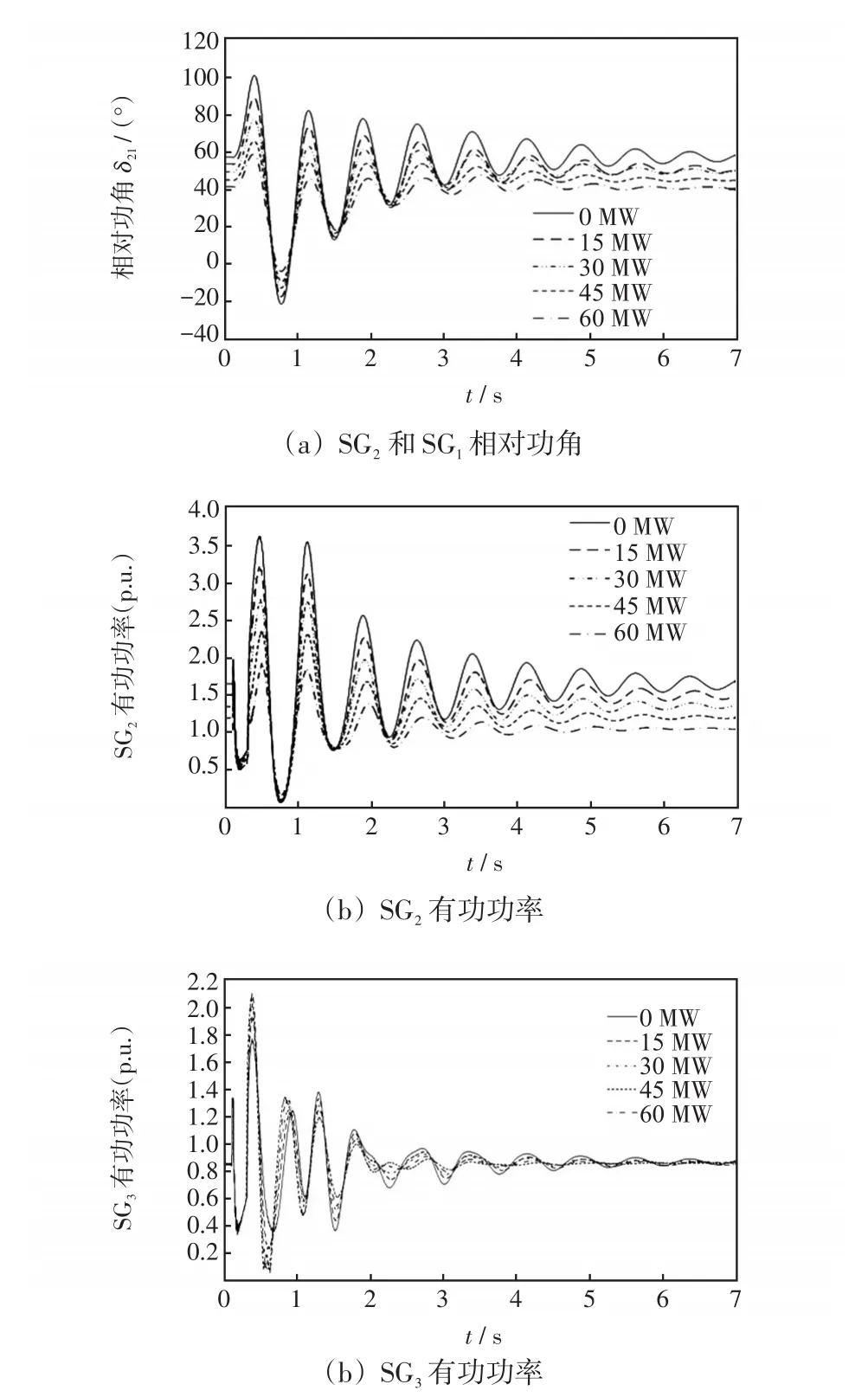
圖6 三機系統動態響應曲線Fig.6 Dynamic response curves of three-machine system

6 結論

本文提出一種含DFIG的電力系統小干擾穩定性分析方法，通過理論與仿真分析得出如下結論。

（1）DFIG具有獨特的運行特性，通過輸出功率實現與電網的交互，其會影響同步機的互同步性，從而影響系統小干擾穩定性。

（2）通過將DFIG輸出特性等效為接地導納和對節點導納矩陣的收縮處理，可將風電場接入信息和輸出特性轉化為對同步機電磁功率和系統原有振蕩模式的影響，從而實現風電場接入對系統小干擾穩定性影響的量化分析。

（3）DFIG的接入改變了系統原有振蕩模式的振蕩特性，并且風電接入比例在一定范圍內增加可改善系統小干擾穩定，這可為含風電場系統的設計規劃提供參考。