極限狀態(tài)下的加筋土擋土墻設(shè)計研究

吳 炫

華設(shè)設(shè)計集團(tuán)股份有限公司，江蘇 南京 210014

極限狀態(tài)設(shè)計方法是基于可靠度理論發(fā)展起來的，1980年我國頒布了相關(guān)技術(shù)標(biāo)準(zhǔn)，使該理論在路基、橋梁、隧道等工程中廣泛應(yīng)用，為極限狀態(tài)設(shè)計方法的發(fā)展起到了促進(jìn)的作用。我國對于極限狀態(tài)理論的研究起步較晚，從理論分析初期至今未形成健全的理論系統(tǒng)。文章基于擋土墻的影響因素的相關(guān)系數(shù)指標(biāo)對擋墻進(jìn)行驗算，推理得到有效的擋墻極限狀態(tài)方程，根據(jù)初步確定的目標(biāo)可靠度可以計算出有關(guān)加筋土擋土墻的表達(dá)式，為我國公路中路基的擋土墻結(jié)設(shè)計構(gòu)提供有效的分析方法和可靠的理論計算依據(jù)。

1 極限狀態(tài)設(shè)計方法

1.1 可靠度理論

可靠性概念定義是路基支擋結(jié)構(gòu)的擋土墻在規(guī)定的使用條件和使用時間內(nèi)，實現(xiàn)結(jié)構(gòu)物自身預(yù)定功能的安全性，對結(jié)構(gòu)物安全性、適用性、耐久性進(jìn)行總體的評價。換言之，結(jié)構(gòu)可靠度的標(biāo)準(zhǔn)是結(jié)構(gòu)物在規(guī)定時間和條件下的安全性、耐久性、適用性的性能得到保證。

可靠度表示支擋物或構(gòu)造物在規(guī)定的條件下和時間內(nèi)，實現(xiàn)結(jié)構(gòu)自身預(yù)定功能的能力，通過字母Ps來表示。可靠概率是對可靠度進(jìn)行定量的描述，通過該指標(biāo)可對可靠度進(jìn)行評價。相反，失效概率是指支擋物或構(gòu)造物在規(guī)定的條件、時間內(nèi)不能完成預(yù)定功能的概率，通過字母Pf來表示。支擋物的失效概率與可靠概率二者相互獨立、互不相容，通過以下公式表達(dá)：

支擋結(jié)構(gòu)應(yīng)保證在設(shè)計使用年限內(nèi)以較為合適的可靠度來滿足規(guī)定的要求，支擋結(jié)構(gòu)要滿足可靠度的要求應(yīng)滿足以下功能：第一，正常施工、正常使用條件下，支擋物或結(jié)構(gòu)物能承受自身重量和外界荷載等作用；第二，結(jié)構(gòu)物受到偶然荷載的作用，結(jié)構(gòu)仍能夠保持整體穩(wěn)定性；第三，正常使用條件下的結(jié)構(gòu)物能夠保持很好的工作性能；第四，結(jié)構(gòu)具有足夠的耐久性。以上條件中，第一條和第二條是承載能力要求，屬于結(jié)構(gòu)的安全性范疇；第三條表達(dá)的是結(jié)構(gòu)的適用性；第四條表達(dá)的是結(jié)構(gòu)的耐久性。以上條件均是正常使用的要求。

1.2 極限狀態(tài)設(shè)計表達(dá)式

擋墻在極限狀態(tài)下時，設(shè)計表達(dá)式的分項系數(shù)，為擋墻支護(hù)結(jié)構(gòu)提供可靠的儲備，采用極限狀態(tài)研究方法，擋墻各參數(shù)的性能計算表達(dá)式如下。

抗傾覆檢算的極限狀態(tài)設(shè)計表達(dá)式：

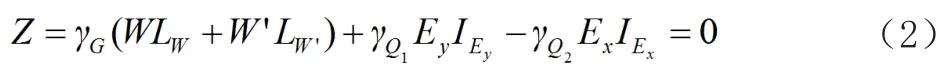
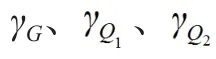
抗滑動檢算的極限狀態(tài)設(shè)計表達(dá)式：

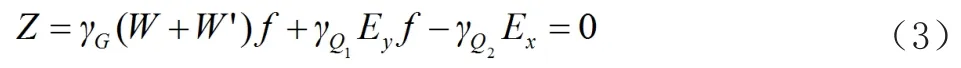
式中：f為摩擦系數(shù)。

抗拉檢算的極限狀態(tài)設(shè)計表達(dá)式：

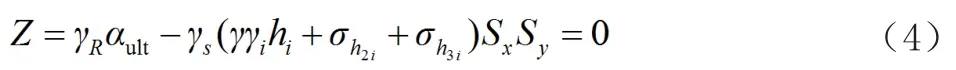
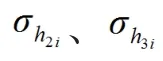
抗拔檢算的極限狀態(tài)設(shè)計表達(dá)式：

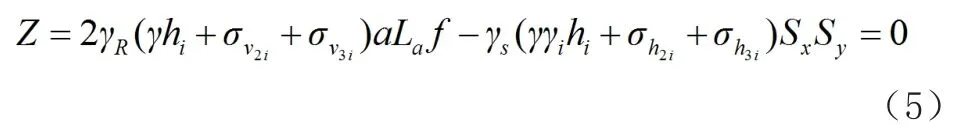
2 極限狀態(tài)方程

2.1 路肩式加筋土擋土墻

（1）抗拔穩(wěn)定性分析。加筋土擋土墻的抗拔穩(wěn)定性采用兩種荷載情況進(jìn)行分析，一種是擋土墻有荷載的情況，另一種是無荷載的情況，還應(yīng)對加筋土擋土墻單根拉筋的抗拔力進(jìn)行計算。加筋土擋土墻受力穩(wěn)定性分析如圖1所示。

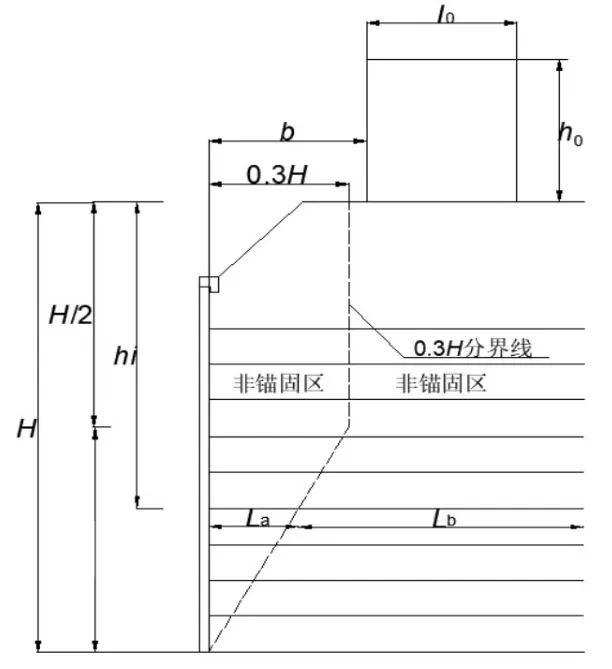
圖1 內(nèi)部穩(wěn)定分析圖（路肩式）

無荷載作用狀態(tài)時，擋墻抗拔性能狀態(tài)表達(dá)式為

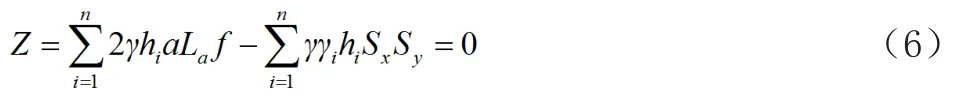
式中：a為筋帶寬度，m；La為筋帶錨固段長度，m；hi為路基頂至第i層填料的距離，m。

極限荷載作用時，擋墻抗拔性能的狀態(tài)表達(dá)式為

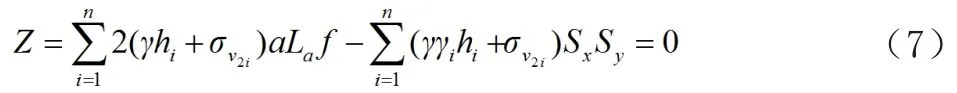
（2）抗拉穩(wěn)定性分析。極限無荷載作用狀態(tài)時，擋墻抗拉性能的狀態(tài)表達(dá)式為

極限荷載作用時，擋墻抗拉性能的狀態(tài)表達(dá)式為

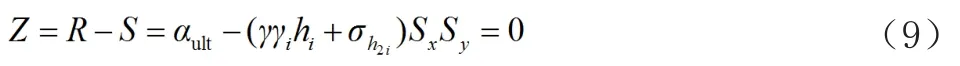
2.2 路堤式加筋土擋土墻

路堤式加筋土擋土墻與路肩式加筋土擋土墻的不同之處在于墻上增加了填土，應(yīng)對其進(jìn)行土柱的換算。其內(nèi)部穩(wěn)定分析圖如圖2所示。

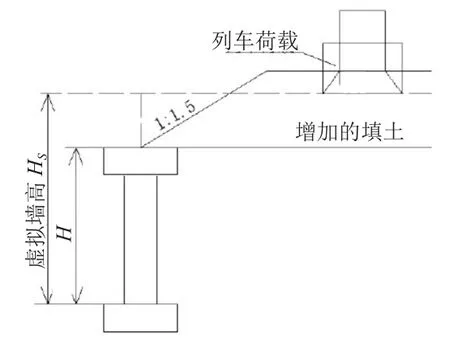
圖2 內(nèi)部穩(wěn)定分析圖（路堤式）

（1）抗拔穩(wěn)定性分析。有荷載作用下，路堤式加筋土擋土墻抗拔穩(wěn)定性的極限狀態(tài)方程同公式（5）。

（2）抗拉穩(wěn)定性分析。有荷載作用下，路堤式加筋土擋土墻抗拉穩(wěn)定性的極限狀態(tài)方程同公式（5）。

3 擋墻分項系數(shù)取值

通過蒙特卡羅法對荷載以及抗力的標(biāo)準(zhǔn)差和變異系數(shù)進(jìn)行相關(guān)統(tǒng)計，最后通過一般分離法對分項系數(shù)進(jìn)行計算。通過分項系數(shù)的計算結(jié)果可知，該系數(shù)的收斂性較好，可以作為分項系數(shù)的建議采取值。對計算結(jié)果以及統(tǒng)計值進(jìn)行分析可以看出，加筋土擋土墻的抗拔分項系數(shù)在不受荷載作用的情況下大于加荷載作用的情況下的分項系數(shù)；加筋土擋土墻的抗拉分項系數(shù)無荷載作用的情況小于有荷載作用的情況。綜合分項系數(shù)如表1所示。

表1 綜合分項系數(shù)

4 極限狀態(tài)設(shè)計表達(dá)式

通過計算結(jié)果可知，擋土墻的分項系數(shù)具有一定的可靠性。將該系數(shù)作為分項系數(shù)的建議值時，其極限狀態(tài)設(shè)計的表達(dá)式如下。

路肩式筋帶抗拔表達(dá)式：

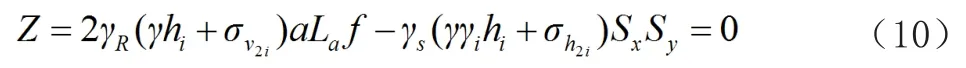
式中，分項系數(shù)γR=0.506，γS=1.16。

路肩式筋帶抗拉表達(dá)式：

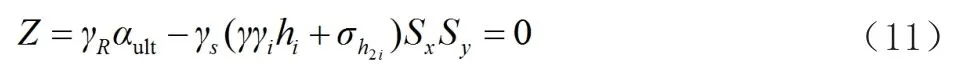
式中，分項系數(shù)γR=0.819，γS=1.235。

路堤式筋帶抗拔表達(dá)式：同公式（5）。

式中，分項系數(shù)γR=0.514，γS=1.166。

路堤式筋帶抗拉表達(dá)式：同公式（4）。

式中，分項系數(shù)γR=0.815，γS=1.269。

5 結(jié)論

文章通過對極限狀態(tài)下的擋墻設(shè)計進(jìn)行分析研究得出以下結(jié)論：（1）擋土墻的可靠度指的是在規(guī)定的條件、時間內(nèi)，實現(xiàn)結(jié)構(gòu)自身預(yù)定功能的能力；（2）文章通過對路堤式加筋土擋土墻和路肩式加筋土擋土墻的抗拉性能和抗拔性能進(jìn)行分析，得到了各自對應(yīng)的極限狀態(tài)方程；（3）分項系數(shù)為結(jié)構(gòu)本身提供了安全儲備，因此文章通過對分項系數(shù)的研究，對分項系數(shù)進(jìn)行了統(tǒng)計分析，得出了綜合分項系數(shù)。對統(tǒng)計值進(jìn)行分析得到結(jié)論：不加外荷載抗拔穩(wěn)定性、極限加載抗拉穩(wěn)定性滿足要求。該結(jié)論與極限狀態(tài)假設(shè)擋墻的受力情況計算結(jié)果相符，表明此研究中的分項系數(shù)取值合理。