基于統計損傷理論的飽和土鄧肯-張修正模型

葉薇，蘆婷婷，江信東，黃安邦

(1.寧波寧大地基處理技術有限公司，浙江 寧波 315211；2.中國建筑西南勘察設計研究院有限公司，四川 成都 610052；3.中國地質調查局 地質災害防治技術中心，四川 成都 611734)

本構模型是土力學中的核心內容，近年來受到學者廣泛關注[1-2]。Krajcinovic等[3]、唐春安[4]和曹文貴等[5]國內外學者將統計學和損傷力學有機結合，提出統計損傷本構模型并應用到巖土體材料本構關系模擬中，取得了良好的成效。飽和土是一種固-液二相體系材料，其內部空隙被水充填，在外界荷載作用下易發生變形破壞，對基礎工程、巖土工程等的安全建設及營運造成威脅。模擬飽和土的本構關系，可為深入認識飽和土工程力學特性提供參考。

目前對飽和土本構關系研究已有較多成果，莫瑞[6]在巖石統計損傷模型的基礎上，引入飽和土有效應力原理，得到飽和土統計損傷本構模型；曹文貴等[7]結合巖石統計損傷模型構建方法，構建在特定圍壓下的飽和土統計損傷本構模型；胡小榮等[8]在三剪統一強度準則的基礎上，結合劍橋模型，得到飽和砂土三剪彈塑性邊界面模型；鄧岳保等[9]基于飽和土熱固結響應，得到新的可反映溫度變化的有效應力原理。

目前已有一些飽和土統計損傷模型相關成果，但多是通過巖石統計損傷模型構建方法，引入有效應力原理而得，其模型內在的性質可能存在與飽和土相悖的地方。鄧肯-張模型是一種基于試驗成果的線性本構模型，在土體本構關系描述中廣泛應用，但鄧肯-張模型由于自身局限性無法反映土體內在性質的變化。鑒于此，本文基于傳統鄧肯-張模型，引入統計損傷理論，建立一種新的飽和土鄧肯-張統計損傷模型。通過鄧肯-張統計損傷模型描述飽和土變形，為飽和土變形破壞過程深層次認識提供參考。

1 常規三軸固結排水試驗

采用CSS-2901TS型土體三軸試驗機開展固結排水常規三軸壓縮試驗，土樣取自某邊坡，該邊坡長期受庫水位影響處于飽和狀態，取樣密封后運回實驗室制作成φ40 mm×80 mm的真空飽水重塑樣。土樣的平均濕密度和干密度分別為2.07 g/cm3和1.58 g/cm3，孔隙比為1.5，壓縮模量為24.157 MPa，黏聚力為0.035 MPa，內摩擦角為20°。根據試樣所處應力環境，取試驗圍壓為100、200、300和400 kPa。三軸固結排水試驗結果如圖1所示。

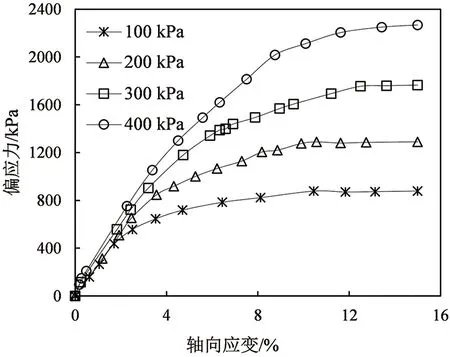
圖1 偏應力-應變曲線Fig.1 Deviatoric stress-strain curve

由圖1可知，偏應力-應變曲線形態近似為雙曲線，當土樣處于低應力狀態時，曲線近線性；處于高應力狀態時，曲線逐漸偏于應變軸，表現出一定非線性特征。鄧肯-張模型是一種基于試驗成果的線性本構模型，從土體內部性質而言，鄧肯-張模型無法體現飽和土體的非線性力學性質，但該模型也存在著參數少、結構形式簡練的優點。故本文選擇鄧肯-張模型為基礎模型，引入統計損傷理論，將線彈性模型改進為反映土體損傷累積連續不可逆的非線性模型，從而得到飽和土修正鄧肯-張模型。

2 基于統計損傷理論的鄧肯-張修正模型

依據Lemaitre[10]等效應變原理，假定宏觀應力σ作用在損傷材料上，其產生的應變ε與有效應力σ′引起無損材料的應變ε′相等，即

ε=ε′。

(1)

土體實際上處于三維應力狀態，于是有

σ′=σ/(1-D)，

(2)

式中，D為損傷變量。

傳統鄧肯-張模型的本構方程為

(3)

式中，a、b為試驗參數。

結合式(2)、(3)可得

(4)

考慮到土體內部微缺陷發展具有隨機分布特性，引入統計損傷理論，假定微元強度F=f(σ′)[11]服從某概率分布P(F)，于是損傷變量D為

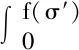
(5)

式中，F為土體微元強度的隨機分布變量，F的概率密度函數為P(F)。

統計損傷理論中，應用較多的概率分布主要有Weibull分布、冪函數分布、正態分布等，唐春安[4]發現Weibull概率密度分布可能存在尺寸效應不適用的情況，陳立宏等[12]認為正態分布可能使強度為負，而冪函數分布結構簡單，且參數少，形式簡單，故本文采用冪函數概率密度分布

(6)

將式(6)代入式(5)得

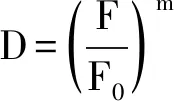
(7)

假定微元強度F遵守Mohr-Coulomb強度準則

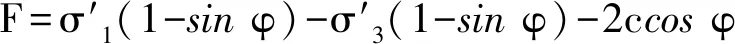
(8)

式中，c為黏聚力，φ為內摩擦角，第1節中已給出。

聯立式(4)、(7)可得

(9)

式(9)即為本文基于統計損傷理論的鄧肯-張修正模型。

3 模型參數確定方法

修正模型包含a、b、m和F0共4個參數，其中a、b為鄧肯-張模型中的試驗參數，m、F0為統計分布參數。

3.1 參數a、b求解

根據鄧肯-張模型參數確定方法，a為初始切線模量Eu的倒數

(10)

參數b為極限偏差應力(σ1-σ3)ult的倒數

(11)

偏應力-應變曲線中的漸近線所對應的縱軸值即為極限偏差應力(σ1-σ3)ult。參數a、b的確定方法如圖2所示(以圍壓400 kPa偏應力-應變數據為例)，試驗參數a和b值如表1所列。

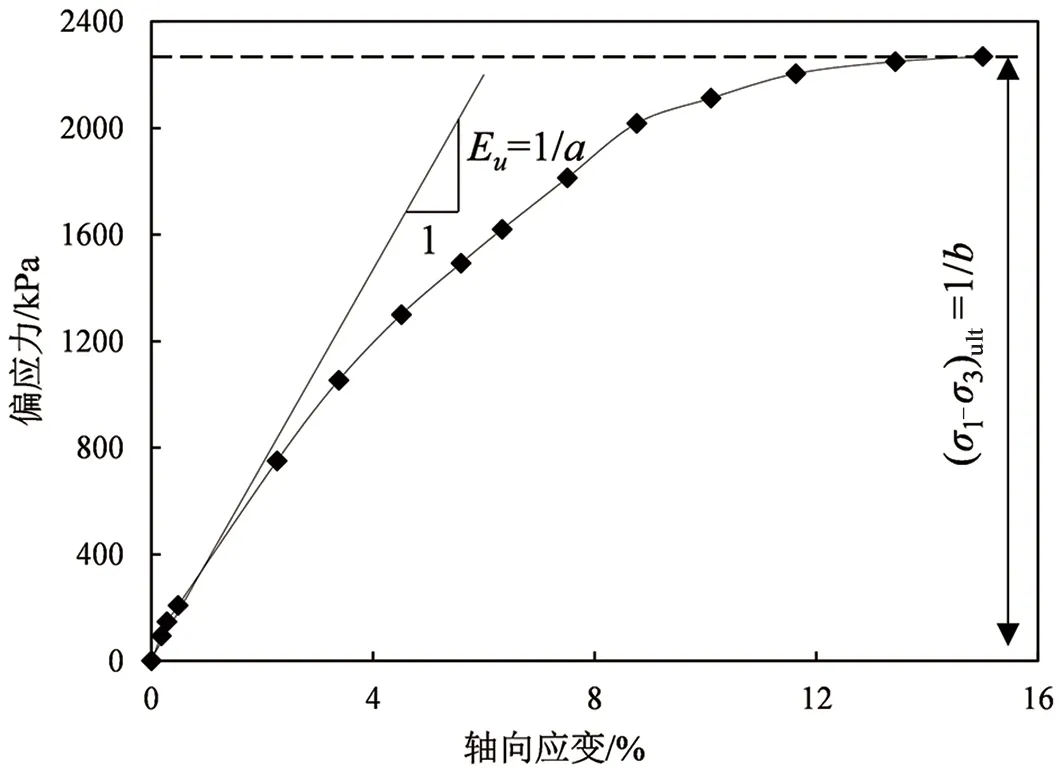
圖2 參數a和b求解示意圖Fig.2 Schematic of solution for parameters a and b solution

表1 參數a和b值Table 1 Values of parameters a and b

3.2 參數m、F0求解

式(9)可變形為

(12)

在式(12)等號兩側同時取對數得

(13)

式(13)可變形為如下線性方程形式

Y=mX+P，

(14)

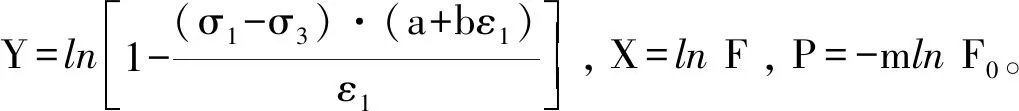
通過上述線性擬合方法，得到擬合結果如表2所列。

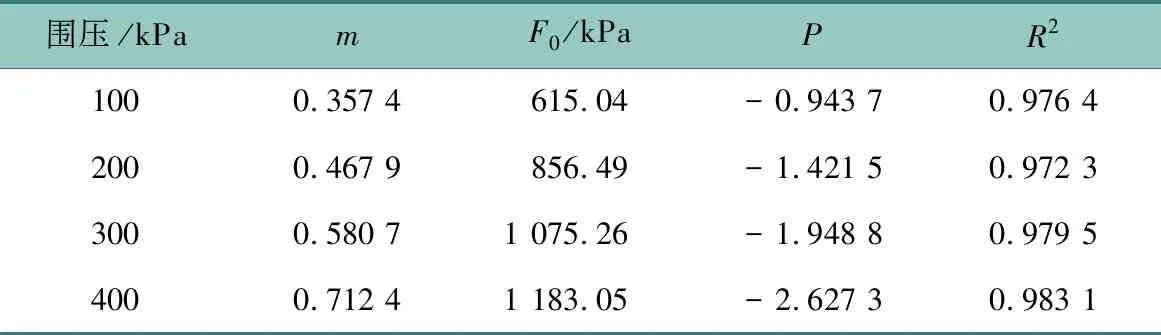
表2 參數m和F0值Table 2 Values of parameter m and F0

4 模型驗證

為驗證本文基于統計損傷理論的鄧肯-張修正模型的可行性，將修正模型與傳統鄧肯-張模型同時對本文飽和土偏應力-應變曲線進行辨識驗證，辨識結果如圖3所示。

從圖3中分析可得，本文基于統計損傷理論的鄧肯-張修正模型的辨識能力較好，擬合精度較高，平均R2達到0.987 4，傳統鄧肯-張模型擬合效果次之，R2僅有0.925 3，且對偏應力-應變曲線中應變4%～12%段的曲線擬合偏差較大。為了驗證本文所建模型對不同飽和土的適用性，引用文獻[6]中飽和土相關試驗數據，通過本文所建模型進行辨識，得到試驗值和理論值對比曲線，如圖4所示。

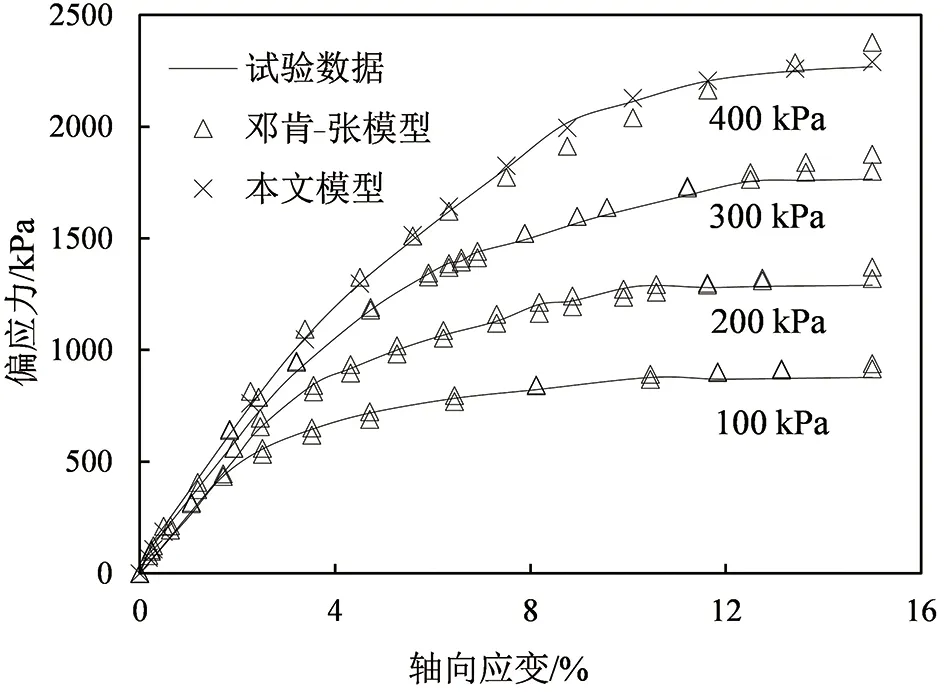
圖3 模型辨識結果對比Fig.3 Comparison of model identification results

由圖4可看出，傳統鄧肯-張模型的R2為0.903 5，在軸向應變0～13%之間，理論值明顯低于試驗曲線，在軸向應變13%～18%之間，理論值明顯高于試驗曲線，存在較大偏差。而本文所建模型的R2為0.981 3，相比傳統模型，擬合精度更高，能較好地描述飽和土變形全過程。

傳統鄧肯-張模型為線性模型，不具備反映飽和土內在性質變化的特點。本文在傳統鄧肯-張模型的基礎上引入了統計損傷理論，得到基于統計損傷理論的鄧肯-張修正模型，該模型具有良好的曲線辨識能力，能較為準確地描述飽和土的變形全過程，使模型內涵更為豐富。

5 結論

通過研究得出以下結論：

(1)開展了飽和土常規三軸固結排水試驗，其偏應力-應變曲線形態近似為雙曲線，當土樣處于低應力狀態時，曲線近線性，處于高應力狀態時，曲線逐漸偏于應變軸，表現出一定非線性特征。

(2)根據飽和土非線性特性，選擇鄧肯-張模型為基礎模型，引入統計損傷理論，得到改進后的修正模型。依據鄧肯-張模型自身特性和參數線性擬合的方法，確定模型參數。

(3)本文的修正模型沿用了傳統鄧肯-張模型的模型框架，具有結構簡單、參數較少的特點，便于應用。采用修正模型和傳統模型對飽和土試驗數據進行辨識驗證，對比辨識效果，證明了修正模型的可行性和合理性。