快速傅里葉變換在信號處理中的應(yīng)用

於 璽

（同濟(jì)大學(xué)浙江學(xué)院 浙江 嘉興 314000）

1 引言

傅里葉變換在信息學(xué)科擁有很高地位。但計(jì)算機(jī)只能處理離散且有限長序列，因此它在離散域中的表達(dá)形式—離散傅里葉變換（discrete fourier transform，DFT）產(chǎn)生了。離散傅里葉變換可以直接用來進(jìn)行計(jì)算分析工作，因此在數(shù)字信號處理中，常常會(huì)用到此方法來分析信號頻譜、計(jì)算頻率響應(yīng)等。1965年，快速傅里葉變換算法（fast fourier transform，F(xiàn)FT）首次被提出。在對速度要求沒有非常高的情形下，F(xiàn)FT基本上可以滿足工業(yè)應(yīng)用的要求。在處理數(shù)字信號時(shí)，常常可以用離散傅里葉變換來實(shí)現(xiàn)它的運(yùn)算，所以快速傅里葉變換算法之于數(shù)字信號處理具有不可替代的作用。因此，在快速傅里葉變換誕生之后，數(shù)字信號處理技術(shù)的發(fā)展越加迅速、應(yīng)用范圍也越加廣泛，幾乎滲透進(jìn)了社會(huì)生產(chǎn)和生活的方方面面。

2 國內(nèi)研究現(xiàn)狀

張玲佳[1]在對FFT算法的原理及FFT硬件加速器的影響因素進(jìn)行研究之后，對高維度FFT加速器進(jìn)行了設(shè)計(jì)及硬件實(shí)現(xiàn)。在雷達(dá)信號處理領(lǐng)域，為實(shí)現(xiàn)動(dòng)目標(biāo)檢測技術(shù)，謝輝輝[2]設(shè)計(jì)了一種可變點(diǎn)和一種定點(diǎn)FFT處理器。在圖像融合領(lǐng)域，曹端良[3]提出一種改進(jìn)的HIS+SWT算法，此外，還提出一種改進(jìn)的快速傅里葉變換的泊松圖像融合算法。在頻譜分析方面，邢鑫[4]對基于FFT的頻譜細(xì)化算法進(jìn)行了深入研究。在電力系統(tǒng)下，為減少諧波污染問題，張旭東[5]基于FFT的諧波檢測算法提出加6項(xiàng)組合余弦窗雙譜線插值修正諧波檢測算法。黃純等[6]提出分通道分時(shí)段壓縮方案，以減少電力系統(tǒng)中大量故障數(shù)據(jù)的傳輸問題。在對色譜噪聲進(jìn)行平滑方面，楊黎等[7]將FFT法與其他數(shù)字濾波法進(jìn)行比較后發(fā)現(xiàn)，F(xiàn)FT法能更好進(jìn)行噪聲平滑處理，并使信噪比提高18倍。在對圖像中的噪聲進(jìn)行平滑方面，林志斌等[8]提出一種新的基于OGSTV的圖像去噪方法，該法加入了FFT理論后，大大縮短了去噪時(shí)間。此外，陸文祺[9]深入研究了基于高階模型的圖像去噪，此外對其快速算法進(jìn)行了分析。在軌道電路移頻信號檢測上，安義巖[10]提出基于帶通采樣的FFT軌道移頻信號調(diào)解算法以提高解調(diào)精確度。

3 快速傅里葉變換FFT原理及其優(yōu)越性

3.1 快速傅里葉變換FFT原理

模擬信號x（t）連續(xù)傅里葉變換：

x（t）T個(gè)抽樣周期后變?yōu)閤（nT）。設(shè)x（n）為N點(diǎn)有限長序列。

其DFT為：

由上式可見，接下來運(yùn)算十分復(fù)雜。

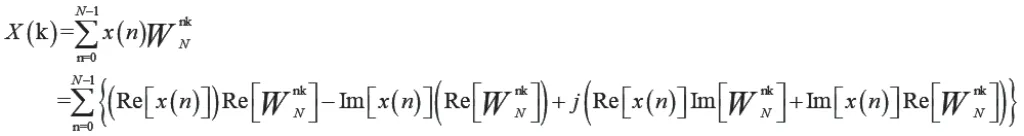
3.2 快速傅里葉變換的優(yōu)越性

計(jì)算的工作常常通過計(jì)算機(jī)來進(jìn)行。在使用傅里葉變換進(jìn)行復(fù)雜運(yùn)算時(shí)，計(jì)算機(jī)往往會(huì)因?yàn)檫\(yùn)算負(fù)擔(dān)過大而導(dǎo)致高耗電量。因此，運(yùn)算速度相對較慢的計(jì)算機(jī)系統(tǒng)常常對此敬而遠(yuǎn)之。而由于快速傅里葉變換對運(yùn)算的低要求及其運(yùn)算快的優(yōu)點(diǎn)，使得FFT在生產(chǎn)和生活中作用都極其巨大。

4 快速傅里葉變換在信號處理中的應(yīng)用

信號處理，簡言之，就是人們?yōu)榱说玫接杏眯畔ⅲ鴮υ盘栠M(jìn)行一系列處理的方式。以下是對FFT在信號處理中的應(yīng)用進(jìn)行的分析與總結(jié)。

4.1 用FFT進(jìn)行離散信號壓縮

FFT算法壓縮比高，因而可以用其進(jìn)行信號壓縮。快速傅里葉變換可以在某個(gè)給定的錯(cuò)誤容限下，把小于相應(yīng)閾值的快速傅里葉變換系數(shù)置零，從而減少需要傳輸?shù)南禂?shù)，最后實(shí)現(xiàn)壓縮。例如，大量故障錄波數(shù)據(jù)常會(huì)出現(xiàn)在電力系統(tǒng)中。龐大數(shù)量的故障錄波數(shù)據(jù)會(huì)使得之后存儲(chǔ)和實(shí)時(shí)傳輸故障信號會(huì)變得十分困難，而壓縮錄波數(shù)據(jù)的方法可以大大改善這一問題。

4.2 用FFT實(shí)現(xiàn)快速卷積

卷積在分析數(shù)學(xué)中有重要作用，常被用來進(jìn)行信號分析。如果f（x）、g（x）為 (實(shí)數(shù)集)上兩個(gè)可積函數(shù)，對其作積分：

則稱F(x)為函數(shù)f（x）、g（x）的卷積。常表示為F（x）=f（x）*g（x）。

對于定義在 Z（整數(shù)集）上的函數(shù)f 、g，卷積定義為：

卷積定理：如果兩個(gè)時(shí)間序列h（k）和x（k）分別為 H（m）和X（m），那么h（k）*x（k）的DFT為H（m）點(diǎn)乘X（m），H（m）點(diǎn)乘X（m）的IDFT為h（k）*x（k）。應(yīng)用快速傅里葉變換實(shí)現(xiàn)快速卷積，簡言之，是將N點(diǎn)的DFT不斷等分到很小，計(jì)算2點(diǎn)、4點(diǎn)或混合基的DFT，此法能使DFT的計(jì)算難度降低。

4.3 用FFT進(jìn)行諧波檢測

隨著經(jīng)濟(jì)的迅猛發(fā)展、各類電力電子設(shè)備的廣泛使用，電力系統(tǒng)的污染比如諧波問題也日漸嚴(yán)重。快速傅里葉變換常常被用來檢測基波和整數(shù)次諧波，從而進(jìn)行諧波檢測。

盡管基于FFT的諧波檢測算法應(yīng)用范圍廣，但其也存在局限，比如FFT法存在較大誤差。此外，F(xiàn)FT法還需一定時(shí)間進(jìn)行采樣。為了使FFT法的計(jì)算準(zhǔn)確率和計(jì)算速度有所提升，目前，改進(jìn)方法有加窗插值算法、雙峰譜線修正算法和組合方法。此外，針對此法的局限性，許多學(xué)者提出了許多能夠起到明顯效果的小策略，如張旭東[5]提出的優(yōu)化算法。

4.4 用FFT進(jìn)行去噪

在各領(lǐng)域進(jìn)行信號檢測，都會(huì)產(chǎn)生一定噪聲信號，以下以色譜、圖像兩方面的信號去噪為例。

色譜數(shù)字信號除了包含檢測器對所分析的樣品產(chǎn)生的響應(yīng)信號，還包含整個(gè)系統(tǒng)帶來的噪聲信號，這使得色譜峰的檢測、判別與數(shù)據(jù)處理變得困難。在對色譜信號進(jìn)行去噪方面，使用快速傅里葉變換能大大縮短檢測時(shí)間、提高檢測靈敏度。

在圖像去噪方面，由于圖像常會(huì)產(chǎn)生不同的噪聲，為了得到清晰優(yōu)質(zhì)的圖像，我們需要在圖像處理之前對其進(jìn)行去噪處理，使用FFT對其在頻域進(jìn)行操作是一種有效的方式。將圖像進(jìn)行傅里葉變換使其轉(zhuǎn)化到頻域，我們可以將得到的圖像像素中高頻部分的幅值置為0，同時(shí)只保留低頻部分幅值，圖像噪聲從而得以簡單去除，使得圖像得到一定平滑，但此法未能精確去除噪聲。因此，也產(chǎn)生了許多基于FFT的新算法，如林志斌[8]在傳統(tǒng)OGSTV的圖像去噪方法中引入了FFT，使得圖像去噪時(shí)間大大縮減。

4.5 關(guān)于FFT的硬件實(shí)現(xiàn)

在合理利用硬件特性的基礎(chǔ)上，硬件加速器能夠使計(jì)算更為快速。而硬件本身存在一定的局限性，如內(nèi)存、成本等方面。因此許多學(xué)者針對這一局限，提出了自己的想法，如張玲佳[1]在文獻(xiàn)中提出了一種高速、低資源消耗的變維度FFT硬件加速器。這種硬件加速器可以很好地適應(yīng)復(fù)雜數(shù)字信號處理對不同維度、不同點(diǎn)數(shù)的快速傅里葉變換計(jì)算任務(wù)。

4.6 用FFT進(jìn)行信號檢測

雷達(dá)探測的環(huán)境中通常都充斥著各種雜波，進(jìn)而干擾雷達(dá)探測到的結(jié)果。因此我們需要通過動(dòng)目標(biāo)檢測以濾除干擾項(xiàng)、保留運(yùn)動(dòng)目標(biāo)的回波。在雷達(dá)信號領(lǐng)域，F(xiàn)FT常用于濾波。由文獻(xiàn)[2]動(dòng)目標(biāo)檢測常使用多普勒濾波器組FIR橫向數(shù)字濾波器進(jìn)行濾波。為了提高運(yùn)算效率、簡化實(shí)現(xiàn)過程，快速傅里葉變換算法大大降低運(yùn)算要求，同時(shí)大大縮小了所需硬件面積。而此法在檢測性能上有局限性，因此常常將其與MTI配合使用。此外，F(xiàn)FT濾波器組在靈活性、抑制雜波能力等方面也有一定局限，在這些方面仍需深入研究。

在軌道交通領(lǐng)域，常需要檢測列控系統(tǒng)中的移頻信號，以判斷軌道區(qū)段是否占用，從而防止錯(cuò)誤辦理。然而，軌道電路中的信號檢測常受到牽引電流和相鄰軌道區(qū)段的移頻信號的影響。因此，想對其進(jìn)行信號檢測，首先需要進(jìn)行信號解調(diào)，使用FFT算法的頻域檢測法目前常用于信號解調(diào)。目前，許多學(xué)者在此基礎(chǔ)上對移頻信號檢測技術(shù)進(jìn)行了優(yōu)化，如安義巖[10]提出基于帶通采樣的FFT軌道移頻信號調(diào)解算法，使解調(diào)精確度進(jìn)一步提高。

5 結(jié)語

本文對快速傅里葉變換算法進(jìn)行了分析，并詳述了FFT在信號處理中的應(yīng)用。快速傅里葉變換運(yùn)算高效便捷，為信號處理提供了良好的條件。