基于MATLAB的系統穩定性分析的演示程序設計

燕麗鴿，孫園志，王志鵬（通訊作者）

（南陽師范學院物理與電子工程學院 河南 南陽 473061）

1 引言

系統若要實現其自身的功能，必須具有穩定系統。若一個系統的輸入是有界的且輸出也是有界的則該系統為穩定系統。若系統不是穩定系統，其輸出無界，此時系統為非線性系統；設備無法承受極大的輸出，進而系統不僅不能處于我們所需的工作狀態，也可能會損毀設備[1]。因而，事先判斷系統是否穩定就格外重要。判斷系統是否穩定的方法有很多，在控制理論中，判斷系統是否為穩定系統的判據為傳遞函數的極點在復平面左邊。

利用經典傳統方法判斷一個系統的穩定性，是復雜且繁瑣的，且難以達到證明目的。其一是因為計算量太大，難以高效進行；其二是傳統方法無法得到強信服力的圖形來支撐觀點加以論證。若是人工計算，可能只是判斷是否穩定，而不能準確地畫出直觀的圖形以及得到一些準確的數據。所以，人們提出很多輔助方法來幫助判斷系統穩定性，例如勞斯判據、繪制根軌跡、波特圖等[2]。在控制系統穩定性時，由于精準數值的要求使解得該系統的階躍響應是困難的，且難以描繪精確直觀的頻率響應曲線，所以便可借助電腦軟件MATLAB進行計算以及描繪曲線，同時也可以對系統性能有某些影響的參數進行研究[3]。

此外，MATLAB該軟件實驗界面友好，操作很簡單，圖形界面設計一目了然，所占內存小，容易上手使用，還可用于系統分析和系統設計的教學實驗。在MATLAB的GUI窗口圖形界面可以自主設計，通過設計界面、調用函數完成演示。通過觀察GUI演示界面可以簡單、快速、直觀、有效地判斷一個系統是否穩定。在MATLAB軟件中，其函數庫提供了大量的數學公式，可省去人工計算，大大減少誤差，并且極大地方便進行各種計算及描繪圖形；庫中還包含有圖形繪制的函數，這樣便得到足以支撐論證且精確的圖形，使得經典控制中判斷系統穩定性變得簡單[4]。

2 演示程序的總體結構

根據《信號與系統》課程的一些知識，若一個連續或離散系統是有界輸入有界輸出，那么該系統是穩定的。在眾多的經典系統中，可以通過多種方法來判斷一個系統是否穩定[1]，在本文中選取了零極點圖[5]、根軌跡法、波特圖[6]這3種方法來進行演示。該演示程序設計的總體結構框圖見圖1，點擊每一個按鈕，都可以分別打開不同的系統穩定性分析子模塊。

圖1 演示程序設計的主頁面圖

3 子模塊介紹

3.1 零極點圖

在一個線性是不變系統中，若系統的傳遞函數H（s），其所求解的所有極點均位于復平面的左半平面內，出現在時域響應e的指數部分，因為傳遞函數極點的實部都小于0，伴隨著時間函數的逐漸變大，其結果會逐漸趨于0，因此該系統是穩定的。對應在時域中，極點的實部小于0，是個振蕩衰減的函數，最后一定會穩定。

在離散系統中，在求解其所對應的系統函數H（z）后，其收斂域包含單位圓，則該系統是穩定系統；若對系統輸入任意有界的序列，系統輸出也是有界的，那么該系統是穩定的。

演示程序設計的零極點圖圖形界面見圖2。

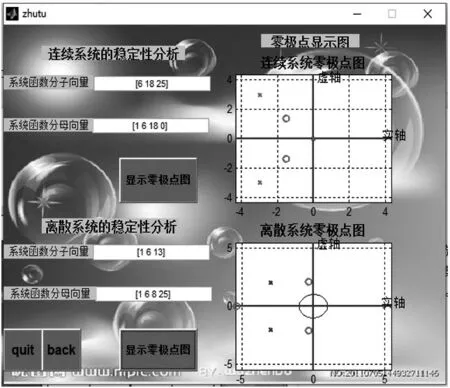
圖2 演示程序設計的零極點圖圖形界面

該GUI程序可以通過在動態文本框里輸入系統函數的分子、分母向量后，點擊對應按鍵，可以分別對應顯示連續、離散系統的零極點圖顯示在坐標軸上，通過點擊back按鍵，可以返回到主界面，若不再進行演示，通過點擊quit按鍵退出GUI程序演示界面。

利用零極點圖判斷連續系統穩定性的回調函數如下：

axes(handles.axes1)；

a1=handles.axes1；

cla(a1)；

plot([-x x]，[0 0]，'b-'，'LineWidth'，2)；

hold on；

plot([0 0]，[-y y]，'b-'，'LineWidth'，2)；

plot(real(p)，imag(p)，'rx'，'LineWidth'，2)；

plot(real(q)，imag(q)，'ro'，'LineWidth'，2)；

利用零極點圖判斷離散系統穩定性的回調函數如下：

axes(handles.axes2)；

a2=handles.axes2；

cla(a2)；

hold on；

w=0:pi/200:2*pi；

b=exp(i*w)；

plot(b)；

plot([-x x]，[0 0]，'LineWidth'，1.5)；

plot([0 0]，[-y y]，'LineWidth'，1.5)；

plot(real(p)，imag(p)，'rx'，'LineWidth'，2)；

plot(real(q)，imag(q)，'ro'，'LineWidth'，2)；

3.2 根軌跡法

繪制根軌跡的主要思路就是根據其特征方程的性質與零極點和參數的關系，總結根軌跡的規律便可畫出根軌跡圖和變化趨勢。繼前言，描制圖形依然可用MATLAB繪出；在其函數庫中，直接提供了求取函數零極點的函數以及繪制根軌跡的函數（rlocus、rlocfind、pzmap等），所以我們可以根據所繪制的零極點圖在平面的分布情況直接判斷該系統是否穩定[2]。

演示程序設計的根軌跡法圖形界面見圖3。

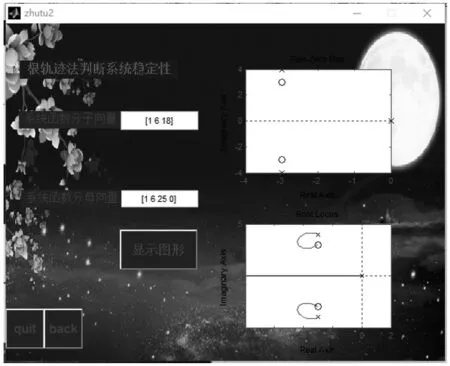
圖3 演示程序設計的零極點圖圖形界面

該GUI程序可以通過在動態文本框里輸入系統函數的分子、分母向量后，點擊顯示圖形按鍵，可以在兩個坐標軸上顯示零極點圖和根軌跡圖，通過點擊back按鍵，可以返回到主界面，若不再進行演示，通過點擊quit按鍵退出GUI程序演示界面。

根軌跡法的回調函數：

g=tf(A，B)；

axes(handles.axes2)；

ax_2=handles.axes2；

cla(ax_2)；

hold on；

rlocus(g)；

axes(handles.axes1)；

ax_1=handles.axes1；

cla(ax_1)；

hold on；

pzmap(g)；

3.3 波特圖

波特圖又稱對數頻率特性曲線，波特圖是線性系統的傳遞函數對頻率的半對數坐標圖。利用波特圖可以觀察系統的頻率響應，包括幅頻響應和相頻響應曲線圖[2]。利用波特圖進行穩定性判定的依據是：幅值裕度GM＞0且相角PM裕度＞0，但是使用該判據進行穩定性判定必須滿足一個前提條件：系統的開環傳遞函數必須為最小相位系統。

演示程序設計的波特圖圖形界面見圖4。

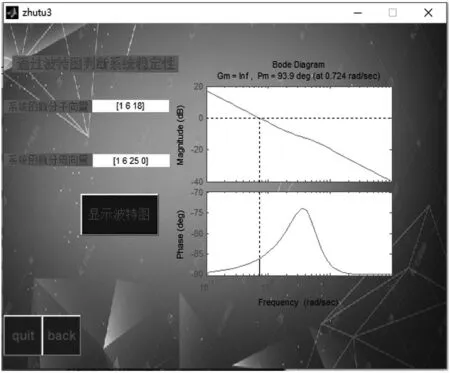
圖4 演示程序設計的零極點圖圖形界面

該GUI程序可以通過在動態文本框里輸入系統函數的分子、分母向量后，點擊顯示波特圖按鍵，可以顯示出該系統的波特圖以及頻率圖，通過點擊back按鍵，可以返回到主界面，若不再進行演示，通過點擊quit按鍵退出GUI程序演示界面。

波特圖的回調函數：

g=tf(A，B)；

axes(handles.axes1)；

ax_1=handles.axes1；

cla(ax_1)；

hold on；

bode(g)；

margin(g)；

4 結語

本文采用了計算機 MATLAB軟件，通過GUI窗口設計，調用函數的方法進行系統穩定性的判斷。采用了系統的開環傳遞函數，求解其函數特征方程的零、極點、閉環特征根，在時域、頻域中繪制圖形，對系統穩定性進行判別研究。設計了零極點、根軌跡、波特圖的GUI界面，可以實現對系統穩定性的判定，具有操作簡單、顯示直觀、易懂、精準的優點，避免了傳統方法的繁瑣、不準確以及一些誤差，更便于使用。在此過程中，既避免了繁瑣的分析計算過程，極大地提高了可信度，又可通過計算機繪制圖形，得到有信服力的圖形來支持論證，讓結果更加嚴謹，且擁有更高的真實性[7]。亦可實現投入課堂講學的使用，通過實際的操作讓學生們更好地理解相關知識，提升課堂效率和提高課堂質量。