用于振蕩水柱波能系統的徑流式空氣透平數值模擬研究

楊 鑫，劉 臻，張曉霞

(中國海洋大學 工程學院，山東 青島 266100)

隨著社會的發展，人類活動對環境的影響、能源安全和可持續發展等矛盾一直是世界各地許多國家和組織議程的首要問題。歐盟、中國、美國等[1-6]全球能源市場的主要參與者更是越來越重視這些問題，他們所制定的政策與發展方針正在推動以清潔的可再生能源為主導的能源轉型進程，使可再生能源可以作為化石燃料的可靠替代品。海洋可再生能源是幾乎未被開發的清潔能源，具有極高的可用性，其估計儲量大約為151 300 TWh/A，其量級與世界對一次能源的需求量相當[7]。

在許多國家，尤其是歐洲和亞洲國家，波浪能被認為是一種豐富而有前途的可再生能源[8-9]。在各種各樣的波浪能系統轉換裝置中，振蕩水柱波能轉換系統被認為是用于捕獲波浪能的最常用裝置，因為其可與沉箱防波堤相結合，且除透平外無其他可活動機械部件，因此安裝成本低且維護方便。其中可以轉化為可用能量的大小，在很大程度上取決于氣室內部和空氣透平內部的流動特性，這些流動用于將氣動能轉換為機械能。作為振蕩水柱波能轉換系統的二級能量轉換裝置，空氣透平主要包括軸流式、徑流式兩種類別，其中徑流式空氣透平的徑向配置能明顯降低其軸向推力，且具有較低的制造成本和較高的扭矩輸出[10]，因此關于徑流式透平的研究也得到越來越多的重視。Setoguchi等[11]用試驗的方式研究了導流葉片角度對徑流式透平特性的影響，并建議將25°作為內、外側導流葉片的最佳選擇；Pereiras等[12]分析了轉子尖端間隙、內側導流葉片和外側導流葉片對該透平性能的影響，觀察到葉尖間隙效應在透平內部流速較高的區域更為明顯；Elatife等[13]對徑流式透平進行了進一步的優化，成功的使用試驗設計(DOE)方法分析了10個幾何參數對透平性能的影響，研究發現轉子葉片對透平效率的影響最大，尤其是葉片安裝角，當交錯角為4°時透平在吸氣與呼氣階段均能保持較高的效率，其效率提高了19%；Ansarifard等[14]利用9個設計變量控制轉子的形狀及調整氣流向內流動方向，通過使用非對稱的葉片，發現優化的轉子可實現較高的輸出功率，同時優化了下游部分，以便與優化的流入轉子有效匹配，并使用4個參數控制下游部分的形狀，結果表明優化后的透平在吸氣模式下的穩態峰值效率可達81%；Falcao等[15-16]和Gato等[17]介紹了一種新型的徑流式自整流透平，該透平結構較為復雜，但是峰值效率卻能達到80%以上。其他大多數研究也都集中在透平的轉子及導流葉片。由此可見，轉子及導流葉片對透平性能影響極其重大。

目前對徑流式空氣透平的研究均是對轉子葉片及導流葉片結構和安裝角度進行探索，還沒有對葉片數量的影響進行研究。針對這一問題，將展開不同轉子葉片稠度對透平性能影響的研究。

1 研究內容

1.1 研究方法

在對透平運行特性的研究中，其動力輸入條件及工作性能評價均包含定常與非定常兩個概念。若入射氣流的大小、方向均不隨時間發生變化，則稱為定常氣流條件，反之稱為非定常氣流條件；若透平的扭矩、壓強、轉速等輸出物理量均不隨時間發生變化，則稱為定常工作狀態，此時透平展現出定常工作性能，反之稱為非定常工作狀態，此時透平展現出非定常工作性能。雖然在實際海況下流經透平的氣流是不規則、非定常的，但是將氣流條件簡化為定常氣流是對實際問題的合理簡化，有助于揭示透平的基本工作原理并優化其結構形式，是一種研究透平的高效手段。

通過應用機械設計軟件Solidworks15.0及商業計算流體力學(CFD)軟件Fluent實現數值模擬計算。徑流式空氣透平結構復雜，因此利用專業機械設計軟件Solidworks15.0進行幾何建模；隨后采用ICEM實現透平網格劃分，為保證計算精度及減少計算時長，在全流域采用結構化網格；最后利用Fluent16.0進行數值計算。Fluent基于有限體積法求解Navier-Stokes方程，流動模型通過使用分離的求解器來求解不可壓縮的流體守恒方程，其中擴散項采用中心差分格式進行離散，對流項采用二階精度迎風格式進行離散，壓力—速度耦合通過SIMPLE算法執行。在湍流模型的選擇時，參考已有數值研究經驗[18]，使用realizable k-ε湍流模型與標準壁函數。相比于非定常數值計算，定常數值計算能夠在保證結果可靠性的同時，大大縮短計算運行時間，充分提高研究效率。因此，所有數值計算均在定常條件下進行。

1.2 幾何模型

文中主要研究用于振蕩水柱波能裝置的徑流式空氣透平，徑流式透平的軸向進/出口連接到氣室出口，如圖1所示，其中轉子與內、外側導流葉片均等距分布。該透平主要參數如表1～3所示。

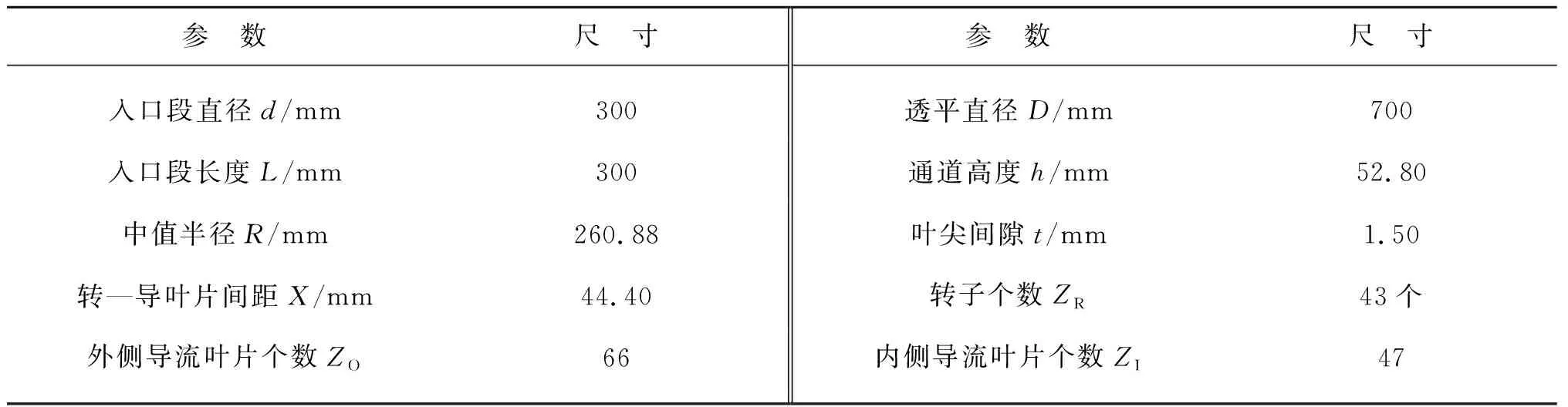
表1 透平規格Tab. 1 Specifications of radial turbine

圖1 徑流式透平結構示意Fig. 1 Schematic of radial turbine

轉子葉片是透平直接提取能量的結構，除轉子葉片結構外，合理配置轉子葉片個數與弦長也是保證透平正常運行的關鍵因素，目前，常用稠度來描述透平轉子葉片個數，稠度σ是表征透平葉片個數的無量綱數，其與葉片個數ZR、葉片弦長lR、透平中值半徑R的關系為：

(1)

此次研究將選用5種不同的轉子葉片稠度來討論其對透平工作性能的影響，在實物裝置轉子稠度1.70的上下進行稠度選擇，稠度分別為σ=1.38、1.70、2.02、2.34、2.65，其對應的轉子葉片個數分別為：ZR=35、43、51、59、67。

表2 轉子葉片規格Tab. 2 Specifications of rotor

表3 導流葉片規格Tab. 3 Specifications of guide vane

1.3 網格劃分

研究借助ICEM實現三維結構化網格的構建，具體網格劃分如圖2所示。研究只針對振蕩水柱波能系統的二級能量轉換裝置空氣透平，因此忽略氣室對透平的影響，并對透平進行合理簡化。

圖2 網格示意Fig. 2 Schematic of mesh

徑流式空氣透平中僅轉子旋轉，其內、外側導流葉片均不旋轉，因此需將整個計算域劃分為幾個不同區域：旋轉的轉子葉片區域，靜止的內、外側導流葉片區域以及入口區域。其中，不同子區域之間的數據傳遞通過Interface實現。透平轉子區域可相對內、外側導流葉片旋轉以模擬轉子定轉速運動。此外，在不同區域的交界面、轉子葉片及導流葉片處的網格分布較為緊密，這是由于葉片周圍的流場較為復雜，需要加密網格保證計算精度。最后利用多參考系模型實現透平定轉速運動的模擬。

2 研究結果

透平運行特性的計算結果用扭矩系數CT、輸入系數CA和效率η表示，它們均與流量系數φ相關，其定義如下[11]：

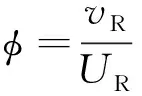
(2)

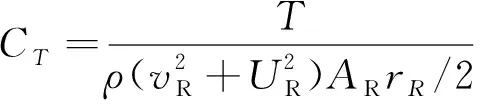
(3)

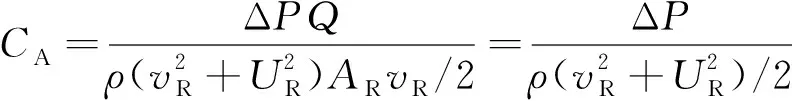
(4)

(5)

式中：ΔP為透平入口與出口兩端的壓降；T為透平輸出扭矩、Q為氣流流量；AR表示中值半徑處的截面面積；vR表示中值半徑處的徑向流速，UR表示轉子圓周速度。AR、vR與UR可分別定義為：

AR=2πrRh

(6)

(7)

UR=ωrR

(8)

2.1 模型驗證

由于計算將在全流域進行，并非采用周期邊界條件，因此模型網格數對計算時長及結果影響較大，因此首先開展了基于物理模型試驗數據的網格無關性驗證。

試驗平臺示意如圖3所示，整體可分為3部分：定常風洞、透平、數據采集及控制系統。定常風洞實物如圖4(a)所示，可造出試驗所需的穩定入射氣流。裝置及后端數據采集系統如圖4(b)所示。透平結構尺寸如1.2節所述，其中轉子葉片稠度為1.70；數據采集系統主要包括壓差變送器、電磁離合器、扭矩傳感器、伺服電機、數據采集箱等，其主要作用為實時采集試驗過程中氣壓、透平輸出扭矩、透平轉速等關鍵物理量，控制透平啟停及轉速。試驗時，定常風洞給定穩定的5 m/s定常入射流速，通過電磁離合器及伺服電機控制透平的啟停并將透平轉動后的轉速穩定在不同轉速，根據式(2)獲得不同的流量系數，利用壓差變送器、扭矩傳感器采集到的實時物理量根據式(3)～(5)計算出透平輸出效率，為透平數值模型驗證提供數據支持。

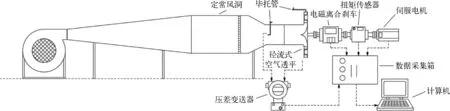
圖3 試驗平臺示意Fig. 3 Schematic diagram of test platform

圖4 試驗平臺實物Fig. 4 Physical map of test platform

相同結構尺寸下，選取轉子葉片稠度同樣為1.70的數值模型，采用realizable k-ε湍流模型，在與模型試驗相同工況下進行數值計算，將3.0×106、3.9×106以及5.3×106三種網格數量下的數值計算結果與該裝置試驗結果進行對比，結果如圖5所示。其中，橫坐標為流量系數φ，縱坐標為透平定常輸出效率η。綜合考慮計算時耗及精度，數值模擬研究確定網格數約為3.9×106。

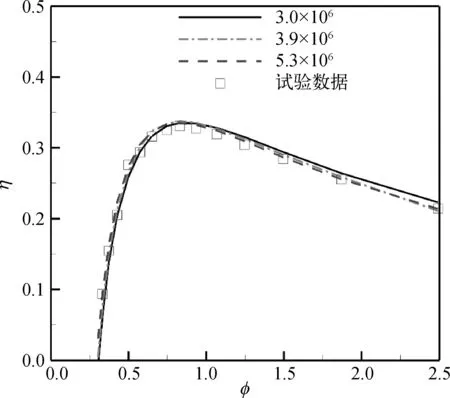
圖5 網格數對透平效率的影響Fig. 5 The effect of grid number on turbine efficiency

2.2 數值計算結果分析

計算中所有工況的入射流速大小均為5 m/s，通過給定不同轉速以獲得不同流量系數下透平運行特性。在實際海況下，流經透平的氣流為雙向往復氣流，因此，在數值計算時給定入口流速為5 m/s(正向氣流)和-5 m/s(反向氣流)兩種流速，以探索不同氣流流向下轉子葉片稠度對透平定常工作性能的影響。在保證透平其他尺寸、參數不變的情況下，通過對比轉子葉片附近的速度分布及透平定常性能評價參數隨流量系數的變化規律來考察轉子葉片稠度對透平工作性能的影響。

理論上，對于透平機械的葉片，存在一個可使總損失達到最小的最佳葉片數目(或葉片稠度)。在一定輪軸半徑下，若轉子葉片稠度過大，透平內的氣流流道則會被壓縮，轉子葉片對流體的導向作用增大，但同時摩擦損失也會變大；反之，透平內氣流流道較寬，轉子葉片對流體的導向作用較差，由流動分離造成的損失會較高。

圖6給出了4種典型工況下轉子附近速度云圖，4種工況為兩種入口流速(5 m/s和-5 m/s)及兩種轉子葉片稠度(1.70和2.34)兩兩組合形成，4種工況對應的流量系數均為0.83，即正向氣流下轉子稠度為1.70的透平輸出峰值效率對應的流量系數。圖6中箭頭表示氣流方向。如圖6(a)所示，氣流從下至上流動，在葉片吸力面迎流端發生流動分離，一部分氣流沿著吸力面加速流動，并在轉子葉片中部形成高流速區，另一部分氣流則越過迎流端在壓力面發生明顯的流動分離現象，并且氣流經過葉片中部后與葉片尾部貼合情況并不理想；同時，動葉片吸力面尾端也出現了較大程度的流動分離現象。如圖6(c)所示，當葉片稠度增加到2.34時，轉子葉片附近流域的寬度減小，轉子葉片對流體的導向作用增強，具體表現為：吸力面中部高流速區的峰值及覆蓋面積增大；壓力面流速分離受到明顯抑制；氣流流經轉子葉片中部后更加貼合葉片尾端流動。當氣流為反向流動時，即如圖6(b)所示，氣流從上至下流動，在轉子迎流側并未發生明顯的流動分離，一部分氣流沿著吸力面加速流動，并在轉子葉片中部形成高流速區，但氣流在葉片后半段出現了明顯的流動分離，使得透平損失增加。如圖6(d)所示，當稠度增加到2.34時，氣流在吸力面形成的高流速區擴大，且氣流流經轉子葉片中部后更加貼合葉片尾端流動。對比圖6(a)、(b)及圖6(c)、(d)發現，雖然徑流式透平可在雙向氣流下實現單向旋轉，但是透平在不同流向氣流下所表現出的特性存在較為明顯的差異，這與傳統的軸流式透平有很大不同，因此在分析透平定常性能時，需同時研究徑流式透平在不同流向氣流下的工作性能。

圖6 轉子葉片稠度對葉片附近速度云圖的影響(φ=0.83)Fig. 6 The influence of the consistency of the rotor blade on the speed cloud near the blade (φ=0.83)

圖7給出了不同轉子稠度下透平各定常評價參數隨流量系數φ的變化規律,圖中橫坐標為流量系數φ，φ>0表示透平在正向氣流下工作，即入口流速為5 m/s，φ<0表示透平在反向氣流下工作，即入口流速為-5 m/s。如圖7(a)所示，當氣流流向為正向時，在低葉片稠度下葉片稠度對輸入系數的影響并不明顯，圖中σ=1.38與σ=1.70對應下的輸入系數變化曲線幾乎重合；但是當σ>1.70后稠度對輸入系數的影響較為明顯，隨著轉子葉片的稠度增加，在整個流量系數范圍內輸入系數越大，并且輸入系數增大幅度隨著流量系數的增大展現的更為明顯。當輸入氣流為反向氣流時，σ=1.38、σ=1.70及σ=2.02對應下的輸入系數變化曲線幾乎重合；當σ>2.02后稠度對輸入系數的影響規律與正向氣流下相同。

圖7(b)為不同轉子稠度下透平扭矩系數隨流量系數φ的變化規律，整體上，在整個流量系數范圍內，扭矩系數隨轉子稠度的增大而增大。當氣流方向為正向時，σ>1.70時扭矩系數的增大幅度明顯大于σ<1.70，但當氣流方向為反向時，扭矩系數隨稠度增加的幅度幾乎相同。

圖7(c)為不同轉子稠度下透平輸出效率隨流量系數φ的變化規律。稠度對透平效率的影響在整個流量系數范圍內均較為明顯。當氣流方向為正向時，透平峰值效率隨著流量系數的增加呈現出先升后降的趨勢，其拐點出現在σ=2.34處，此時透平峰值效率最大。然而，稠度對整個流量系數范圍內透平效率的影響規律并不同于對峰值效率的影響。在大流量系數下，尤其是在φ>2.0時，雖然透平輸出效率隨著稠度的增加同樣呈現出先增后降的趨勢，但其拐點則出現在σ=2.02處。當σ=2.65時，大流量系數下的透平效率隨稠度的增加下降極為明顯；當φ<0.5時，透平效率始終隨著稠度的增加同樣呈現出先增后降的趨勢，尚未出現拐點。當氣流方向為反向時，透平峰值效率隨轉子葉片稠度的變化規律與正向氣流相似，其峰值效率的拐點同樣出現在σ=2.34處。

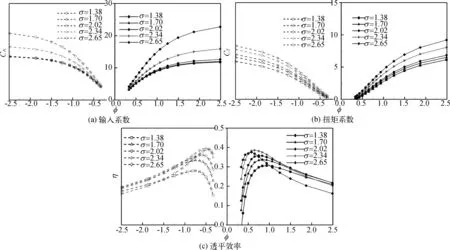
圖7 轉子葉片稠度對透平性能的影響Fig. 7 The influence of the consistency of the rotor blade on turbine performance

表4為不同轉子葉片稠度對透平輸出峰值效率的影響，從圖7中還可看出：1)峰值效率隨著轉子葉片稠度的增加有明顯的先升后降的趨勢，不同流向下透平輸出峰值效率拐點均出現在σ=2.34處。當入射氣流為正向時，最大峰值效率為38.6%，當入射氣流為反向時，最大峰值效率為39.7%；2)隨著轉子稠度的增加，透平峰值效率所對應的流量系數逐漸減小。以正向氣流為例，當σ=1.38時透平峰值效率出現在φ=0.83處，但當σ=2.65時，透平峰值效率則出現在φ=0.57處；3)當入射氣流方向發生變化時，即使流速大小相同，峰值效率對應的流量系數也存在偏差。以σ=2.34為例，正向氣流下峰值效率出現在φ=0.65，而反向氣流下峰值效率出現在φ=0.50。

表4 不同轉子葉片稠度對峰值效率的影響Tab. 4 The influence of different rotor blade consistencies on peak efficiency

綜上所述，在輪軸半徑相同條件下，綜合考慮正向、反向氣流下透平在整個流量系數范圍內輸出效率，透平在σ=2.34時的工作性能最優。

3 結 語

通過定常數值計算，在不同氣流流向下探索了不同轉子葉片稠度對徑流式空氣透平工作特性的影響規律。研究結果表明：1)雖然徑流式透平可在雙向氣流下實現單向旋轉，但當氣流方向不同時，透平展現出的定常工作性能存在明顯差異，其差異主要包括轉子葉片周圍的流場，輸入系數、扭矩系數隨轉子葉片稠度的變化趨勢，輸出效率的峰值及對應的流量系數；2)稠度對透平效率的影響在不同流量系數范圍內也同樣存在差異，在大流量系數下透平輸出效率隨稠度的增加先升后降，而在小流量系數下，尤其是在φ<0.5時，透平輸出效率隨著稠度的增加而增加，尚未出現拐點。因此，綜合考慮氣流流向、透平整個工作范圍內輸出效率，在輪軸半徑相同條件下，當轉子葉片稠度為2.34時透平定常工作性能最優。