基于Usui模型的往復活塞桿密封圈磨損仿真研究

蔡少波 閔林鋒

（溫州職業技術學院瑞安學院）

往復式活塞桿的做功往往是通過液壓結構來進行的，而在做功過程中密封裝置會與運動零件相互接觸，直接影響結構的密封壽命［1～3］，需要在往復活塞桿上添加密封圈以對液壓進行輔助密封，也可作為運動零件和主要密封裝置之間的緩沖結構［4，5］。 但由于密封圈的特殊作用，工作過程中往往會出現較大的磨損。 為了在設計階段就得出密封圈在實際使用時的磨損情況，通常選擇對密封圈進行磨損仿真［6～8］。對材料的磨損仿真研究中，國內外學者首先通過建立幾何和材料性能模型來進行仿真， 但該方法得不到動態結果，后有研究者通過有限元分析軟件進行動態仿真測試［9，10］，就目前的仿真結果來看，尚不理想。 經過分析后發現，當前的磨損仿真中缺乏對于材料自身應力應變反應的考慮，勢必造成仿真結果誤差較大。筆者針對該情況，提出基于Usui模型的往復活塞桿密封圈磨損仿真方法。

1 磨損仿真模型設計

1.1 Usui磨損模型

通常活塞在運行過程中，由于活塞桿的作用力往往會導致密封圈出現磨損現象［11］。 筆者采用Usui磨損模型作為密封圈的磨損模型， 首先采用最小能量法得出密封圈的磨損率， 其計算公式為：

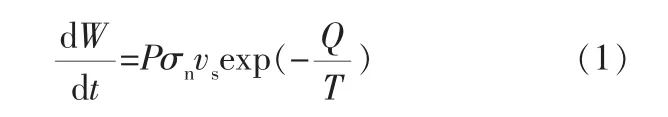
式中 dW/dt——密封圈的磨損率，mm/min；

P、Q——不確定常數；

T——活塞桿的工作溫度，℃；

vs——活塞桿相對于密封圈的滑移速度，mm/s；

σn——密封圈表面受到的摩擦應力，MPa。

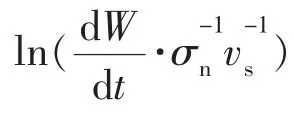
結合文獻［13］，基于Archard模型，對密封圈的磨損情況進行分析，運動副材料的磨損體積dV為：

式中 dL——運動條件下運動副表面相對移動距離；

F——活塞運動副中的法向力；

H——活塞運動副中的密封圈硬度；

K——無量綱下的運動磨損率。

將式（2）的兩端除以密封圈的磨損面積，則可得到密封圈材料磨損高度dh：

式中 Kh——磨損率與密封圈硬度的比值，Kh=；

p——材料運動副中的正壓力。

活塞實際的運動過程中， 由于壓力p是隨時間變化而改變的量，當運動副處于勻速運動狀態時，可將式（3）改寫為：

式中 p（t）——隨時間變化的壓力值。

至此，完成磨損模型的建立，進而確定相應的參數，并將模型導入至有限元分析軟件中。

1.2 密封圈材料的應力應變確定

通常條件下，密封圈材料為橡膠，但根據不同活塞桿的需求，不同類型的密封圈橡膠性能差別較大，而不同密封圈材料的應力應變性能也對磨損影響較大，因而密封圈材料中的應變矢量{ε}可按下式［14］確定：

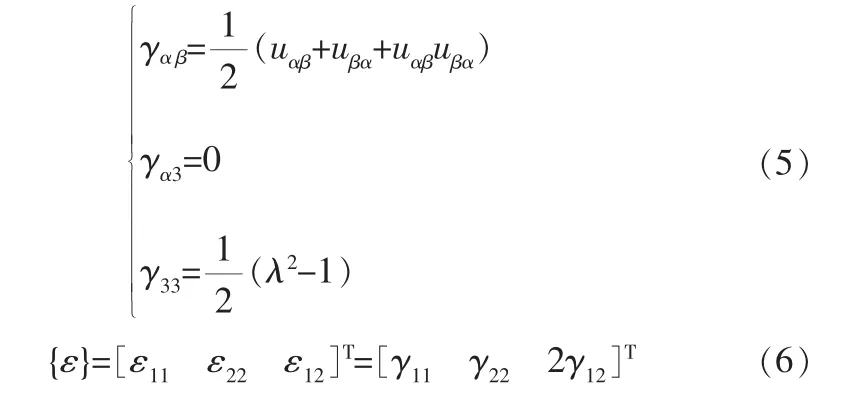
式中 uαβ、uβα——密封圈材料的位移分量，α、β可取1、2；

γαβ——密封圈材料的應變張量，α、β可取1、2；

ε——密封圈材料的物理分量；

λ——密封圈材料的伸長率；

下角1、2、3——x方向、y方向、z方向。

設位移分量變換按下式變化：

其中i、j可取α、β。 將式（7）代入式（5）、（6）中，得出εij+Δεij，用{Δε}代表應變增量，并用增量的線性部分{Δξ}和非線性部分{Δη}來表示，即{Δε}={Δξ}+{Δη}，其中{Δξ}和{Δη}計算方法分別為：

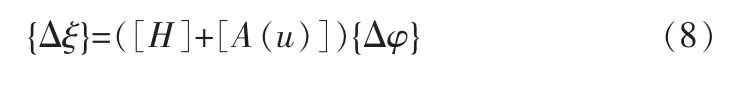
1.3 活塞桿紋理摩擦

在實際的制造中， 活塞桿是由機床車削制造， 因此在活塞桿外表面會存在車削刀具紋理，而紋理由峰和谷組成，當活塞運動時，密封圈的內表面會與 這些紋 理接觸產生 磨損［15，16］，因此采用正弦函數來定義活塞桿的峰谷紋理形貌，即活塞桿表面紋理與平衡位置的相對距離z（x）為：

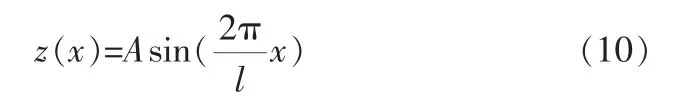
式中 A——表面紋理與平衡位置間相對距離的最大值；

l——車削過程中的進給量。

假設密封圈表面為純平面， 其泊松比為0.5，當作超彈性材料。 由于密封圈的彈性模量低于活塞桿，因此需要對密封圈的求解域選擇超彈性體單元，本構方程則為：

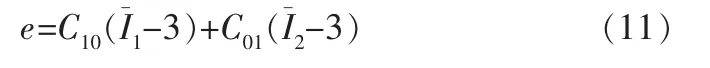
式中 C10、C01——密封圈的Rivlin參數；

e——活塞桿的應變能密度；

有限元分析軟件中導入式（10）、（11），以確定當前活塞桿的表面紋理峰谷狀態和表面超彈性體單元狀態。

2 磨損有限元仿真

有限元分析過程中導入上述計算公式的同時需考慮活塞桿長時間做功，高溫高壓往往會影響密封圈的磨損。 因此，有限元分析時將初始溫度設為95～135 ℃，同時根據相應的摩擦力和運行速度，添加溫度的變化曲線。 同時將作用在密封圈表面的壓力設為6.0～8.5 MPa。

筆者采用Abaqus有限元分析軟件來進行密封圈的有限元接觸分析，并在密封圈和活塞桿的接觸區域進行網格細化。 對于活塞桿的表面則采用z（x）進行模擬，同時在密封圈的求解域上添加流體壓力來表示其中的邊界條件。 分析時，首先對運動狀態施加z方向負位移作為預變形的模擬，同時將其中的密封圈截面直徑進行壓縮，密封圈截面直徑為4.75 mm， 模擬中將壓縮率設為35%，并使運動腔體沿z軸向下的位移為0.831 25 mm；然后開始模擬密封圈的磨損過程，并將軟件中的活塞桿x軸正負方向做功，同時在往復運動下，使活塞桿保持一定的運動周期（圖1），作為仿真運動的狀態。

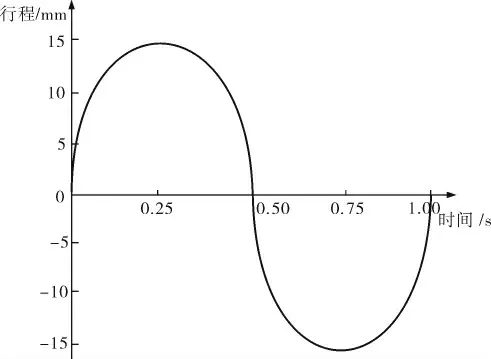
圖1 活塞桿運動位移周期示意圖

模擬開始時，根據上述設定，在軟件中輸入密封圈的材料參數和幾何參數，同時添加活塞桿的相關參數，并模擬周期性運動，而對單元應力的判斷則需要判斷是否超過設定的閾值，即單元i的應力σi數值超過設定的閾值σmax， 就將單元i消隱。 在仿真模擬過程中，個別單元往往會由于活塞桿的過度做功導致變形（圖2）。 為了保證仿真的順利進行，筆者在其中添加了過濾器來檢查仿真中的單元變形。

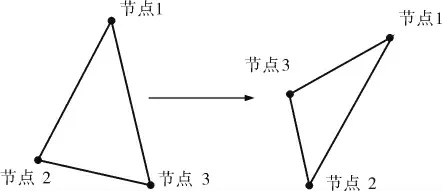
圖2 單元變形示意圖

在圖2中，將單元添加節點1、2、3組成單元初始法向量Vp0，而發生扭曲變形后的法向量則為Vp1， 同時定義各節點的坐標位置 （xi，yi，zi）（i=1，2，3），對應的Vp0和Vp1就可以表示成：

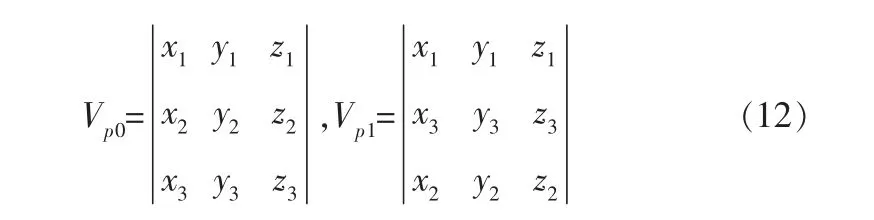
通過坐標位置的變化來判斷單元的變形狀態。

3 仿真參數設定

3.1 模擬參數

實驗中采用O形密封圈， 該密封圈內徑為74.8 mm，密封圈截面直徑為4.75 mm，保護溝槽內徑為74.17 mm。活塞桿工作下的油壓為20.5 MPa，密封圈材料采用丁腈橡膠，橡膠的熱膨脹系數為5.82×10-4℃-1，實驗中的活塞桿采用56號鋼制作，其導熱系數為42.7 W/（m·K），摩擦副間的摩擦系數為0.27。 所創建的三維模型如圖3所示，參考活塞桿與密封圈實際安裝位置確定其配合關系。 如圖4所示， 密封圈采用0.4 mm的六面體C3D8H網格劃分，壁面和活塞桿采用六面體C3D8網格漸變劃分，從接觸位置到外部逐步由0.4 mm增長至1.0 mm和2.0 mm，最終擴大至4.0 mm，在保證計算精度的情況下，盡量減少計算時間。 最后，設置材料參數和固定外圈邊界， 并按圖1位移周期設定活塞桿運動規律，加載進行計算。

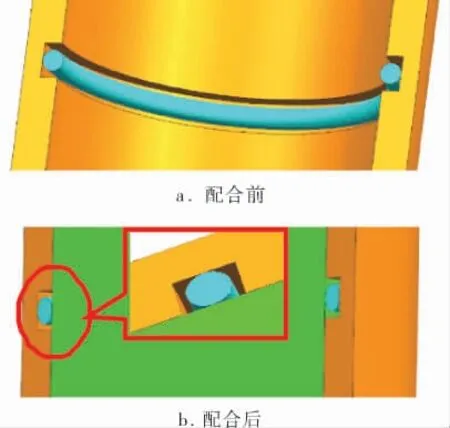
圖3 活塞桿密封圈配合狀態的三維模型

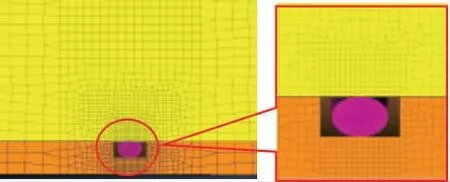
圖4 有限元網格劃分

3.2 工況參數

磨損仿真實驗按4種不同的工況進行， 工況參數見表1。

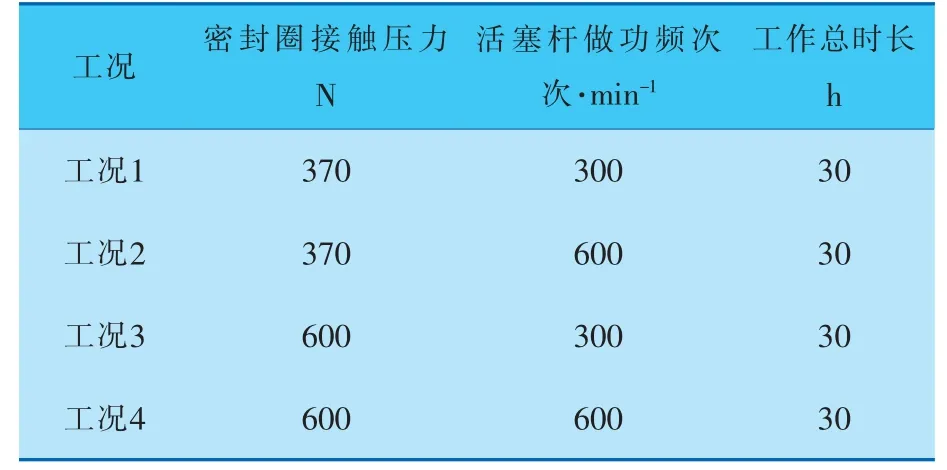
表1 仿真活塞桿工況參數

在仿真實驗和實際運行中， 在24 h的工作總時長中，為避免過熱，每5 h的做功后便有1 h散熱停工。

4 仿真結果分析

為了驗證筆者設計的磨損仿真方法的可行性， 采用某型號的往復式活塞桿作為仿真對象，以基于筆者設計（基于Usui模型且考慮峰谷紋理）的仿真方法為方法1，以基于Usui模型且紋理光滑的仿真方法為方法2， 以基于Archard模型且考慮峰谷紋理的仿真方法為方法3， 以基于Archard模型且紋理光滑的仿真方法為方法4， 進行仿真實驗， 并與實際活塞桿密封圈的磨損狀況進行對比，判斷4種仿真方法的性能。

4.1 工況1密封圈磨損仿真

工況1條件下密封圈磨損仿真結果見表2。

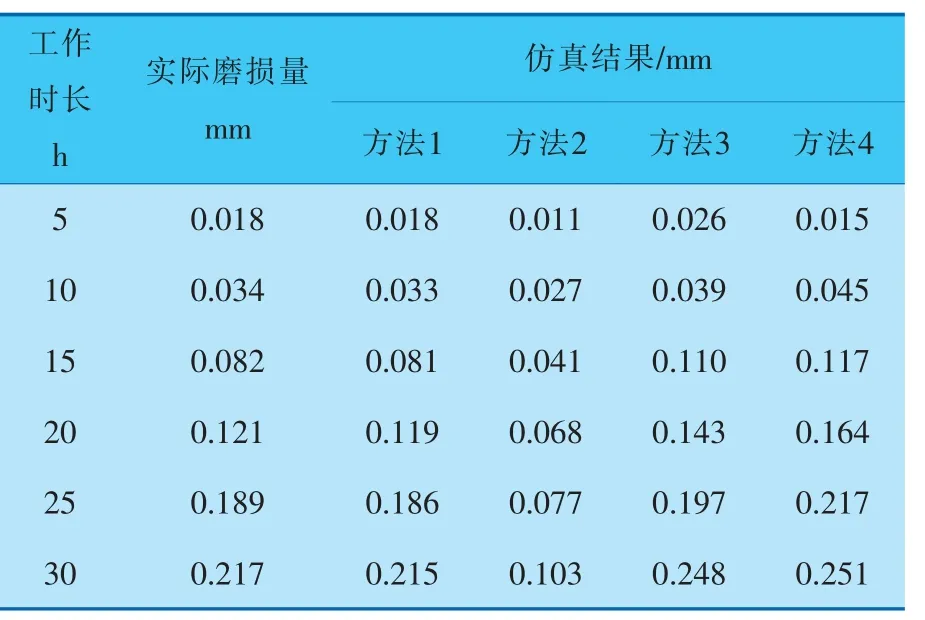
表2 工況1密封圈磨損仿真結果

由表2可知，方法1的密封圈磨損仿真結果比其他仿真方法的結果更接近實際磨損量。

4.2 工況2密封圈磨損仿真

工況2條件下密封圈磨損仿真結果見表3。

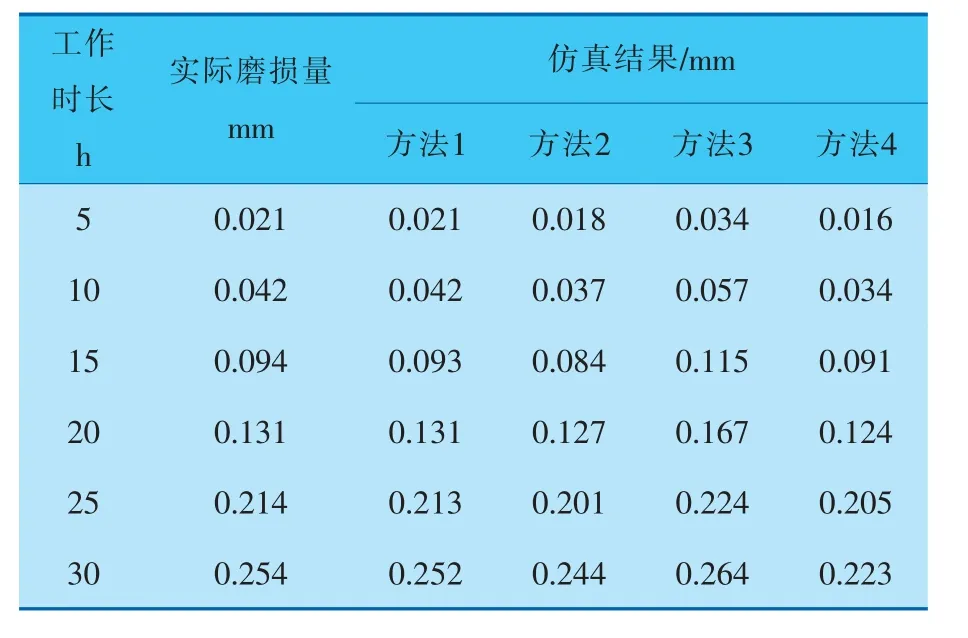
表3 工況2密封圈磨損仿真結果

由表3可知，方法1仿真結果更接近于實際工況下的磨損量，而方法2、方法3和方法4的仿真結果都低于實際磨損量，這可能是因為這些仿真方法中錯誤確定應力應變的增幅系數而導致的。

4.3 工況3密封圈磨損仿真

工況3條件下密封圈磨損仿真結果見表4。

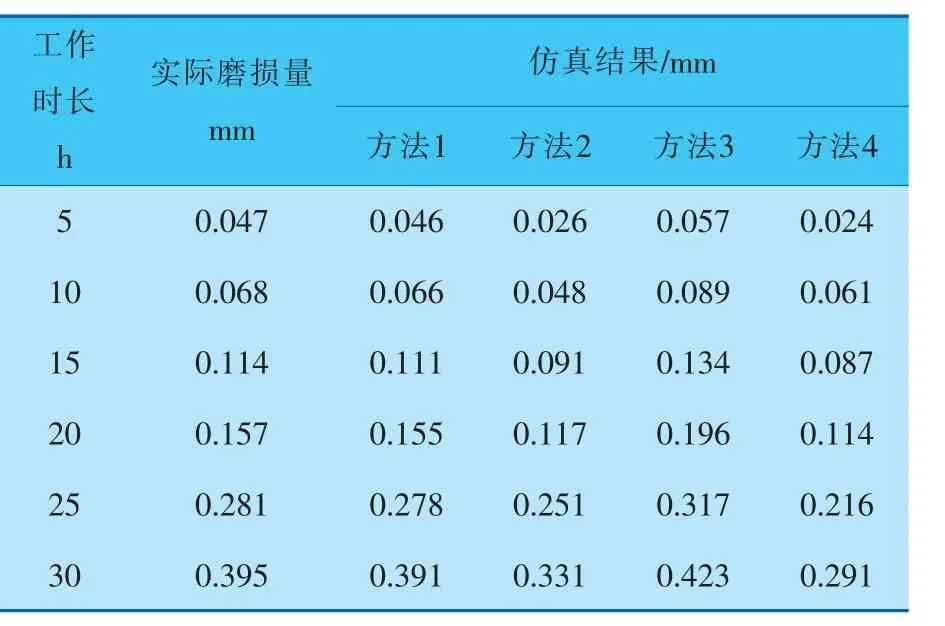
表4 工況3密封圈磨損仿真結果

由表4可知，方法1的仿真結果與實際磨損量的誤差開始增大， 且大于表2和表3中相應的誤差，這是由于密封圈接觸壓力過大，導致材料內部結構出現破損，磨損增加，影響了仿真結果。 但仿真結果相比其他方法誤差仍然較小。

4.4 工況4密封圈磨損仿真

工況4條件下密封圈磨損仿真結果見表5。

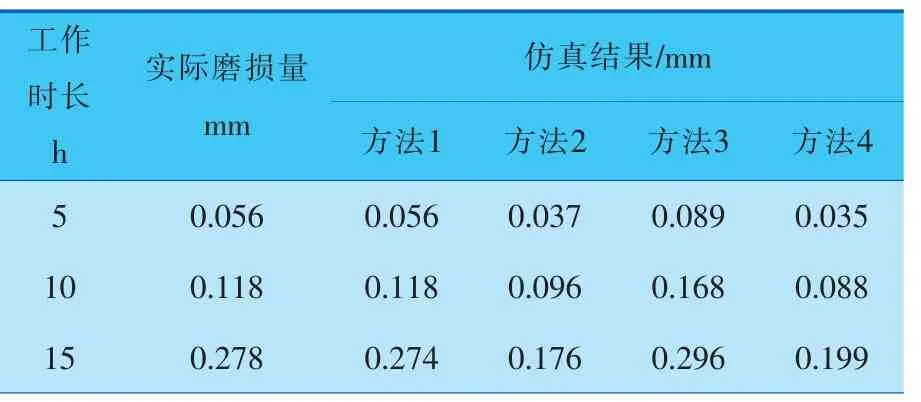
表5 工況4密封圈磨損仿真結果

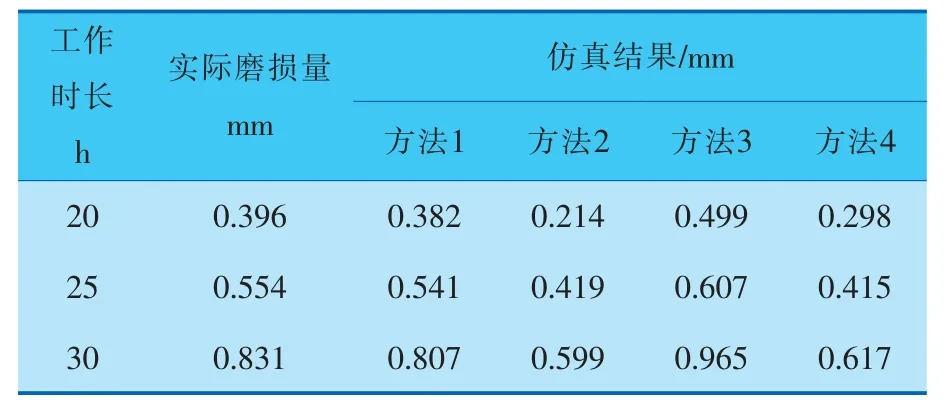
（續表5）

由表5可知，方法1在后續的仿真中，其結果與實際磨損量的誤差雖逐漸增大，但仍優于其他方法的結果。

5 結束語

筆者通過建立Usui模型， 并利用有限元分析軟件仿真活塞桿密封圈的磨損情況， 同時改進了材料的應力應變運算方法，經4種工況下的密封圈磨損仿真結果對比，該方法不僅具有可行性，而且準確性更高。 另外，在仿真實驗中的極端工況時，材料受到較大結構損壞，導致材料磨損增加時，仿真結果的誤差開始增大。 因此，在未來研究中，需要添加材料結構模型， 模擬材料內部結構的變化狀態，以進一步提高仿真結果的準確性。