基于偏最小二乘回歸的大壩安全監測數據缺失迭代修補方法研究

辛俊龍，葛 靜，朱斯楊，周子玉

(1.中電建電力檢修工程有限公司，四川 樂山 614000；2.中電建水電開發集團有限公司，四川 成都 610096；3.四川省遂寧市水利局，四川 遂寧 629000；4.四川大學 水力學與山區河流開發保護國家重點實驗室 水利水電學院，四川 成都 610065)

連續、完整、可靠的監測數據序列是大壩安全在線監控和運行性態評價的前提和基礎[1]。監測設備故障導致安全監測中斷、監測數據明顯錯誤被剔除未及時復測等，常造成安全監測數據序列的不連續，無法反映數據缺失時段的大壩運行性態，有必要對缺失時段的數據進行修補[2]。目前大壩安全監測缺失數據修補一般基于歷史監測數據序列，常見方法包括數學修補方法[3- 5]和考慮相關環境量影響的多元統計回歸模型修補方法[6- 8]。數學修補法較簡單，從歷時數據變化規律推測缺失時段的數據分布規律，當缺失數據較少時，數據修補精度較高，而缺失數據較多時，其修補精度較低。多元回歸模型在大壩安全監測缺失數據修補中應用最廣泛，能綜合考慮工程的結構特點、測值與環境量的相關關系等因素，該方法的缺失數據修補精度依賴于回歸模型本身的擬合精度，當模型復相關系數較低時，缺失數據修補精度一般較低。針對常用缺失數據修補方法在缺失比例高、模型擬合精度差等情況下精度較差的問題，本文基于偏最小二乘回歸基本原理，引入迭代修補思路，提出基于偏最小二乘回歸的缺失數據迭代修補方法，并結合實際工程，分析其適用性，校驗其修補精度。

1 基于偏最小二乘回歸的數據修補方法

1.1 基本原理

本文提出的數據缺失迭代修補方法基于偏最小二乘回歸模型，即將多元線性回歸分析、典型相關分析及主成分分析有機結合起來，其基本原理和方法如下：

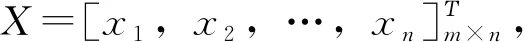
(1)數據預處理

對X，Y進行標準化得到自變量矩陣E0和因變量矩陣F0。

(2)自變量和因變量矩陣的主成分提取

首先提取因變量矩陣F0的主成分u1和自變量矩陣E0的主成分t1。根據主成分分析原理可知，為使提取出來的主成分t1和u1能最大程度的代表各自矩陣的數據變異信息且t1對u1的解釋能力最強，需要t1和u1各自的方差達到最大且相關程度達到最大，即：

Var(t1)→max，Var(u1)→maxr(u1，t1)→max

(1)

(2)

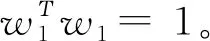
(3)

上述問題可通過SIMPLS算法[9]或NIPALS算法[10]來求解，求得w1后，即可得成分t1=E0w1。

(3)構建標準化變量的回歸方程

提取主成分t1=E0w1后，則E0、F0在t1上回歸為式(4)

(4)

式中，E1、F1—兩個回歸方程的殘差矩陣；p1、r1—回歸系數。

(5)

通過交叉有效性來判斷模型是否到達滿意的精度，如果沒有達到則對殘差矩陣提取主成分，過程和(2)類似：

(6)

(7)

式中，E2、F2—兩個回歸方程的殘差矩陣；p2、r2—回歸系數：

(8)

若模型未達到滿意的精度則需繼續提取主成分。假定共提取了k個主成分，得到標準化變量的回歸方程：

(9)

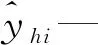
若當前主成分的加入不能明顯提升模型精度，則認為模型到達了滿意的精度，不再提取新的主成分。

(4)還原回歸方程

將標準化回歸系數還原為非標準化回歸系數，得到原始變量的回歸方程。

1.2 基本步驟

該方法基于偏最小二乘回歸，通過多次迭代回歸提升缺失數據修補精度，即首先構建原始數據序列的偏最小二乘回歸模型，獲取缺失時段的第一次數據修補值；再構建第一次數據修補后數據序列的偏最小二乘回歸模型，獲取缺失時段的第二次數據修補值，對比兩次修補值之間的差異，若差異小于控制值，則迭代結束，反之則重復迭代，其計算流程如圖1所示。

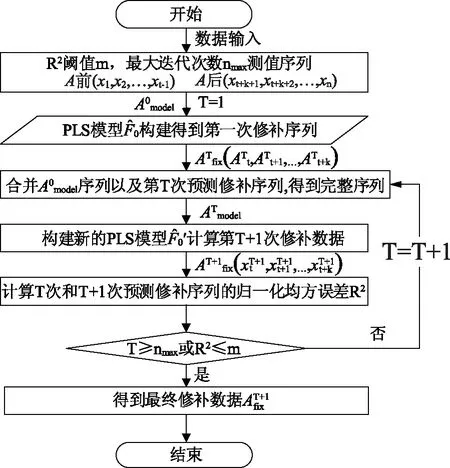
圖1 基于偏最小二乘回歸模型的數據修補方法流程圖

若存在一個監測序列A，其中包括n個測次的測值(x1，x2，…xn)，其數據缺測測次為(xt，xt+1，…xt+k)，則其缺測數據修補步驟如下：

①設置迭代控制值。迭代控制值可采用最大迭代次數nmax和R方預設閾值m。一般地，最大迭代次數nmax可設置為10，R方預設閾值m可設置為0.95。

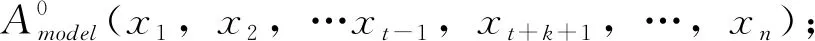
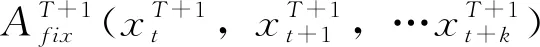
2 工程校驗與精度分析

2.1 精度分析

本文所提方法實質是基于迭代預測的偏最小二乘回歸改進模型，因此，主要與偏最小二乘回歸模型和逐步回歸模型對比，分析其數據修補精度。為具代表性，選擇大壩安全監測數據序列中最常見的周期型數據序列和直線型數據序列進行分析，數據缺失占比設置為10%。周期型監測數據序列以某壩心墻滲壓測點P94為例，采用2016年1月—2019年12月共798測次，將2018年7月19日—2018年12月7日共79測次的實測值作為缺失數據。直線型監測數據序列以某壩壩頂水平位移測點TP19為例，采用2014年2月—2019年2月共474測次，將2016年11月19日—2017年5月20日共47測次的實測值作為缺失數據。

經計算，不同方法的缺失數據修補效果見表1，修補效果對比如圖2所示。從圖表中可以發現，在缺失比例為10%時，本文所提方法對周期型數據序列的修補精度提升最為明顯，平均相對誤差分別較逐步回歸模型和偏最小二乘回歸降低61%和53%，R方提升46%和43%，對直線型數據序列而言，其修補精度較逐步回歸模型提升明顯，平均相對誤差降低43%，R方提升12%，較偏最小二乘回歸模型略有提升，平均相對誤差降低9%，R方提升6%。

圖2 三種方法數據修補效果對比圖

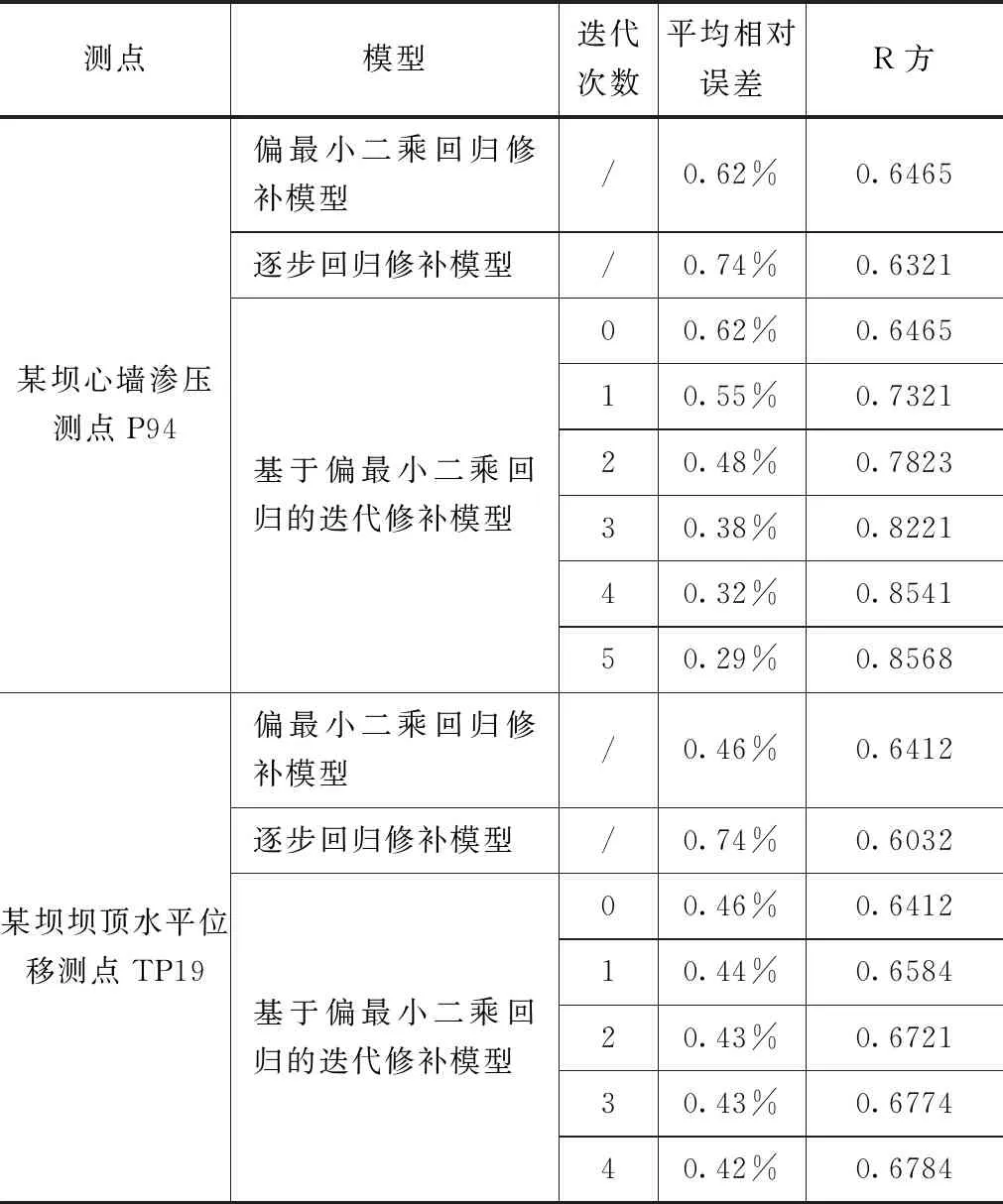
表1 兩種方法修補效果對比表

2.2 不同缺失比例的修補效果分析

為分析不同數據缺失比例下基于偏最小二乘回歸的數據缺失迭代修補方法的適用性，仍選擇周期型數據序列P94測點和直線型數據序列TP19測點，采用隨機設置缺失數據的方法進行分析，見表2。不同方法的數據修補精度對比如表3和圖3—4。

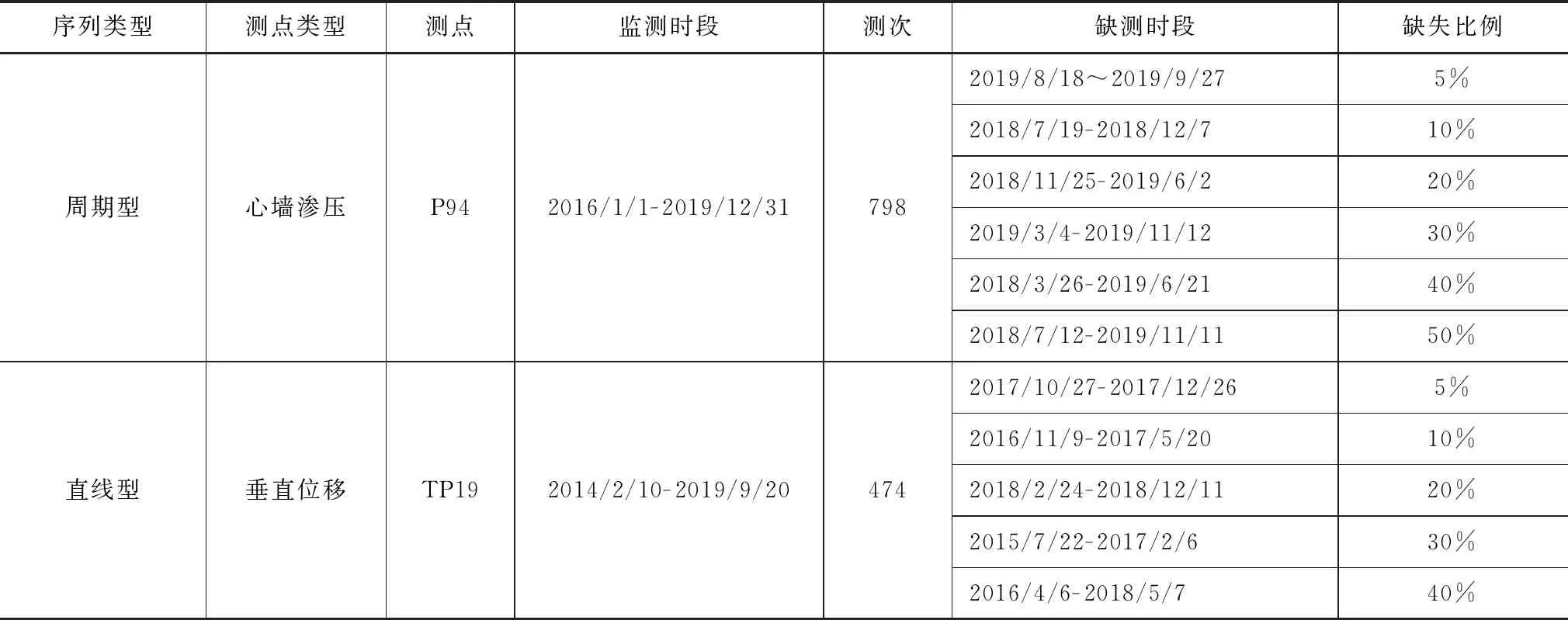
表2 不同缺失比例的對比方案表

表3 不同缺失比例下的修補精度對比表

從圖表中可以看出，不同缺測比例下，基于偏最小二乘回歸的數據缺失迭代修補方法的精度均明顯優于逐步回歸方法，特別是在數據缺失比例超過10%時尤其明顯。當缺失比例不超過20%時，兩種方法均有效，R方大于0.5，但數據缺失迭代修補方法較逐步回歸的平均相對誤差降低超過50%。當數據缺失比例超過30%時，逐步回歸法失效，R方低于0.5，而數據缺失迭代修補方法仍有效，特別是對周期型數據，當其缺失比例達到40%時，其R方仍大于0.5，滿足工程最低要求。

3 結語

(1)針對常用缺失數據修補方法在缺失比例高、模型擬合精度差等情況下精度較差的問題，本文以偏最小二乘回歸模型為基礎，引入迭代修補思路，提出了基于偏最小二乘回歸的缺失數據迭代修補方法，通過不斷迭代消除缺失數據的不利影響，有效提高模型預測精度和缺失數據修補精度。

(2)對比分析表明，缺失數據迭代修補方法較偏最小二乘回歸、逐步回歸等方法的缺失數據修補精度明顯提升，R方基本能提高至0.8以上，平均相對誤差降低約50%。

(3)工程校驗表明，缺失數據迭代修補方法對大壩安全監測常見的周期型和直線型數據序列修復的適用性較好，可修補的最大數據缺失比例由傳統的20%分別提升至40%和30%。

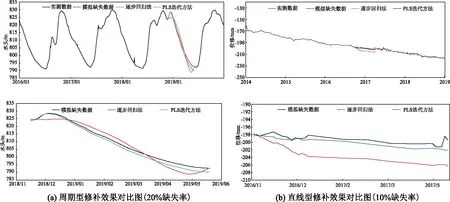
圖4 缺失比例不超過20%時缺失修補效果對比圖

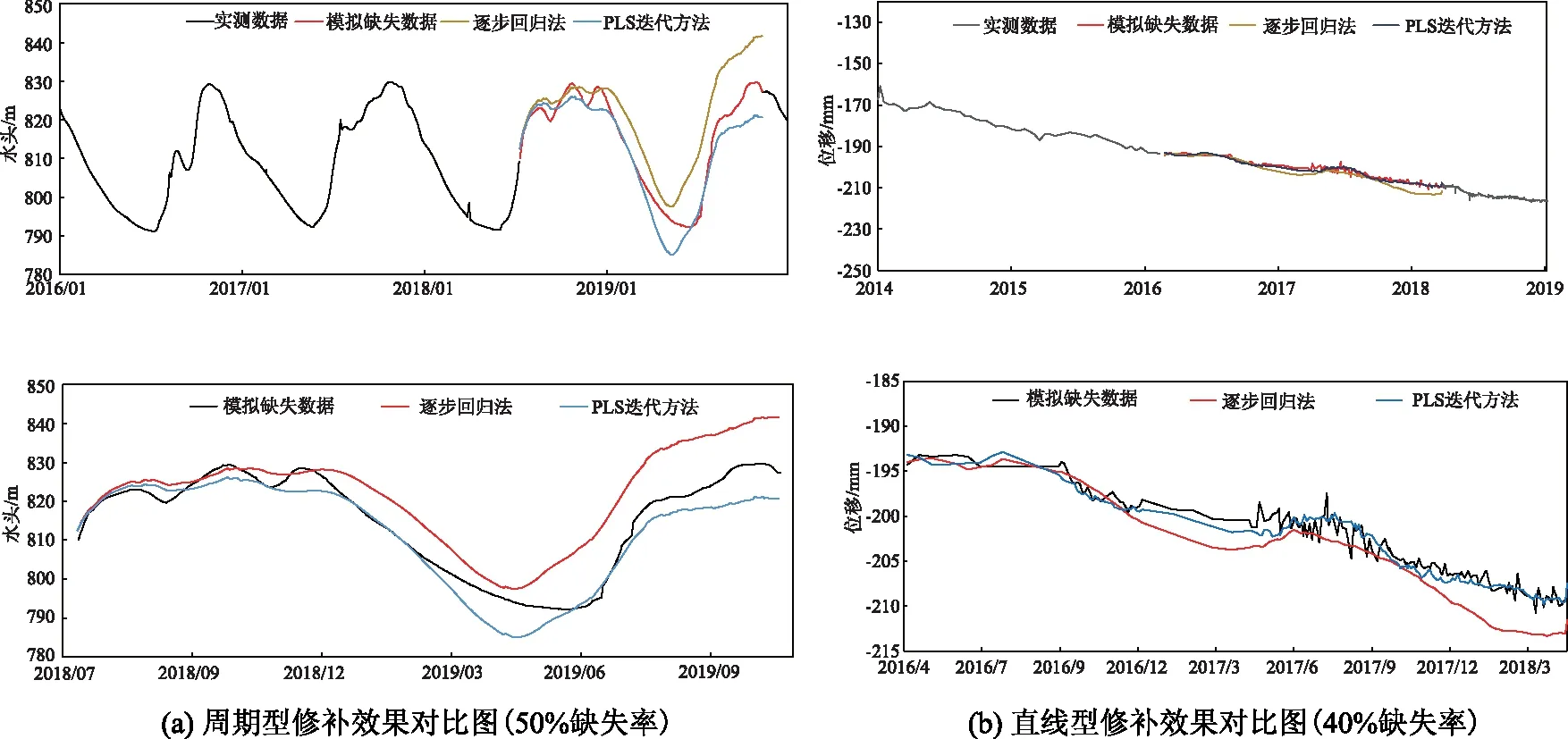
圖5 缺失比例超過20%時缺失修補效果對比圖