地下局部角度域高斯束偏移成像
黎孝璋 胡 林 任 婷 李 芳 魯統(tǒng)祥
(中海石油(中國(guó))有限公司海南分公司 海南海口 570312)
為了解決復(fù)雜介質(zhì)高精度成像問(wèn)題,地震偏移方法發(fā)展經(jīng)歷了從疊前時(shí)間偏移到疊前深度偏移[1-2]、從射線類偏移到波動(dòng)方程偏移[3-5]、從常規(guī)偏移到基于迭代反演的最小二乘偏移[6-7]。相較于常規(guī)射線類偏移方法,波動(dòng)方程偏移技術(shù)對(duì)于復(fù)雜構(gòu)造成像質(zhì)量有了較大提高,但是面對(duì)海量實(shí)際地震數(shù)據(jù),當(dāng)前計(jì)算機(jī)的計(jì)算能力還難以滿足大規(guī)模工業(yè)化地震處理需求,基于射線理論的常規(guī)偏移技術(shù)依然是工業(yè)化生產(chǎn)的主流選擇。受限于射線高頻近似假設(shè),常規(guī)射線類偏移技術(shù)對(duì)復(fù)雜構(gòu)造成像存在局限,如何提高射線類偏移技術(shù)對(duì)復(fù)雜構(gòu)造的成像精度一直是業(yè)界的重要研究方向。針對(duì)常規(guī)克希霍夫偏移無(wú)法適用于復(fù)雜構(gòu)造射線多路徑問(wèn)題,人們發(fā)展了高斯束偏移技術(shù)[8-10]。高斯束偏移不僅僅解決了射線多路徑問(wèn)題,較大程度提高了成像精度,最重要的是還保留了積分法偏移高計(jì)算效率的優(yōu)勢(shì),這點(diǎn)對(duì)于實(shí)際數(shù)據(jù)處理非常關(guān)鍵。但是在復(fù)雜構(gòu)造情況下,無(wú)論哪種射線偏移技術(shù),地面偏移距域射線偏移技術(shù)都會(huì)在偏移結(jié)果中產(chǎn)生運(yùn)動(dòng)學(xué)和動(dòng)力學(xué)假象[11],即使速度準(zhǔn)確,偏移距道集同相軸也并非拉平[12]。
針對(duì)上述問(wèn)題,很多學(xué)者提出了地下共成像點(diǎn)角度域射線偏移技術(shù)[13-15],在偏移過(guò)程中生成地下成像點(diǎn)角度域道集,而不是傳統(tǒng)射線偏移生成的偏移距道集。由于理論上反射系數(shù)為入射角的函數(shù),而不是偏移距的函數(shù),二者只有在簡(jiǎn)單層狀介質(zhì)情況下存在簡(jiǎn)單的函數(shù)關(guān)系,此外,地下局部角度域道集具有射線多路徑自適應(yīng)性,是唯一不存在假象的地震道集[16],因此地下成像點(diǎn)角度域道集更加適用于AVA分析及疊前反演。Xu等人[17]系統(tǒng)分析了地下共成像點(diǎn)角度域偏移對(duì)復(fù)雜構(gòu)造成像的優(yōu)勢(shì),并且從理論上指明了地面共炮域或者共偏移距域偏移不滿足成像條件的情況,而對(duì)于地下共成像點(diǎn)角度域偏移,絕大多數(shù)情況下反射波都滿足成像條件,因此偏移成像假象可以較好地被消除。
綜合上述偏移方法的優(yōu)缺點(diǎn),本文研究了一種地下局部角度域高斯束偏移方法,該方法具有計(jì)算效率高、成像精度高以及道集保幅性高的特點(diǎn),有效解決了復(fù)雜構(gòu)造成像多路徑以及真反射角偏移成像問(wèn)題。具體實(shí)現(xiàn)主要包括三個(gè)步驟:首先進(jìn)行地下成像點(diǎn)的射線追蹤及走時(shí)計(jì)算;然后求取地下成像點(diǎn)的局部反射角以在成像過(guò)程中對(duì)地震波場(chǎng)進(jìn)行角度域映射;最后應(yīng)用成像條件對(duì)數(shù)據(jù)進(jìn)行角度域射線束偏移成像。
1 高斯射線束偏移
炮域高斯束疊前深度偏移主要包括以下步驟:首先利用高斯束積分理論計(jì)算地下震源波場(chǎng);然后進(jìn)行傾斜疊加,將地震記錄分解為不同射線方向的波場(chǎng);最后利用高斯束積分理論將地震記錄反向延拓并應(yīng)用成像條件進(jìn)行成像。
二維介質(zhì)高斯束偏移通過(guò)高斯束積分求取格林函數(shù),震源坐標(biāo)為xs的地下任意一點(diǎn)x點(diǎn)波前高斯束積分表達(dá)式為
(1)
式(1)中:ω為角頻率;px與pz分別為震源入射射線初始慢度水平與垂直分量;uGB為入射高斯波束。利用動(dòng)力學(xué)射線追蹤計(jì)算高斯束的復(fù)值振幅A和走時(shí)T,上式可以表示為
(2)
高斯束是將波動(dòng)理論和射線理論結(jié)合起來(lái)的方法,同時(shí)進(jìn)行運(yùn)動(dòng)學(xué)和動(dòng)力學(xué)射線追蹤,然后根據(jù)所求的運(yùn)動(dòng)學(xué)和動(dòng)力學(xué)參數(shù)計(jì)算介質(zhì)任一點(diǎn)處的振幅和走時(shí),最后將每條高斯束的有效波束疊加起來(lái)得到地震波前。
地面地震記錄反向延拓公式為
U(x,xs,ω)=
(3)
式(3)中:U(x,xs,ω)為反向延拓的波場(chǎng);θr為地下成像點(diǎn)x到接收點(diǎn)xr處的射線出射角;vr為接收點(diǎn)處的速度;“*”代表復(fù)共軛;u(xr,xs,ω)表示檢波器及震源分別為xr、xs處的地震記錄。結(jié)合式(1),同時(shí)引入一個(gè)相位校正因子,考慮接收點(diǎn)附近高斯束反向延拓公式為
U(x,xs,ω)≈
(4)
式(4)中:ΔL為高斯束中心間隔;ωr為參考角頻率;ω0為初始高斯束寬度;θL、vL、pLx、pLz、TL分別表示以L為中心θ、v、px、pz、T對(duì)應(yīng)的變量;Ds(L,pLx,ω)為以L為中心的高斯窗內(nèi)地震疊加,表達(dá)為
(5)
最后應(yīng)用互相關(guān)成像條件即可實(shí)現(xiàn)高斯束偏移,互相關(guān)成像條件的格林函數(shù)表達(dá)為
(6)
2 成像條件
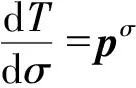
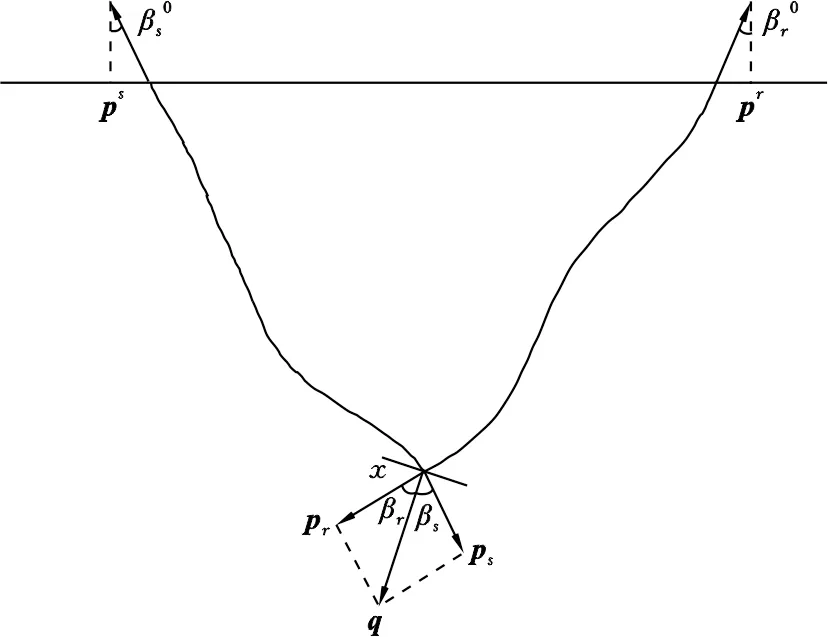
圖1 射線偏移與射線向量示意圖
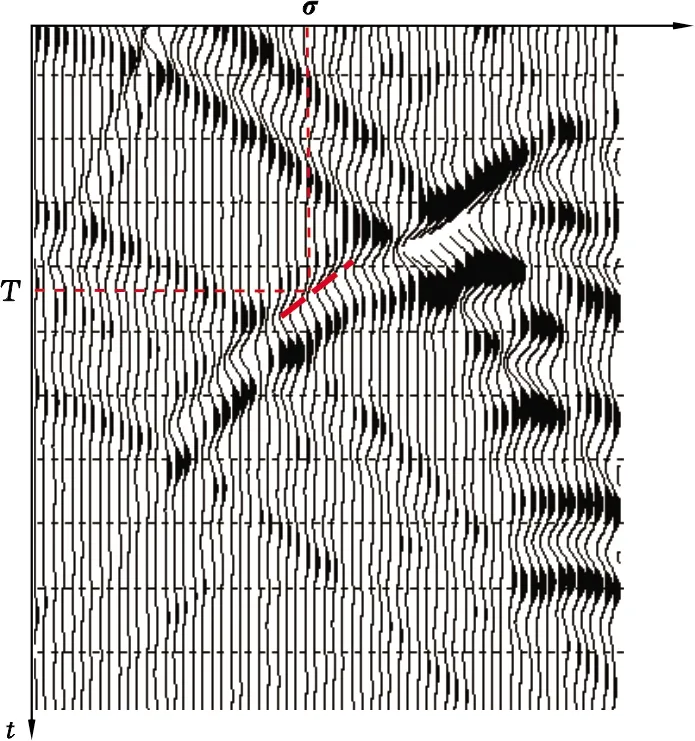
圖2 地面射線向量求取示意圖
(7)
對(duì)于覆蓋次數(shù)為r的數(shù)據(jù),Xu等[17]證明了上述成像條件的等價(jià)形式為
(8)
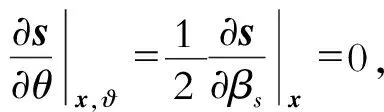
3 地下角度域波場(chǎng)分解與成像
在地震數(shù)據(jù)有效頻帶范圍內(nèi),由于所選擇的高斯束的初始寬度使走時(shí)和振幅在一個(gè)地震波長(zhǎng)范圍內(nèi)緩慢變化[9],在實(shí)際計(jì)算過(guò)程中,可以利用大網(wǎng)格計(jì)算走時(shí)和射線參數(shù),然后利用其對(duì)成像的細(xì)網(wǎng)格進(jìn)行插值得到走時(shí)和射線參數(shù),以提高計(jì)算效率。假設(shè)粗網(wǎng)格上下左右4個(gè)網(wǎng)格點(diǎn)上的走時(shí)分別為tu、td、tl、tr,網(wǎng)格縱向與橫向的步長(zhǎng)分別為Δx、Δz,網(wǎng)格點(diǎn)中心處的走時(shí)為tm(圖3),對(duì)走時(shí)進(jìn)行雙曲展開(kāi),則上、下、左、右4個(gè)點(diǎn)處的走時(shí)可以表示為網(wǎng)格中心點(diǎn)處的走時(shí)如下[16]:
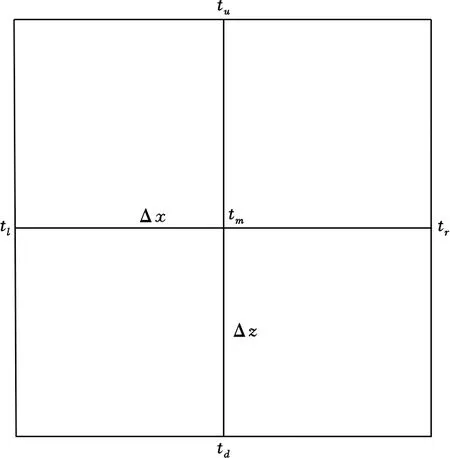
圖3 粗網(wǎng)格示意圖
(9)
式(9)中:gx為走時(shí)在水平方向一階導(dǎo)數(shù);gxx為走時(shí)在水平方向二階導(dǎo)數(shù);gz為走時(shí)在垂直方向一階導(dǎo)數(shù);gzz為走時(shí)在垂直方向二階導(dǎo)數(shù)。可以進(jìn)一步推導(dǎo)出射線參數(shù)表達(dá)式為
(10)
射線與垂直方向的夾角θ可以表示為
(11)
在求得粗網(wǎng)格點(diǎn)處射線角度以后,通過(guò)對(duì)粗網(wǎng)格點(diǎn)上的射線角度進(jìn)行插值便可以求出成像網(wǎng)格點(diǎn)上的入射射線角度θs及反射射線角度θr,進(jìn)而求出地下局部反射角θi=|θr-θs|/2,然后根據(jù)地下局部反射將成像結(jié)果求和在共成像點(diǎn)道集所對(duì)應(yīng)的角度范圍,得到地下局部共反射角度域道集,最后將地下局部共反射角度域道集所有角度進(jìn)行疊加便得到最終的成像結(jié)果。
4 數(shù)據(jù)測(cè)試
首先通過(guò)一個(gè)包含水平及傾斜界面的理論模型Ⅰ分析常規(guī)入射角道集與地下局部共反射角道集的差異,速度模型如圖4所示,采用海上拖纜采集觀測(cè)系統(tǒng),放炮方向從左到右,最大偏移距為6 000 m,最小偏移距為0 m,炮間距為25 m。圖5為克希霍夫偏移與地下局部共反射角道集偏移成像對(duì)比,可以看出,對(duì)于模型I,二者成像結(jié)果相差不大。圖6為克希霍夫偏移與地下局部共反射角道集偏移角度域道集對(duì)比,可以看到,對(duì)于水平地層,共入射角道集與地下共反射角道集基本相同,而對(duì)于傾斜地層,共入射角道集能量分布范圍與水平地層能量分布范圍一致,地下共反射角道集能量分布范圍明顯減小,地層傾角越大,其角度范圍越小。由于角度范圍存在差異,疊前AVA分析則會(huì)產(chǎn)生誤差。由于疊前AVA分析是基于共反射角的,因此,對(duì)于傾斜地層,地下局部角度域道集才能滿足AVA理論假設(shè)。
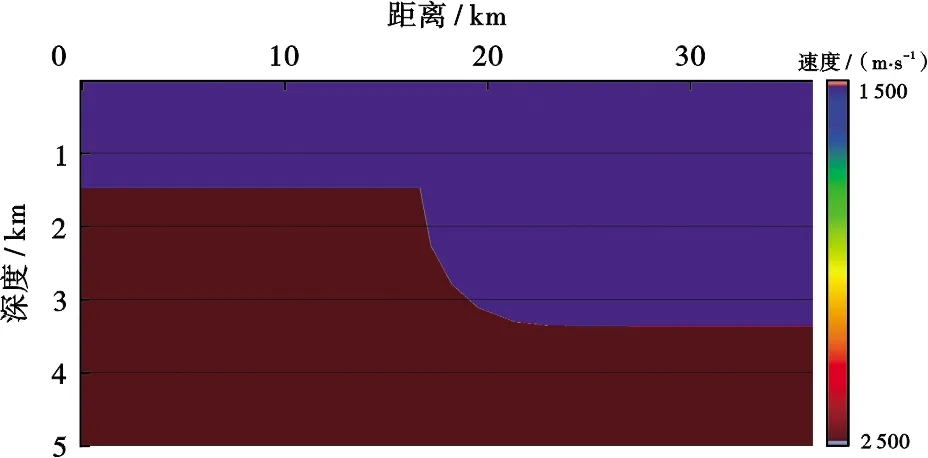
圖4 理論模型I
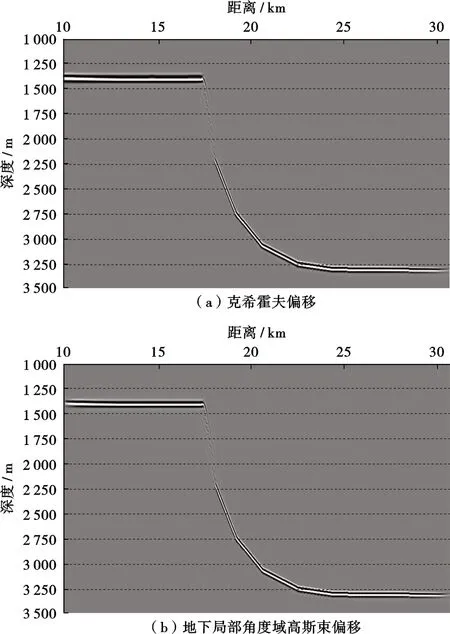
圖5 理論模型I的偏移成像對(duì)比
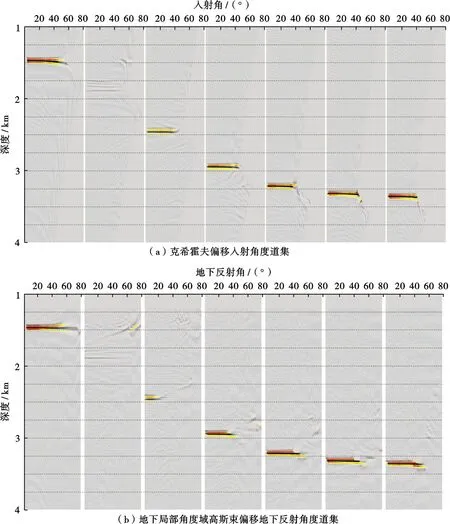
圖6 理論模型I的偏移道集對(duì)比
然后通過(guò)Marmousi復(fù)雜模型來(lái)測(cè)試本文偏移算法對(duì)復(fù)雜構(gòu)造的成像能力,所采用的采集觀測(cè)系統(tǒng)與上述理論模型一致,偏移速度為真實(shí)速度采用50 m×50 m大小窗口滑動(dòng)平均平滑后的速度(圖7)。從圖8中可以看到,克希霍夫偏移對(duì)復(fù)雜斷塊下伏構(gòu)造難以有效成像。其成像結(jié)果表現(xiàn)為高角度偏移噪音,而地下局部角度域高斯束偏移則可以對(duì)其進(jìn)行較好地成像,此外,復(fù)雜斷塊內(nèi)部(圖中橢圓形標(biāo)注區(qū)域),克希霍夫偏移也存在較多偏移畫(huà)弧噪音,尤其是復(fù)雜斷塊底部,其斷面及斷塊基本無(wú)法成像,而地下局部角度域高斯束偏移結(jié)果斷面歸位準(zhǔn)確、斷塊清晰分塊性較好。圖9為圖8中虛線處的偏移道集,其道集均為角度域道集,對(duì)于非復(fù)雜構(gòu)造區(qū)域,克希霍夫偏移道集與地下局部角度域高斯束偏移道集相差不大,對(duì)于復(fù)雜斷塊內(nèi)部及下伏區(qū)域,克希霍夫偏移角道集無(wú)連續(xù)反射同相軸,主要以高頻噪音為主,而地下局部角度域高斯束偏移道集信噪比較高、同相軸比較連續(xù),此外,受上覆復(fù)雜地層影響,其反射角均比較大,其角度道集能量主要分布在大角度范圍。與層狀模型不同的是,對(duì)于復(fù)雜構(gòu)造,其能量分布范圍并非是集中在小角度范圍,其角度分布范圍與構(gòu)造及觀測(cè)系統(tǒng)相關(guān)。因此,要想得到較為可靠的疊前AVA分析結(jié)果,傳統(tǒng)的克希霍夫偏移距道集轉(zhuǎn)換的入射角度道集可能不再滿足疊前AVA理論,須采用地下共反射角道集。
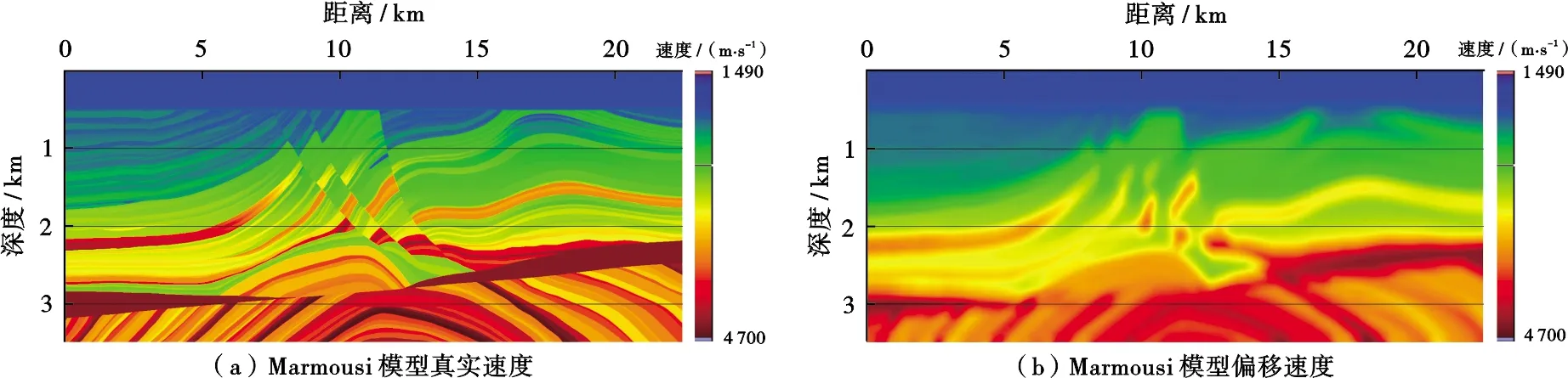
圖7 Marmousi模型速度及偏移速度
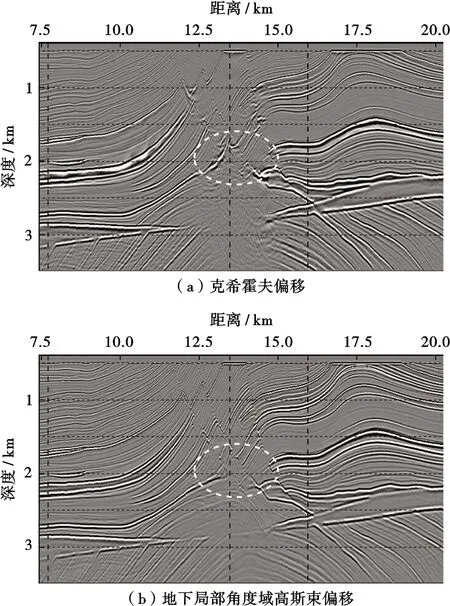
圖8 Marmousi模型偏移成像對(duì)比
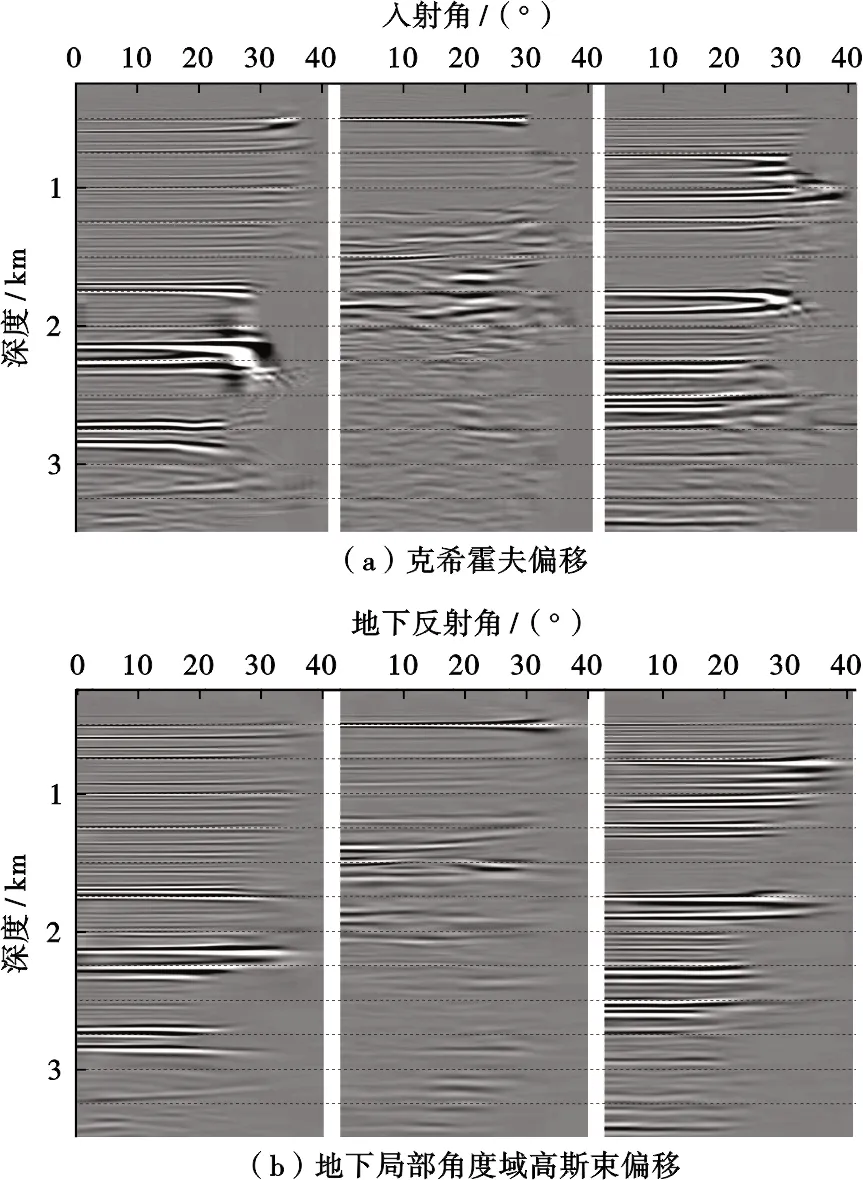
圖9 Marmousi模型偏移道集
最后對(duì)實(shí)際數(shù)據(jù)的克希霍夫與地下局部角度域高斯束偏移成像進(jìn)行對(duì)比(圖10),兩者所使用的偏移速度相同。從圖10可以看到,地下局部角度域高斯束偏移成像信噪比明顯高于克希霍夫偏移成像,淺層同相軸連續(xù)性更好;復(fù)雜斷塊內(nèi)部斷塊成像分塊性更好,該區(qū)域斷塊油氣藏地質(zhì)認(rèn)識(shí)更加清楚,有助于復(fù)雜斷塊內(nèi)部油氣勘探挖潛;斷面成像更加清楚,斷點(diǎn)更加干脆,箭頭所指處為克希霍夫偏移無(wú)法成像的小斷層,地下局部角度域高斯束偏移成像卻非常清楚。
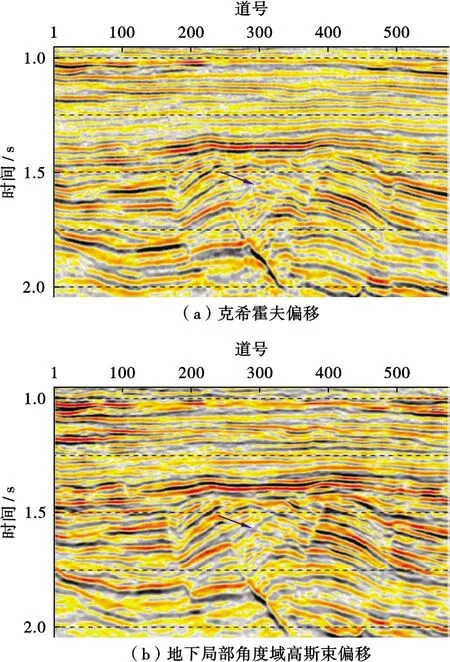
圖10 復(fù)雜斷塊實(shí)際數(shù)據(jù)偏移成像對(duì)比
5 結(jié)論
為了解決克希霍夫偏移針對(duì)復(fù)雜構(gòu)造成像能力不足及實(shí)際數(shù)據(jù)處理時(shí)效需求,本文研究了計(jì)算效率較高的地下局部角度域高斯束偏移方法。文中所述方法綜合了射線偏移高效、高斯束偏移高精度、地下角度域成像高保幅保真的特點(diǎn),具有較高的實(shí)用性。模型數(shù)據(jù)及實(shí)際數(shù)據(jù)計(jì)算表明,針對(duì)復(fù)雜構(gòu)造,本文偏移方法極大地減少了偏移假象,成像質(zhì)量明顯優(yōu)于克希霍夫偏移。此外,地下角度域道集表現(xiàn)出了高保幅保真特點(diǎn),復(fù)雜構(gòu)造道集信噪比及連續(xù)性明顯高于克希霍夫偏移入射角道集;道集反射能量分布亦不同于克希霍夫偏移入射角道集,而是與觀測(cè)系統(tǒng)及地下構(gòu)造形態(tài)相關(guān),為真實(shí)地下反射角道集,更加適合疊前AVA分析。

