Spss數據回歸分析與灰色預測
◎劉 淋 (福建船政交通職業學院,福建 福州 35007)
在信息技術騰飛的時代,數學教學內容也在發生著不少的變化.新世紀的學生已經不滿足于煩瑣、枯燥的數學公式和按部就班的計算,更多的是追求數學在生活中的實際應用,以及如何結合當下各種數學軟件進行應用.基于以上種種,現在我們的高職數學課程演變出專業性更強的各種基礎課.例如土建數學、航海數學、計算機數學基礎等等,讓不同專業的學生能結合自己的專業中的數學問題進行深入的研究和學習.在課程教學中,我們采用與現實生活相近的例子,對學生進行數學知識的實用教學,并且應用當下比較熱門的數學軟件來解決專業課程中所涉及的數學問題.
Spss,“統計產品與服務解決方案”軟件.Spss采用類似EXCEL表格的方式輸入與管理數據,數據接口較為通用,能方便地從其他數據庫中讀入數據.在我們土木建筑專業和經濟學專業中也越來越多的開始使用其來解決專業中的各種問題.專業中常常有大量的實驗數據,學生需要觀察數據.因此學生要學會對數據進行整理分析,并提取數據中的非異常點進行數據的擬合,尋找數據背后所包含的事件發展的規律.
下面以生活中實際例子為例,詳細介紹Spss在其數據擬合和預測中的應用.
福州市近年來的房價變化情況是全國各大中城市的一個縮影.表1列出了福州市近年來新建商品住宅平均銷售價格的部分數據.

表1
通過上表數據,預測下個月(即2019年4月),福州的房價.
方法一:我們對原始數據,進行擬合預測.
打開Spss軟件;在數據中輸入圖1.接著按照圖2的步驟,在跳出的窗口中,自變量輸入x,因變量輸入y,對原始數據進行冪的擬合.擬合出的函數圖像如圖3.

圖1

圖2

圖3
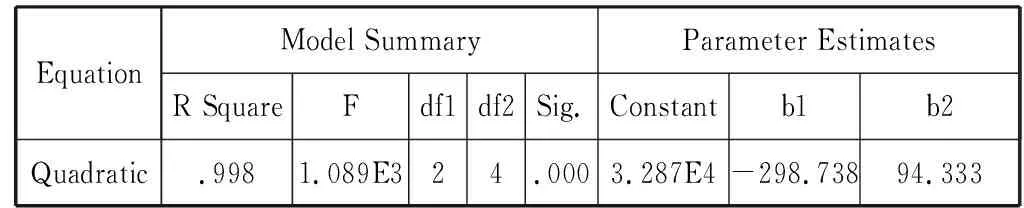
用不同級別的多項式對表格數據進行擬合后,得到比較完美的曲線方程.導出結果,得到房價增長的二次擬合方程.方程為:y=94.333x2-298.738x+32870,將x=8代入上式,得出y=36517.
EquationModel SummaryParameter EstimatesR SquareFdf1df2Sig.Constantb1b2Quadratic.9981.089E324.0003.287E4-298.73894.333
從Spss數據處理結果看R2=0.998接近1,擬合優度很高.
對于曲線的擬合,我們也可以指導學生使用Geogebra軟件的手機版本,讓每一個學生,不需要使用電腦,僅僅像打開手機微信一樣,在手機上就可以對上面例題的數據進行擬合.Geogebra軟件的結果為:y=95.4x2-309.24x+32892.43,由于各個軟件的默認函數系數小數保留的不同,對于擬合后的方程來說略有不同.將x=8代入上式,得出y=36524,與Spss軟件的差距在萬分之2左右,擬合出的曲線方程優度是很高的.
除了對所給的數據進行曲線擬合外,我們還可以用另外一種方法——灰色預測.在使用這兩種方法后,我們可以對其優劣進行比較.
方法二:我們采用灰色預測對數據進行處理.
灰色預測的主要特點是模型使用的不是原始數據序列,而是生成的數據序列.其核心體系是灰色模型(Grey Model,簡稱GM),即對原始數據做累加生成(或其他方法生成)得到近似的指數規律,再進行建模的方法.對于本題,我們采用灰色預測模型GM(1,1)模型,原因是它不需要很多的數據,一般只需要4-5個原始數據就夠,能解決數據少或序列的完整性及可靠性低的問題.同時能將無規律的原始數據進行生成,得到規律性較強的生成序列,運算簡便,易于檢驗.它的缺點是只適用于中短期的預測,只適合指數增長的預測.灰色預測是一種對含有不確定因素的系統進行預測的方法.灰色預測通過鑒別系統因素之間發展趨勢的相異程度,即進行關聯分析,對原始數據進行生成處理,來尋找系統變動的規律,生成有較強規律性的數據序列,然后建立相應的微分方程模型,從而預測事物未來的發展趨勢.
常用的生成方式有累加生成、累減生成、均值生成、級比生成等.通過觀察數據,我們采用累加生成對原始數據進行處理.對于灰色預測原始數據的選擇,由于灰色預測最好的數據是選擇前5-8個數據,故本模型選擇下面表2的原始數據對下一個月的房價進行預測.x(0)(k)表示當月的房價,x(1)(k)表示對前面月份房價進行累加生成的數據.

表2 一次累加數據


yN=(32689,32885,33148,33678,34486,35417)T,利用Geogebra的矩陣運算命令得:
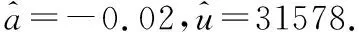
把上面的值帶入時間響應方程得:
通過上面的式子,先計算出新的累加值x(1)(k),再根據累減原理,還原x(0)(k).
同樣得出2019年4月的月均房價為36705元.

