二階脈沖隨機微分方程積分邊值問題解的存在性
孫會賢,顧海波,馬麗娜
(新疆師范大學 數學科學學院,新疆 烏魯木齊 830017)
0 引言
積分微分方程通常被用來刻畫生物模型、化學動力學、流體力學等現實生活中的很多現象。實際上,用隨機微分方程或者隨機積分微分方程來描述一些自然現象更為合理[1-5]。另外,在很多動力系統中都會有脈沖現象的存在,所以在考慮隨機干擾的同時考慮到脈沖的影響很有必要,脈沖微分方程的特點引起了學者們的關注。近年來,許多學者研究了固定脈沖微分方程的初邊值問題[6-9]。2019年,文獻[10]研究了二階非線性積分邊值問題
正解的存在唯一性,且存在t0∈[η,1]使得a(t0)>0。
Zhao和Chen[11]研究了二階脈沖微分方程邊值問題
a>0,b≥0,c>0,d≥0,0=t0 解的存在唯一性。 2011年,Xia和Lin[12]討論了隨機微分方程兩點邊值問題 其中T>0,A和B為d×d階矩陣,{W(t),0≤t≤T}是k維標準布朗運動,給出了自適應解存在的充要條件,并對于特殊選擇的解,得到了邊值問題的連續相依性。 2020年,Dong[3]研究了隨機分數階積分微分方程 受此啟發,本文將以往所研究的方程的脈沖項和邊界條件做了推廣,對其限制條件進行了修改,考慮帶有脈沖的二階隨機微分方程的積分邊值問題 (1) 其中f:J×R×R→R連續,w=(w1,w2,…,wn)T是給定的n維標準布朗運動, 假定(Ω,Γ,P)是一個完備的概率空間,其中Ω是一個樣本空間(或任意一個集合),Γ是由Ω的部分子集構成的集合族,Γ中的元素稱為事件,P是(Ω,Γ)上的概率,Lq(Ω,Rn)為強可測空間,滿足q次可積,且u:Ω→Rn為任意Γt可測d維隨機變量。 則PC(J,L2(Ω,Rn))構成一個Banach空間。 則PC1(J,L2(Ω,Rn))構成一個Banach空間。 引理1[13]基本不等式 (ⅰ)p>0,|a+b+c|p≤3p-1(|a|p+|b|p+|c|p); (ⅲ) Doob鞅不等式 定義1 如果u(t)滿足: (ⅰ)u(t)是Γt適應的且在(tk,tk+1)處是連續的; (ⅳ) 對于任意給定T∈J,u(t)在t∈[0,T]{tk}上幾乎處處滿足方程(1),則稱u(t)是方程(1)在[0,T]上的解。 引理2(Ascoli-Arzela定理)[14]設S={s(t)}是一個由連續映射s:[a,b]→PC1構成的函數族。若對于任意的t*∈[a,b],集合s(t*)是相對緊的,則S是一致有界且等度連續的,并在S中存在一致收斂函數序列{sn(t)},n=1,2,…,t∈[a,b]。 引理3(Leray-Schauder定理)[14]設PC1為實Banach空間,算子A:PC1→PC1為全連續算子,若集合u∈{u∈PC1|u=λAu,0<λ<1}是有界的,則u=Au至少有一個解。 引理4 設ση2≠2,則邊值問題(1)的解u∈PC1(J,L2(Ω,Rn))∩PC2(J′,L2(Ω,Rn))等價于脈沖積分方程 (2) 的解,其中 證明設u是邊值問題(1)的解,對式(1)兩端積分得 (3) 對式(3)再次積分得 (4) 對式(4)兩端進行積分 并對式(4)取t=1,得 結合邊值條件可得 將上式代入(4)式得 證畢。 引理5[15]格林函數G(t,s)具有以下性質: (1)G(t,s)在[0,1]×[0,1]上連續; 本節通過運用Leray-Schauder定理討論了邊值問題(1)解的存在性。為了方便,下面將給出所需假設條件及記號說明。本文中,對任意x,y∈R假設如下: (H1)函數f(t,x,y)在J×R×R上連續,函數g(t,x)在J×R上連續。 (H2)存在正常數L,使得|g(t,x)|≤L(1+|x|2)。 (H3)存在有界函數α(t),β(t),γ(t)使得|f(t,x,y)|≤α(t)|x|+β(t)|y|+γ(t)。 (H4)存在非負常數ak,bk,ck,k=1,2,3,…,n,使得 (H5)存在非負常數nk>0,k=1,2,…,n,使得 記 首先定義算子A:PC1→PC1如下 (5) 并對式(5)關于t求導,即 定理1 若假設條件(H1)~(H5)成立,且滿足1-F1>0,則邊值問題(1)至少存在一個解。 證明定理的證明可分解為以下4個步驟: (1)先證A是一個連續算子,對于任意{un}∈PC1,存在u0∈PC1,使得un→u0(n→∞)。 并且有 當n→∞時,根據f,g,G的連續性可知,E‖(Aun)(t)-(Au0)(t)‖2→0且 E‖(Au′n)(t)-(Au′0)(t)‖2→0。 因此,A在PC1上是一個連續算子。 (2)對任意的u∈PC1,且u(0)=0,則由 可得 則 因此,只需驗證E‖(Au′)(t)‖2一致有界即可。并且由(H5)可得,存在Nk>0,k=1,2,…,n,有 從而 其中 因此,結合(H3)可得 (6) (3)對任意的u∈PC1,v1,v2∈(tk,tk+1),當t1 (7) 由(7)式可知,當|t1-t2|→0時,E‖(Au)(t1)-(Au)(t2)‖2→0,對任意的有界集Ω∈PC1,結合(6)(7)式可知,A(Ω),A′(Ω)在每個Jk上等度連續,因此推出A是等度連續的,即A在PC1上是相對緊的。運用引理2(Ascoli-Arzela定理)可知A:PC1→PC1是全連續算子。 (4)對任意u∈{u∈PC1|u=λAu,0<λ<1},對u(t)=λAu(t),其中λ∈(0,1)有 從而有‖u‖=sup|λ(Au)(t)|≤‖(Au)(t)‖≤C,得到u∈{u∈PC1|u=λAu,0<λ<1}是有界的,由引理2、引理3可知,方程(1)的解等價于算子A的不動點,即邊值問題(1)至少有一個解,證畢。 考察二階脈沖隨機微分方程 (8) 其中 易知 從而邊值問題(8)滿足定理1的所有條件,因此邊值問題(8)至少存在一個解。
1 預備知識






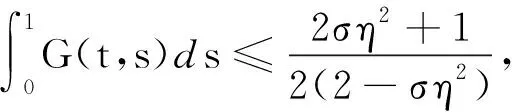
2 主要結果

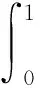


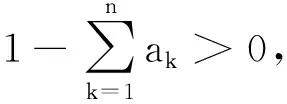

3 應用舉例

