基于代價參考粒子濾波器組的檢測前跟蹤算法

盧 錦 王 鑫

(陜西科技大學電子信息與人工智能學院 西安 710021)

1 引言

延長觀測時間是雷達中檢測微弱目標的有效方法。但在較長的觀測時間內，目標機動性等給信號積累帶來困難。例如，在天波雷達中，在較長的觀測時間內，目標處在同一個檢測單元內，但轉向或加速等使目標回波具有復雜的調頻特性，可模擬為未知的非線性調頻信號[1–4]。此種情況下，長時間信號積累檢測微弱目標的問題，即是檢測低信噪比的非線性調頻信號的問題。

國內外學者提出了很多檢測非線性調頻信號的方法，從檢測結果看，可將這些方法分為兩類。第1類，基于非線性調頻信號的狀態估計結果累積觀測數據，通過門限比較實現給定虛警率下的檢測。文獻[5]中的脊能量檢測方法和文獻[6]中的時頻分布累積方法，都是沿瞬時頻率曲線在頻域累積觀測數據能量實現目標檢測。此外，文獻[7]基于粒子濾波(Particle Filter,PF)構造觀測數據的聯合似然比，文獻[8,9]基于代價參考粒子濾波(Cost-Reference Particle Filter,CRPF)和FB-CRPF(Forward-Backward CRPF)構造累積代價，也是通過累積觀測數據的能量實現目標檢測。第2類方法主要是基于PF的檢測前跟蹤(Track-Before-Detecting,TBD)方法(PF-TBD)[10,11]。此類方法在目標狀態向量中增加表示目標存在狀態的離散變量，估計各個時刻的目標存在概率，當存在概率大于給定門限時，即判斷目標在該時刻存在。

上述兩類方法中，第1類方法雖然可提供給定虛警概率下的目標檢測，但無法判斷目標出現和消失的具體時刻；第2類方法雖然能夠判斷目標出現和消失的具體時刻，但采用存在概率描述檢測能力，較難用常規的檢測概率和虛警概率衡量算法性能。

上述兩類方法的關鍵都是非線性調頻信號的瞬時頻率估計，瞬時頻率估計精度與檢測能力直接相關。PF類方法用大量帶有權值的隨機樣本近似目標狀態的后驗概率密度函數，可提供更準確的非線性調頻信號瞬時頻率估計，廣泛應用于雷達信號處理、圖像處理等領域[12–16]。但PF類方法的狀態估計精度與收斂速度直接相關。通常，非線性調頻信號檢測問題的先驗信息非常有限，導致PF類方法的收斂速度較慢。此外，有限的先驗信息要獲得較好的估計結果，就需要大量樣本，大量的樣本必然帶來巨大的計算量。而PF類算法的并行化執行一直是一個難題。因而，在先驗信息非常有限的情況下，收斂速度和計算復雜度是限制PF類檢測方法的主要因素。

針對PF類算法收斂慢和計算復雜度高的問題，本文提出一種具有完全并行結構的CRPF[17,18]，即CRPF濾波器組(CRPF bank)。基于CRPF濾波器組的估計結果，分別累積各段觀測信號，將各段的累積能量與給定門限比較，實現給定虛警概率下目標在各個時刻的目標檢測。仿真結果表明，與現有的PF-TBD方法相比，本文提出的方法檢測能力強，運行速率高。

2 代價參考粒子濾波器組

2.1 狀態空間模型

以天波雷達為例，假設在觀測時間t∈[0,Tob]s內，目標處于一個檢測單元中。此時目標檢測問題可歸結為如式(1)的二元假設檢驗問題

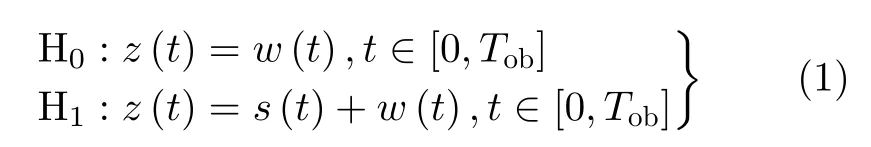
若 H0成立，則目標不存在，觀測z(t)僅包含未知的背景噪聲w(t)；若H1成立，則目標存在，觀測z(t)是 未知的非線性調頻信號s(t)與未知的背景噪聲w(t)的混合，如式(1)所示。目標檢測問題就是根據觀測z(t)來 判斷H0成立或H1成立。

若采用基于PF的方法處理上述二元假設檢驗問題，則要先假設 H1成立，在此基礎上建立狀態空間模型來估計目標狀態。本文提出的CRPF濾波器組也是一類PF算法，因此需要建立狀態空間模型。下面，假設 H1成 立，將回波信號s(t)近似為分段線性調頻信號來建立狀態空間模型，以估計s(t)的瞬時頻率。

基于式(9)和式(10)的狀態空間模型，非線性調頻信號的瞬時頻率曲線估計問題轉化為從觀測序列ZK={z1,z2,...,zK}中估計狀態序列X={x1,x2,...,xK}。基于狀態估計結果和觀測序列，可進行目標檢測。

2.2 CRPF濾波器組的結構

基于2.1節的分段調頻信號狀態空間模型，本節提出CRPF濾波器組來快速、準確地估計非線性調頻信號的瞬時頻率。圖1是CRPF濾波器組的基本結構，包括M個并行的CRPF，每個CRPF采用相同的狀態空間模型，如式(9)、式(10)所示，但先驗信息不同。

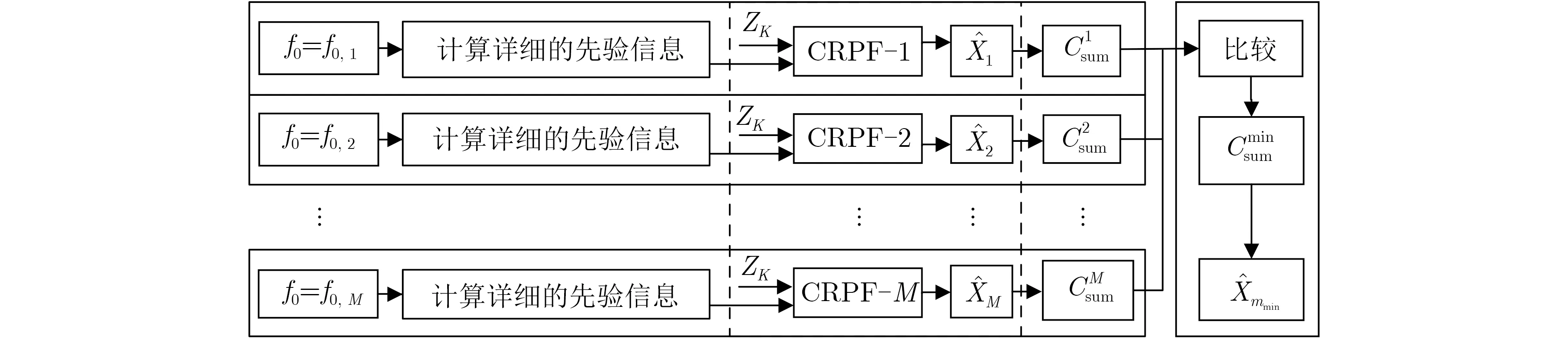
圖1 CRPF濾波器組的結構

(4)比較M個CRPF的累積代價，將累積代價最小的CRPF的估計結果作為CRPF濾波器組的估計結果。

顯然，步驟(1)—步驟(3)可并行執行。因此，CRPF濾波器組的運行時間Ttotal為

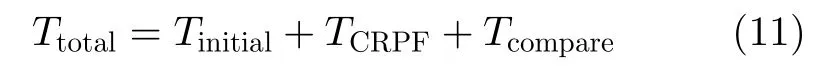
式中，Tinitial表示計算第m個CRPF的更精確的先驗信息的計算時間，TCRPF表示第m個CRPF的運行時間，Tcompare表示比較M個累積代價的時間。

2.3 計算詳細的先驗信息

那么如何為第m個CRPF設計更精確的先驗信息呢？本節詳述此問題。

從式(8)的系統方程可得關系

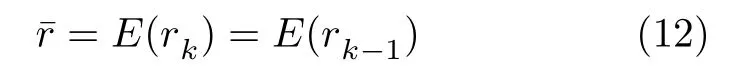
此外，由式(8)可從多普勒頻率估計調頻率

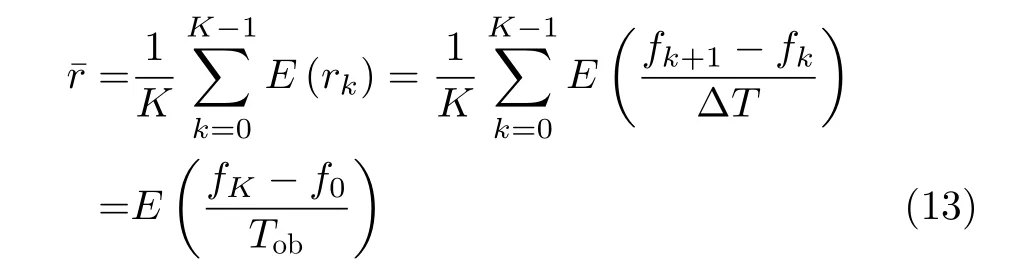
結合先驗信息f(t)∈[fmin,fmax]，由式(13)可得調頻率的均值的可能范圍為

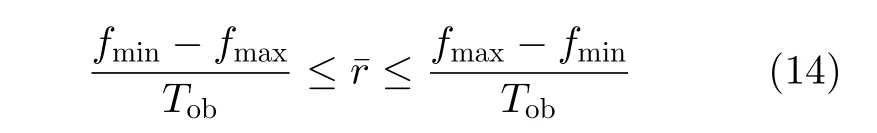
將式(14)中調頻率均值的可能范圍，近似為調頻率的可能范圍，則與先驗信息r(t)∈[rmin,rmax]相比，有以下3種情況：

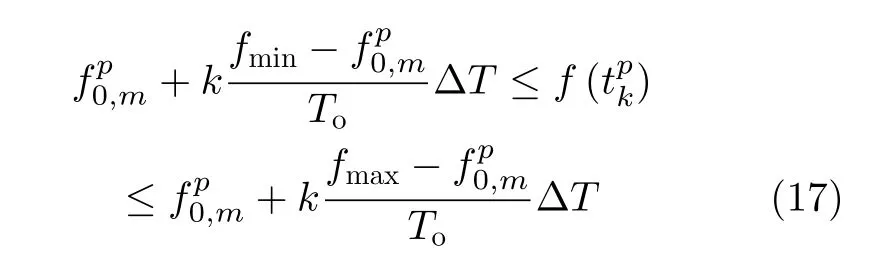
圖2比較了3種不同情況下假設的先驗信息與原有的先驗信息f(t)∈[fmin,fmax]Hz的比較，陰影部分是基于情況(1)至情況(3)獲得假設的先驗信息。可見，在分段線性調頻信號及具體的初始時刻頻率的假設下，假設的先驗信息更詳細。

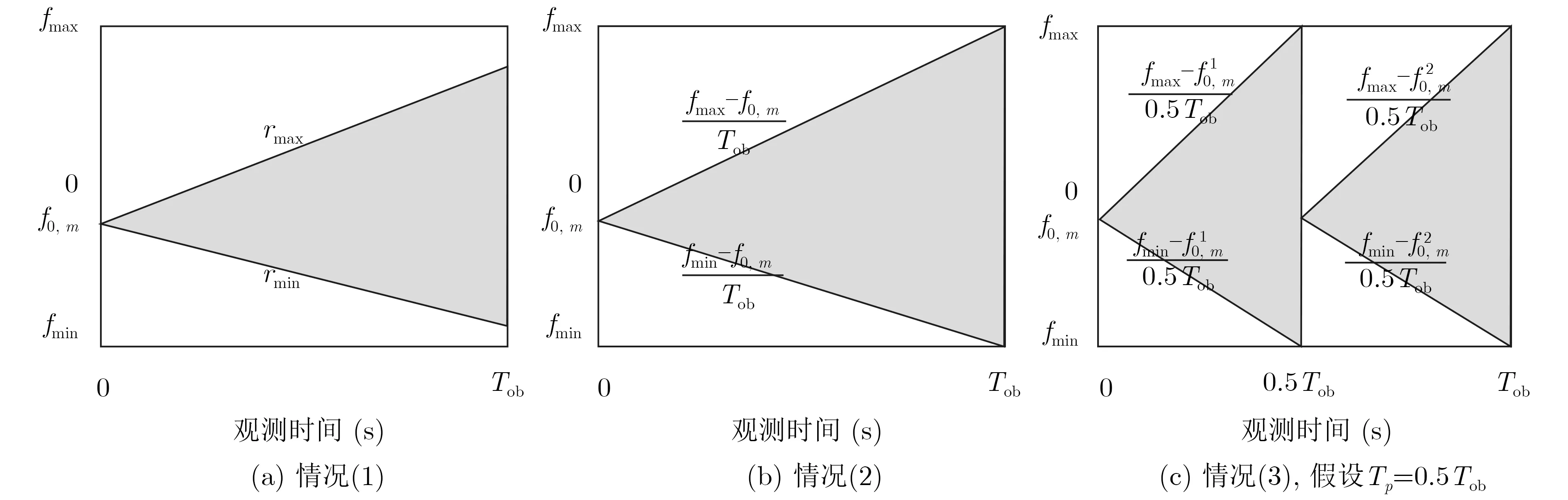
圖2 假設的先驗信息與原始先驗信息的對比

2.4 CRPF濾波器組偽碼

本節給出CRPF bank中第m個CRPF的偽碼，對應2.3節的情況(1)、情況(2)，以及情況(3)的第p段子觀測區間。

3 基于CRPF濾波器組的TBD算法

針對式(1)描述的檢測問題，本節提出一種基于CRPF濾波器組的目標檢測策略，可在給定虛警概率下，判斷目標在各個時刻是否出現，如圖3所示。

由圖3可見，基于CRPF濾波器組的檢測策略包含以下3個步驟：

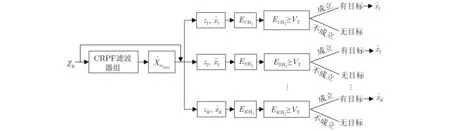
圖3 CRPF濾波器組-TBD的檢測策略

4 仿真

4.1 測試信號

為了證明CRPF濾波器組在運行速度、信號檢測性能方面的優越性，本文采用兩類測試信號

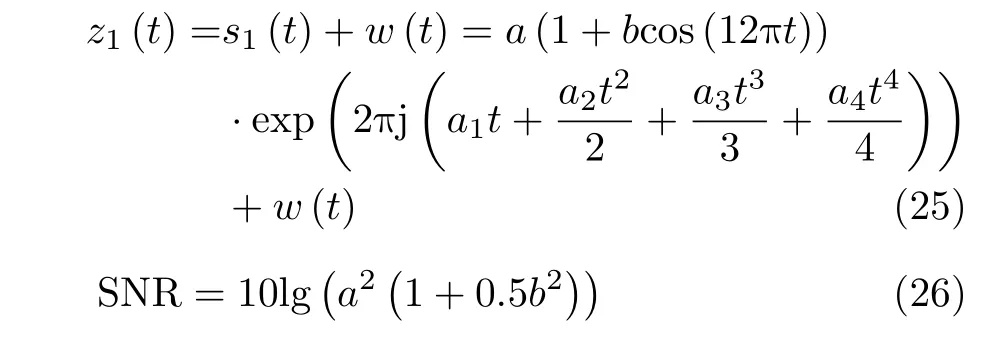
式(25)中，a(1+bcos(12πt))表示時變的信號幅度，b∈[0,1),a1,a2,a3,a4∈[-20,20] 。w(t)服從方差為1，形狀參數為0.5的復廣義高斯分布[19]。觀測信號的信噪比(Signal to Noise Ratio,SNR)如式(26)所示。

式(27)中，b∈[-40,40]，觀測信號的信噪比如式(28)所示。

4.2 CRPF濾波器組-TBD的檢測性能和瞬時頻率估計性能

圖4和圖5所示分為SNR=–9 dB,–7 dB,Pfa=0.001時，對3種測試信號，CRPF濾波器組-TBD,PF-TBD[10]和Rutten PF-TBD[11]在各個時刻的檢測概率Pd和瞬時頻率曲線的均方根誤差RMSE(Root Mean Square Error)。其中瞬時頻率曲線的RMSE定義如式(29)所示。式(29)中，f表示測試信號的瞬時頻率，表示瞬時頻率的估計，Ls=Tob/ts表示觀測序列的長度。仿真中，CRPF-濾波器組-TBD包含2000個CRPF，每個CRPF僅用1個樣本，PF-TBD和Rutten PF-TBD的樣本數是6000。PF-TBD和Rutten PF-TBD在各個時刻的檢測概率計算如下：將各個時刻的存在概率當作檢測統計量，根據虛警概率確定檢測門限，當存在概率大于檢測門限宣布目標存在，否則宣布目標不存在。此時，3種方法的檢測結果可直接比較，同樣的虛警概率下，檢測概率大者，檢測能力更強。

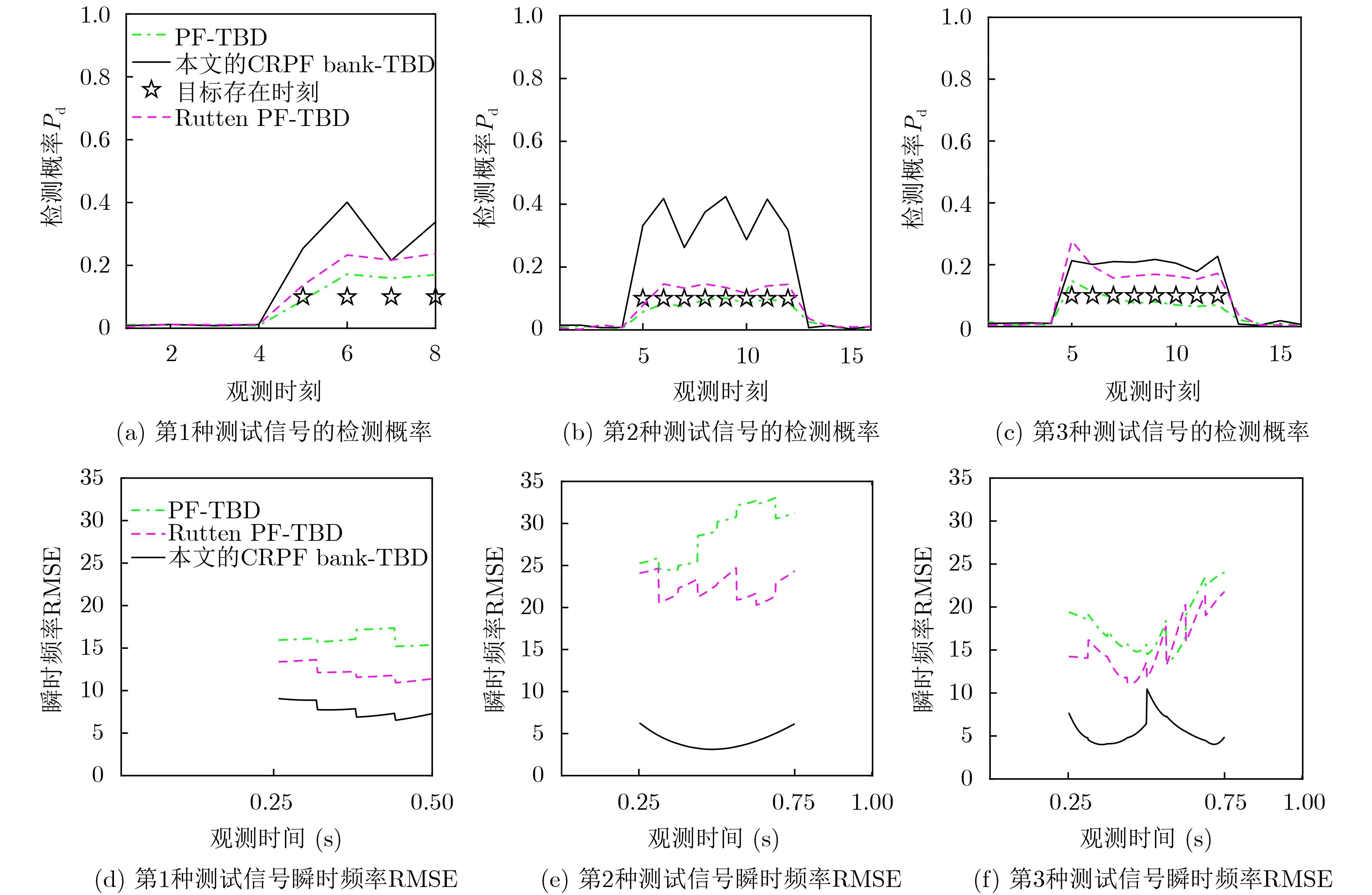
圖4 3種測試信號的檢測概率及瞬時頻率RMSE比較

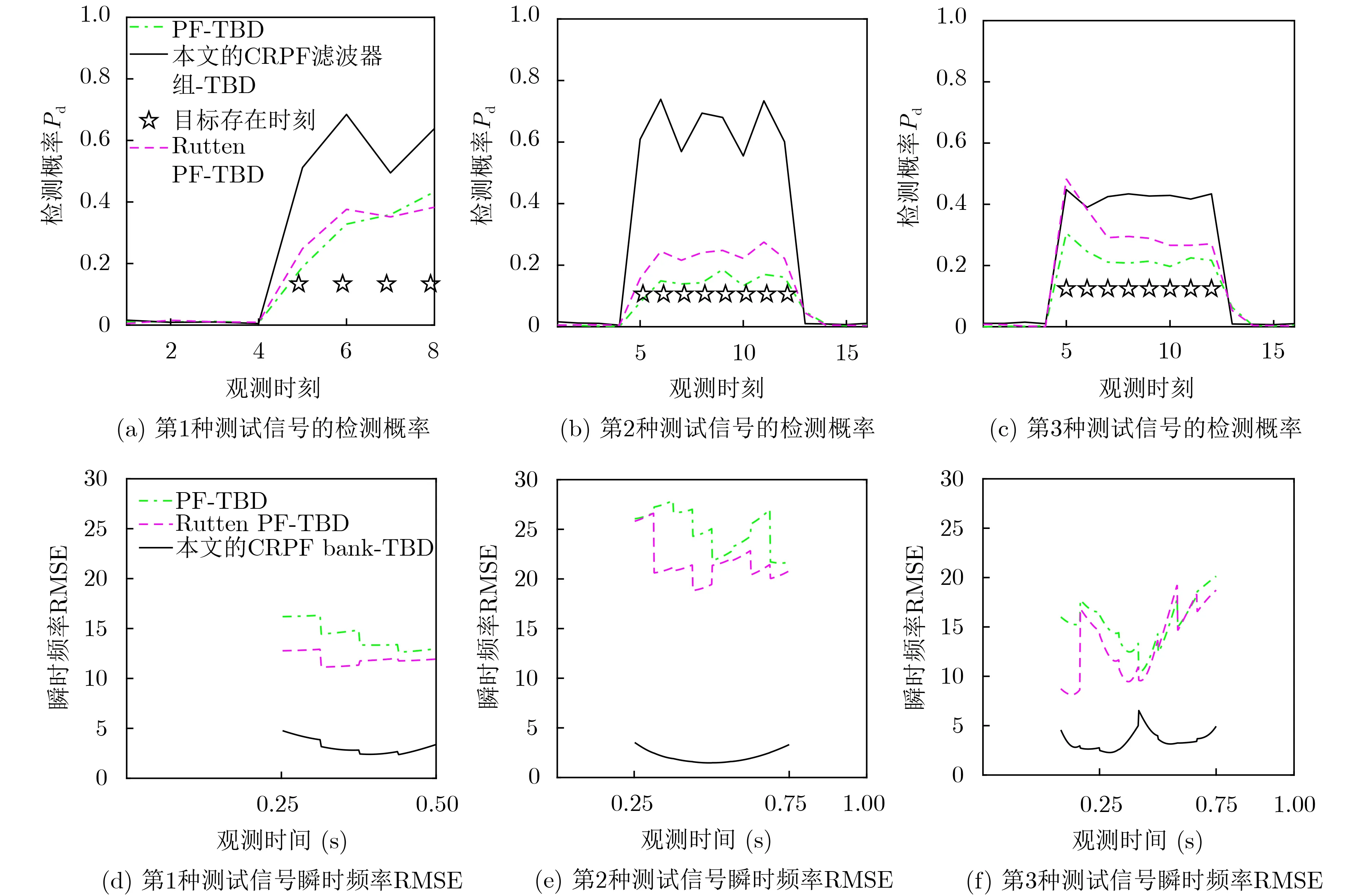
圖5 3種測試信號的檢測概率及瞬時頻率RMSE比較

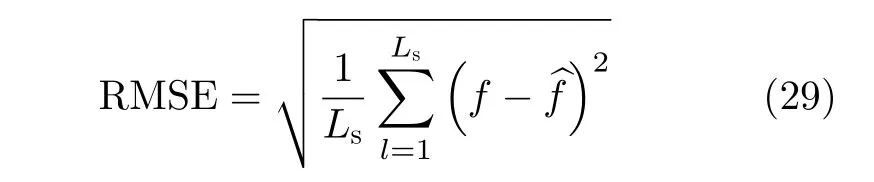
表1是PF-TBD,Rutten PF-TBD和CRPF濾波器組-TBD的平均單次運行時間。PF-TBD和Rutten PF-TBD的單次運行時間是指其處理一個觀測信號得出檢測結果的時間。CRPF濾波器組-TBD的單次運行時間是其中一個CRPF的運行時間、多個CRPF的累積代價的比較時間、各段信號積累的時間以及門限比較的時間之和，運行時間單位為s。表1表明，CRPF濾波器組-TBD的運行時間僅為PF-TBD的千分之一。

表1 本文的CRPF濾波器組-TBD與PF-TBD,Rutten PF-TBD的運行時間(s)比較

本節的仿真結果表明，本文提出的CRPF濾波器組-TBD方法的檢測和估計能力均優于同類方法，且復雜度更低，運算時間更短。

4.3 目標出現時刻及持續時間對CRPF濾波器組-TBD性能的影響

本節分析目標出現時刻及持續時間對CRPF濾波器組-TBD,PF-TBD及Rutten PF-TBD性能的影響。圖6所示是第2種測試信號，SNR=–7 dB,b=0.1，目標出現在t∈[0.25,0.75]s時，PF-TBD，Rutten PF及CRPF濾波器組-TBD在各個時刻的檢測概率和瞬時頻率曲線RMSE，以及目標出現在t∈[0.125,0.4375]s時，PF-TBD,Rutten PF及CRPF濾波器組-TBD在各個時刻的檢測概率和瞬時頻率曲線RMSE。仿真結果表明，3種方法的檢測能力和瞬時頻率估計能力對目標出現的時刻及持續的時間都不敏感。但CRPF濾波器組-TBD的檢測能力狀態瞬時頻率曲線估計精度均遠高于PFTBD及Rutten PF-TBD方法。

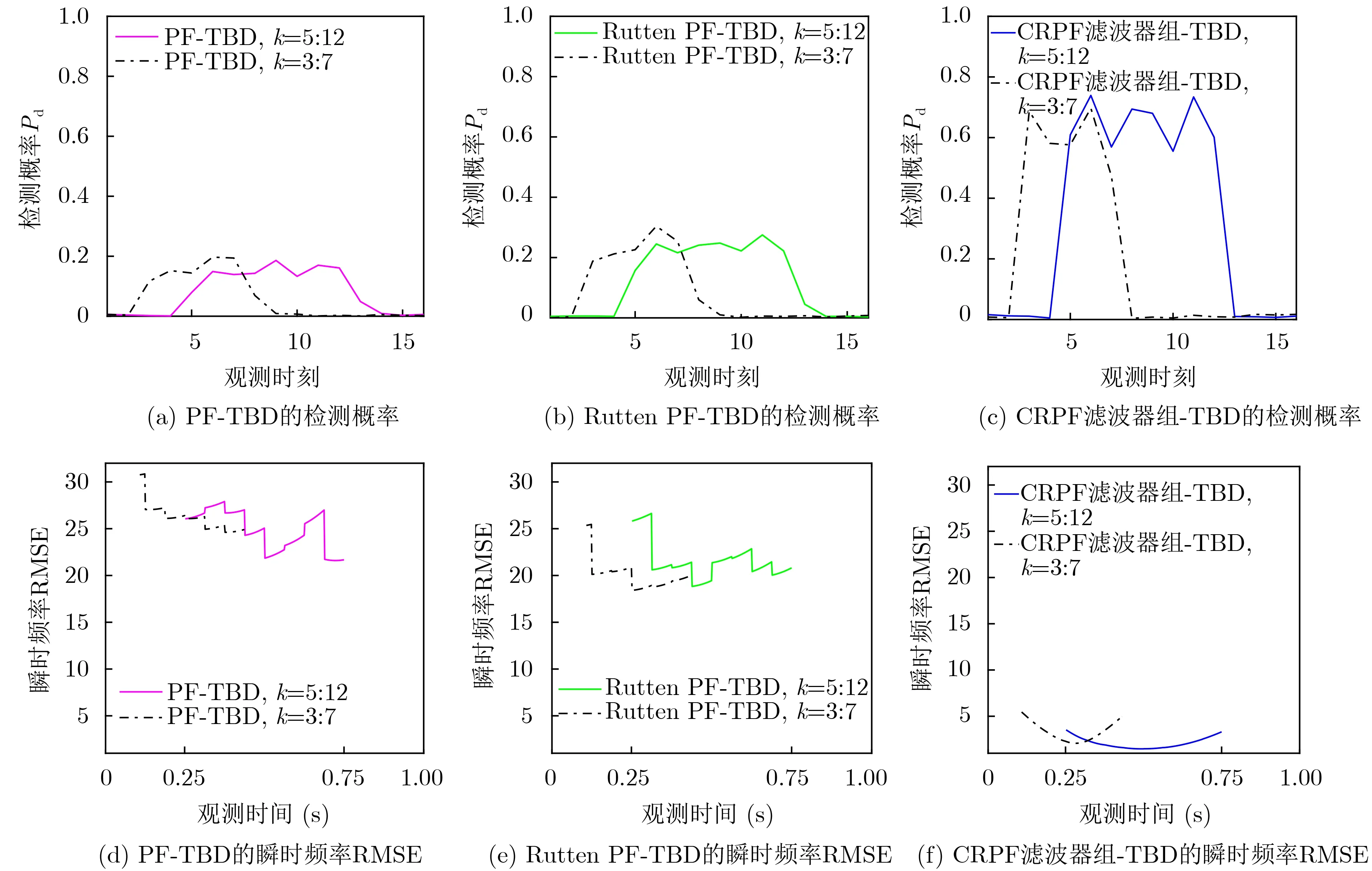
圖6 目標出現時刻及持續時間對3種方法的檢測概率及瞬時頻率RMSE的影響

4.4 CRPF 的數量、樣本數及子區間長度對CRPF濾波器組-TBD性能的影響

本節分析CRPF的數量、樣本數量及子區間長度對CRPF濾波器組-TBD性能的影響。圖7所示是第2種測試信號，SNR=–7 dB,b=0.1，目標出現在t∈[0.25,0.75]s，每個CRPF 只用1 個樣本，CRPF濾波器組-TBD包含的CRPF的數量分別為50,100,500,1000,2000,2500,3000時，CRPF濾波器組-TBD的檢測概率和瞬時頻率曲線RMSE比較。仿真結果表明，隨著CRPF的數量增加，CRPF濾波器組-TBD的檢測能力和估計能力會緩慢增加。當CRPF的數量大于2000后，CRPF濾波器組k-TBD的檢測和估計能力基本穩定。

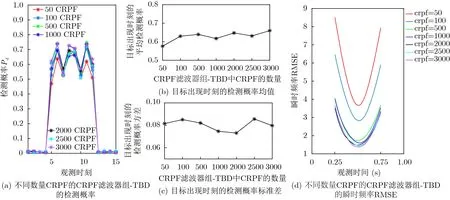
圖7 CRPF的數量對CRPF濾波器組-TBD檢測性能和估計性能的影響

圖8所示是第2種測試信號，SNR=–7 dB,b=0.1，目標出現在t∈[0.25,0.75]s，CRPF濾波器組-TBD包含2000個CRPF，各個CRPF采用的樣本數分別是N=1,5,10,20,50,100時，CRPF濾波器組-TBD的檢測概率和瞬時頻率曲線RMSE比較。仿真結果表明，隨著樣本數的數量增加，CRPF濾波器組-TBD的檢測和估計能力會下降。即在其他條件一樣的情況下，樣本數為1時CRPF濾波器組-TBD的檢測能力和瞬時頻率估計能力最好。

圖8 樣本數對CRPF濾波器組-TBD檢測性能和估計性能的影響

5 結束語

本文提出了一種具有并行結構的非線性調頻信號瞬時頻率估計方法CRPF濾波器組，并在此基礎上提出了可同時在各個時刻檢測目標和估計目標狀態的檢測前跟蹤算法CRPF濾波器組-TBD。CRPF濾波器組-TBD基于CRPF濾波器組的狀態估計結果，計算每個觀測子區間內觀測信號的增量代價，將增量代價作為各個時刻目標檢測的檢測統計量。當某一時刻的增量代價大于給定門限時，即認為該時刻目標出現。與常規的基于粒子濾波TBD方法相比，CRPF濾波器組-TBD方法可提供各個時刻的恒虛警檢測。仿真結果表明，CRPF濾波器組-TBD方法的檢測性能、估計性能及運行速度均優于同類方法。