開架式水下機器人水動力系數計算與動力學建模

閆銀坡， 于福杰， 陳原

(山東大學(威海) 機電與信息工程學院， 山東 威海 264209)

0 引言

近年來，隨著海洋勘探和開發的進展加快，水下機器人在極端作業環境下得到了廣泛應用[1]。為了實現對水下機器人運動的精確控制，水下機器人動力學模型中的水動力系數必須具有相當的準確性[2]。目前，求解水動力系數的方法主要有經驗公式估計法、船模試驗法和計算流體力學(CFD)數值模擬法[3]。其中，采用CFD技術模擬船模試驗的方法具有不受試驗設備精度影響和成本低的優點，并可提供不受外界環境干擾的理想仿真環境，因此廣泛應用于水下航行器水動力系數的計算[4-6]。

現有CFD數值模擬法多采用基于雷諾平均Navier-Stokes方程(RANS)方法的CFD軟件(Fluent，Star CCM+和CFX等商用軟件，以及基于開源平臺OpenFOAM的自主開發軟件)模擬船模試驗的方式進行。船模試驗模擬可分為穩態船模試驗模擬和非穩態船模試驗模擬。穩態船模試驗時航行器固定不動，通過系列地改變來流速度和航行器相對來流偏角(即漂角)實現對穩態縱蕩和斜航運動模擬，進而擬合求解相應的線性黏性水動力系數和耦合黏性水動力系數，相關研究見文獻[7-9]。此外，通過將求解域設置成弧形流域模擬旋轉臂試驗，可求得與搖艏角速度相關的耦合水阻尼系數[10]。但穩態運動模擬僅可用來求黏性水動力和耦合水動力系數，無法求慣性水動力系數，且需要進行多組模擬，十分耗時。通過CFD技術模擬非穩態平面運動機構(PMM)試驗，可以計算各種慣性水動力系數和黏性水動力系數，與穩態船模試驗模擬相比，非穩態PMM模擬試驗大幅度縮減了計算量。現有基于傳統CFD技術的非穩態模擬研究，多采用動網格技術、滑移網格技術和重疊網格技術等處理求解域網格的變形和重構問題[11-14]，相對于穩態運動模擬，需要更加細致的網格劃分、更長的計算時間和更高性能的計算平臺。

此外，基于RANS方法的傳統CFD技術對于具有復雜外形的水下機器人會面臨網格劃分繁瑣和計算收斂性的限制，因此研究對象多為外形簡單的水下機器人和具有完備數據參考的Suboff潛艇。另外，由于收斂性的限制，基于RANS方法和動網格技術模擬無法對大振幅PMM(LAPMM)試驗進行模擬[15]。通過模擬小振幅PMM試驗雖然可以求得慣性水動力系數和線性黏性水動力系數，但是非線性黏性水動力系數的計算需要額外的穩態運動模擬。水下機器人在進行大機動操作時，若僅考慮線性水動力系數而忽略非線性水動力系數，水下機器人所受水動力的計算值與實際值相比不僅數量上存在較大差異，且性質不同，從而導致無法實現對水下機器人的精確控制[16]。

為了建立更加符合水下機器人結構性特點的動力學模型，本文提出基于格子玻爾茲曼方法(LBM)數值模擬LAPMM試驗的水動力系數計算方法，以快速計算出這類大振幅機動操作且外形復雜的水下機器人慣性水動力系數和包含非線性項的黏性水動力系數。不同于傳統CFD數值模擬方法，基于LBM的數值模擬不再以Navier-Stokes方程為控制方程，不再基于連續介質假設，而是通過對離散流體微觀粒子的大量統計來獲得宏觀流體的運動規律[17]。LBM方法無需進行繁瑣的網格劃分，對于復雜結構的表面只需要加密網格即可；在進行大振幅非穩態運動模擬時避免了現有研究中動網格難以更新的問題，克服了對水下機器人復雜程度和非穩態運動振幅大小的限制，對水下機器人水動力系數的數值計算和動力學建模具有普適的應用意義。

1 水下機器人動力學建模

1.1 水下機器人描述與坐標系構建

本文研究對象為一款具有薄片、彎管等特殊部件的開架式遙操作水下清理機器人(ROV)，樣機及三維模型如圖1所示，其主體尺寸為長L=1.23 m，寬W=1.31 m，高H=0.60 m，質量為56.914 kg，排水量為0.067 4 m3，浮力略大于重力。ROV載體共配置6個推進器，單個推進器功率為850 W，可提供正向推力約150 N、反向推力約60 N.

圖1 ROV樣機與三維模型Fig.1 ROV prototype and 3D model

為了描述水下機器人的空間三維運動，建立運動坐標系Oxyz和慣性坐標系Eξηζ，如圖2所示。圖2坐標系中各符號和水下機器人運動參數的含義如表1所示。

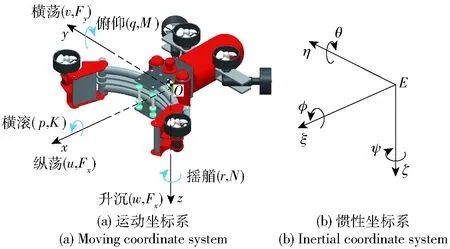
圖2 ROV坐標系的定義Fig.2 Definition of ROV coordinate system

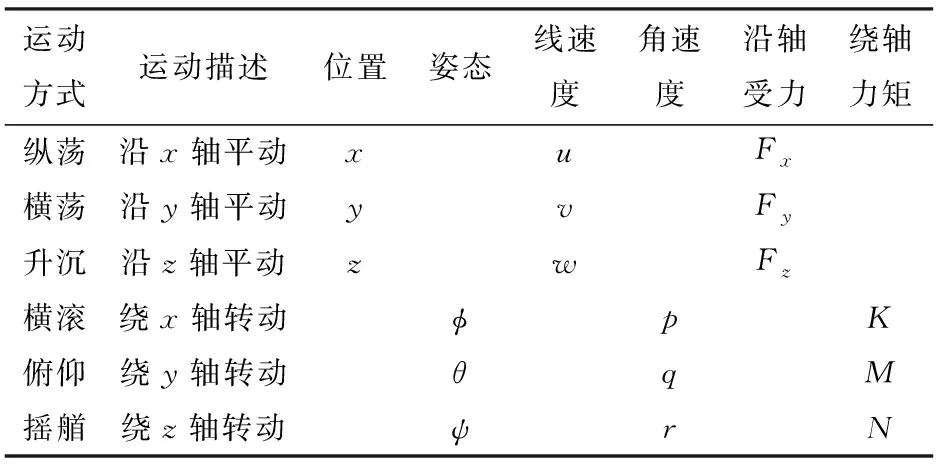
表1 ROV運動參數定義

1.2 水下機器人的動力學建模

基于1.1節的坐標系系統，定義ROV在慣性坐標系下的位姿向量η=[η1η2]T，其中η1=[xyz]T，η2=[φθψ]T；定義ROV在運動坐標系下的速度向量v=[v1v2]T，其中v1=[uvw]T，v2=[pqr]T，則ROV的運動學方程可以表示如下：

(1)

式中：

(2)

(3)

該水下機器人在y軸上具有較高的俯仰穩定性和較大的轉動慣量，因此假設俯仰角θ在[-π/2 rad -π/2 rad]內，即轉換矩陣J2不會出現奇異性問題。

ROV是一種具有強非線性耦合、強參數不確定性和未知外干擾的復雜系統，完整的ROV動力學模型[18-19]為

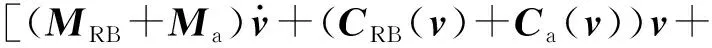
(4)

式中：MRB為ROV的剛體慣性矩陣；Ma為表示慣性水動力的附加質量矩陣；CRB為MRB產生的哥氏力矩陣；Ca為Ma產生的哥氏力矩陣；Dl和Dn分別為黏性水動力的線性和2階非線性水阻尼矩陣；g為恢復力向量；f為環境干擾力及模型參數的不確定量；τ為推進器驅動力向量，τ=[FxFyFzKMN]T。MRB、CRB、Ma、Ca、Dl、Dn和g的完整形式見參考文獻[20-21]，不再詳述。

通過計算機輔助設計軟件Solidworks可計算ROV的質量屬性，其中：質量m=56.914 kg；轉動慣量Ixx=4.849 kg·m2,Iyy=7.373 kg·m2,Izz=11.369 kg·m2,Ixy=Iyx≈0 kg·m2,Ixz=Izx=-0.121 kg·m2,Iyz=Izy=0 kg·m2；重心位置為rg=[xgygzg]T=[0.003 0 -0.014]T，取重心位置為[0 0 0]T。浮心位置rb可通過配置浮力材料進行調節，取rb=[0 0 0.05]T.由ROV的質量屬性，可根據剛體動力學計算得到剛體質量慣性矩陣MRB和剛體科氏力及向心力矩陣CRB，具體表達式見文獻[22]。

2 格子波爾茲曼方法

可通過連續介質描述法和運動論描述法對流體建立數學模型[23]。連續介質描述法假設流體由連續分布的流體微團組成，其內部包含足夠多的流體分子，根據質量守恒定律、動量守恒定律和能量守恒定律推導得出流體運動控制方程，即Navier-Stokes方程。運動論描述法采用統計方法研究大量粒子運動的規律，從微觀角度討論系統的宏觀運動特征。運動論描述法用分布函數f(r,ξ,t)描述流體系統中粒子的密度分布，并將宏觀物理量表示為分布函數的矩。玻爾茲曼方程是運動論描述法的基本輸運方程，其描述了分布函數f(r,ξ,t)的演化規律。LBM可以看作是對連續玻爾茲曼輸運方程的離散求解，其離散輸運方程[24]定義如下：

(5)

LBM的關鍵在于構造粒子間的碰撞模型。典型的碰撞模型為多松弛時間模型，定義如下：

(6)

(7)

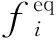
(8)

ωi為保持各向同性而建立的權系數，ρ為宏觀密度，cs為聲速，u為宏觀速度，δ為克羅內克符號，下標α和γ表示方程中向量的不同空間分量。

與標準的多松弛時間模型不同，本文中碰撞模型的散射算子作用在中心矩空間，并通過轉換離散粒子速度和局部宏觀速度，將松弛過程在運動參考系下進行，改善了給定速度集的伽利略不變性和數值穩定性。LBM按照空間維度d和分布函數的數量b進行分類，記為DdQb.本文用于三維仿真的晶格結構為D3Q27(見圖3)。此外，本文采用的湍流模型為大渦模擬，通過直接求解濾波Navier-Stokes方程來計算比網格尺度大的渦，并通過引入亞格子應力模型來考慮小渦對大渦的影響[25]。引入的亞格子應力模型為壁面自適應局部渦流黏性模型，可以提供一致的局部渦流黏度和近壁面行為，更適合對本文復雜水下機器人形成的復雜湍流進行模擬[26]。

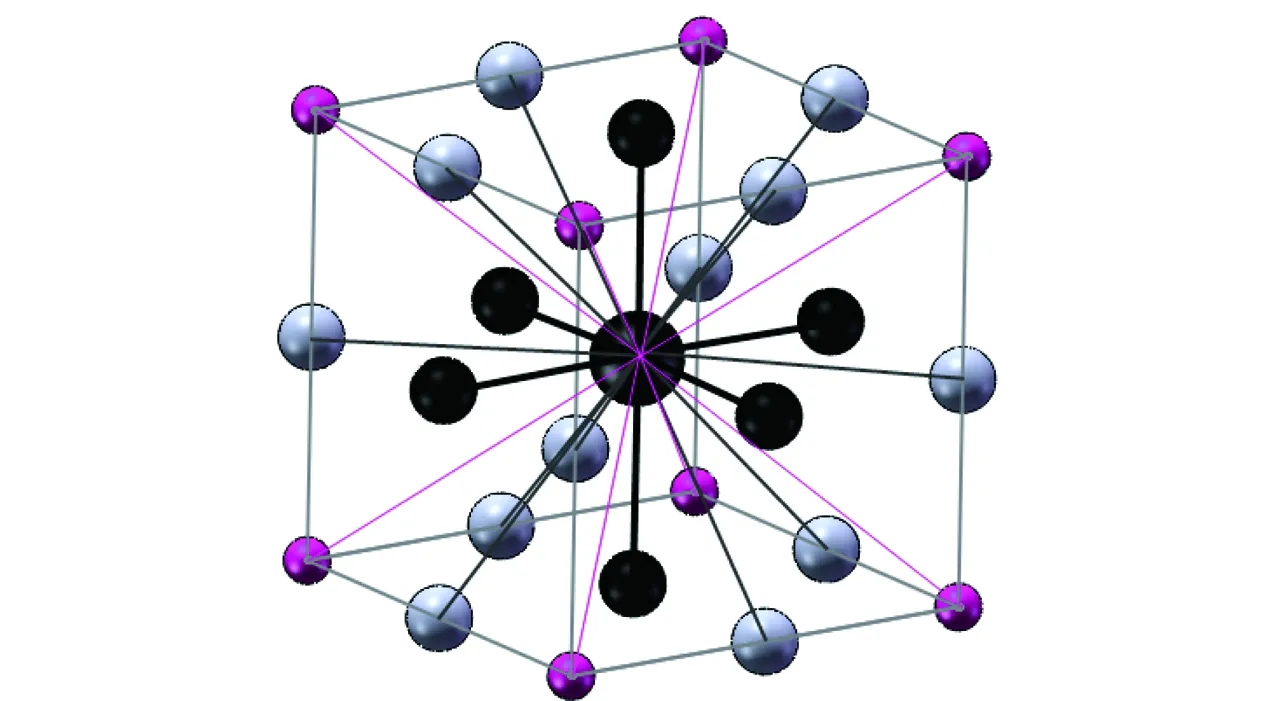
圖3 D3Q27速度離散化的晶格模型Fig.3 D3Q27 lattice model of velocity discretization

3 縱蕩和斜航穩態運動模擬

現有研究已經充分證明RANS方法模擬水下機器人運動的精確性，因此可通過對比穩態縱蕩和斜航運動在基于RANS方程的Fluent軟件和基于LBM的Xflow軟件中的模擬結果，驗證LBM模擬水下機器人運動的可行性。由于基于RANS方程的傳統CFD技術難以實現復雜外形水下機器人的大振幅非穩態運動模擬，故僅對比了穩態運動的模擬結果，這也是本文探究LBM方法模擬水下機器人運動以求水動力系數的原因。

3.1 穩態運動描述和求解器配置

在穩態縱蕩運動模擬中，設置求解域入口流速為U，以相對運動代替ROV的縱蕩速度(見圖4(a))。斜航運動模擬中，將ROV模型固定在長方體求解域中，設置求解域入口流速，并系列地改變漂角β(見圖4(b))。ROV的縱蕩速度u、橫蕩速度v、漂角β和入口流速U的關系可以寫作(9)式：

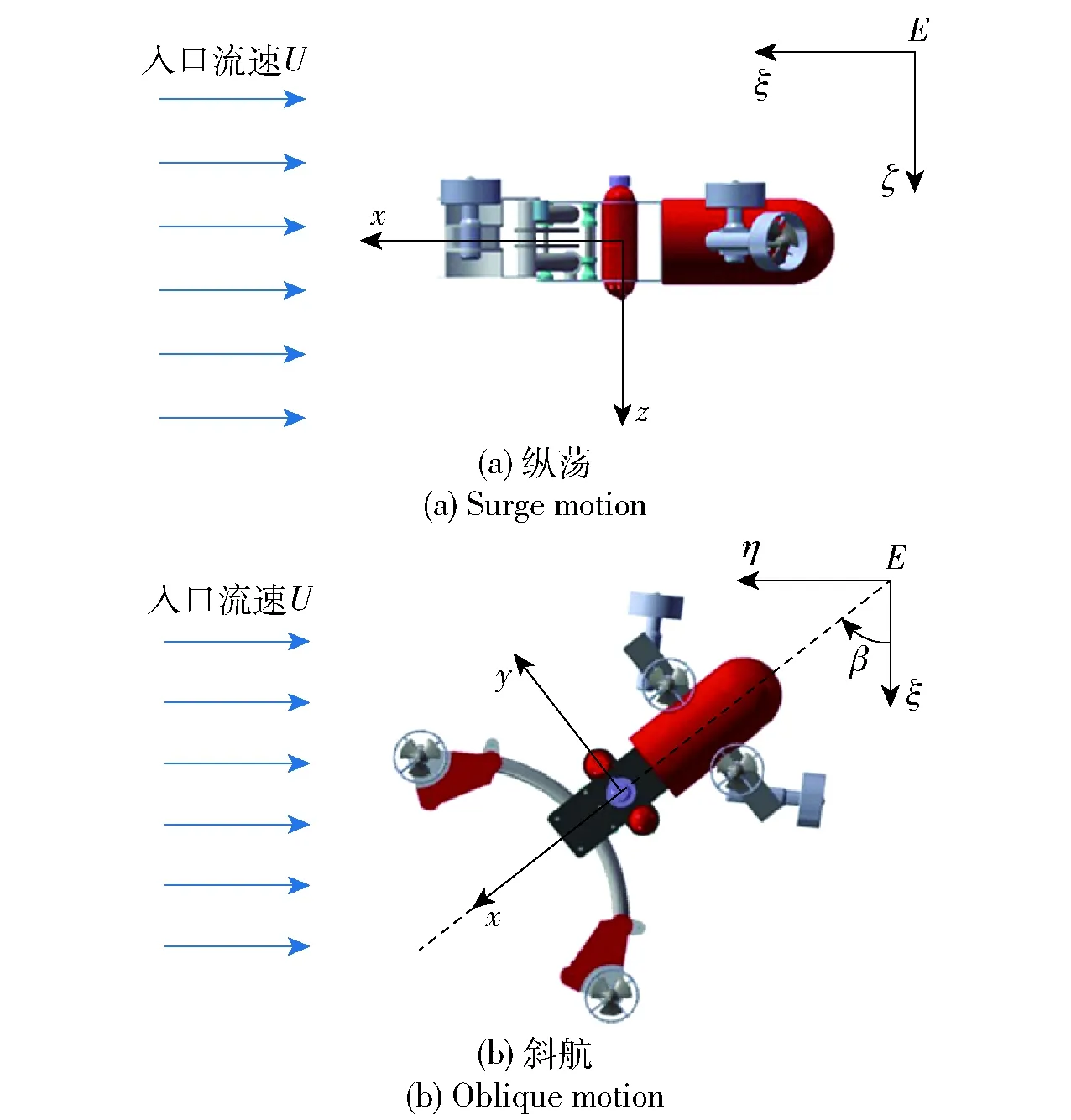
圖4 縱蕩和斜航穩態運動模擬示意圖Fig.4 Schematic diagram of steady-state motion simulation

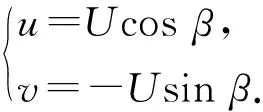
(9)

模擬水池尺寸為長L=10 m，寬W=8 m，高H=6 m，滿足ROV首部迎流大于1.5倍ROV體長、尾部大于3倍ROV體長的要求。穩態縱蕩運動模擬時，求解域入口流速U為0～1 m/s，間隔0.1 m/s；斜航運動模擬時，求解域入口流速為0.8 m/s，漂角β設置為-10°～10°，間隔2°.

Fluent軟件仿真中求解域內劃分尺寸為3 m×2 m×1 m的子流域，以便對近壁面網格進行細化。對求解域進行網格劃分時選擇非結構網格，最終整個流域的網格數量約為240 W，網格結構如圖5所示；湍流模型選擇SSTk-ω模型，壁面函數為對y+不敏感的增強壁面函數，壓力耦合算法選擇壓力隱式算子分割(PISO)算法，求解域入口為速度入口，出口為壓力出口。

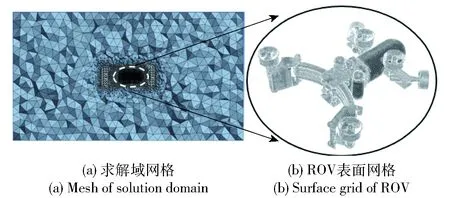
圖5 Fluent軟件仿真中的網格結構Fig.5 Meshing of solution domain in Fluent simulation

Xflow軟件仿真時求解域內劃分兩級子流域，外流域求解尺度為0.1 m：子流域Ⅰ的尺寸為4 m×2 m×1 m，求解尺度為0.012 5 m；子流域Ⅱ的尺寸為6 m×3 m×2 m，求解尺度為0.025 m；ROV的目標求解尺度為0.012 5 m，尾跡求解尺度為0.025 m，并選擇自動設置尾跡細化的閾值。整個求解域共劃分為約670萬單元，求解尺度結構如圖6所示。此外，仿真時間步長為0.01 s，并選擇自適應細化算法。湍流模型選擇壁面自適應局部渦流黏性模型，求解域入口為速度入口，出口為壓力出口，求解域四周壁面設置為自由滑移面，ROV的壁面函數選擇增強壁面函數。

圖6 Xflow軟件中求解域求解尺度結構Fig.6 Resolved scale structure of solution domain in Xflow software

3.2 穩態運動模擬結果與對比

圖7所示為穩態縱蕩模擬中ROV在不同迎流速度下縱向力Fx和斜航運動模擬中不同漂角下橫向力Fy的對比結果。從圖7中可以看出：Xflow軟件和Fluent軟件對ROV所受水動力的預報值基本一致；當縱蕩速度u=1 m/s時，縱向力Fx的相對偏差最大，約為13%；穩態斜航模擬中，當漂角β=±9°時，橫向力Fy的預報值相對偏差最大，約為15%. 圖8和圖9所示分別為斜航運動模擬中漂角β=9°時速度流場和ROV表面壓力云圖的對比結果，從中可以看出形成的流場結構和ROV表面壓力分布計算結果基本一致。選取ROV迎流面中的兩個高壓點(見圖9(a)中的①和②，以及圖9(b)中的③和④)，Xflow和Fluent軟件對該兩點壓力值的計算結果均約為300 Pa，誤差小于10 Pa.

圖7 穩態運動模擬中水動力結果對比Fig.7 Comparison of hydrodynamic results in steady-state motion simulation

圖8 斜航運動速度云圖(β=9°)Fig.8 Contour of velocity field in oblique towing test (β=9°)

圖9 斜航運動ROV表面壓力云圖(β=9°)Fig.9 Contour of ROV surface pressure in oblique towing test (β=9°)

圖8和圖9表明，Xflow和 Fluent軟件對ROV所受水動力的預報誤差很小，流場結構基本一致，驗證了基于LBM模擬水下機器人運動的可行性。此外，由圖8可以看出，ROV所受阻尼力中明顯包含較大的非線性成分，印證了水動力模型中包含非線性水動力系數的必要性。

4 非穩態運動模擬

PMM試驗是約束船模試驗的一種，根據振幅的大小，PMM試驗可以分為LAPMM試驗和小振幅PMM試驗。小振幅PMM試驗只能求取線性水動力系數，LAPMM試驗則可以同時測量線性和非線性水動力系數。

4.1 LAPMM試驗與水動力模型

現有研究中PMM試驗的運動函數多采用近似處理，在運動振幅較小時可以簡化水動力的表達式，降低數據處理和擬合分析的難度。但運動振幅較大時將產生較大的誤差。因此，本節將建立LAPMM試驗的嚴格運動函數，并結合ROV的結構特點推導LAPMM試驗的非線性水動力模型。

4.1.1 非穩態縱蕩運動

非穩態縱蕩運動模擬時，求解域的入口流速設為0 m/s，ROV僅在x軸方向作正弦振蕩(見圖10)。

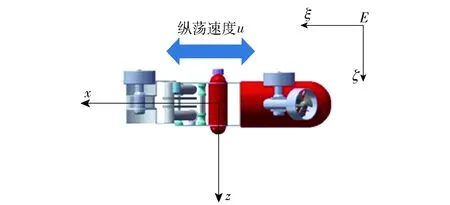
圖10 非穩態純縱蕩運動示意圖Fig.10 Schematic diagram of unsteady-state surge motion

非穩態縱蕩運動模擬可以求得慣性水動力系數Xu(線性黏性水動力系數Xu和2階非線性黏性水動力系數Xu|u|由穩態縱蕩運動計算)。運動函數可以寫作(10)式：

(10)

式中：ω為運動的角頻率(rad/s)；a為縱蕩運動加速度(m/s2)；x0為運動振幅(m)。

4.1.2 純俯仰運動

圖11 ROV純俯仰運動示意圖Fig.11 Schematic diagram of pure pitch motion

(11)

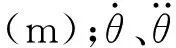
(12)

4.1.3 純橫滾運動

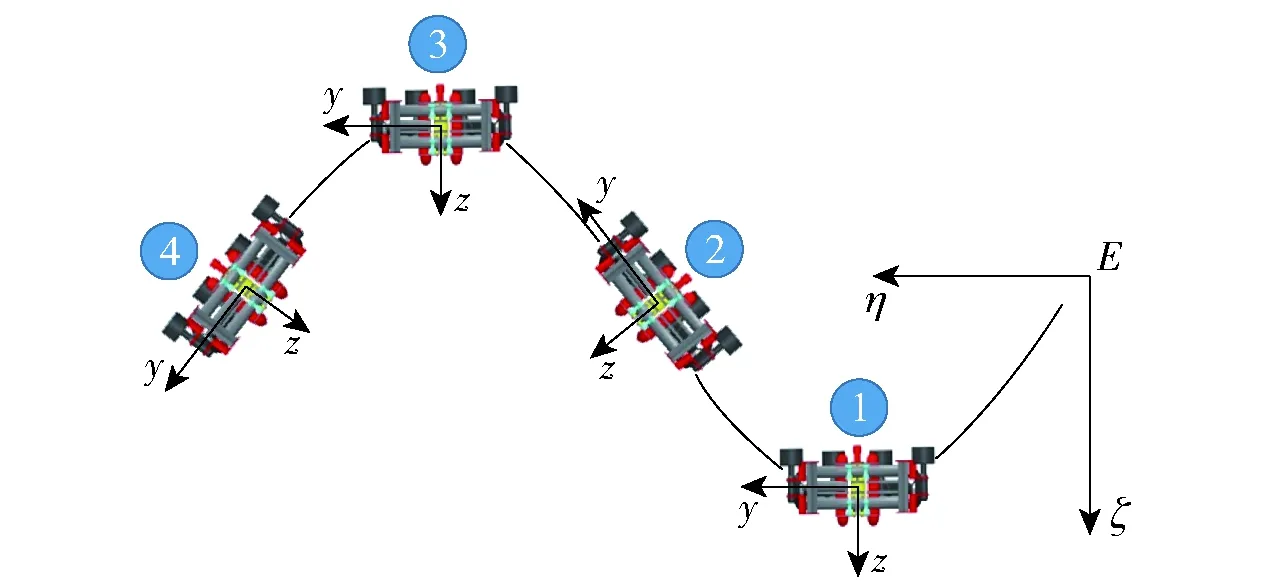
圖12 ROV純橫滾運動示意圖Fig.12 Schematic diagram of ROV pure roll motion

(13)

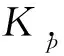
4.1.4 純升沉運動

純升沉運動時，ROV在垂直平面內的運動軌跡為正弦曲線，縱傾角始終為0°，如圖13所示。

圖13 ROV純升沉運動示意圖Fig.13 Schematic diagram of pure heaving motion

運動函數可以寫作(14)式：

(14)

由于ROV結構上下不對稱，Oxy面的迎流面積較大且結構復雜，當深沉速度w方向改變時所受黏性水動力的變化規律差別較大。因此，將垂向力Fzl(w)的線性水動力表達式寫作(15)式：

Fzl(w)=Zww+Z|w||w|，

(15)

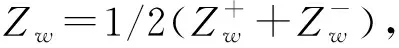
(16)

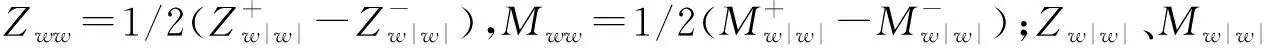
選無霉變的玉米芯，在陽光下曝曬2～3天后，加適當比例的水、石膏粉、石灰粉和多菌靈，拌勻，悶1小時；料的濕度為60%～65%。用稻草作原料，需曬干切成9～12厘米長，用1%石灰水浸一晝夜，撈起后用清水將石灰沖洗干凈，瀝干。拌料時以手握料在指縫中擠出水分不下滴為宜。拌好后將料堆放，悶堆24小時，第2天進行翻堆，并將克霉靈用噴霧器噴灑拌入料中。

(17)

ROV結構的不對稱對其他水動力變化規律也會造成類似影響，但通過仿真檢驗可知其影響較小，因此不再對其他水動力系數進行不對稱性修正。

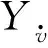
(18)

(19)

Dn=

(20)

4.2 模擬工況與水動力系數計算結果

4.2.1 模擬工況與仿真結果

在Xflow軟件中進行非穩態運動模擬時，求解器配置與求解域的劃分同穩態運動模擬。在6組非穩態運動模擬試驗中，運動振幅均為0.2 m；除非穩態縱蕩實驗在靜水中模擬外(入口流速為0 m/s)，其余入口流速均為0.8 m/s，LAPMM運動的頻率均為0.25 Hz，仿真時間均為5個周期。圖14所示為仿真時間t=16.5 s時的流場云圖(為了使流場更清晰，非穩態縱蕩運動采用了White-Rainbow云圖，其余5組非穩態運動仿真采用Blue-Yellow云圖)。由圖14可以看出，LAPMM運動時ROV的復雜結構使得流場混亂復雜，受力多變，故在該ROV控制算法的研究中，應該考慮水動力模型參數的時變性，關注ROV穩定性的控制。

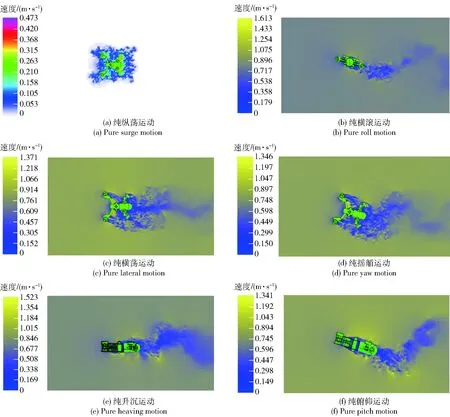
圖14 LAPMM試驗模擬的速度流場云圖Fig.14 Contours of velocity field in LAPMM test simulation

4.2.2 仿真結果的擬合處理

通過CFD運動仿真獲取的是ROV所受水動力和力矩關于時間t的離散值，通過最小二乘法將其對4.1節中所推導的水動力表達式進行擬合，便可獲得相應水動力系數。

圖15～圖19所示為除非穩態縱蕩運動外的5組LAPMM試驗水動力擬合曲線。從圖15～圖19中可以看出，各組PMM試驗水動力模型均可以較好地擬合CFD計算結果。擬合優度系數R2可以表征模型對原始數據的擬合程度，

圖15 純橫蕩運動CFD模擬結果與水動力 模型擬合曲線Fig.15 CFD simulated results and hydrodynamic model fitting curves of pure sway motion

(21)

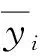
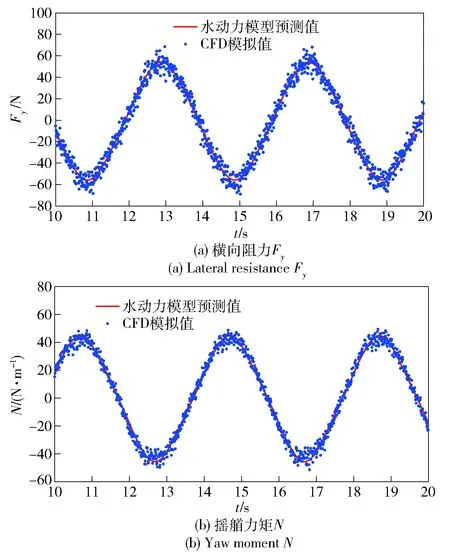
圖16 純搖艏運動CFD模擬結果與水動力模型擬合曲線Fig.16 CFD simulated results and hydrodynamic model fitting curves of pure yaw motion

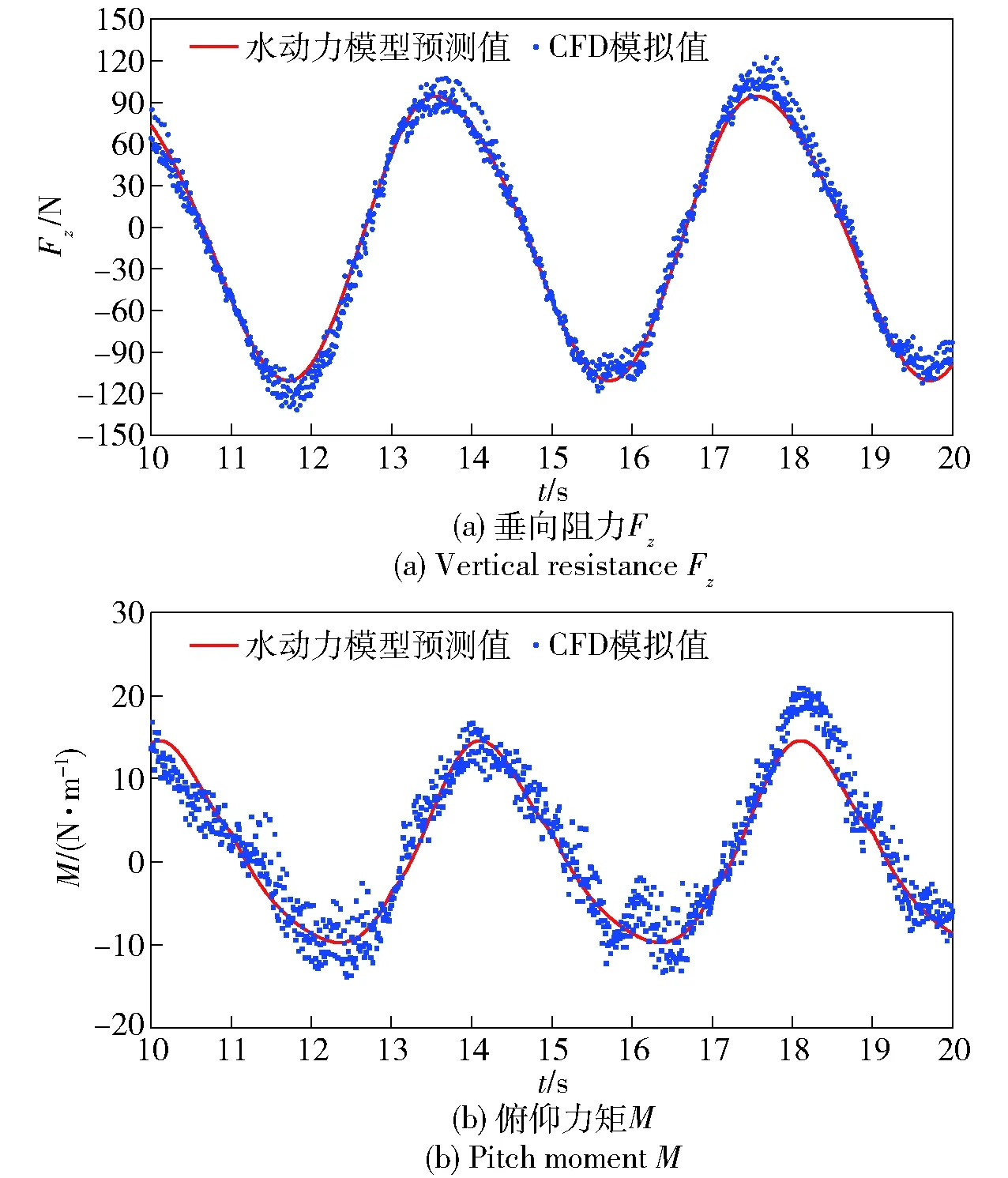
圖17 純升沉運動CFD模擬結果與水動力 模型擬合曲線Fig.17 CFD simulated results and hydrodynamic model fitting curves of pure heaving motion

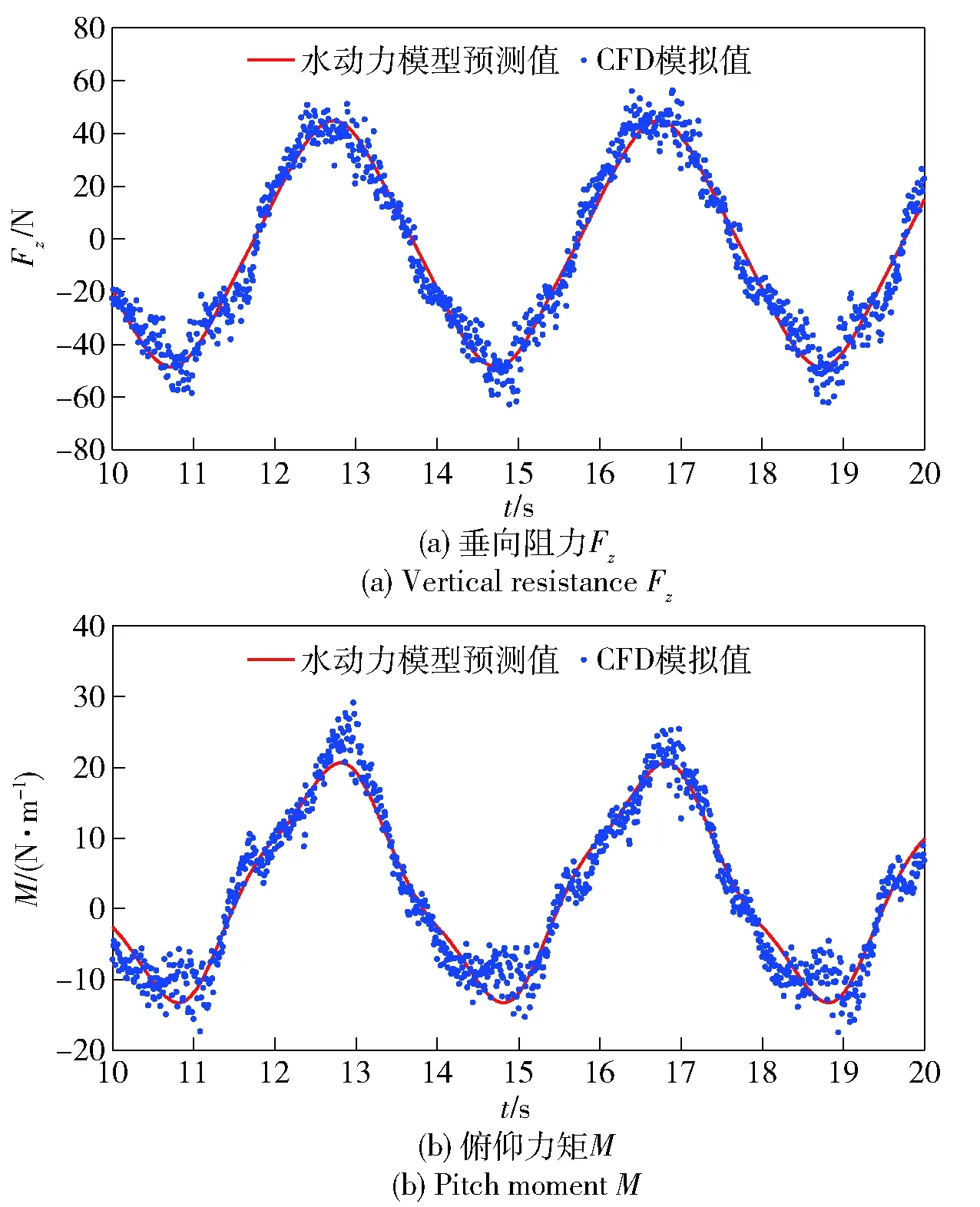
圖18 純俯仰運動CFD模擬結果與水動力模型擬合曲線Fig.18 CFD simulated results and hydrodynamic model fitting curves of pure pitch motion

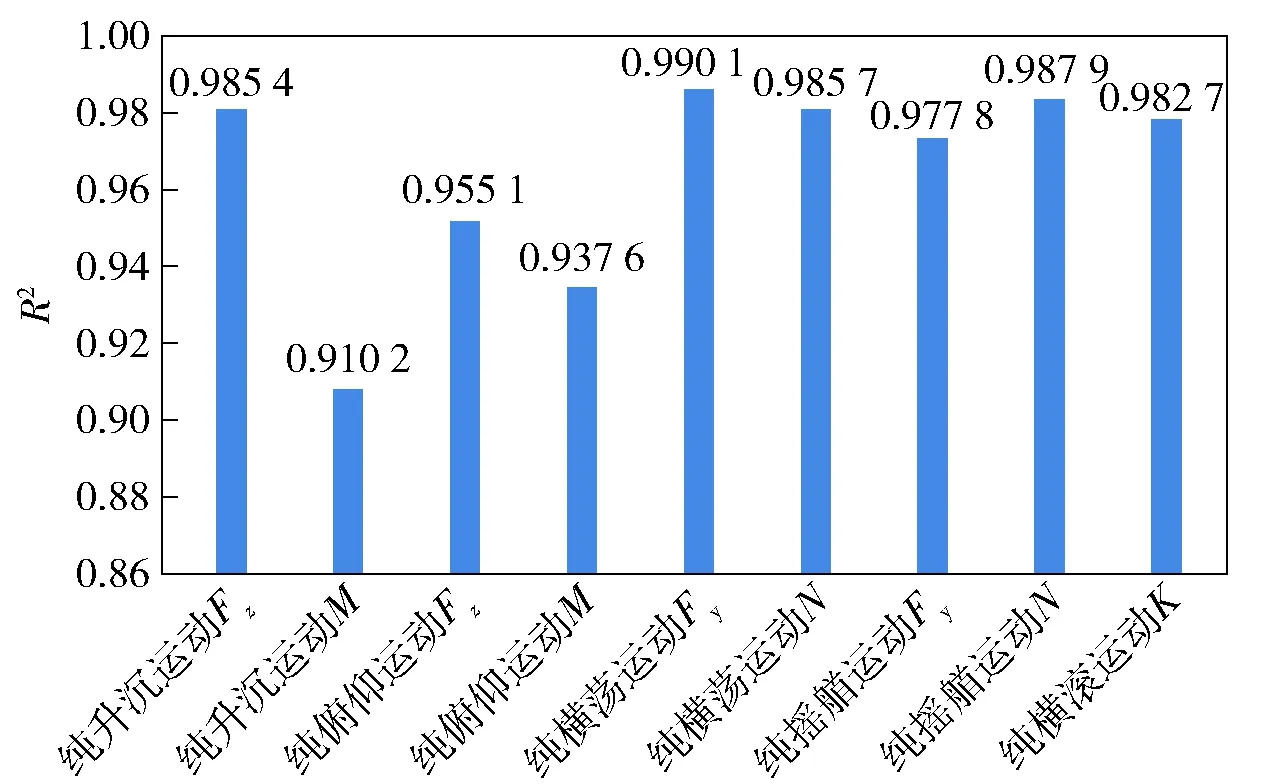
圖20 水動力模型的擬合優度系數Fig.20 Goodness of fit of hydrodynamic models

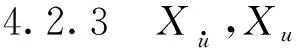
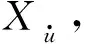
圖21 非穩態縱蕩模擬中水動力Fx與加速度 Fig.21 Longitudinal force Fx and accelerated velocity in unsteady-state surge motion

Fx=Xu|u|u|u|+Xuu.

(22)

(22)式對不同縱蕩速度下的所受黏性水動力變化曲線進行擬合，即可求解得到2階黏性系數和線性黏性系數Xu|u|=-144.801，Xu=-12.24.至此，便求得了(18)式～(20)式中的全部水動力系數，結果如表2所示。表2中水動力系數均做了無因次化處理，各水動力系數單位及無因次化處理過程可參考文獻[21]。

表2 水動力系數的計算結果

4.3 水動力模型分析

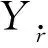
圖與ROV的結構不對稱性Fig.22 Relationship between with ROV structural asymmetry

附加質量矩陣與剛體慣性矩陣同樣會產生科氏力和向心力作用，其與ROV速度向量v的關系用矩陣Ca表示。由已求得的慣性水動力系數可以得到Ca的具體形式如下：

(23)

此外，當垂向速度w方向改變時，與w相關的黏性水動力系數的相對變化率分別如下：

(24)

由上述可見，ROV結構的上下不完全對稱除對垂向線性黏性水動力系數影響較小外，其余3項均超過了50%，表明對于具有不對稱性結構的復雜外形水下機器人，黏性水動力系數的不對稱性修正十分必要。

4.4 與傳統方法的對比

本文的計算平臺配置32核AMD 2990WX 3 GHz處理器，運行內存90 GB；基于RANS方法的仿真軟件為Fluent 19.0，求解器配置16核并行運算；基于LBM的仿真軟件為Xflow 2019x，仿真時16核并行運算。穩態運動模擬中，單次仿真Fluent軟件用時約為6 h，Xflow軟件用時約為5 h. 此外，Fluent軟件仿真計算前需要對求解域進行網格劃分和網格收斂性驗證，盡管已簡化ROV模型，但仍需要對較復雜曲面進行繁瑣的局部網格優化。Xflow軟件在導入模型文件后僅需要對不同求解域設置合適的求解尺度，對曲面復雜性具有更好的容忍度，在保證與Fluent軟件相當精度的情況下，仿真方便快捷，易于實現。

Fluent軟件僅可對小振幅非穩態運動進行模擬，現有研究通過增設穩態運動模擬求解2階及以上非線性和耦合水動力系數的方式，計算周期長。而基于LBM的Xflow軟件對運動振幅沒有限制，極大地縮短了水動力系數計算周期。此外，Fluent等軟件采用動網格技術時，需要編寫用戶自定義函數(UDF)定義ROV的非穩態運動，而Xflow軟件提供了更加簡易的運動函數編輯窗口。

與基于RANS的CFD軟件相比，基于LBM的Xflow軟件雖然擁有更好的并行計算能力，但需要占用更大的數據存儲空間。本文穩態運動模擬中，Fluent軟件單次仿真約占用25 GB存儲空間，Xflow軟件約占120 GB；在Xflow軟件中對大振幅非穩態運動模擬時，設定物理仿真時間20 s，單次仿真數據占用約220 GB存儲空間，仿真計算時長約10 h.

5 操縱性運動仿真

本節將在Simulink軟件中對ROV的直航運動、水平面回轉運動和三維螺旋運動進行仿真。圖23所示為Simulink軟件中搭建的運動仿真系統，通過設置不同的推力向量τ，根據ROV的運動狀態是否為對應標準操縱性運動，來驗證所求水動力系數和運動模型的有效性。圖23中，s為拉普拉斯算子。

圖23 ROV操縱性運動仿真框圖Fig.23 Block diagram of ROV maneuverability motion simulation

5.1 直航運動

直航運動仿真時，僅對ROV施加縱向推力Fx. 圖24所示為ROV航速隨推力的變化曲線。從圖24中可以看出： ROV由靜止開始加速，當所受水動力與推力平衡時速度趨于穩定；隨著縱向推力的增加，ROV的加速階段縮短，符合一般水下航行器的直航運動規律。推進器能提供的最大縱向推力約為200 N，最大航速umax=1.138 m/s. 此外，由于浮力大于重力，ROV同時具有上升速度w，最大縱向推力200 N時，上升速度最終穩定在0.043 1 m/s.

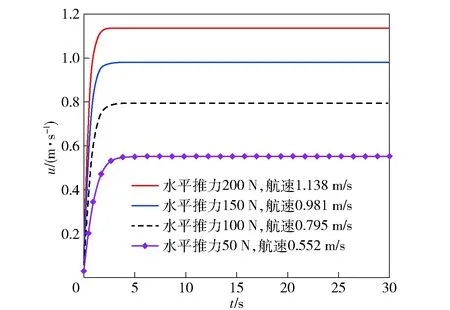
圖24 不同推力作用下ROV的航速Fig.24 Velocities of ROV under different thrust forces

5.2 水平回轉運動

ROV在固定的縱向推力Fx和搖艏力矩N下運動軌跡應為水平回轉運動。為了檢驗平面機動性能，設置搖艏力矩為最大值，即Nmax=8.44 N·m，此時縱向推力Fx=62.367 N. 由于浮力大于重力，ROV實際運動為螺旋上升運動，三維軌跡見圖25(a)，Oxy平面內的投影見圖25(b)。仿真結果表明，ROV進入勻速回轉后，縱向速度u=0.628 m/s，垂向升速w=0.043 m/s，搖艏角速度r=0.13 rad/s，回轉直徑約為D=9.4 m. 可見，所求運動模型在縱向推力和搖艏力矩作用下可實現回轉運動，符合水下航行器水平回轉運動的一般規律。

圖25 ROV平面回轉運動的軌跡Fig.25 Trajectory of ROV in rotational motion

5.3 三維螺旋運動

在水平回轉的基礎上施加垂向推力Fz，則ROV的實際運動應為三維螺旋運動。令垂向推力Fz=100 N，三維軌跡見圖26(a)，水平面和垂直面投影見圖26(b)和圖26(c)。由圖26可知，穩定后ROV的縱向速度u=0.584 m/s，下潛速度w=0.287 m/s，搖艏角速度r=0.214 rad/s，回轉直徑D≈2 m. 可見，所求運動模型可實現預期的三維螺旋運動。但相比水平回轉運動，由于垂向速度較大，ROV受到更大的耦合橫向力Fy和耦合搖艏力矩N，從而具有更大的橫向速度和搖艏角速度，使得回轉半徑明顯縮小。

圖26 三維螺旋運動ROV的軌跡Fig.26 Trajectory of ROV in 3D spiral motion

此外，ROV在螺旋上升時前后受到的垂向水動力不相等，從而形成俯仰力矩。在俯仰力矩作用下ROV俯仰角變化如圖27所示，穩定時仰角θ=32.78°.

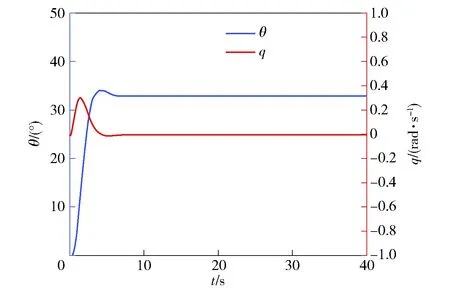
圖27 ROV俯仰角θ和俯仰角速度qFig.27 ROV pitch angle θ and pitch angle velocity q

ROV標準機動性操作仿真的結果，驗證了所求6自由度運動方程的有效性，可以被用于對ROV的操縱性進行預報和控制算法的研究。

6 結論

本文針對一類具有復雜外形的開架式水下機器人，提出一種基于LBM實現LAPMM試驗模擬，以方便快捷地獲取水動力系數的方法。得出如下主要結論：

1)對比LBM和RANS方法在穩態縱蕩和斜航仿真結果發現，縱蕩模擬時縱向力和斜航模擬中橫向力的計算值、ROV表面壓力分布和形成的流場均基本一致，驗證了LBM方法模擬水下機器人運動的可行性。

2)構建了LAPMM試驗嚴格的運動函數和考慮ROV結構不對性的水動力模型。水動力模型的預報值與CFD仿真結果的擬合優度均大于0.9，且水動力系數辨識結果表明由于ROV結構上下不對稱而修正黏性水動力系數十分必要。

3)與基于RANS方法的Fluent軟件相比，基于LBM的Xflow軟件在水動力系數求解中不需要網格劃分，不受水下機器人復雜程度和運動振幅限制，通過LAPMM試驗模擬極大地降低了水動力系數的數值計算難度和求解周期。Xflow雖然具有更好的并行計算能力，但同時需要更大的數據存儲空間。

4)操縱性運動仿真結果符合水下航行器一般運動規律，驗證了所建立6自由度動力學模型的有效性，為后續水下機器人控制算法的研究做好了鋪墊。