基于數據挖掘的光通信系統信息傳輸誤差預測研究
于繼江, 董中平
(中國食品藥品檢定研究院, 北京 102629)
0 引言
隨著通信技術、光傳感技術的不斷發展,產生了光通信系統,相對于其他通信系統,光通信系統的信息傳輸速度快、對環境要求比較低,在許多領域得到了廣泛的應用[1-3]。在光通信系統的實際應用過程中,影響光通信系統性能的因素比較多,如大氣湍流、光反射等,使得光通信系統數據傳輸不穩定,傳輸成功率比較低,難以滿足光通信系統的實際應用要求[4]。信息傳輸誤差預測可以了解光通信系統變化特點,根據預測結果制定一定相應的措施,并進行技術改進,因此光通信系統信息傳輸誤差預測成為了人們關注的焦點[5]。
針對光通信系統信息傳輸誤差預測問題,許多學者進行了深入的研究,當前存在許多有效的光通信系統信息傳輸誤差預測模型[5]。光通信系統信息傳輸誤差預測模型大致可以劃分為兩類[6-8]:一類是傳統模型,主要為線性回歸方法、灰色理論,它們的光通信系統信息傳輸誤差預測建模過程比較簡單,由于傳統模型假設光通信系統信息傳輸誤差是一種線性的變化規律,但現代光通信系統信息傳輸誤差具有一定的時變性,傳統模型的預測偏差比較大,實際應用價值比較低;另一類為現代模型,主要以神經網絡為代表的光通信系統信息傳輸誤差預測模型,它們可以描述光通信系統信息傳輸誤差的時變性,因此光通信系統信息傳輸誤差預測效果得到了明顯的改善。但在實際應用中,神經網絡也具有一定的不足,如學習速度慢,建模過程復雜,因此對光通信系統信息傳輸誤差預測結果有時不可太靠[9]。
由于信息傳輸誤差預測對光通信系統影響十分重要,為提升光通信信息傳輸的成功率,提出了基于數據挖掘的光通信系統信息傳輸誤差預測模型。首先分析影響光通信系統信息傳輸的影響因素,然后引入數據挖掘技術對影響因素和光通信系統信息傳輸誤差之間的變化關系進行建模與分析,最后通過具體的仿真實驗驗證了本文光通信系統信息傳輸誤差預測模型的有效性和優越性。
1 數據挖掘的光通信系統信息傳輸誤差預測模型
1.1 影響因素分析
1.1.1 大氣湍流

(1)

(2)
Δsr=sr(d4 d-1)
(3)
式中,β、sec(φ)分別表示波長和偏角;d表示垂直坐標;sr表示無湍流時的光功率。
1.1.2 背景光模型
光通信系統進行信息傳輸時,通常采用兩級跟蹤探測器,它們分別為粗跟蹤探測器和精跟蹤探測器,設sms、sg分別為信噪比和斜率系數;μbeam為光斑的直徑,那么探測器的等效噪音角U計算式具體如式(4)—式(6)。
(4)
sms=4.14/μbeam
(5)
sg=1.27/μbeam
(6)
粗跟蹤通常情況下采用CCD探測器,其信噪比具體為式(7)。
(7)

精跟蹤通常情況下采用四象限探測器,其信噪比具體為式(8)。
(8)
式中,DEA表示背景光強度;p表示普朗克常數。
背景光譜密度為φ(λ),光通信系統信息接收的口徑和視場角分別為e和α,光通信帶寬為Δf,它們之間存在的關聯性Γ為式(9)。
(9)
1.2 設計光通信系統的信息傳輸誤差預測模型
在光通信系統信息傳輸誤差建模過程中,就是找到一種模型,該模型可以準確描述影響因素大氣湍流、背景光與光通信系統信息傳輸誤差之間的變化關系,從而提高光通信系統信息傳輸質量。相對于人工神經網絡,數據挖掘技術中的支持向量機采用結構風險最小化原則進行建模,其建模精度要高于人工神經網絡,而且預測結果更加可靠。對于樣本集合{xi}∈Rn,i=1,…,l,其中l表示樣本的數量,那么支持向量機建模實際就是通過尋找一個最優超平面將它們分開[11],支持向量機的最優超平面如圖1所示。

圖1 支持向量機的最優超平面
最優超平面描述為式(10)。
ω·x+b=0
(10)
式中,·為點積操作;ω為n維向量;b為最優超平面的偏移量。
對于每一個數據點,盡可能使其與最優超平面之間的距離最大,這樣可以得到一個與式(10)等效的二次優化問題,具體描述為式(11)。
(11)
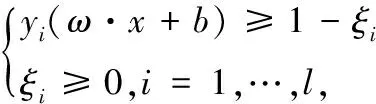
式中,ξ=(ξi,…,ξl)T表示松弛因子;C表示懲罰參數。
為了加快問題的求解效率,對式(11)進行轉換,得到其對偶形式,具體如式(12)。
s.t.
(12)

式中,α表示Lagrange乘子,其應該滿足式(13)。
αi[yi(ω·x+b)-1]=0
(13)
得到支持向量機的決策函數為式(14)。
(14)
對于光通信系統數據,由于光通信系統信息具有非線性變化特點,支持向量機引入核函數對其進行轉換,把非線性變化數據的空間轉換成線性變化數據的空間[12],具體如圖2所示。
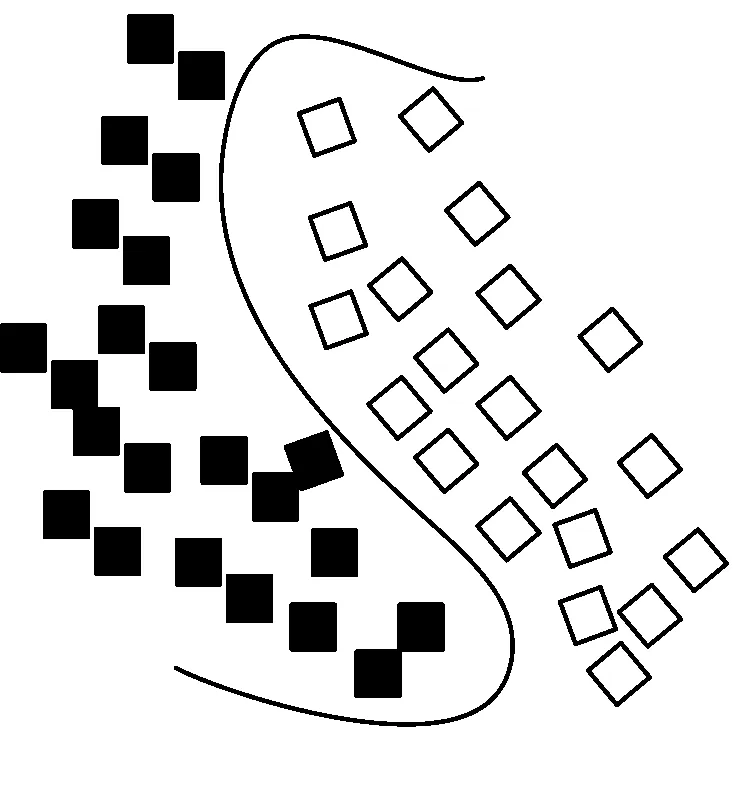
(a) 原始數據分布
對于光通信系統的信息傳輸誤差預測問題,由于引入了核函數,式(12)的對偶形式變為式(15)。
s.t.
(15)

式中,K(xi·xj)表示核函數,具體定義如式(16)。
(16)
式中,σ表示核寬度參數。
2 仿真測試
2.1 測試環境
為了測試基于數據挖掘的光通信系統信息傳輸誤差預測效果,采集一段時間的光通信系統信息作為實驗對象,采用MATLAB工具箱搭建光通信系統信息傳輸誤差預測的測試平臺。
2.2 大氣湍流對光通信系統性能影響的測試
在不同大氣湍流條件下,測試其對光通信系統性能的影響,具體如圖3所示。
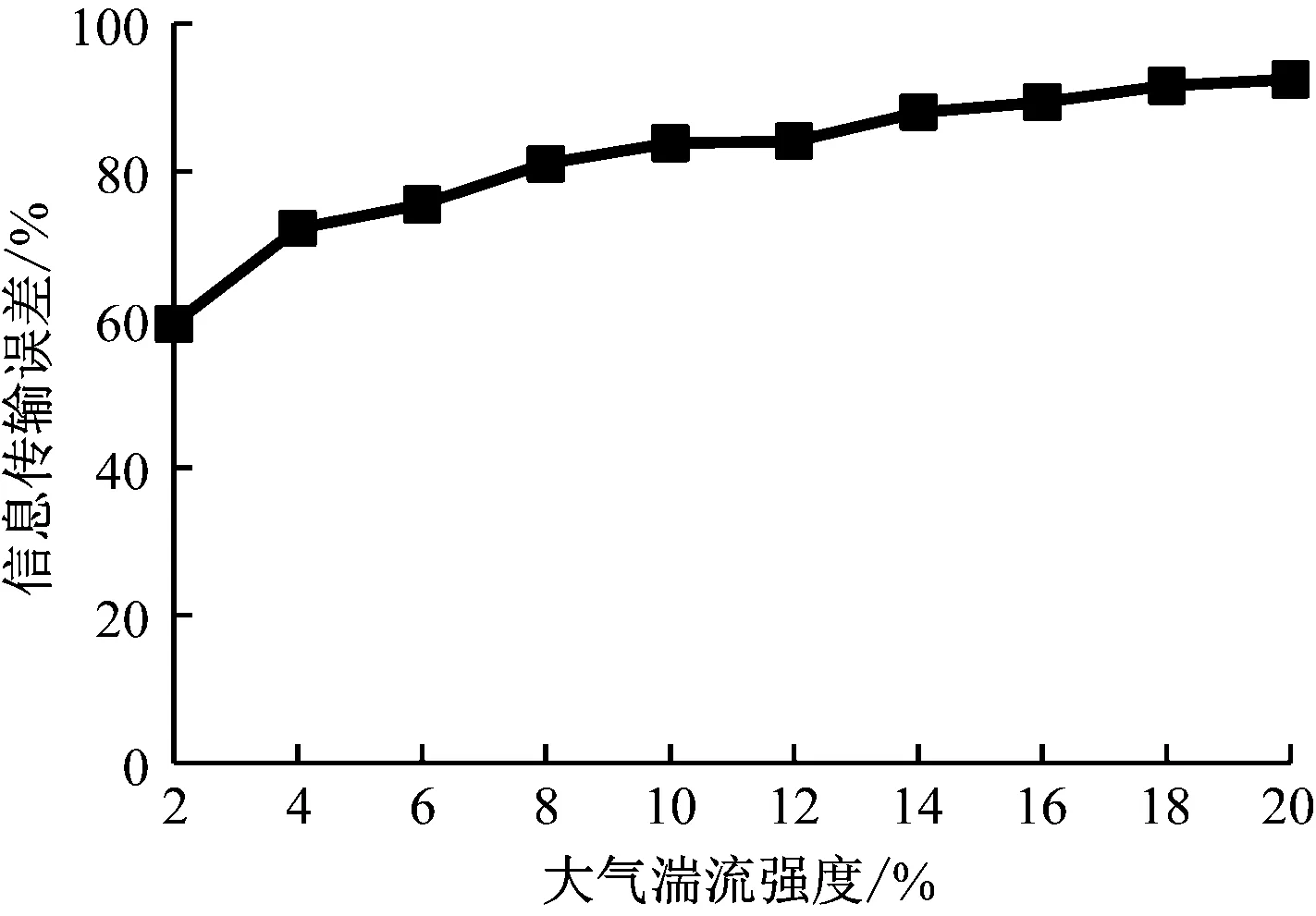
圖3 大氣湍流對信息傳輸誤差影響程度
對圖3的信息傳輸誤差進行分析可以發現,隨著大氣湍流的值不斷增加,信息傳輸誤差呈上升趨勢,因此在實際應用中盡可能使大氣湍流強度越小,以獲得理想的光通信系統信息傳輸效果。
2.3 背景光對光通信系統性能影響的測試
在不同背景光條件下,測試其對光通信系統性能的影響,具體描述如圖4所示。

圖4 背景光對信息傳輸誤差影響程度
對圖4的信息傳輸誤差進行分析可以發現,隨著背景光值不斷增加,信息傳輸誤差同樣呈上升趨勢,但是其影響程度不如大氣湍流,這表明本文選擇背景光、大氣湍流兩種影響因素對光通信系統信息傳輸誤差進行建模的思想是正確、有效的。
2.4 光通信系統信息傳輸誤差預測效果分析
為了進一步驗證數據挖掘的光通信系統信息傳輸誤差預測的優越性,選擇BP神經網絡的光通信系統信息傳輸誤差預測模型(BPNN)、多元線性回歸的光通信系統信息傳輸誤差預測模型(MLR)在相同實驗環境下進行對比測試,選擇光通信系統信息傳輸誤差預測精度作為評價指標,預測精度計算式具體為式(17)。
(17)
式中,Tvalue和Pvalue分別表示實際傳輸誤差與預測誤差。
每一種模型均進行5次光通信系統信息傳輸誤差預測建模,統計每一次預測精度,得到結果如表1所示。
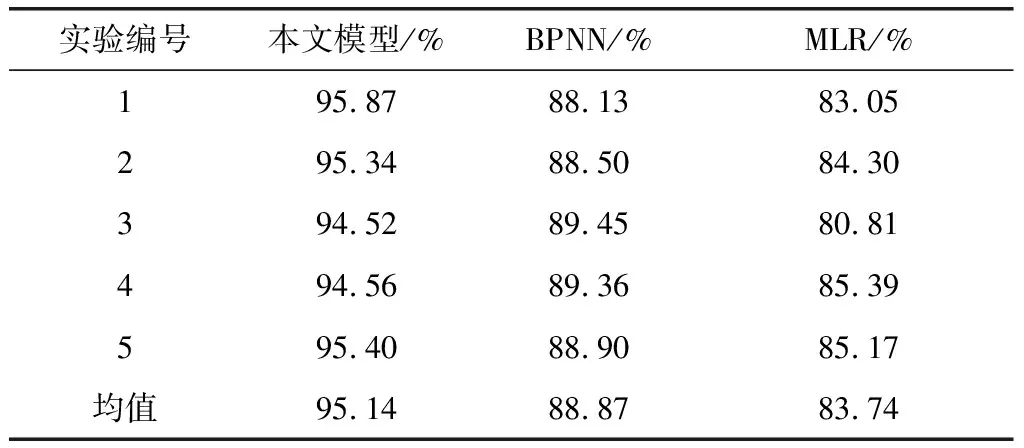
表1 光通信系統信息傳輸誤差預測精度對比
對表1的光通信系統信息傳輸誤差預測精度進行分析可以發現,本文模型的光通信系統信息傳輸誤差預測精度均值為95.13%,而BPNN和MLR的光通信系統信息傳輸誤差預測均值分別為88.87%和83.74%,由此可見本文模型降低了光通信系統信息傳輸預測誤差,可以改善光通信系統信息傳輸效果,具有十分明顯的優越性。
3 總結
針對當前光通信系統信息傳輸誤差預測建模過程中存
在的一些難題,結合光通信系統信息的變化特點,以提高光通信系統信息傳輸誤差預測精度,提出了基于數據挖掘的光通信系統信息傳輸誤差預測模型,選擇大氣湍流、背景光作為影響因素,將它們作為支持向量機的輸入,信息傳輸誤差作為支持向量機的輸出,通過支持向量機進行訓練和學習,對輸入和輸出之間的關系進行擬合,測試結果表明,大氣湍流對光通信系統信息傳輸效果的影響程度要高于背景光,對照實驗證明了本文模型的光通信系統信息傳輸誤差預測精度要明顯優于當前其他模型,可以提升光通信系統信息傳輸質量,具有十分廣泛的應用價值。

