基于向導點法反演水文地質參數

何金沙，李春光，，呂歲菊，楊佩瑤，黃傳霽

（1.寧夏大學土木與水利工程學院，銀川750021；2.北方民族大學數值計算與工程應用研究所，銀川750021）

0 引 言

水文地質參數在地下水資源評價、數值模擬、開發利用等方面具有十分重要的作用。地下水數值模型所能承載的某一種參數的最大維度等于該模型的網格剖分數目，大多數情況下觀測數據包含的信息有限，直接對所有網格的參數進行反演具有一定的難度。而參數化方法通過某種特定數學關系簡化實際參數組，無需對數值模型單個網格進行參數估計，僅反演簡化后的參數組，再對已估參數點進行插值，從而得到含水層參數的估計場。傳統的地下水參數分區人為的將模型區域劃分為若干個小分區，每個分區用一個參數表示，在參數估計過程中只反演這些分區的參數的值[1]。然而這種區域的劃分往往帶有一定的主觀性，不能很好地反映真實參數場的空間結構。

近年來，隨著數值模擬技術的發展，向導點法成為求解非均質水文地質參數的一種新途徑。向導點法通過在模型區域中布設一定數量的點，估計這些點處的參數值并進行插值以獲得整個參數場的估計場。該方法與地統計學的結合可有效克服傳統分區的缺點[2]，獲得的參數場更符合真實情況[3]。在先驗信息（如地質資料）豐富的情況下，可以依據當地的地質情況布置觀測井與向導點，獲得更加精確的水文地質參數場。例如Young S[4]基于Edwards-Trinity 高原和Pecos 峽谷的地質資料，通過在不同研究區域內均勻布置向導點，求解了水文地質參數。在缺乏先驗信息的情況下，以往的研究都是將向導點與觀測井均勻布置在整個研究區域。例如姜蓓蕾[5]使用該種布置方式，討論了向導點個數對反演結果的影響。這種布置方式雖然被廣泛采用，但是學者們并未對其展開深入研究，主要原因是向導點的數量關系可以定量描述，但觀測井與向導點位置描述起來不是十分方便。本文采用觀測井與向導點分布范圍占研究區面積的比例來描述兩者的位置關系，該方法可以不受區域面積和形狀影響，不僅對于規則研究區域有效，還可以運用到不規則的研究區域。在此基礎上，通過理想算例研究了觀測井與向導點不同分布范圍以及滲透系數場初值對反演結果的影響，為向導點法在水文地質參數反演中的推廣提供了依據。

1 計算程序與算法

1.1 向導點法

向導點法起源于地質統計學，通過在模型區域內布設一定數目的點(向導點)，反演這些點處的參數值，再經過克里金插值得到整個參數場的估計場[6]。向導點法反演參數場的主要步驟見圖1，其中Modflow 程序調用次數表示地下水模型Modflow.exe 運行次數，優化迭代次數等于PEST 程序循環次數。向導點法用于解決高維不適定問題，即向導點個數要大于觀測井個數[7]。在先驗信息不足的情況下，向導點應均勻分布在研究區內。此外，在參數估計中不同位置的觀測井對目標函數的貢獻不同，觀測井應盡可能的包含更多的含水層信息。如果初始參數向量與最優參數向量相差較大，參數估計問題陷入局部最優，難以找到目標函數的全局最優解。

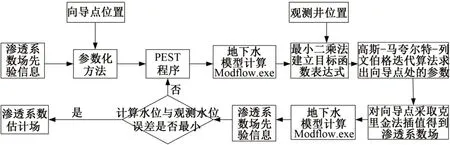
圖1 向導點法反演參數場的主要步驟流程圖Fig.1 Flow chart of the main steps of inversion of parameter field by the pilot point method

1.2 Gauss-Marquardt-Levenberg 迭代算法

大多數情況下，模型參數與觀測值之間的關系都是非線性的，在求解過程中必須將非線性模型線性化。本文主要研究滲透系數與觀測水位之間的關系，假設二者之間的非線性關系用函數c=M(b)表示，該函數可看作是n維參數空間映射到m維觀測空間[函數c=M(b)所有待估模型參數的導數必須連續可導]。某一初始滲透系數向量b0對應的模型觀測水位向量為c0，即：

任意向量b與其對應向量c的關系，可用如下泰勒展開式表示：

當b-b0足夠小時，可以忽略式(2)中二階以上的高階項，從而簡化為：

其中矩陣J是函數c=M(b)在b0處的雅克比矩陣(Jacobian Ma?trix)，共有m行n列，每行的元素為對應的待估模型參數的偏導數。

目標函數是模型計算水位與實際水位之差的平方和，而參數估計過程實際上是最小化目標函數的過程。假設n階對角矩陣Q的第Z個對角元素表示的是第i個實際觀測值的權重W的平方，cr表示實測水位向量，則非線性模型參數反演問題的目標函數表示為：

目標函數需要反復迭代更新雅可比矩陣J與參數向量b以使b-b0到達最小，定義參數更新向量b-b0為u，則u可表示為：

假定殘差向量r=cr-c0，則式(5)可寫為：

若目標函數Φ的梯度為g，則向量

在公式(6)中加入Marquardt參數，使估計初期參數更新向量u靠近向量g的反方向，u的表達式變為：

式中：α為Marquardt 參數；I為n階單位矩陣；梯度向量g又可定義為g=-2JTQr。

高斯-列文伯格-馬夸爾特迭代算法是在高斯—牛頓迭代法的基礎上進行改進而來的，用于求解廣義非線性加權最小二乘最小化問題[8]。該方法在每次迭代過程中，通過對待估模型參數進行求導將非線性模型線性化，同時更新參數向量，計算新的目標函數，不斷重復迭代優化過程，直到目標函數滿足要求。

1.3 PEST程序

PEST( 全稱Parameter Estimate) 是由澳大利亞Water Numerical Computing 咨詢公司開發的用于參數估計與不確定性分析的程序。PEST 程序第一個版本誕生于1994年，最初只具有非線性參數估計功能，經過20 多年的發展，目前已經具備了強大的正則化功能與不確定性分析功能。PEST 程序使用高斯-列文伯格-馬夸爾特非線性參數估計方法，相比于其他非線性參數估計方法，該法可以在有效估計參數的同時節省大量運行模型的次數。最新版本的PEST 程序支持向導點法并且帶有專門針對地下水問題的程序集，因此可以很方便地與Modflow等地下水模型進行藕合使用。

參數估計的目的是找到一個滲透系數向量，即滲透系數估計場，使得模型計算水位最大限度地擬合實際觀測水位。為準確評估先驗信息精度與反演精度，采用RMSE（Root Mean Square Error，均方根誤差）作為衡量初始滲透系數場和滲透系數估計場（與實際滲透系數場）精度的評判標準，公式如下：

式中：n為參數個數；yt和ya分別表示參數的真實值和模型計算值；RMSE的值越小反演精度越高。

2 理想算例

本文采用確定性地下水數值模擬軟件Visual Modflow[9]建立了一個二維承壓含水層數值模型，如圖2所示。假定該模型中含水層水平等厚，平面是邊長為1000m 的正方形，底板高程為0 m，頂板高程為5 m，北邊界為定水頭邊界，其余邊界為隔水邊界，上部接受0.000 5 m/d 的面狀補給，模擬計算時間為365 d。通過克里金指數變異函數插值出地下水滲透系數對數場，作為實際滲透系數場（注：高斯變異函數在PEST 程序中運行結果會超出向導點值設定上下限，不建議使用[10,11]）。在研究區布置36 口井，作為地下水水位觀測井。由于向導點法中參數反演屬于不適定問題，向導點數要大于觀測井數，因此在研究區內布置了64個向導點。

圖2 理想算例中真實滲透系數場(log K)Fig.2 The real permeability coefficient field in the ideal case(log K)

在實際滲透系數場中選擇16 個點，這些點的滲透系數值是已知的，對其進行普通的克里金插值獲得初始滲透系數場（見圖3），其與實際滲透系數場之間的RMSE記作R1，表示先驗信息精度，此時的模型計算水位與實際水位還有較大差距。經過PEST 程序參數反演后，模型計算水位能夠最大限度地擬合實際水位[12]，得到的參數場稱為滲透系數估計場，與實際滲透系數場之間的RMSE記作R2，表示反演精度。模型計算水位與滲透系數值取自系統，誤差范圍為0.001。

圖3 16個點(三角形)位置與初始滲透系數場(log K)Fig.3 The location of 16 points(triangles)and the initial permeability coefficient field(log K)

3 分析與討論

為了研究觀測井、向導點分布范圍以及不同滲透系數初值對反演結果的影響，結合理想案例，分別設置不同分布范圍的觀測井和向導點模型及不同初值的初始滲透系數場模型，并對反演結果進行分析與討論。

3.1 不同觀測井分布范圍反演結果分析

在參數估計中，觀測井所包含的含水層信息越多，模型反演精度越高。為了研究不同觀測井分布范圍對反演結果的影響，將64 個向導點均勻分布在整個研究區，36 口觀測井均勻布置在占研究區總面積16%、36%、64%、81%和100%的正方形范圍內（如圖4所示），正方形中心與研究區域中心重合。通過PEST 程序對初始滲透系數場進行反演求解，限于篇幅，僅給出觀測井分布范圍占研究區總面積16%、81%和100%的結果，分別見圖5～圖7。可以看出，當觀測井布置范圍適當時，反演結果較準確地反映了真實滲透系數場的空間分布，說明向導點法能夠有效求解地下水反演中的不適定問題。

圖4 觀測井分布范圍示意圖Fig.4 Schematic diagram of the distribution range of observation wells

圖5 分布范圍為16%滲透系數估計場（log K）Fig.5 The distribution range is 16%of the estimated field of permeability coefficient(log K)

圖6 分布范圍為81%滲透系數估計場（log K）Fig.6 The distribution range is 81%of the estimated field of permeability coefficient(log K)

圖7 分布范圍為100%滲透系數估計場（log K）Fig.7 The distribution range is 100%of the estimated field of permeability coefficient(log K)

觀測井不同分布范圍情景下反演結果見表1。盡管初始滲透系數場與真實滲透系數場之間的R1 很小，甚至小于R2，但仍然不采用初始滲透系數場直接作為滲透系數估計場。這是因為本次理想案例中真實滲透系數場數據是已知的，僅作為參照場，可以計算出R1與R2值。而實際工程中的真實滲透系數場是未知的，擬合地下水水位反演后的也只是滲透系數估計場，無法計算R1與R2的值。

表1 不同觀測井分布范圍反演結果Tab.1 Inversion results of distribution range of different observation wells

觀測井中實際水位與計算水位的RMSE變化區間為2.36×10-7～6.35×10-4，表明水位擬合十分良好。當觀測井分布范圍為16%時，R2值為0.447，反演效果最不理想；當觀測井分布范圍從16%增加到64%時，對應的R2 值依次減小(0.447>0.156>0.069)，說明隨著觀測井分布范圍增加，獲取的含水層參數信息增加，反演精度逐漸提高；當分布范圍為81%與100%時，對應的R2 值為0.056、0.057，再次說明觀測井分布范圍增加到一定程度時，獲取的含水層信息不再有太多變化，反演結果能夠有效反映滲透系數場的空間分布，反演精度逐漸趨于穩定。

3.2 不同向導點分布范圍反演結果分析

為了研究不同向導點分布范圍對參數估計的影響，將36口觀測井均勻分布在整個研究區，而64 個向導點均勻分布在占研究區總面積的16%、36%、64%、81%和100%正方形范圍內，正方形中心依然與研究區域中心重合。

向導點不同分布范圍情景下反演結果見表2。地下水位觀測值與計算值的RMSE位于3.73×10-7～5.53×10-7之間，研究區水位擬合良好。當向導點分布范圍為16%、36%，64%時，對應的R2值依次減小(0.194>0.065>0.045)；而當向導點分布范圍為81%、100%時，R2 值分別為0.052、0.057，雖比64%對應的R2值0.045大，但增加幅度很小，基本保持穩定，說明增加向導點分布范圍同樣可以獲得更高精度的滲透系數場。當向導點集中在部分區域時，獲取的滲透系數參數信息較少，導致目標函數在負方向上步長變小，下降速率變慢。在本次模擬中，雖然目標函數初始值相同，但步長越小，達到目標函數要求所調用Modflow程序和優化迭代的次數就會越多[13]。

表2 不同向導點分布范圍反演結果Tab.2 Inversion results of distribution range of different guide points

在參數化方法中，樣本點的選取對參數反演結果影響很大，在研究區域內，抽樣應該具有無偏性和一致性。當分布范圍較小時，抽樣數據集中在較小的范圍，與真實滲透系數場和觀測數據差距較大，無法代替整個參數組與觀測組。隨著向導點與觀測井分布范圍的增加，選擇的樣本區域擴大，盡管選擇的樣本數量不變但有效樣本數增加，反演精度提高，R2 逐漸減小。隨著分布范圍接近整個研究區域，有效樣本數目變化不明顯，R2值基本保持穩定。

3.3 不同滲透系數場初值反演結果分析

為研究滲透系數場初值對反演精度的影響，將36 口觀測井與64 個向導點分別均勻布置在整個研究區域內，在16 個已知滲透系數值點對數值的基礎上增加0%、-10%、-20%、30%、50%、100%，重新進行克里金插值得到不同初值的初始滲透系數場，對應R1 值分別為0.053、0.151、0.297、0.466、0.768、1.527。

在此基礎上進行反演，結果如表3所示。可以看出，觀測水位與計算水位RMSE 值在3.33×10-7～4.71×10-7范圍內，研究區水位擬合良好。R2 與R1 呈正相關，R1 值越小，R2 值也越小，擬合精度越高；反之，擬合效果越差。這是因為對于非線性問題，如果初始參數向量b0在參數空間中的位置與使目標函數最小化的最優參數向量b的位置相差較大時，參數估計問題容易陷入局部最優，使目標函數全局最小難以實現。同時由于模型要求b-b0盡可能小，目標函數的最小化需要反復迭代更新雅可比矩陣與向量b，即模型調用Modflow 程序與優化迭代的次數也會隨著R1 的增加而增加。因此，初始參數向量b0越接近真實情況，反演精度越高[14]。

表3 不同初值的初始滲透系數場反演結果Tab.3 Inversion results of initial permeability coefficient field with different initial values

4 結 論

本文通過PEST 程序與地下水流模擬軟件Modflow 耦合，對設定的理想算例進行滲透系數的高維反演，研究了向導點與觀測井分布范圍、滲透系數場初值對反演水文地質參數的影響，得出以下結論：

（1）向導點法是一種有效反演水文地質參數的方法，在參數反演應用方面具有較高的優越性，避免了人為概化分區的局限性，反演結果能較好地反映參數場的非均質性和空間結構。

（2）隨著觀測井分布范圍的增加，參數反演精度逐漸提高并最終達到穩定，在觀測井分布范圍接近整個研究區域時達到最高。

（3）隨著向導點分布范圍增加，反演精度逐漸提高并趨于穩定，調用Modflow 程序和優化迭代的次數變少。向導點分布范圍覆蓋整個區域時，模型調用次數與優化迭代次數最少，此時該種布置方式較為簡單，推薦實際工程中使用。

（4）采用向導點方法反演參數時，初始參數信息越接近真實情況，反演精度愈高。