挖掘機自主挖掘軌跡規劃方法研究

謝中東

（長安大學工程機械學院，陜西 西安 710064）

0 引言

在現代社會中，挖掘機是用來執行工業工程任務的重要設備，其主要使用領域是建筑、工業、運輸、交通等。隨著社會的發展，一些特殊環境也開始使用挖掘機作業，如深海挖掘、探索宇宙等。挖掘機在作業過程中往往都是重復且連續的作業，同時操作員對操作挖掘機的作業環境要求較為嚴格，而大部分作業環境會伴隨著噪聲、塵土和一些其他的因素的影響。因此，對于操作員的操作水平以及心理素質要求也越來越高。并且一些特殊的工作環境可能對操作員的身體產生危害，導致操作員無法直接進入。再者，培養熟練的操作員去完成高水平、高質量的作業任務需要耗費較多的時間和金錢。因此，國內外越來越多的學者開始關注挖掘機的智能化挖掘。同時，隨著工業的不斷發展，挖掘機智能化、自動化挖掘有了較好的發展條件。液壓挖掘機是經濟建設中最常用的工程機械之一，國內外學者針對挖掘機的機器人化進行了多方面的研究[1-2]。實現挖掘機自動化作業是非常必要的，因此，必須解決挖掘機的軌跡規劃問題。朱世強等提出的七次樣條曲線插值方法，能夠避免振動問題，但計算復雜，效率比較低[3]；Gao D等利用多項式插值方法在關節空間對機械臂進行軌跡規劃，并通過ADAMS軟件實現仿真驗證[4]；劉宇等以三次NURBS曲線插值關節位置，得到滿足物理約束的時間、平滑性綜合最優的軌跡曲線[5]；管成等提出基于五次NURBS曲線的時間最優軌跡規劃[6]，通過權因子適時調整挖掘軌跡，但是NURBS曲線的求導計算式煩瑣，編程復雜且求解效率低[7]。

本研究以某型挖掘機為研究對象，在關節空間對自主挖掘過程分別進行三次樣條曲線和五段五次多項式插值，并對軌跡規劃得出的曲線進行比較，以此得出相對性能更優的軌跡規劃方法。

1 挖掘機的運動學分析

1.1 挖掘機工作裝置D-H模型的建立

挖掘機工作裝置包括動臂、臂和鏟斗接頭。為了實現自主操作，鏟斗應與地面保持一定角度，以實現水平挖掘或自主開挖溝。當不考慮旋轉時，工作裝置的尖端軌跡由三個關節的運動組成，可以將其視為平面三桿操縱器。該機械手由四個連桿和三個旋轉關節串聯而成，固定在挖掘機器人的基座上。本研究采用組合運動方式進行了挖掘機的軌跡規劃。動臂液壓缸、斗桿液壓缸和鏟斗液壓缸相互配合。挖掘動作由繞動臂的鉸接點旋轉的臂來驅動，并且動臂液壓缸也被導引以控制運動軌跡。在挖掘機的軌跡規劃中，根據機器人理論，將挖掘機的工作裝置建立在D-H坐標系中，求得逆運動學的解，如圖1（a）所示。其中，θ1、θ2、θ3、ζ分別為動臂關節變量、斗桿關節變量、鏟斗關節變量以及鏟斗尖端與地面夾角。挖掘機運動學模型，Matlab挖掘三關節仿真圖，如圖1（b）所示。

圖1 挖掘機的挖掘三關節

1.2 運動學的逆解

筆者研究了具有三個自由度的挖掘機，這是具有冗余自由度的機器人的重要基礎模型之一。首先，根據D-H方法建立工作裝置的運動學模型，并進行正向和逆向運動學分析。在正向運動學解決方案中，每個關節角度的工作裝置和連桿的長度是已知的，并且鏟斗尖端相對于基本坐標系的位置和姿勢可以解決。在挖掘工作中，挖掘控制點在笛卡爾坐標系中描述，軌跡在關節空間中進行規劃。因此，要實現這一過程，必須求得逆運動學的解，即將挖掘控制點的位姿坐標轉換為關節空間中關節的轉角。逆解的計算在軌跡規劃過程中非常有意義。它包含自動控制端的變量，并為控制系統提供數據信息。然而，通常多個冗余機器人的運動學逆解相對困難的，逆運動學結果可能包含不確定數量的解。求解逆解的主要計算方法有三種，分別為解析法、迭代法、幾何法。由于解析法在求解過程中需要進行矩陣逆乘運算，當所需要求逆解的機器人是多自由度時，此法得到逆解更加簡單。而迭代法通過迭代收斂得到的唯一解有可能是錯誤的解，且其收斂速度難以控制。幾何法適用于自由度較少、能夠進行直觀轉換計算的情況。本研究中的挖掘機結構比較簡單，自由度較少，因此，這里選取幾何法求得其逆解。通過幾何推導圖1（a）得到的位置。其中，為O2的長度。

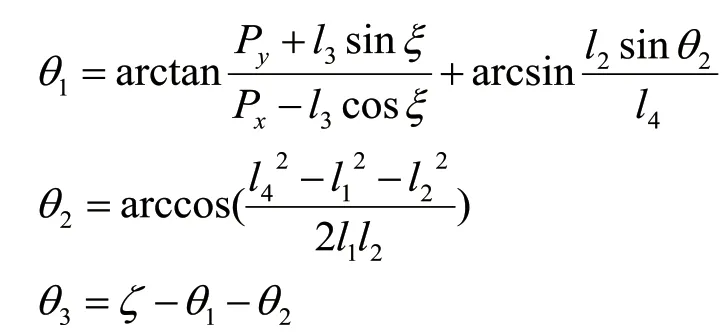
1.3 工作空間

為了確保鏟斗尖端的預期目標工作空間完全包圍實際的運動空間，對挖掘機的工作空間進行了分析。分析挖掘機的工作空間范圍對于挖掘機作業任務設置和路徑規劃非常重要。鏟斗尖端的實際運動空間是用蒙特卡洛方法繪制的[8]。動臂，斗桿和鏟斗的三個關節角包含大量隨機樣本。鏟斗尖端的位置和姿勢由正向運動學推導。然后，調用Matlab中的描點函數scatter3(x,y,z)描繪出挖掘機隨機關節變量所對應的空間位姿點的位置集合。所有點位置的集合就是挖掘機工作空間的蒙特卡洛分布圖。如圖2所示為挖掘機的工作空間。根據挖掘機工作區圖，可以方便地在鏟斗可及范圍內選擇目標位置，提高挖掘機機器人的工作效率。通常，當使用蒙特卡洛方法分析挖掘機的工作空間時，給出的隨機點越多，結果越接近真實。但是，由于一般工程實踐中有大量計算，如果將挖掘機的工作空間解決在一定的誤差范圍內，這是可以接受的。

圖2 挖掘機的工作空間圖

2 關節空間軌跡規劃

2.1 三次樣條曲線規劃

樣條曲線是指用一條光滑曲線插值或者逼近一組離散有序數據點，最終形成的具有一定性質的滿足條件的曲線，具有可微性、凸包性質，而且生成的運動軌跡曲線具有速度、加速度連續性。三次樣條曲線的表達式如下：

對三次樣條曲線函數求一階導數和二階導數，可以得到各關節的速度和加速度，如下：

初始點和終止點需滿足的條件：

根據上述公式，將所有控制點的動臂、斗桿和鏟斗轉角值代入軌跡多項式、角速度和角加速度方程，以此得到各個多項式的系數。通過Matlab仿真獲得每個關節的關節角度、角速度和角加速度曲線，如圖3所示。

圖3 動臂、斗桿、鏟斗三次樣條曲線運動仿真軌跡

2.2 五段五次多項式曲線規劃

由于高階多項式及其一階和二階導數具有平滑且連續的特性，路徑點過多的軌跡規劃一般采用多項式進行擬合，多項式的一般表達式為：

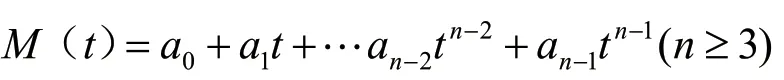
式中：M(t)為隨著時間t變化的關節變量；n為路徑點數。

本研究中n=6，則挖掘機各關節點的多項式為：

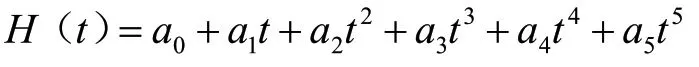
通過對多項式分別求一階、二階導數，得到各關節的速度、加速度公式為：

初始點和終止點需滿足的條件：

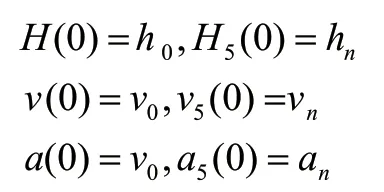
根據上述公式，將所有控制點的動臂、斗桿和鏟斗轉角值代入軌跡多項式、角速度和角加速度方程，以此得到各個多項式的系數。通過Matlab仿真獲得每個關節的關節角度、角速度和角加速度曲線，如圖4所示。

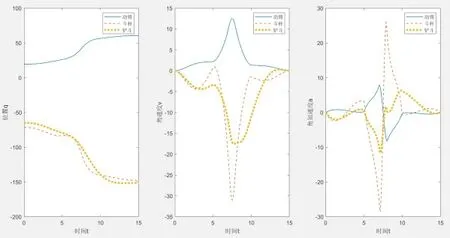
圖4 動臂、斗桿、鏟斗五段五次多項式運動仿真軌跡

3 結論

本研究結合挖掘機實際工作參數，在關節空間對挖掘機工作裝置自主作業過程分別采用三次樣條曲線、五段五次多項式進行軌跡規劃，通過對規劃結果的動力學特性指標進行比較，得出五段五次多項式效果相較于三次樣條曲線更好，五段五次多項式軌跡規劃得到的各個關節的角加速度曲線更為平滑。因此，五段五次多項式規劃挖掘機的運動軌跡，使工作裝置各個關節動作更加平緩且所受的沖擊也更小。三次樣條曲線軌跡規劃的角加速度曲線變化更大，其各個關節所受的沖擊也更大。而在實際作業中，延長各組件的使用壽命是非常重要的一項準則。因此，選用五段五次多項式進行軌跡規劃，能使其受到更小的沖擊，延長挖掘機各組件的使用壽命，也便于挖掘機更好地進行實際作業。