基于ARMA模型的地磁偏角缺數處理方法

董寶偉 錢秋亮 任亞飛,2 陶秋喆,2 邵建龍

1 昆明理工大學信息工程與自動化學院，昆明市景明南路727號，650504 2 云南省麻栗坡民族中學，云南省文山州文麻路193號，663600

地震地磁數據預處理是地磁數據挖掘和地震預報預測的首要工作[1]。地磁觀測數據屬于時間序列，其計算方法要求數據序列連續完整，因此對缺失數據進行插值是前兆數據應用前必須進行的預處理工作[2]。國內外對缺失值進行插值處理的方法較多，如回歸法、最近鄰域替代法、人工填補法和期望值最大化法等[3-5]。武艷強等[6]利用三次樣條插值方法對時間序列中數據缺失較多等問題展開研究；楊登科[7]采用拉格朗日插值等6種方法對時間序列的插值效果進行對比。

在實際地磁偏角觀測工作中，由于地磁觀測數據[8-10]種類眾多，往往會出現單點缺失和連續多點缺失的現象，而現有的數據插值方法在地磁觀測數據的插值應用中存在諸多局限性。目前針對地磁偏角數據插值方法的研究較少，本文根據地磁數據的記錄特點，將時間序列模型[11-12]應用于地磁數據缺失處理。將ARMA預測模型[13-14]用于地磁數據的插值處理，可為地磁觀測數據預處理提供一種可行的方法。

1 插值方法

插值法是數據預處理的重要方法，在數據分析和數據挖掘中發揮著重要作用。常見的插值法有均值插值、線性插值等，不同方法的適用性也不同，如均值插值適用于原始數據方差較小、序列趨于平穩的數據，而本文所采用的地磁觀測數據屬于非平穩數據；線性插值為直線擬合運算，適用于趨勢性較小的數據。但在處理連續多點缺失的數據時，上述方法的插值效果均不理想。本文嘗試將ARMA模型預測方法應用于地磁序列插值。

1.1 均值插值

均值插值就是計算數據的平均值并代替原始數據中的缺失部分，假設求解Ti和Ti+1之間任意一點T，則直接取T為Ti和Ti+1的平均值。對于數據集data=[45.20,26.21,42.10,NaN,NaN,NaN,52.20,32.52]，Python可調用均值mean()函數計算均值，利用自帶fillna()函數進行mean插值計算，計算方法如下：

data = data.fillna(data.mean())

(1)

1.2 線性插值

線性插值是通過已知量來求解兩者之間的未知量，由于其為直線擬合，適合處理較為平緩的數據。在Python中可用interpolate()函數進行線性運算，利用fillna()函數進行interpolate插值，計算方法如下：

data = data.fillna(data.interpolate())

(2)

或

data=data.interpolate(method=‘linear’)

(3)

1.3 自回歸移動平均(ARMA)模型

本文嘗試將ARMA模型作為插值方法引入到地磁觀測數據插值預處理中。將缺失數據作為時間序列預測數據，利用缺失序列之前的數據預測缺失數據，插值效果較好。

ARMA模型作為一種時間序列經典模型，由自回歸模型(AR)和移動平均模型(MA)組合而成，其結構為：

xt=φ0+φ1xt-1+φ2xt-2+…+φpxt-p+

εt-θ1εt-1-θ2εt-2-…-θqεt-q

(4)

式中，隨機變量Xt的取值xt不僅與前p期的序列值有關，還與前q期的隨機擾動有關，p為自回歸模型階數，q為移動平均模型階數。

ARMA(p,q)模型預測步驟如下。

1)非白噪聲檢驗：使用Python自帶函數庫statsmodels中acorr_ljungbox函數進行檢驗，若p值小于顯著性水平α，則該序列為非白噪聲，具備建模分析價值。

2)平穩性檢驗：使用Python自帶函數庫statsmodels中adfuller函數進行檢驗，也可通過地磁序列的自相關函數(ACF)和偏自相關函數(PACF)來確定序列是否平穩，若不平穩可使用差分方法使數據序列達到平穩，進而確定模型階數(p、q值)。

3)估計：對模型參數進行評估。

4)預測：利用擬合模型進行預測分析。

為驗證利用ARMA模型對地磁數據進行插值的可行性和有效性，將常用的均值插值、線性插值的插值結果作為參照，與ARMA模型的插值結果進行對比研究。

2 地磁數據插值實驗設計

2.1 前期地磁數據處理

ARMA模型要求數據序列必須為平穩數據，對于地磁觀測數據而言，數據序列由各種趨勢、周期和隨機干擾組合而成，因此在建立ARMA模型之前需要去除數據中的趨勢和周期成分。通過分析地磁偏角觀測數據模型，可將地磁數據的曲線形態分為三類：1)隨機干擾；2)地球背景場或太陽輻射周期；3)周期或趨勢成分。由于地震儀器所處的臺站和自然環境不同，其記錄的地磁數據均包含不同形態的趨勢和周期成分。

去除趨勢或周期、地球背景場或太陽輻射周期最簡單的方法是對地磁觀測序列進行差分處理。對于多數觀測序列而言，一階差分即可去除大部分干擾成分，使數據序列達到平穩，若一階差分數據仍未達到平穩，可進行多次差分。對大量觀測數據序列進行統計分析發現，約92.43%的地磁觀測數據序列為非平穩狀態，經過一階差分后，96.78%的非平穩序列均可達到平穩[1]。在對地磁偏角進行處理時發現，為了使觀測數據趨于平穩化，對觀測數據進行二階差分，非平穩數據基本可達到平穩化。

2.2 地磁插值實驗方法設計

2.2.1 非震異常數據數量≤10

為比較ARMA模型與其他插值方法的插值效果，選取完整的地磁觀測數據序列，人為構造缺失數據。數據缺失點包括單點缺失和連續多點缺失，本文設計的連續多點缺失為2～10點缺失，利用3種不同的插值方法對缺失數據序列進行插值處理。選擇缺失值之前的400個數據點作為ARMA模型的基礎，并確定參數最佳的ARMA模型，然后將預測值作為缺數填補結果。采用標準誤差作為評價指標，標準誤差越小，插值效果越優。標準誤差計算公式如下：

(5)

式中，n為缺值個數，xi為插值結果，yi為實際觀測值。

2.2.2 插值實驗及分析

選取地磁偏角D數據，對地磁數據各種缺失情況進行插值實驗，步驟如下：

1)在地磁偏角數據中選取10個位置點作為缺失數據的起始點。

2)依據起始點連續構造n(n取值1～10，分別對應10種缺失情況)對缺失數據序列進行差分處理。

3)采用3種不同方法進行插值處理。

4)利用式(5)計算3種不同方法的標準誤差。

表1為實驗結果，從表中可以看出，3種插值方法中ARMA預測插值法的插值效果較好，其次為線性插值法和均值插值法。圖1為3種插值方法的平均標準誤差曲線，從圖中可以看出，在不同缺失值情況下，3種方法的標準誤差曲線趨勢表明，隨著缺失值個數的增加，插值結果與實際值的標準誤差也在增加，且不同插值方法標準誤差的增長速度有所不同，相比于線性插值和ARMA預測插值，均值插值標準誤差的增長速度最快；ARMA預測插值的效果最好，其標準誤差最小，標準誤差曲線的變化幅度小于其他方法。

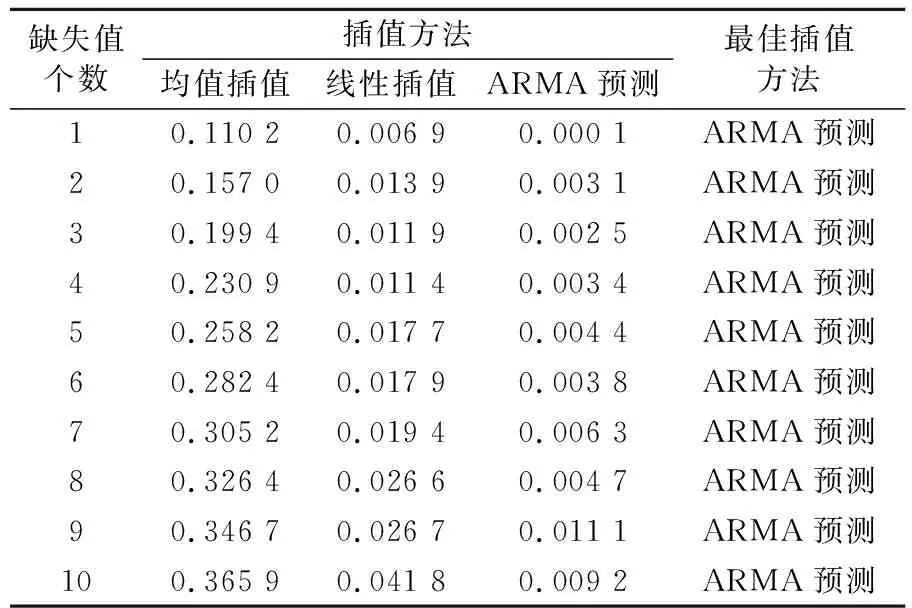
表1 三種不同插值方法在不同缺失條件下的平均標準誤差

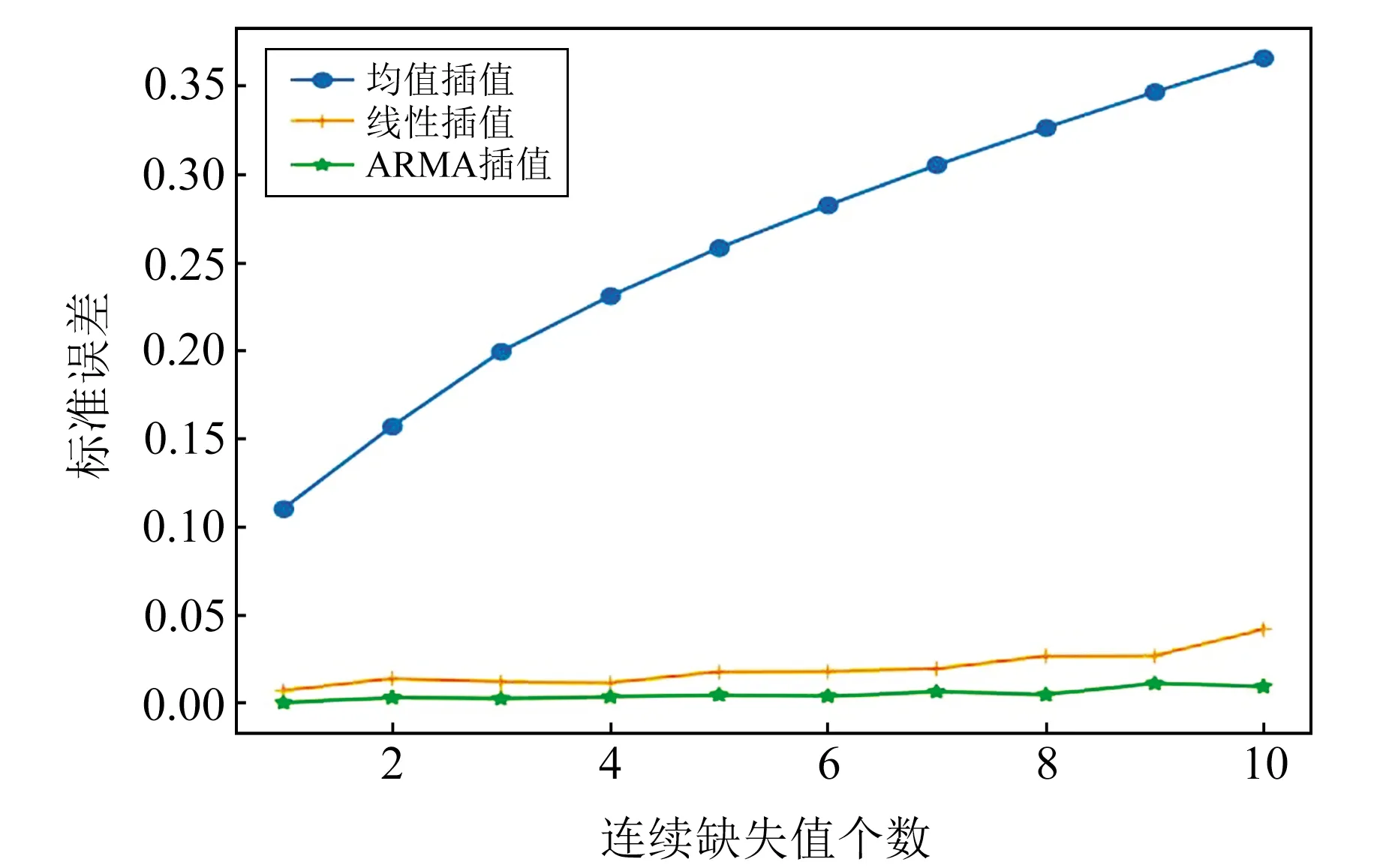
圖1 不同缺失值個數情況下不同插值方法的平均標準誤差比較

圖2為不同單點缺失位置3種插值方法對應的標準誤差變化曲線，從圖中可以看出，ARMA預測插值相比于其他2種方法的標準誤差更小。

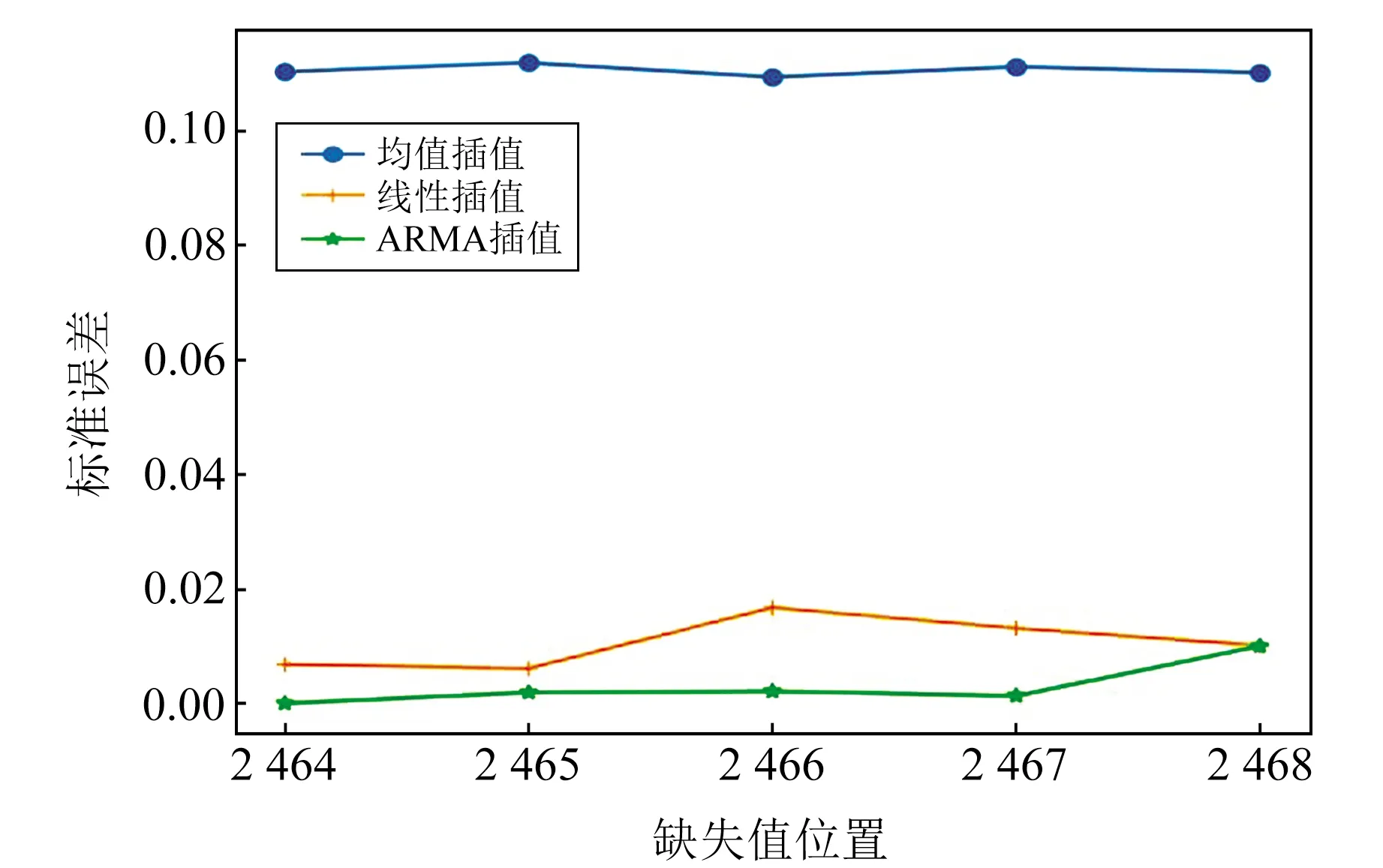
圖2 不同單點缺失位置3種方法對應的平均標準誤差變化曲線

為了能夠更加直觀地說明3種插值方法插值效果的差異，本文以2008-05-12汶川地震北京臺的秒采樣數據為例，給出磁偏角D在連續缺失10個數值時3種插值方法的插值效果(圖3)。

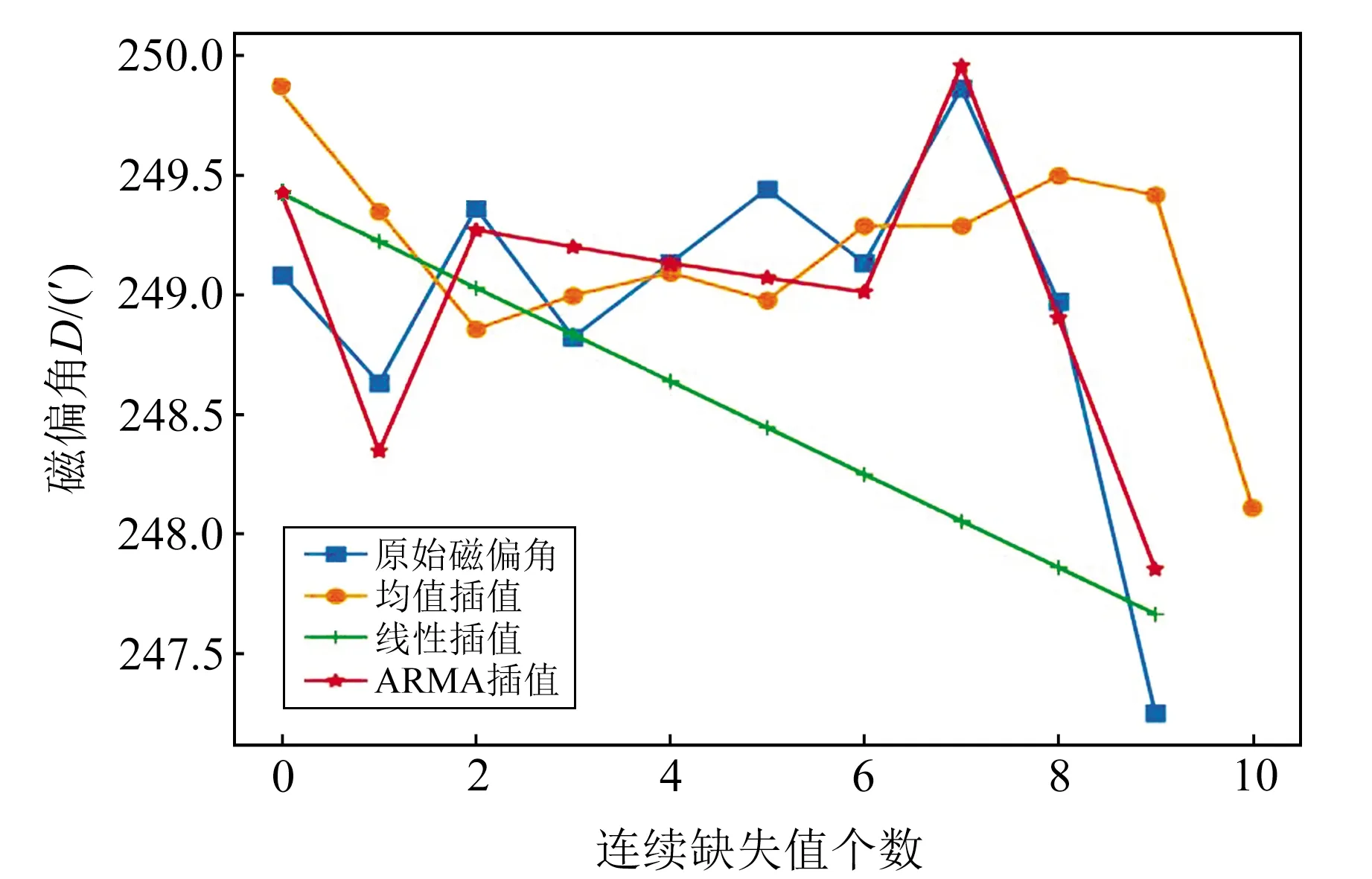
圖3 連續缺失10個數值的插值情況

實驗表明，在均值插值、線性插值和ARMA預測插值中，ARMA模型的插值效果最優。本文以2017-08-08九寨溝地震滿洲里地震臺連續缺失10個數值的地磁偏角秒數據為例進行數據擬合，結果如圖4所示。

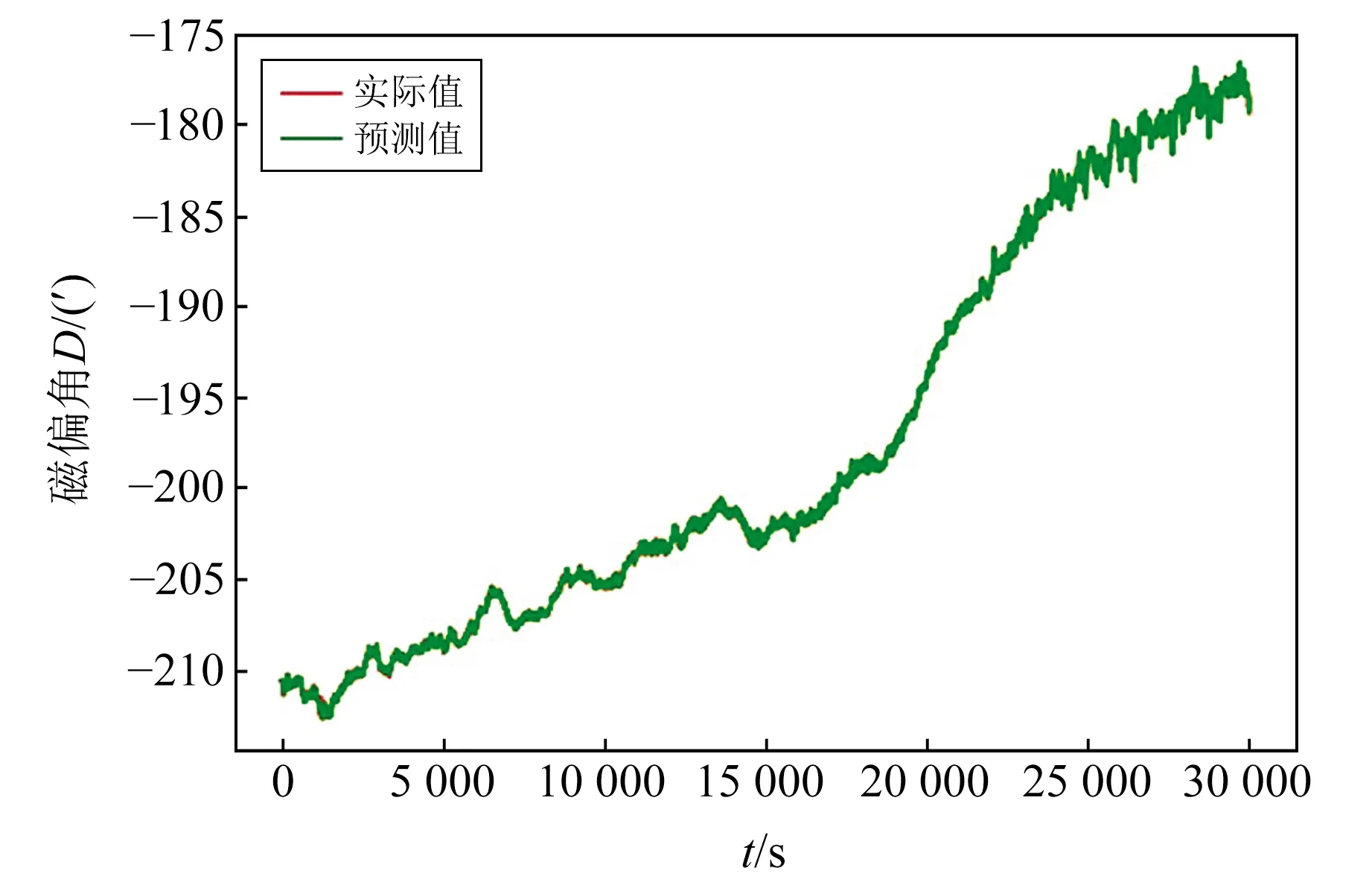
圖4 九寨溝地震滿洲里地震臺連續缺失10個數值的地磁偏角秒數據ARMA模型擬合

綜上分析可知，不同插值方法對不同缺失情況的插值效果各不相同，表現為曲線形態特征存在差異。ARMA預測插值法的標準誤差較小，且該模型中插值數據與實際觀測值擬合度高，而均值插值和線性插值會改變數據原始趨勢，因此ARMA插值對地磁偏角D數據的處理效果相對較好。

2.2.3 非震異常數據數量>10

在數據缺失較多時不應采用插值方法，而應直接刪除。但本文研究的地磁數據屬于時間序列數據，為了后期可檢測到數據異常點，本文采用統一合理值來代替大量缺失數據和非震異常數據。非震異常數據指地震儀器記錄錯誤或未記錄到的數據，其一般為多個連續數值88 888.0或99 999.0，或者為多個連續的小于 99 999.0且遠大于正常地磁峰值的數值。由于地磁由多個變化緩慢的磁場組成，其數值為隨時間變化的時間序列，不可能出現多個連續相同且遠大于正常峰值的數值。因此，該部分數值與真實值無相關性，會對地磁的趨勢信息造成不可恢復的影響。但這部分數據是時間序列的一部分，而時間序列中每個數值所在的時間點也是重要信息，因此應用合理的數值代替該部分數據，有利于保持時間序列的完整性。處理這些數據的算法如下：

1)遍歷1 d內所有的地磁偏角D數據，統計數值為88 888.0、99 999.0及其以上數值的個數，若個數小于10，采用§2.2.1算法進行插值；若個數大于10，則采用鄰域值進行代替，直到出現正常值。

2)遍歷1 d內所有的地磁偏角D數據，若數值出現0或“NaN”的個數小于10，采用§2.2.1算法進行插值；若個數大于10，則采用鄰域值進行代替，直到出現正常值。

3)遍歷1 d內所有的地磁偏角D數據，若重復數值出現的個數小于10，采用§2.2.1算法進行插值；若個數大于10，則采用鄰域值進行代替，直到出現正常值。

以2008-05-12汶川地震滿洲里臺站作為測試臺站，其缺數中88 888.0、99 999.0、0和”NaN”個數大于10，數據為地磁偏角D的1 d秒采樣數據，結果如圖5所示。

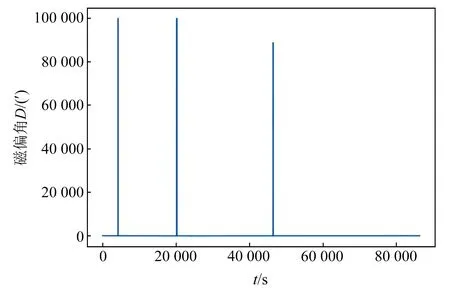
圖5 汶川地震滿洲里臺站多種缺數大于10

由于包含遠大于正常值的數值88 888.0和99 999.0，從圖5中無法看出數據走勢，該部分數據對于后期數據異常分析并不重要，但對異常時間點分析必不可少，因此本文采用鄰域值代替該部分數據(圖6)。鄰域代替屬于就近代替，其數值差距較小，因此處理后的數據和原始數據相差較小。該處理過程是為了保證地磁序列的時序連貫性，并不會對后續分析產生影響。

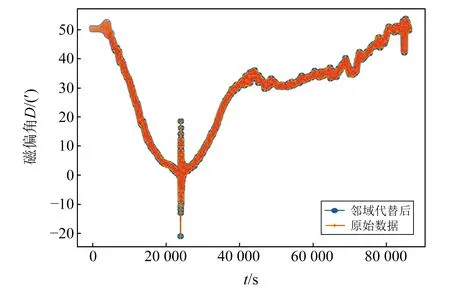
圖6 鄰域值代替缺失數據擬合圖

3 結 語

為了處理地震儀器記錄的非震異常數據，本文將ARMA模型用于數據插值處理，并與均值插值、線性插值的實驗效果進行對比分析，得到以下結論：

1)無論是單點插值還是連續多點插值(2～10個)，ARMA模型的插值效果均優于均值插值和線性插值。

2)ARMA模型能夠較好地保持實際觀測序列的曲線形態，而均值插值和線性插值會改變其形態。

3)均值插值適用于方差小、穩定性好的數據；線性插值適用于曲線形態較為平坦的序列；ARMA模型適用于規律性變化、干擾較小的序列。

4)ARMA模型屬于外插值法，采用該模型進行預測時需要建模，因此與均值插值和線性插值相比耗時較多。由于存在較多的歷史數據作為參考，即使在多點缺失情況下，ARMA的預測效果仍高于其他兩種方法。

5)ARMA模型有望在電磁學領域數據預處理中發揮作用。