基于自適應抗擾控制策略的太陽電池 MPPT的研究

張 兵，楊子林*，郭亞男

(1.南陽農業職業學院機電工程學院，南陽 473000；2. 鄭州經貿學院 智慧制造學院，鄭州 450000)

0 引言

在一定的太陽輻照度和環境溫度下，太陽電池可直接將太陽能轉換成電能[1]，這種發電形式稱為光伏發電。太陽電池在某一輸出電壓值時，其輸出功率能達到最大值，光電轉換效率達到最高，此時太陽電池中輸出功率-電壓曲線的工作點達到最高，此點被稱為最大功率點[2]。根據太陽電池等效電路原理圖，通過設計智能控制器來預測太陽電池可能達到的最大功率點輸出，改變當前電路中的阻抗值，調整太陽電池輸出功率-電壓曲線的工作點，從而保持太陽電池一直運行在最大功率點附近，此工作過程被定義為最大功率點跟蹤(maximum power point tracking，MPPT)[3]。

為提高光伏發電系統的發電效率，需使太陽電池的工作點保持在最大功率點附近。基于此，本文提出了一種基于自適應抗擾控制策略的太陽電池MPPT。根據太陽電池的特性在MATLAB/Simulink中建立太陽電池的仿真模型，對不同環境下的太陽電池輸出特性進行建模和仿真，采用擴張狀態觀測器(ESO)觀測太陽電池的電壓和功率，預測其當前工作點與最大功率點的位置關系，自適應抗擾控制器會根據太陽電池的變化實時調整其工作點，從而實現對擾動的主動抑制，使太陽電池的工作點保持在最大功率點附近。

1 太陽電池仿真模型的建立與特性分析

1.1 光伏發電系統的原理結構

光伏發電的工作原理是利用光生伏特效應將太陽的輻射能量直接轉換為電能。光伏發電系統通常分為獨立式光伏發電系統、并網式光伏發電系統和混合發電系統。其中，獨立式光伏發電系統主要由光伏陣列、控制器、蓄電池組和逆變器構成。獨立式光伏發電系統的基本組成如圖1所示。

圖1 獨立式光伏發電系統的基本組成Fig. 1 Basic composition of independent PV power generation system

1.2 太陽電池仿真模型的建立

太陽電池的等效電路圖如圖2所示。圖中：V為太陽電池的輸出電壓，V；I為太陽電池的輸出電流，A；IL為太陽電池的光生電流，A；Id為二極管的導通電流，A；Rsh為太陽電池的等效電阻，Ω；Ish為太陽電池的等效電流，A；Rs為太陽電池的串聯電阻，Ω。

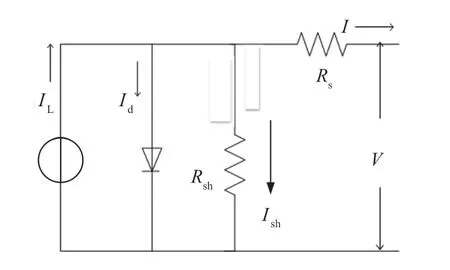
圖2 太陽電池的等效電路圖Fig. 2 Equivalent circuit of solar cell

太陽電池在正常發電狀態下，其電流方程可表示為：

其中，Id可表示為：

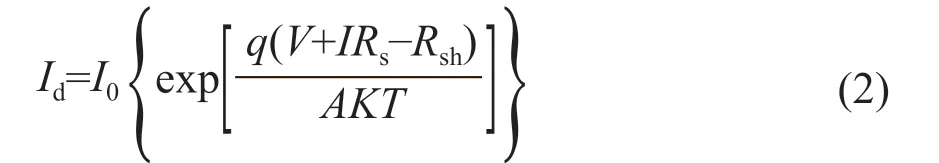
式中：I0為太陽電池的反向飽和電流，A；q為單位電荷量；A為二極管因子；T為太陽電池p-n結的絕對溫度，K；K為普朗克常量。

Ish可表示為：

將式(2)、式(3)代入式(1)，可得到：

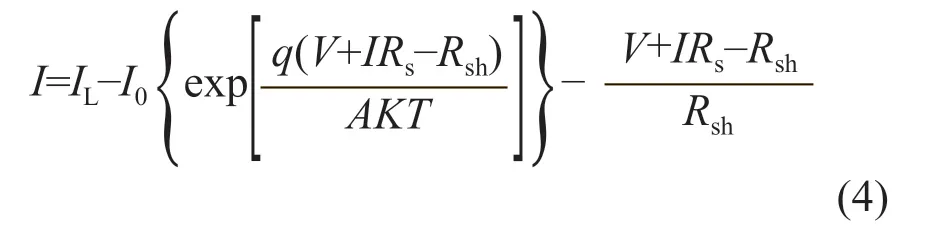
根據太陽電池的物理學原理和數學原理，存在以下情況：

1)由于(V+IRs)/Rsh項的值遠小于光生電流，因此本項可省略；

2)太陽電池正常運行時，Rs值遠小于正向導通電阻，因此設定V=Voc，太陽電池最大功率點處的電壓Vm=V、電流Im=I。其中，Voc為太陽電池的開路電壓，V。

根據上述情況對式(4)進行整理，可得：

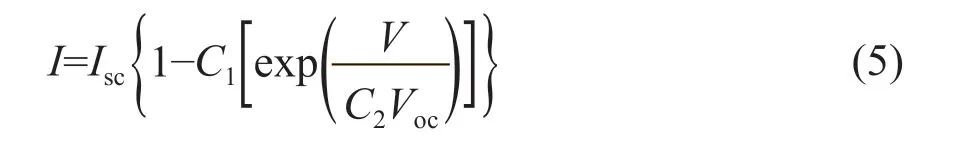
式中：C1、C2均為溫度系數常數；Isc為太陽電池的短路電流，A。

則此時Im可表示為：

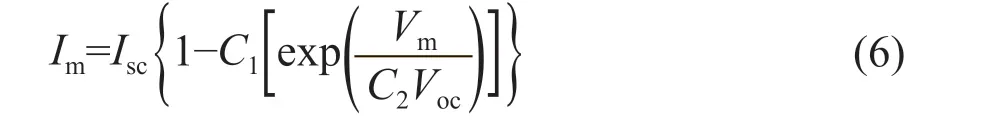
在開路狀態下，當I=0時，V=Voc，因此式(5)可以表達為：

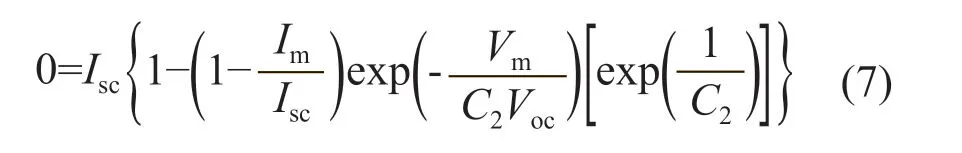
從式(7)可以看出，太陽電池的I-V特性曲線與太陽輻照度和太陽電池的工作溫度有關。地面上太陽輻照度S的變化范圍為0～1000 W/m2，太陽電池的工作溫度的變化范圍為0～60 ℃[4]。

任意太陽輻照度S、環境溫度Tair與太陽電池p-n結的絕對溫度T三者之間存在如下關系：

式中：J為常量，℃·m2/W，本文取0.0289。通過對標準測試條件的太陽輻照度和標準測試條件的太陽電池工作溫度下太陽電池I-V特性曲線上任意點(V，I)的移動，可得到新的太陽輻照度和新的太陽電池工作溫度下太陽電池I-V特性曲線上任意點(V′，I′ )的表達式，即[5]：

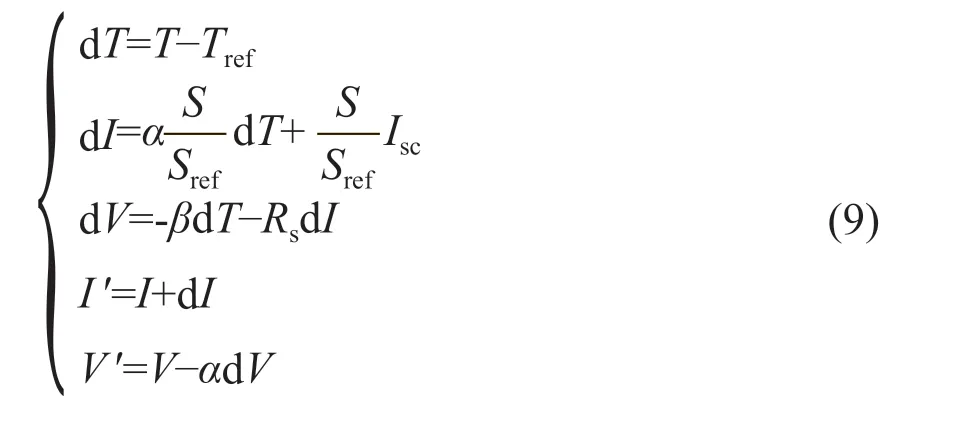
式中：α為標準測試條件的太陽輻照度下太陽電池的電流溫度系數，%/℃，根據太陽電池實測值，α=0.00267Isc；β為標準測試條件的太陽輻照度下太陽電池的電壓溫度系數，%/℃，根據太陽電池實測值，β=0.0671Voc；Tref為標準測試條件下的環境溫度，℃；Sref為標準測試條件下太陽電池的工作溫度，℃。

針對太陽電池的工作過程和輸出特性，考慮太陽電池光電轉換效率影響因素，建立太陽電池的數學模型。根據數學模型進行MATLAB/Simulink仿真，建立太陽電池仿真模型，從而獲得太陽電池在不同環境及環境變化時的I-V、P-V輸出特性曲線，數學模型和仿真結果可以反映出太陽電池各項參數的變化規律。太陽電池的仿真模型如圖3所示。

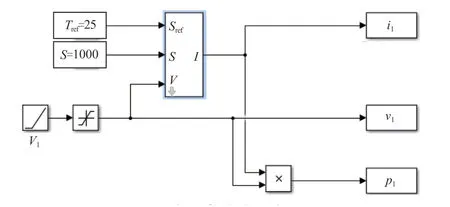
圖3 太陽電池的仿真模型Fig. 3 Simulation model of solar cell

1.3 太陽電池的輸出特性分析

建立太陽電池仿真模型后，觀察并分析太陽電池的輸出特性。

將太陽電池仿真模型中的太陽輻照度S設置為1000 W/m2，對太陽電池工作溫度Sref分別為25、35、45 ℃時太陽電池的P-V輸出特性進行仿真模擬，得到的結果如圖4所示。

通過圖4中太陽電池的P-V輸出特性曲線可知，在太陽電池未達到最大功率點時，其P-V輸出特性曲線近似一條有斜率的直線，輸出功率隨電壓的升高而升高；而當太陽電池達到最大功率點之后，隨著電壓的升高，其輸出功率迅速下降。

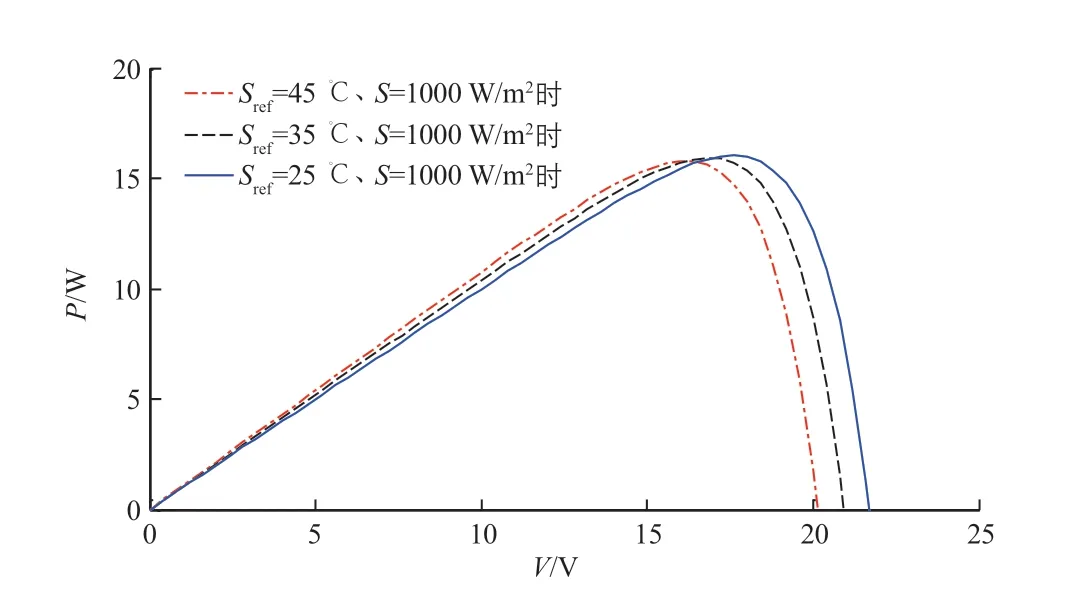
圖4 太陽輻照度為1000 W/m2，工作溫度分別為25、35、45 ℃時太陽電池的P-V輸出特性曲線Fig. 4 P-V output characteristic curves of solar cell when solar irradiance intensity is 1000 W/m2 and working temperature is 25, 35 and 45 ℃ respectively

2 自適應抗擾控制器設計

在本文的MPPT控制算法分析中，MPPT控制的本質就是改變占空比D，進而改變脈沖寬度調制(PWM)波形，利用Boost電路實現阻抗匹配，最終得到太陽電池的最大輸出功率[6]。因此，控制D的取值是本文研究的關鍵和重要依據。基于此，本文設計了一種自適應抗擾控制策略，采用自適應抗擾控制器。

自適應抗擾控制器的設計思路是在模型參考自適應控制器(MRAC)與自抗擾控制器(ADRC)的設計基礎上，融合這2種控制器各自的優點而得到的。在自適應抗擾控制器的整體結構中，采用ESO觀測太陽電池的電流、電壓、功率等狀態變量，設定電路阻抗匹配值，與參考模型求誤差，根據MRAC的特性設計自適應控制律，消除狀態誤差，使被控制對象的狀態性能與參考模型趨于一致[7]。

自適應控制器模型如圖5所示。圖中：xp為被控對象的狀態量；u為控制輸入量；xm為參考模型的狀態量；r為設定輸入量；e為狀態誤差；F為狀態反饋控制器的狀態反饋；K1為狀態反饋控制器的增益。

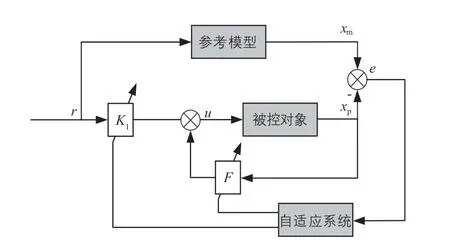
圖5 MRAC模型Fig. 5 MRAC model

考慮被控對象的特性和干擾因素，設計合理的自適應控制律成為保證自適應抗擾控制器控制效果的關鍵。為了保證太陽電池的穩定，本文以李雅普諾夫(Lyapunov)函數作為判別太陽電池穩態的方法，由于該函數具有普遍性和實用性，因此可根據不同階次的狀態方程和Lyapunov函數設計自適應控制律，從而保證太陽電池實現動態響應快、魯棒性強和抗擾能力強的效果。

考慮太陽電池為二階非線性系統，設定其中狀態變量可觀，則太陽電池的空間方程可表示為：

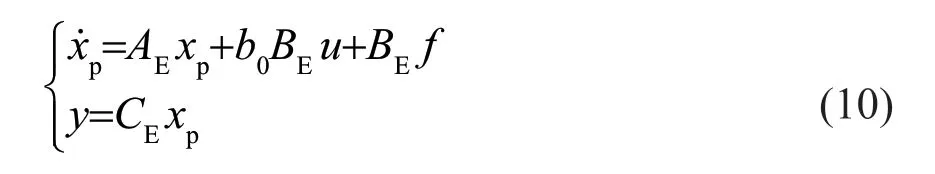
式中：AE、BE、CE均為矩陣；為被控對象的擴張狀態量；b0為外部擾動量；f為控制系統的擾動量；y為輸出量。

給定太陽電池的參考模型的狀態空間方程為：

MRAC的調節過程為：給定信號r并作用于太陽電池和太陽電池參考模型的初始輸入端，則太陽電池的響應輸出中的狀態誤差=可表示為：

MRAC的控制系統根據太陽電池特性設計自適應控制律，實時調整太陽電池的參數，即狀態反饋控制器的F和K1，保證控制系統實際的響應輸出信號與理想的響應輸出信號之間的誤差趨向于零[8]，即：

式中：t為時間，s。

ADRC根據太陽電池仿真模型的不確定性和非線性等擾動因素，將這些影響控制效果的擾動因素作為其控制系統的總擾動，由ESO進行控制系統變量的觀測和補償，使控制系統變為串聯積分結構，最后設計極點配置方式對響應輸出信號完成良好的跟蹤效果[9]。ADRC模型如圖6所示。圖中：d為擾動；Z為ESO的狀態量；n為狀態個數。

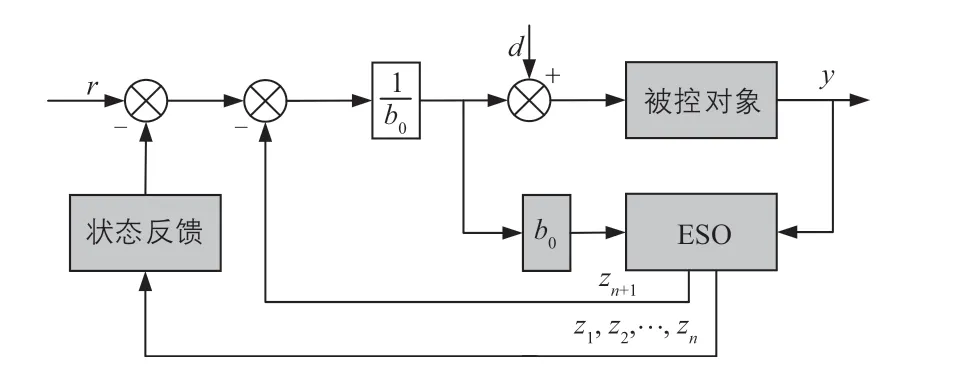
圖6 ADRC模型Fig. 6 ADRC model

太陽電池是一種典型的非線性系統，在工作過程中受到環境溫度、太陽輻射強度的影響，會使模型參數發生改變，因此傳統的控制器難以達到較高的控制精度[10]。MRAC在模型參數不確定的情況下能夠自動調整自適應控制律，使被控對象的輸出趨近于參考模型的響應輸出，具有穩定性好、響應時間快等優點；ADRC能夠實現被控對象擾動的主動抑制，引入ESO完成太陽電池的電流、電壓和功率信號的觀測，使太陽電池的非線性特性具有魯棒性強、抗擾性好等優點[11]。基于以上，自適應抗擾控制器是以ADRC作為內環結構，MRAC作為外環結構，并將2種控制器各自的優點相互結合而設計成的新型控制器。自適應抗擾控制器模型如圖7所示。

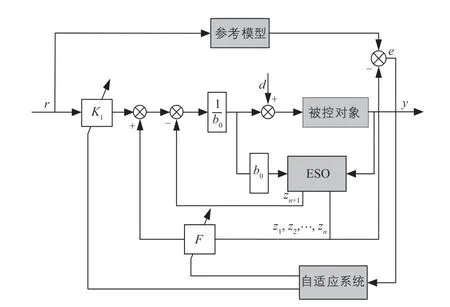
圖7 自適應抗擾控制器模型Fig. 7 Adaptive disturbance rejection controller model

3 MPPT仿真結果分析

在MATLAB/Simulink仿真環境中，針對不同情況的環境變化對4種不同的控制策略進行仿真模擬，并對不同控制策略下太陽電池的輸出功率和占空比D進行比較。4種控制策略分別為：純積分控制、PID控制、自適應抗擾控制、固定步長控制。

將環境溫度設置為25℃，當太陽輻照度在0.10 s中從1000 W/m2降到800 W/m2時，對4種不同控制策略下的MPPT仿真結果進行分析。4種控制策略下的MPPT仿真波形如圖8所示。

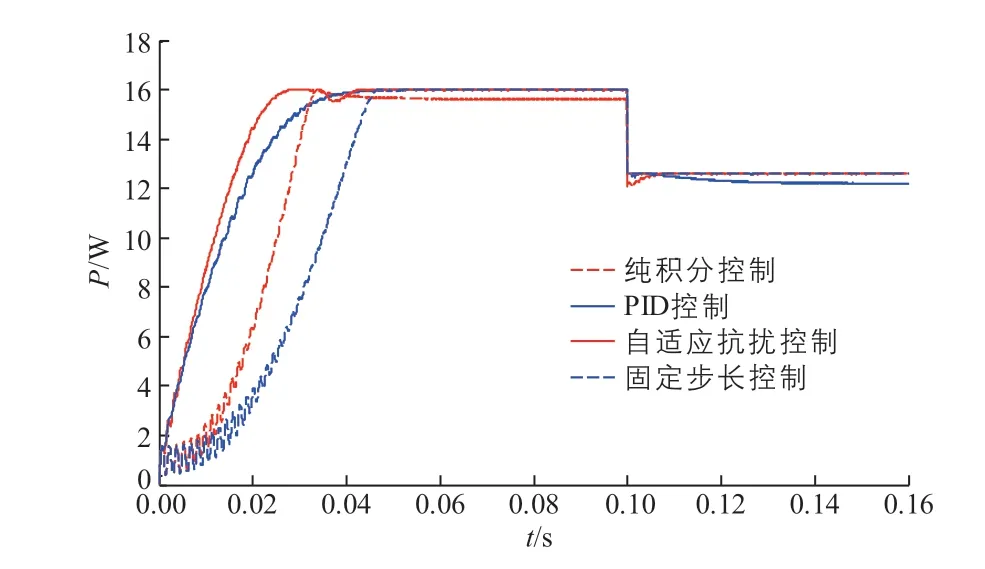
圖8 4種控制策略下的MPPT仿真波形圖Fig. 8 MPPT simulation waveform under four control algorithms

從圖8可以看出，綜合響應時間、超調量和穩定性等方面，4種控制策略下的MPPT仿真波形中，自適應抗擾控制策略針對太陽電池MPPT具有響應時間快、魯棒性強和無靜態誤差等優點，控制效果更好，MPPT控制策略更優。

4 結論

本文為了提高光伏發電系統的發電效率，提出了一種自適應抗擾控制策略，通過對太陽電池的等效電路進行分析并建立太陽電池數學模型，完成了太陽電池的模型仿真，并通過仿真得到了太陽電池的I-V、P-V輸出特性曲線。在考慮了太陽電池的最大功率點影響因素(太陽電池工作溫度和太陽輻照度等)后，根據太陽電池的特性設計了自適應抗擾控制策略，并通過對4種控制策略進行實驗仿真對比，發現本文提出的自適應抗擾控制策略針對太陽電池MPPT具有響應時間快、魯棒性強和無靜態誤差等優點。