磁懸浮冷壓縮機轉子的動力學分析和試驗研究

張舒月，李青，2，伍繼浩?

（1.航天低溫推進劑技術國家重點實驗室，中國科學院理化技術研究所，北京 100190；2.華中科技大學 能源與動力工程學院，湖北 武漢 430074）

隨著超流氦在高能物理、核聚變、超導電力等領域的廣泛應用，大型超流氦低溫制冷系統已成為不可或缺的基礎支撐設施.對于2 K 溫區的大型氦低溫系統，目前國際上普遍通過采用串聯多級離心式冷壓縮機在低溫負壓下對過冷槽減壓降溫的方法來獲得1.8 K～2 K 的超流氦[1].冷壓縮機作為超流氦系統核心部件，需要工作在負壓低溫環境下，工作轉速達數萬轉每分鐘.苛刻的運行條件對轉子的支撐設備提出了較高的要求.常規的油脂潤滑軸承在高轉速下存在摩擦產熱和壽命短等問題；氣體軸承的轉速較高，但由于壓縮機的葉輪端需要工作在2 kPa的低壓環境，采用氣體軸承勢必會對下端低溫軸的密封提出更加嚴格的要求.

主動式磁懸浮軸承（Active Magnetic Bearing，AMB）利用電磁力將轉子無摩擦無潤滑地懸浮于空間，具有無磨損、高轉速、壽命長等普適優點[2].對于立式離心式壓縮機而言，還可以采用主動控制的方式精確定位轉子的軸向位置，改變葉頂間隙，控制進出壓縮機的質量流率，從而達到預防壓縮機喘振的目的[3].主動式磁懸浮軸承被認為是當前超流氦制冷系統中冷壓縮機轉子支撐部件的最佳選擇[4].

根據冷壓縮機的應用需求，建立一套準確和完善的磁懸浮轉子動力學特性的計算方法對于前期磁軸承和轉子的結構設計，以及后期控制參數的實際調試都具有重要意義.轉子的研究歷史較長，目前已有一些商業軟件，如ANSYS、SAMCEF 等.采用有限元方法分析其動力學特性，這也是部分學者研究磁懸浮轉子時常采用的方法[5-7].但這種方法忽略了磁懸浮軸承系統的阻尼作用，并將動態剛度簡化為定剛度，只適合對臨界轉速和不平衡響應的估算.Mushi 等[8]構建了考慮傳感器和功率放大器在內的轉子狀態空間模型，但該模型沒有考慮反饋控制器的作用.王忠博等[9]考慮了包含控制器在內的電控系統作用，但轉子被簡化為僅有一個自由度的剛性質點，難以保證這種動力學特性的計算方法對轉速較高或形狀細長的磁懸浮轉子也同樣適用.G Du[10]等建立了四自由度轉子模型，采用數值計算方法分析系統剛度和阻尼對磁懸浮轉子不平衡振動的影響，但未進行實驗證實.

趙鵬[11]采用傳遞矩陣法構建自由轉子模型，研究了剛度對磁懸浮轉子臨界轉速的影響，但系統的控制作用被等效為固定剛度，且該分析僅限于理論仿真.萬金貴等[12]構建了磁懸浮轉子的完整模型，提出一種臨界轉速理論計算方法，并通過轉子軸心軌跡的發散程度對臨界轉速進行估算，和理論結果進行比較，但是文中所建立的轉子模型基于傳遞矩陣法，模型在表述上不夠直觀，不利于考慮外界激勵，且沒有給出轉子不平衡響應的理論計算方法和對應的實驗驗證.

上述文獻能對磁懸浮轉子的動力學特性進行簡單計算和分析，但由于沒有考慮控制器的作用，或將轉子視為簡單模型等，因此對磁軸承支撐的轉子動力學行為的模擬在一定程度上可能與真實情況存在偏差.Schweitzer 和Maslen 構建了轉子有限元模型，并提出通過采用求解從不平衡干擾到轉子位移的傳遞函數的方式獲得轉子的不平衡響應特性[2].本文沿用傳統轉子頻響特性的求解方法，理解和操作上較為方便，并對控制參數對轉子動力學特性的影響規律進行了詳細探討；最后在磁懸浮冷壓縮機原型實驗臺上對本文提出的動力學分析方法予以實驗驗證，實驗結果和仿真結果較為符合.

1 磁懸浮轉子系統的動力學建模

超流氦制冷系統中某級壓縮機如圖1 所示.壓縮機的額定轉速為50 000 rpm，其轉子由軸向磁懸浮軸承和兩個徑向磁軸承支撐，兩個電感式位移傳感器分布于徑向磁軸承外側，永磁同步電機置于中間位置，用以驅動轉子高速旋轉.

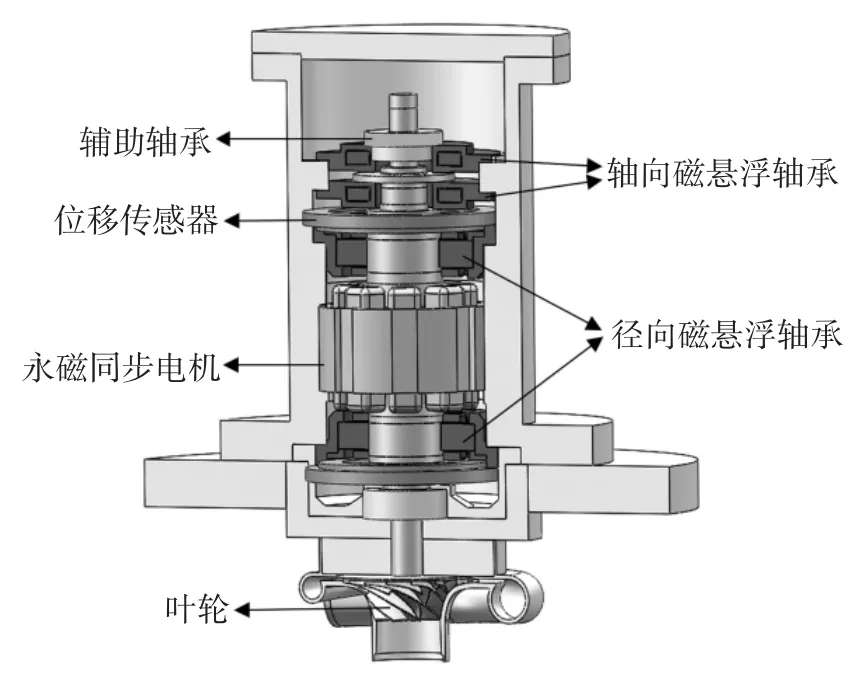
圖1 磁懸浮冷壓縮機剖面結構Fig.1 Sectional structure of magnetic suspension cold compressor

1.1 轉子的有限元模型

磁懸浮轉子重4.85 kg，中間部位的直徑為59.8 mm，實物如圖2 所示.轉子由內部軸芯以及推力盤、徑向磁軸承和傳感器的轉子軸套、葉輪、壓緊螺帽等附件組成.

圖2 磁懸浮冷壓縮機轉子實物Fig.2 Photo of magnetic suspension rotor for cold compressor

在軸的各種模型理論[13]中，鐵木辛柯梁考慮了轉動慣量和剪切變形，適用于分析軸的橫向振動[14]，本文基于該理論基礎為轉子的軸芯建立了彈性梁有限元模型.磁懸浮轉子軸芯所用材料為40 Cr，彈性模量為2.11e11 Pa.永磁電機套筒以過盈的形式裝配在軸芯的中間位置，可以和軸芯看作一個整體.但電機套筒所用材料為釤鈷永磁體，因此在建模時將其彈性模量設定為軸芯材料的一半，為1.08e11 Pa.圖3 是冷壓縮機轉子的有限元模型，其中，中灰色和淺灰色分別代表軸芯和電機套筒.

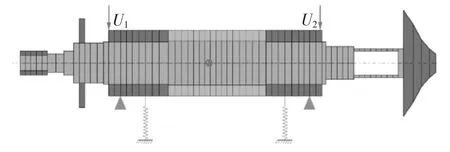
圖3 磁懸浮轉子有限元模型Fig.3 FEM of magnetic suspension rotor

電機套筒兩端主要是傳感器和徑向磁軸承軸套，由0.35 mm 厚的硅鋼片壓制而成，這部分對轉子的橫向彎曲影響較小，因此可忽略剛度，將其視為剛性圓盤單元.壓緊螺帽、葉輪和軸向推力盤也進行了同樣處理.圖3 中的深灰色部分表示剛性圓盤單元.另外，圖中彈簧表示兩徑向磁軸承的位置，三角形表示傳感器位置.為檢測和校正轉子的殘余不平衡質量，轉子軸套兩端沿半徑為25 mm 的周向各設計一圈螺紋孔，見圖中“U1”和“U2”標記處.經測試，轉子在這兩處的殘余不平衡量分別為1.06 g·mm 和0.82 g·mm，相角為171°.

在為轉子進行節點劃分時，磁軸承、傳感器、螺紋孔等關鍵位置均被設置為主節點.為保證計算的快速收斂，在主節點之間劃分數個子節點，使相鄰節點之間的距離盡可能相等.最后得到有64 個節點的轉子有限元模型，其中，徑向磁軸承、位移傳感器和螺紋孔位置分別位于節點21 和43，17 和47，以及15 和48.

通過編寫MATLAB 代碼完成上述轉子模型的建立，得到包含各軸段單元和質量不平衡力的轉子動力學方程如下所示：

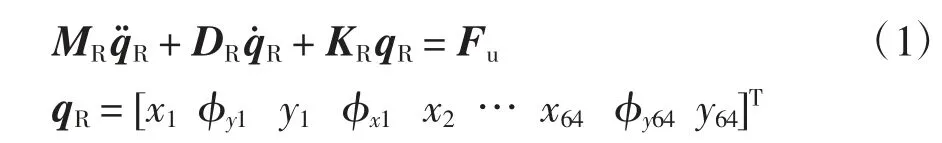
式中：qR為轉子的位移矢量；腳碼數字代表節點數；x和y 分別表示徑向線位移，φx和φy為繞x 和y 的旋轉角位移；質量矩陣MR為剛性圓盤軸段單元質量矩陣Md和彈性軸軸段單元質量矩陣Msn之和，可用下列公式進行求解.

式中：mn和ln分別為第n 段彈性軸單元的質量和長度，mdn和Jdn為第n 段剛性圓盤單元的質量和直徑轉動慣量.阻尼矩陣DR和剛度矩陣KR的求解方法類似，可參考文獻[15].

假設軸套兩端螺紋孔處的殘余不平衡質量分別為me1和me2，偏心距為e1和e2，相位角為φ1和φ2，則這兩處的質量偏心引起的不平衡力fu（t）可寫作如下形式：

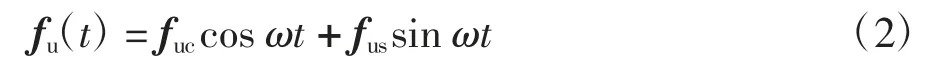
式中：ω 為轉子轉頻，fuc和fus可表示為：

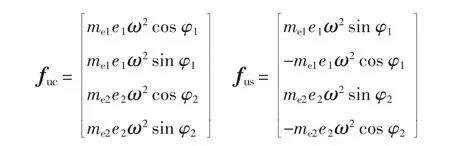
通過引入和螺紋孔所在節點有關的轉換矩陣Tu，將上述不平衡干擾力fu擴展為整個轉子上的廣義不平衡力Fu：

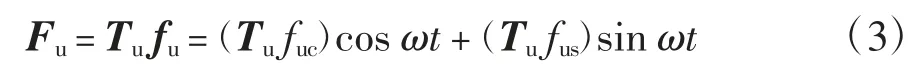
1.2 主動式電磁力

和傳統油潤滑軸承不同，磁懸浮軸承產生的主動電磁力fa取決于繞組線圈的控制電流i 和轉子偏離中心的位移x[2]：

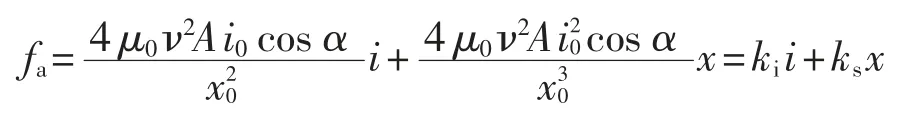
式中：μ0為真空磁導率，A 為磁極面積，ν 為繞組匝數，x0和i0分別為偏置位置和偏置電流，α 為磁極間夾角.ki和ks為電流剛度和位移剛度，僅和磁軸承的結構有關.本文采用的兩個徑向磁軸承的結構相同，實物見圖4 所示；磁軸承的結構參數列于表1.

圖4 徑向磁懸浮軸承定子Fig.4 Stator of radial AMB

表1 磁懸浮軸承的結構參數Tab.1 Structural parameters of AMB

假設磁懸浮轉子在某徑向自由度保持穩定，則：

圖5 是磁懸浮轉子閉環反饋系統，轉子位移x由傳感器傳遞給控制器，經計算后，通過功率放大器轉換為適當范圍內的控制電流i，用以驅動電磁鐵線圈.因此公式（4）中位移x 和電流i 的關系可表示為：

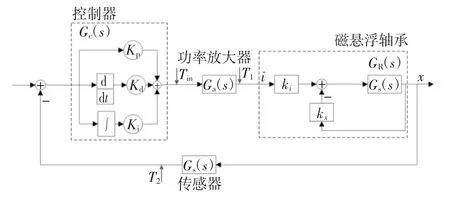
圖5 磁懸浮軸承-轉子系統的閉環反饋框圖Fig.5 Closed-loop feedback block diagram of AMB-rotor system

式中：Ga、Gc和Gs分別為功率放大器、控制器和傳感器的傳遞函數.磁懸浮轉子閉環系統采用三電平功率放大器，經掃頻測試，其增益為0.79，帶寬達2.3 kHz；傳感器增益為20 000 V/m，信號處理電路中抗混疊濾波器的帶寬為3.3 kHz.功放和傳感器的帶寬遠大于額定轉頻，因此可以將傳感器和功率放大器的傳遞函數簡化為常數形式以突出控制器參數與系統剛度、阻尼的關系.

為防止低頻和高頻狀態下，控制器無限放大位移偏差信號，在PID 基本控制器中增加積分時間常數Ti和微分時間常數Td.本文采用的控制器形式如下式（6）所示：

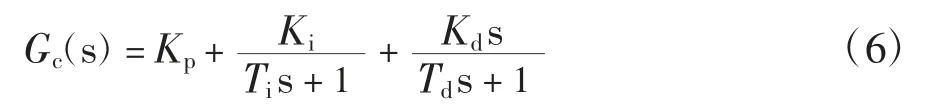
式中：Kp、Ki和Kd分別是比例增益、積分增益和微分增益.

將公式（5）代入公式（4），并進行拉普拉斯變換，整理得：

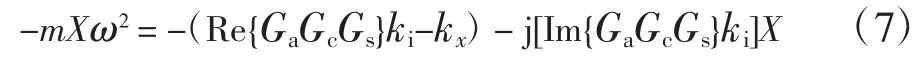
如果用ke表示剛度，de表示阻尼，則質量-彈簧-阻尼系統的動力學方程的拉普拉斯變換形式為：

聯立公式（6）（7），同時對照公式（8），閉環系統的等效剛度和等效阻尼為：

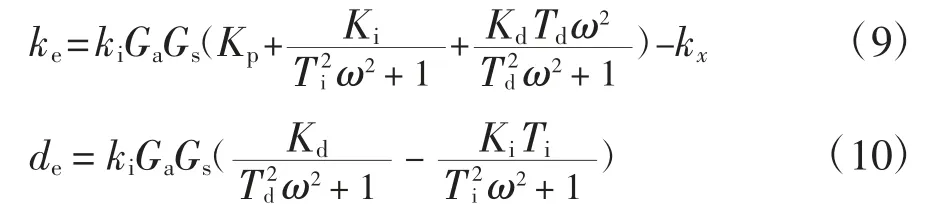
兩徑向磁軸承在x 和y 方向上產生的電磁力可借助剛度和阻尼來表示，qa為兩徑向磁懸浮軸承處的線位移.因此，在整個轉子有限元模型上的廣義電磁力為：

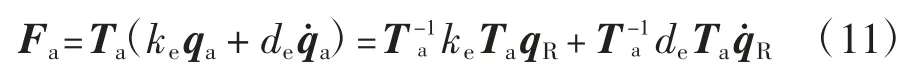
式中：Ta為電磁力的轉換矩陣.

考慮控制器等電控硬件的閉環系統中的磁懸浮轉子的動力學模型可描述為：

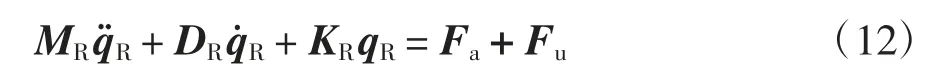
綜合公式（3），整理為如下方程：

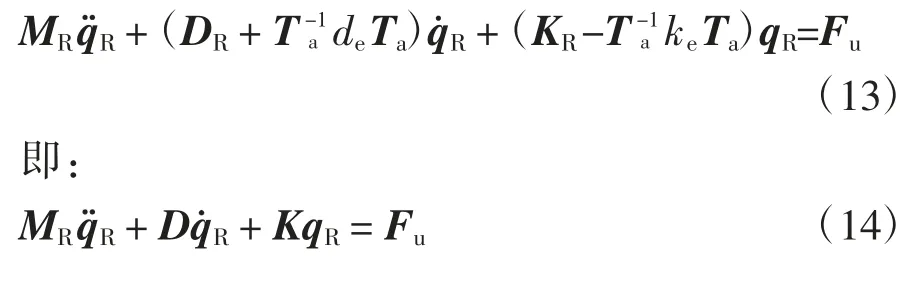
2 磁懸浮轉子的動力學計算

針對公式（14）所示的轉子動力學微分方程組，一般采用模態疊加或者數值分析方法分析轉子的動力學特性.模態疊加法通過解耦處理簡化了原始運動方程，但該方法忽略了系統阻尼的影響[16].數值分析法通過離散時間項得到上述方程的時域近似解，對少自由度模型的求解比較有效，但對高階次有限元轉子模型而言費時費力[10].出于方法的普適性，這里對上述方程進行變換，然后通過求解特征值和特征向量的形式得到臨界頻率和模態振型[15]，通過求解方程的穩態解獲知轉子的振動情況.

2.1 特征值和特征向量

為得到一階微分方程，對上述二階微分方程組進行降階處理.方程（14）轉換為：

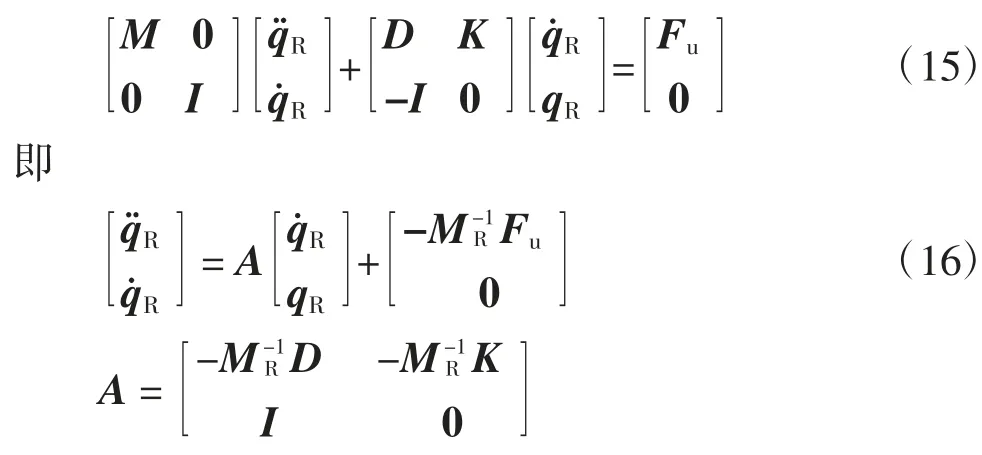
式中：矩陣A 的特征根λ 和特征向量υ 分別對應轉子系統的固有頻率和模態振型.由于轉子模型考慮了陀螺效應，因此特征根可用共軛復數表示：

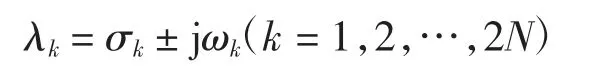
式中：j 為虛數單位，k 為序數，N 表示方程（16）的自由度數，即模型節點數n 的4 倍.特征值的實部σk表示特征阻尼，虛部ωk為固有頻率.

2.2 質量不平衡響應

結合方程（3）和（14），質量不平衡力作為激勵時，轉子的振動方程可表示為：

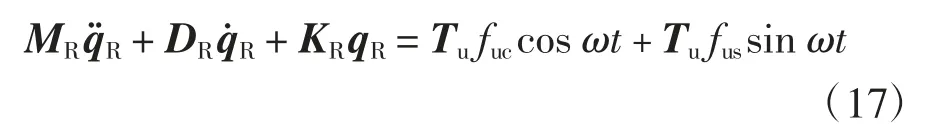
上述方程的穩態解具有這樣的形式[12]：

將公式（18）代入方程（17），整理得：

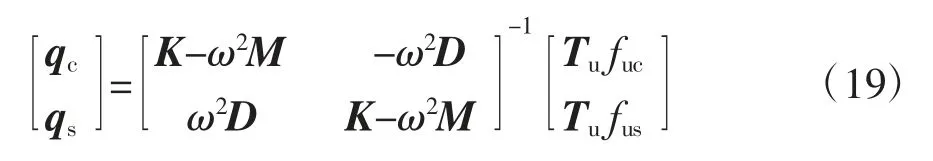
3 磁懸浮轉子動力學特性仿真

磁懸浮轉子的動力學特性不僅取決于轉子和磁軸承結構，還和控制器有關.根據本文提出的建模方法和上述動力學計算公式，本節將解釋PID 參數的選擇依據，并對該控制參數下磁懸浮轉子的臨界轉速和不平衡響應進行仿真計算.

3.1 控制器參數的取值范圍

對于結構已經確定的磁懸浮轉子，可以通過改變控制器參數主動調整系統的剛度和阻尼，以實現磁懸浮轉子的穩定及良好的動態性能.

公式（6）中，微分項的截止頻率和工作頻率有關，本文取800 Hz；積分項的截止頻率較低，取0.75 Hz.容易證明，對于處于0.75～800 Hz 頻率范圍內的磁懸浮轉子，公式（9）中積分增益和微分增益對控制器剛度的影響較小，在初期進行控制器參數整定時可忽略處理，因此：

為穩定轉子，控制系統提供的剛度需大于磁軸承的本身負剛度[2]，即位移剛度.但過大的剛度要求高帶寬的功率放大器，且可能會造成磁場飽和.如果系統剛度取位移剛度的1～3 倍，則由公式（20）得：

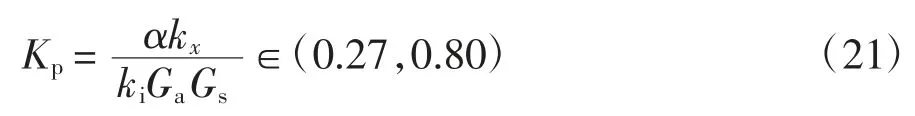
式中：α∈（1，3）.

同理，系統阻尼和微分增益的關系式可簡化為：

為獲得較好的靜、動態響應性能，壓縮機和磁懸浮軸承的相關標準[17，18]要求額定轉速范圍內系統的阻尼比大于20%.然而大阻尼比會導致噪音信號的放大以及造成控制信號飽和.如果將阻尼比的范圍取為20%～70%，聯立阻尼比公式和公式（22），得：

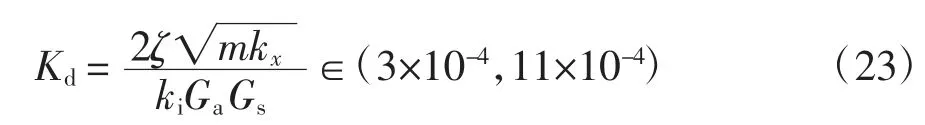
3.2 Kp 和Kd 對轉子動力學特性的影響

公式（21）和（23）所列參數取值范圍能夠保證轉子穩定懸浮.在該范圍內改變Kp和Kd，可進一步研究控制器關鍵參數對磁懸浮轉子動力學特性的影響規律.

冷壓縮機轉子被設計為剛性轉子，因此額定轉速范圍內轉子位移振動達到最大時的頻率可看作剛體臨界轉速.剛體臨界轉速隨Kp和Kd的變化曲線分別如圖6 和圖7 所示.

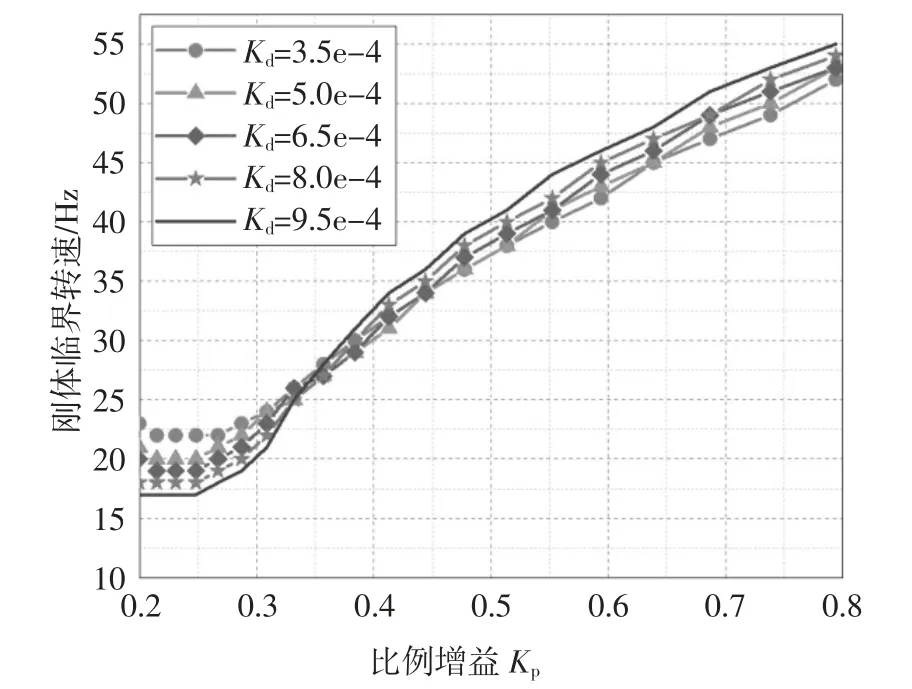
圖6 臨界轉速隨比例增益的變化曲線Fig.6 Critical speed as the function of proportional gain

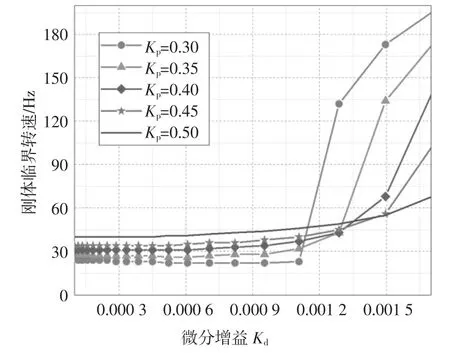
圖7 臨界轉速隨微分增益的變化曲線Fig.7 Critical speed as the function of differential gain

由圖6 可知，在0.27～0.8 范圍內，隨Kp的增加，剛體臨界轉速從約20 Hz 增加到53 Hz 附近，增加的速度逐漸平緩.這表明通過增減Kp可改變剛體臨界轉速，從而有可能避免轉子在升速時的大幅振動，使得整個過程的運行更加平穩.此外，由上圖還可以獲知，隨Kp增加，臨界轉速和Kd由負相關逐漸變為正相關.但整體而言，相比Kp，Kd對臨界轉速影響較小.

由圖7 知，在0.000 2～0.001 1 范圍內，隨Kd的增加，剛體臨界轉速基本保持在30 Hz，超過0.001 1，臨界轉速對Kd異常敏感.這說明當處于合適范圍內，臨界轉速幾乎不受Kd的影響，計算系統剛度時可對控制器的微分作用進行忽略處理；但當Kd較大時，即使微小變化，也會造成臨界轉速的急劇改變，轉子工作于這種狀態是十分危險的.

圖8 和圖9 分別是某傳感器觀測到的位移振動峰值隨Kp和Kd的變化情況.由圖8 可知，隨Kp的增加，轉子的位移振動峰值呈現先增大后減小的趨勢，這一過程的極值隨Kd的增加而減小.圖9 中位移振動峰值的變化趨勢和圖8 類似，即隨Kd的增加先增大后減小，但這一極值隨Kd的增加而增大.這表明在極小的Kd作用下，Kp的增加反而可能會加劇轉子運轉過程中的位移振動.

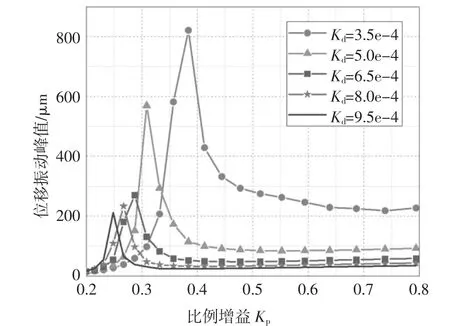
圖8 位移振動峰值隨比例增益的變化曲線Fig.8 Displacement vibration peak as the function of proportional gain

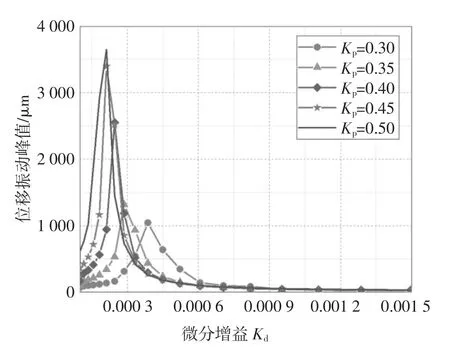
圖9 位移振動峰值隨微分增益的變化曲線Fig.9 Displacement vibration peak as the function of differential gain

磁懸浮轉子輔助軸承的氣隙為150 μm，綜合考慮轉子的位移振動情況，一組合適的Kp和Kd可選擇為0.35 和0.000 60.控制器的積分項用于消除轉子的靜態誤差，本文選取為Kp的10 倍，即Ki=3.5作為控制器的積分增益.為方便對比，接下來的仿真計算和實驗測試均采用上述控制器參數值.

3.3 臨界轉速

通過求解公式（16）中特征矩陣A 的特征值λk可獲知轉子的特征頻率信息.計算不同轉速下的特征頻率ωk，連接同一模態下的特征頻率，連線和轉速的交點為轉子的臨界轉速，如圖10 所示，即上述PID 控制參數作用下的坎貝爾圖.

由圖10 知，磁懸浮轉子的彎曲渦動頻率隨轉速線性變化.但和自由轉子不同的是，剛體臨界轉速在低轉速下呈現非線性變化.這是由于在控制器作用下，閉環系統中轉子的剛度并非固定值，而是隨著轉速發生變化（見公式（9）），且在轉速小于約2 000 rpm 時，這種變化比較明顯.

⑤爆破堆石區。該區位于過渡料區下游，形成下游上壩道路和下游壩坡，是壩體的主要支撐結構，為石料場及建筑物開挖爆破料，碾壓層厚0.8 m，孔隙率小于或等于21%。

在實際運轉過程中，磁懸浮轉子只有前向渦動模態被激發[19].由圖10 知，轉子的前兩階前向剛體臨界轉速分別在25 和40 Hz 附近.前兩階前向彎曲臨界轉速分別為2 502 Hz 和4 821 Hz，如果不考慮陀螺效應，前兩階彎曲臨界轉速分別為2 238 Hz 和4 280 Hz.冷壓縮機的最大額定轉速為833 Hz，距離第一階彎曲臨界轉速有較大安全裕度，遠滿足標準要求.

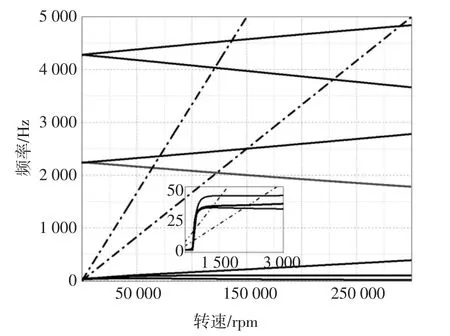
圖10 PID 控制下轉子的坎貝爾圖Fig.10 Campbell diagram of the rotor with PID controller

3.4 不平衡響應

根據公式（19）求得兩傳感器處轉子的位移振動情況，如圖11 所示.在上述PID 控制器參數下，轉子在27 Hz 附近振動較大，上下傳感器觀測到的位移振動峰值分別為89 μm 和55 μm，越過振動峰值，轉子運行較為平穩.與圖10 所示坎貝爾圖中的兩個剛體模態不同，不平衡響應仿真只觀測到一個振動峰值，這是由于平動模態頻率和錐動模態頻率過于接近.

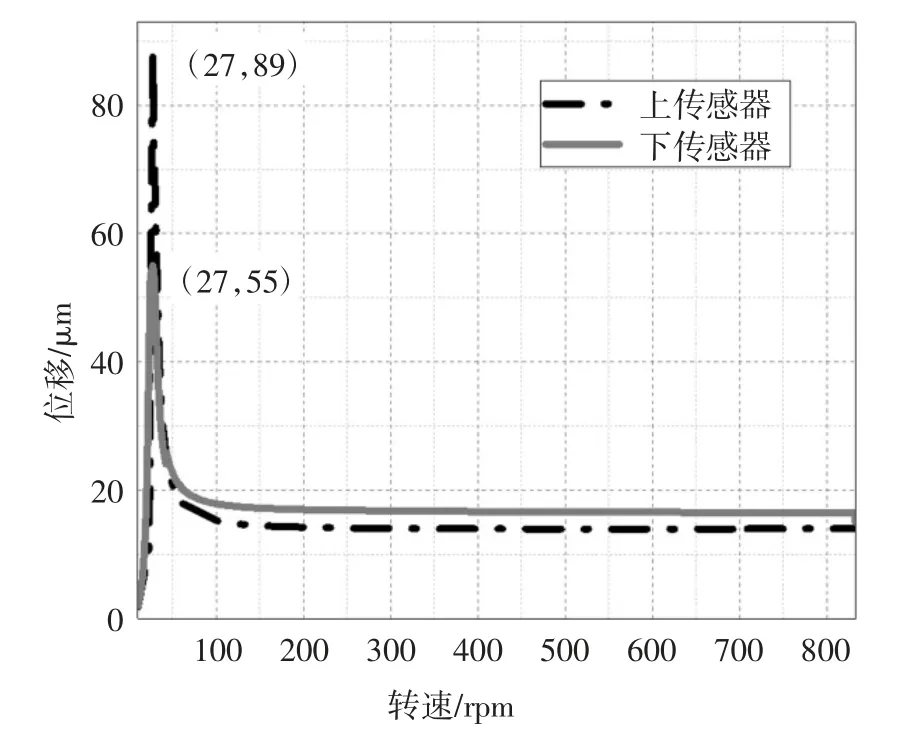
圖11 轉子在上下傳感器處的不平衡位移響應仿真Fig.11 Simulation of unbalanced displacement response of the rotor at the upper and lower sensors

4 實 驗

4.1 模態試驗

4.1.1 閉環系統的辨識

為驗證本文所建立的磁懸浮轉子系統數學模型的準確性，采用安捷倫的動態信號分析儀35670A 對閉環系統進行正弦掃頻測試.正弦信號從功率放大器的前端（圖5 中標識為Tin處）輸入，并對從被控對象輸入端（T1）到轉子位移輸出端（T2）的信號進行分析，得到閉環系統中磁懸浮轉子模型第一通道的波特圖，如圖12 黑色虛線所示.

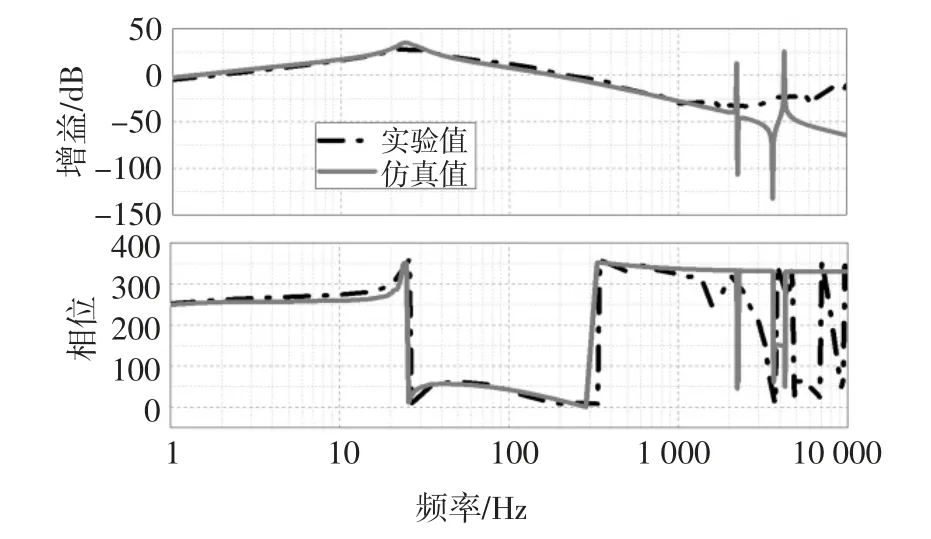
圖12 閉環系統中磁懸浮轉子模型Fig.12 Model of magnetic suspension rotor in closed loop system

圖中灰色實線表示通過仿真計算，得到的對應輸入端到對應輸出端的傳遞函數波特圖.由圖可知，在0～2 000 Hz 范圍內，經仿真計算和模態辨識實驗得到的模型較為匹配，兩種方法獲得的剛體臨界轉速分別為27 和28 Hz.但當頻率較大時難以通過這種方法辨識出磁懸浮轉子模型及其彎曲模態.

4.1.2 力錘激振實驗

磁懸浮轉子的剛體臨界轉速主要受控制器影響，而彎曲臨界轉速主要取決于磁懸浮轉子的機械結構[2]，和控制系統提供的剛度幾乎沒有關系，因此采用錘擊法測量得到的自由轉子的高階臨界轉速可近似看成閉環系統中磁懸浮轉子的臨界轉速.將轉子等分為17 個力錘敲擊點，其中加速度傳感器固定于節點5.為保證力錘激勵帶寬，選取較硬的鋁質錘頭進行錘擊.圖13 中前兩階彎曲臨界轉速分別為2280 Hz 和4 199 Hz，而仿真計算結果為2 238 Hz 和4 280Hz，兩者分別相差1.8%和1.9%.

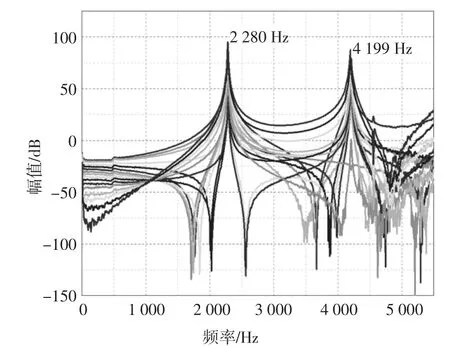
圖13 前兩階臨界彎曲臨界轉速實驗測試結果Fig.13 Experimental results of the first two critical bending mode frequencies

4.2 動力學特性測試實驗

磁懸浮冷壓縮機實驗臺如圖14 所示，它主要由磁懸浮冷壓縮機本體、電控硬件系統、采集和監控系統、控制器開發系統等組成.為測試轉子升速過程中的運行情況，設置轉速的加速度為500 rpm/s，轉子從靜止懸浮勻速緩慢升速到50 000 rpm，傳感器將測得的位移信號傳送至LabVIEW 監控程序.

圖14 磁懸浮冷壓縮機測試實驗臺Fig.14 Test rig for magnetic suspension cold compressor

4.2.2 升速實驗

采用和圖11 相同的PID 控制參數，檢測轉子升速時的位移信號并借助MATLAB 進行分析，得到位移隨轉速變化的曲線圖，如圖15 所示.由圖可知，實際觀測到的轉子的剛體臨界轉速為28 Hz，此時上下傳感器處的位移振動最大，為93/70 μm.和仿真計算的不平衡響應結果（圖11）相比，剛體臨界轉速相差較小，為1 Hz.實驗和仿真結果顯示振動峰值相差4/15 μm，越過臨界轉速，轉子分別穩定在21 μm 和16 μm 附近.

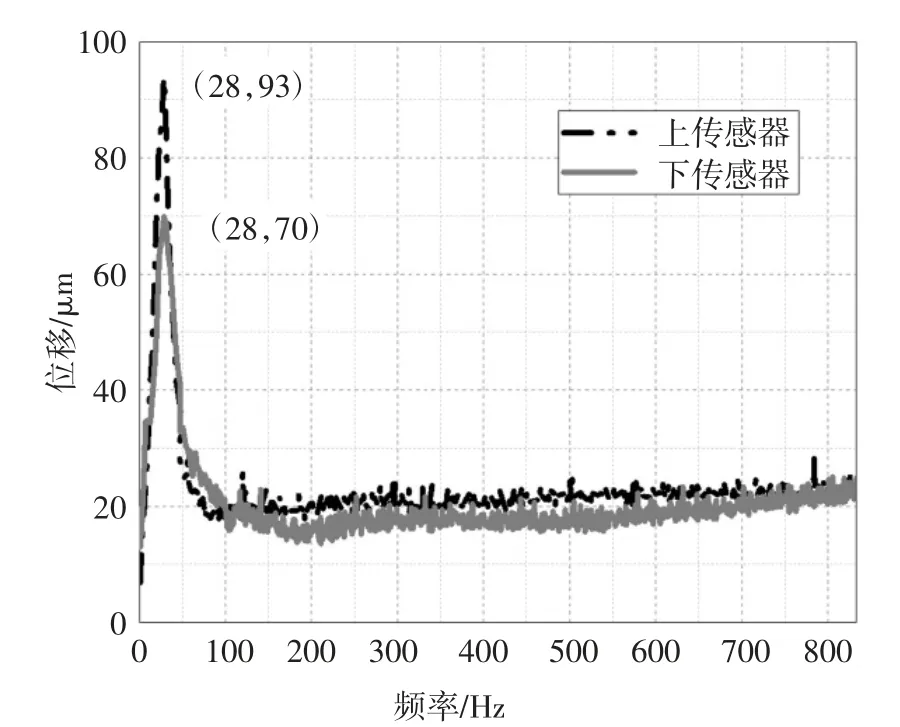
圖15 轉子在升速過程中的位移振動情況Fig.15 Displacement vibration of rotor during speed-up

4.2.3 Kp和Kd對轉子振動的影響

基于前文的仿真結果，當Kp∈（0.35，0.50）且Kd∈（0.000 45，0.000 65）時，轉子振動幅度小于安全氣隙.在該范圍內分別選取五組Kp和五組Kd，并對轉子升速時的振動情況進行測試.

以上傳感器觀測到的位移為例，保持微分增益Kd=0.000 60 不變，Kp分別取0.30，0.35，0.40，0.45，0.50，實驗測得轉子升速時的位移振動情況，如圖16所示.可知，隨Kp的增加，轉子的剛體臨界轉速從25 Hz 逐漸增加到約50 Hz，振動峰值隨Kp的增加從178 μm 逐漸減小到約35 μm.但Kp較大時，如為0.50 時，會造成轉子在高轉速運轉時的大幅振動，這可能是由于系統剛度和阻尼會隨轉速的增加分別增大和減小造成的.

圖17 是保持比例增益Kp=0.35，Kd分別取4.5e-4，5.0e-4，5.5e-4，6.0e-4 和6.5e-4 時，轉子的位移振動情況.可見，轉子的剛體臨界轉速對Kd的變化不敏感，基本維持在30 Hz.但振動峰值隨Kd的增加而明顯降低，從205 μm 降低至約75 μm.由圖16 和圖17 明顯看到，越過剛性模態，轉子運行穩定，位移振動基本不隨Kp和Kd發生改變，保持在21 μm 附近.

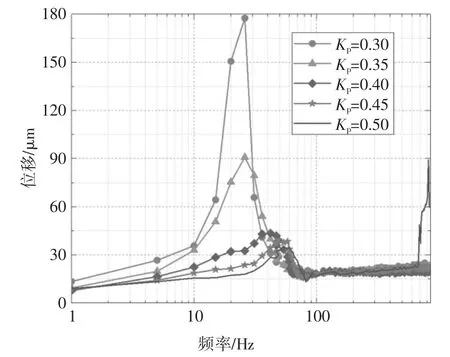
圖16 不同比例增益下轉子的位移振動情況Fig.16 Displacement vibration of the rotor as the function of proportional gains

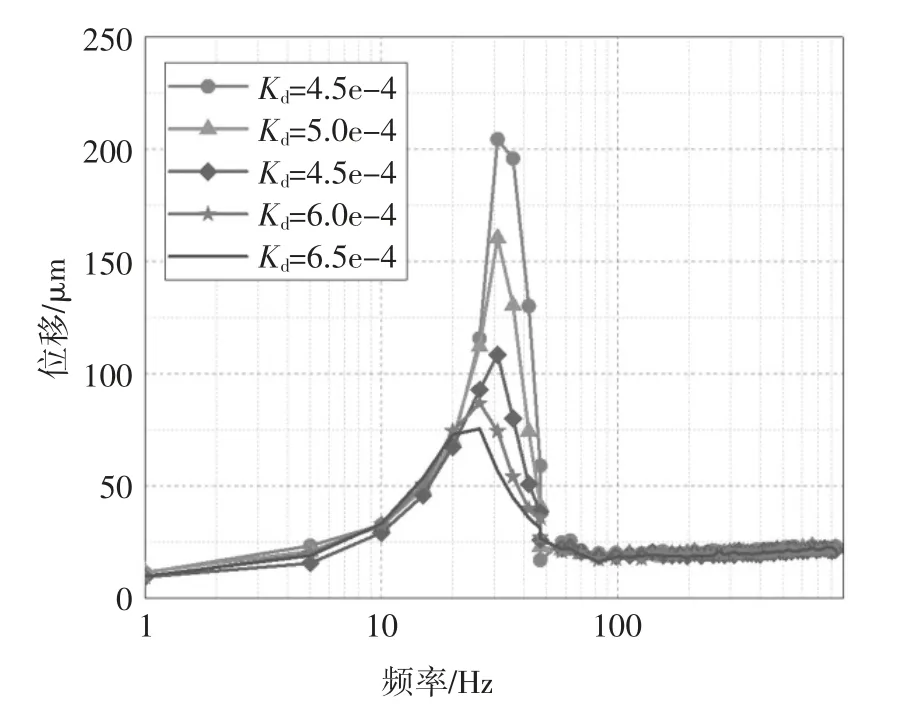
圖17 不同微分增益下轉子的位移振動情況Fig.17 Displacement vibration of the rotor as the function of differential gains

通過圖6-11 以及圖12-17 的對比分析可以發現，仿真計算和實驗測試得到的轉子動力學特性的變化情況較為符合，具體表現為：1）相同控制器參數下轉子的位移振動情況隨轉速的變化趨勢一致；2）當Kd=0.000 60，Kp∈（0.35，0.50），隨著Kp的增加，仿真結果和實驗結果顯示剛體臨界轉速分別從約20 Hz 增加到40 Hz，以及從23 Hz 增加到53 Hz 附近；3）當Kp=0.35，Kd∈（0.000 45，0.000 65），仿真和實驗結果均顯示剛體臨界轉速受Kd的影響較小，基本保持 在 30 Hz 附 近；4）當 Kd=0.000 60，Kp∈（0.35，0.50），隨Kp的增加，仿真結果表明轉子的振動峰值從175 μm 減小到55 μm 附近，實驗顯示從約178 μm 減小到35 μm；5）當Kp=0.35，Kd∈（0.000 45，0.000 65），隨著Kd的增加，仿真結果和實驗結果分別顯示轉子的振動峰值從235 μm 減小到約75 μm，以及從205 μm 減小到約75 μm；6）越過臨界轉速，轉子穩定運行時的振動幅值幾乎不受Kp和Kd的影響，仿真結果顯示轉子穩定在14 μm，而實驗測試的這一數值較大，為21 μm，這可能是由于轉子的不平衡質量的測量值小于其真實值.

5 結論

本文將電控硬件的剛度和阻尼作用加入轉子有限元模型，得到閉環系統中磁懸浮轉子的完整模型及其臨界轉速和不平衡響應的計算方法.基于該方法，研究了控制器關鍵參數對磁懸浮轉子動力學特性的影響特點.通過仿真計算選擇出合適的控制參數，并應用于磁懸浮冷壓縮機實驗臺，對比實驗結果和仿真結果，得到如下結論：

1）通過閉環系統正弦掃頻實驗和力錘激振實驗測得的轉子剛體臨界轉速和彎曲臨界轉速，和仿真結果相比，分別相差1 Hz 和2%.

2）當控制器參數在一定范圍內變化時，仿真和實驗結果顯示：轉子剛體臨界轉速隨比例增益單調增加，但幾乎不受微分增益的影響；轉子升速過程中的振動峰值隨比例增益單調遞減，且隨微分增益單調遞減.

3）相同的控制器參數下，通過仿真計算和升速實驗得到的轉子的剛體臨界轉速和振動峰值較為接近，位移振動隨轉速的變化趨勢一致.

4）實驗和仿真結果的符合性較好說明了本文所提出的磁懸浮轉子的建模方法和動力學分析方法的可靠性.該工作為大型超流氦低溫制冷設備中冷壓縮機的實際調試和應用奠定了重要的理論和實踐基礎.然而，本文的研究對象是第三級壓縮機，且文中實驗是將轉子端部裸露于空氣中，因此葉輪處的周向力可以假設為零.實際各級冷壓縮機在工況、尺寸等方面各有不同，尤其第一級冷壓縮機的入口端為2K 超流氦槽池，易受氣流流動不穩定的影響，此時實際工況下磁懸浮轉子的動力學特性有待進一步深入研究.