砂帶磨削接觸壓強模型分析與實驗*
王亞杰, 黃 云
(1.鄭州航空工業管理學院 航空工程學院, 鄭州 450046)(2.重慶大學 機械與運載工程學院, 重慶 400044)
砂帶磨削去除材料是個十分復雜的過程,磨削壓力是影響材料去除效率的重要因素。在航空發動機葉片的砂帶磨削加工中,把控制磨削壓力作為精準去除材料的主要手段。但是,橡膠接觸輪由金屬材質的輪轂和高彈性材料的橡膠圈組成,橡膠接觸輪與葉片之間的接觸壓強分布不均,從而使接觸區域的材料去除效率不均勻。
為了獲取接觸區域壓強分布的規律,ZHANG等[1-2]將接觸輪與工件之間的接觸近似為 Signorini 接觸模型,利用該模型進行了有限元仿真分析,并建立了基于支持向量機(support vector machine,SVM)智能算法的接觸壓強計算模型;又采用基于神經網絡的磨削接觸力模型,對壓力進行分析和預測。為了得到曲面工件磨削的接觸壓強分布,張雷等[3-4]將圓柱形接觸輪與工件接觸視為赫茲接觸,開展了其表面去除模型的研究,盡管各向同性彈性體之間的接觸符合赫茲定律三準則,但并未考慮接觸輪的輪轂對接觸壓強分布的影響。王亞杰[5]開展了壓力、接觸輪對接觸壓強分布影響規律的研究與實驗,卻未總結出壓力、接觸輪等因素對接觸寬度和最大接觸壓強的影響規律。SUN等[6-7]將赫茲接觸理論引入到表面開槽接觸輪與工件的接觸中,其有限元仿真分析以及實驗測量結果表明赫茲理論計算的理論值誤差較大,不適用于開槽接觸輪接觸時的情況。劉斐等[8]針對彈性力學平面問題,采用復變函數解法求解了接觸區域的壓強分布規律。
上述文獻尚未充分驗證赫茲接觸在砂帶磨削中應用的準確性。本研究針對圓柱接觸輪,進行砂帶磨削接觸壓強分析,研究接觸輪厚度比、橡膠硬度和接觸壓力對接觸壓強的影響,并開展平面試件和圓柱試件磨削驗證實驗。
1 砂帶磨削接觸模型
1.1 赫茲接觸模型
赫茲提出,兩曲面物體在適當作用力下接觸并壓緊,材料在初始接觸點的附近發生局部變形,接觸區域為橢圓形,接觸壓強按半橢圓球分布[9-10],如圖1、圖2所示。
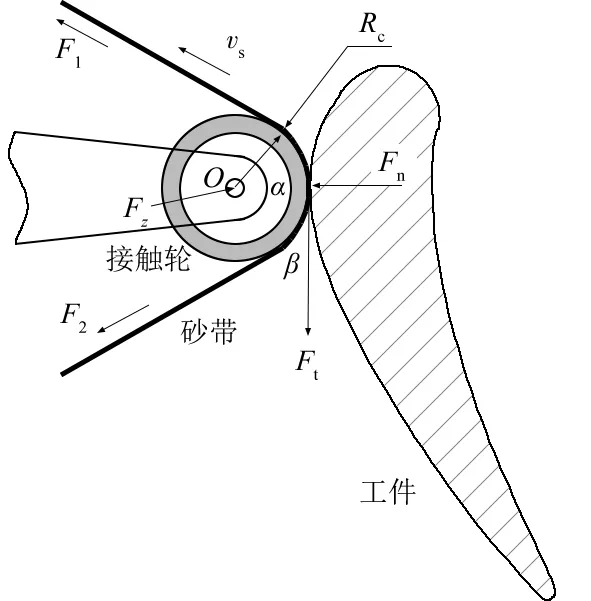
圖1 接觸輪與工件接觸受力示意圖
赫茲接觸理論滿足如下基本假設[9]:(1)接觸區域發生小變形;(2)接觸面呈橢圓形;(3)相接觸的物體可被視為是彈性半空間,接觸面上只作用有分布的垂直力。
在葉片砂帶磨削加工過程中,橡膠接觸輪與葉片的接觸壓力很小(低于10 N)。根據橡膠的應力-應變曲線,接觸輪的橡膠處于較小應力下,應力和應變近似為線性關系。實驗發現,二者接觸面為橢圓形。
由圖1可知:接觸輪繞著軸O旋轉,盡管砂帶與葉片之間有摩擦力Ft,但是,接觸輪并不承受這一摩擦力,而只承受磨削壓力Fn。
F1·sinα=Ft+F2·sinβ
(1)
式中:α和β分別為F1、F2與Ft的夾角。
在數值上有:
Ft=F1-F2
(2)
因此,葉片砂帶磨削狀態近似滿足赫茲接觸理論的基本假設。圖2中,a和b為橢圓形接觸區域的長半軸和短半軸,p0為最大接觸壓強。
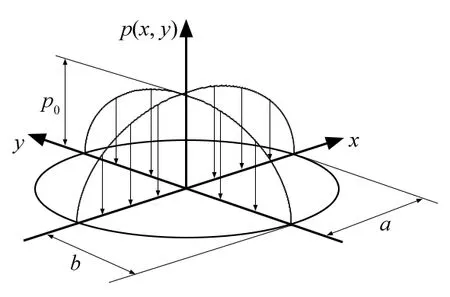
圖2 半橢圓球面壓強分布
當施加壓力為Fn時,接觸最大壓強p0可以表示為:
(3)
接觸區域的接觸壓強分布p(x,y)呈半橢圓球形狀分布。
(4)
(5)
1.2 有限元接觸模型
橡膠是一種大變形和高彈性的超彈性材料[8-10],在外力作用下發生較大形變,外力撤銷后可以恢復到原來的形狀。在接觸輪的輪轂上包裹一定厚度的橡膠,磨削過程中可起到良好減震效果。
采用Mooney-Rivlin模型分析和計算橡膠材料的力學性能。當應變不超過150%時,Mooney-Rivlin模型[11-13]中應變能函數W可近似表述為:
W=C10(I1-3)+C01(I2-3)
(6)
式中:I1和I2分別為第一和第二Green應變不變量,參數C10和C01均為材料實驗數據的回歸系數。橡膠材料參數[9]如表1所示。
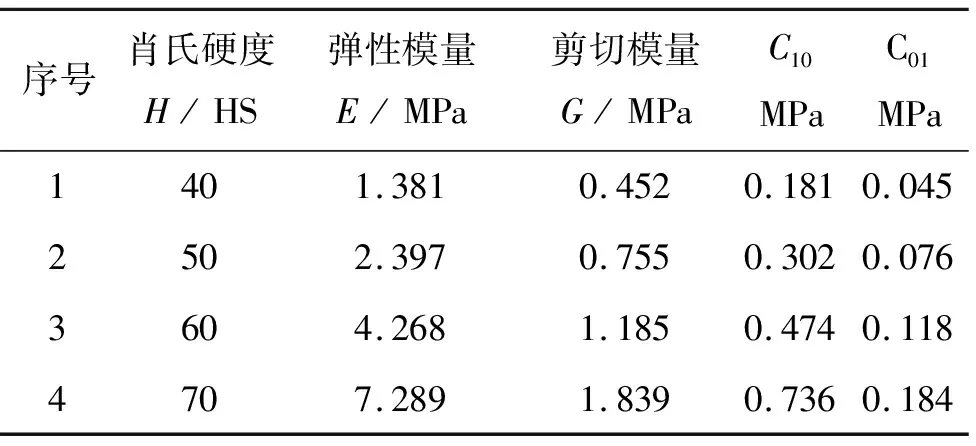
表1 橡膠材料仿真參數
為了便于實驗和測量,選用平面和圓柱工件進行分析。接觸區域和接觸壓強呈對稱分布,只需建立接觸輪的1/2有限元模型。相對于橡膠的變形量,輪轂和工件的變形可以忽略不計,將其簡化為剛體。細化接觸區域的網格,尺寸大約為0.05 mm,如圖3所示。
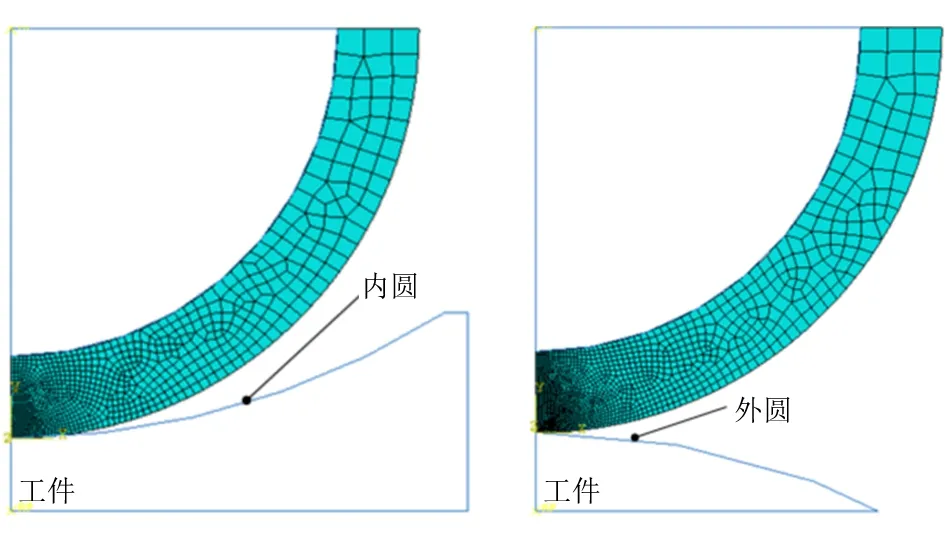
圖3 砂帶磨削有限元接觸模型
2 結果與分析
橡膠接觸輪與工件接觸的應力云圖如圖4所示。為了分析厚度比、橡膠硬度和接觸壓力等參數對接觸壓強分布規律的影響,在分析結果中獲取接觸區域的節點應力,繪制接觸區域的應力變化曲線。
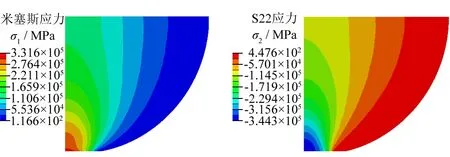
圖4 橡膠接觸輪有限元模型應力云圖
厚度比為橡膠厚度與接觸輪半徑的比值。圖5所示為不同厚度比對接觸壓強分布規律的影響。由圖5可知:對于不同的厚度比rt,沿著x軸方向,有限元分析獲得接觸區域的壓強均呈半橢圓形分布;厚度比越小,最大接觸壓強越大,而接觸寬度越小;當厚度比rt為20%時,有限元分析得到的壓強分布與赫茲接觸模型的理論值最接近。
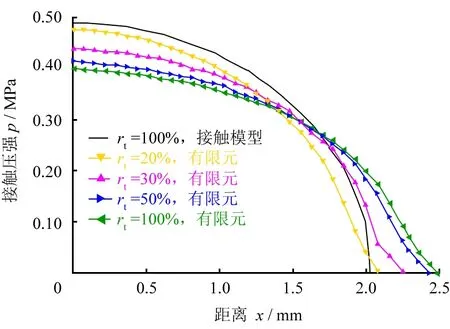
圖5 厚度比對接觸壓強分布規律的影響
圖6為不同橡膠硬度對接觸參數的影響:橡膠肖氏硬度越大,最大接觸壓強越大而接觸寬度越小;當橡膠肖氏硬度H小于60 HS時,隨著橡膠硬度的增加,接觸寬度急劇減小;當橡膠肖氏硬度H大于60 HS時,隨著橡膠硬度的增加,接觸寬度變化較為平緩。
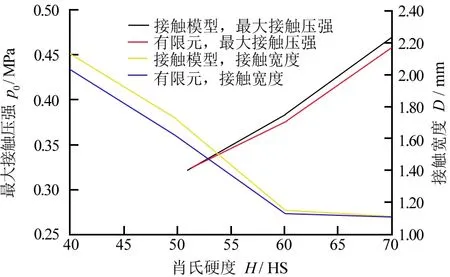
圖6 不同橡膠硬度對接觸參數的影響
圖7所示為不同接觸壓力對法向接觸參數分布的影響。由圖7可以看出:由于橡膠的非線性,隨著接觸壓力Fn的增大,最大接觸壓強和接觸寬度逐漸增大,而有限元模型與赫茲接觸模型分析得到的最大接觸壓強和接觸寬度數據之間的差距逐漸增大;當接觸壓力達到50 N時,最大接觸壓強差達到了0.16 MPa,接觸寬度相差0.87 mm。
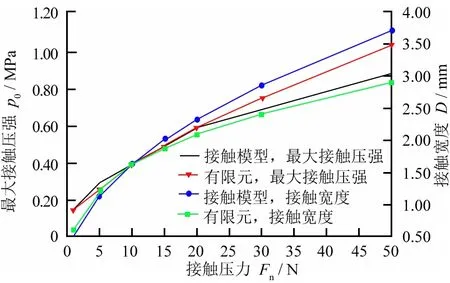
圖7 接觸壓力對接觸參數的影響
葉片表面由凹、凸曲面組成,葉片表面的曲率影響接觸壓強的分布,如圖8所示。對于凹曲面(曲率半徑為負數),曲率半徑越小,有限元模型數據與赫茲接觸理論結果之間的差距越小;對于凸曲面(曲率半徑為正數),在相同的接觸壓力下,最大接觸壓強差別較大,這是因為凸曲面與圓柱接觸輪的接觸面積更小。
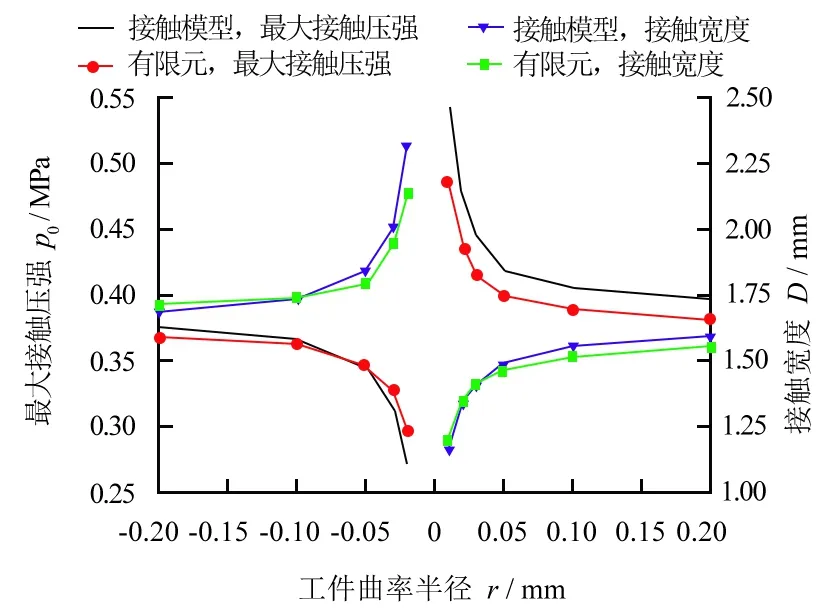
圖8 不同工件曲率半徑對接觸參數的影響
3 接觸實驗
3.1 與平面工件的接觸測試
為便于測試磨削過程中工件表面的接觸寬度,設定工件寬度小于接觸輪的厚度,放置位置如圖9所示。施加的壓力在工程許可范圍內,采用不同的肖氏硬度H和接觸輪半徑R,磨削后測量的接觸寬度如圖10所示。

圖9 磨削平面試件示意圖

圖10 接觸測試的平面試件
圖11顯示了接觸寬度隨著接觸壓力呈非線性增大的變化規律,其測量值與有限元分析和赫茲接觸模型理論值均十分接近。
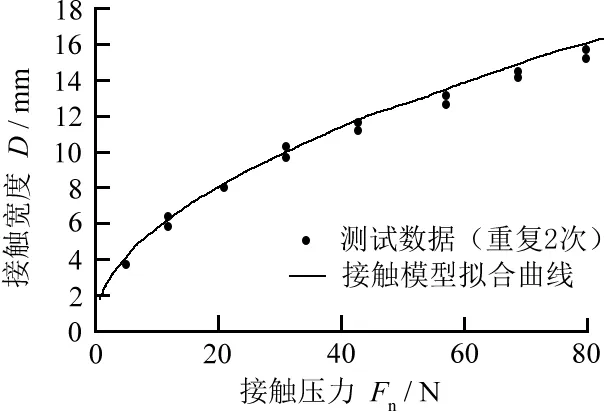
(a)H=65 HS,R=140 mm
3.2 與圓柱工件的接觸測試
赫茲接觸理論表明:當2個圓柱物體接觸且軸線平行時,接觸區域為矩形;當2個圓柱物體接觸但軸線不平行時,接觸區域為矩形或橢圓形。為了便于實驗和測量,將圓柱試件的軸線擺放在與接觸輪軸線垂直的位置,如圖12所示。

圖12 磨削圓柱試件示意圖
實驗用接觸輪半徑為140 mm,橡膠的肖氏硬度為45 HS,圓柱試件半徑為10 mm。圖13所示為接觸后的圓柱試件表面。由圖13可見:接觸區域為橢圓形,橢圓形的長半軸與圓柱試件的軸線同向。這是因為接觸輪的半徑大于圓柱試件的半徑。

圖13 接觸后的圓柱試件表面
圖14所示為接觸區域橢圓接觸斑尺寸隨接觸壓力的變化。從圖14可以看出:隨著接觸壓力的增大,長、短半軸的長度均呈非線性增大;長、短半軸的測試數據均與赫茲接觸理論值保持一致;隨著接觸壓力的增大,相比于長半軸,短半軸增量平緩。這是因為圓柱試件的半徑遠小于接觸輪的半徑,除了接觸壓力外,其他實驗條件未改變,長、短半軸的比值也是恒定的。
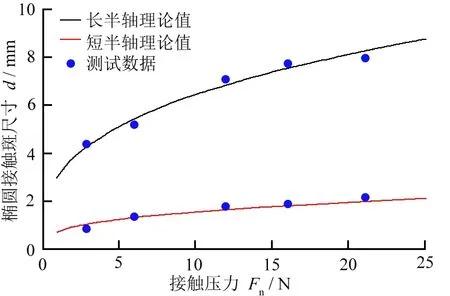
圖14 橢圓接觸斑尺寸隨接觸壓力的變化
4 結論
從赫茲接觸的基本假設角度,分析砂帶模型接觸狀態;通過有限元分析和實驗驗證砂帶磨削接觸采用赫茲接觸理論的準確性,得出如下結論:
(1)用于磨削的切向力Ft被張緊力抵消,并未作用在接觸輪上。忽略影響較小的因素,砂帶磨削接觸狀態基本符合赫茲接觸理論。
(2)通過ABAQUS有限元軟件,建立接觸輪與工件接觸的有限元模型,分析橡膠硬度、厚度比、接觸壓力以及工件曲率半徑等因素對最大接觸壓強和接觸參數的影響。當厚度比為20%和橡膠肖氏硬度為70 HS時,橡膠接觸輪的接觸壓強分布與赫茲接觸理論之間的誤差最小。當接觸壓力低于15 N時,有限元模型與赫茲接觸理論數據曲線幾乎重合,滿足工程應用要求。相對于凸曲面,接觸輪與凹曲面工件接觸誤差較小。
(3)通過平面和圓柱工件與圓柱接觸輪接觸的測試實驗,驗證了建立的有限元模型和接觸模型的準確性,說明赫茲接觸理論適用于砂帶磨削。

