動態價格下含時滯的Logistic漁業模型的Hopf分支

張 桓，張 悅

(東北大學 理學院， 沈陽 110819)

隨著人類對海洋漁業的生物資源需求的增加，合理的捕撈及有效利用市場資源越發重要。海洋管理需要實現可持續開發一直是生物學家與經濟學家關注的熱點問題[1-2]。考慮一個標準的漁業開放模型[3]，研究文獻經常將價格考慮為不變量。1954年Gordon[4]把價格成本引進生物經濟模型，假設單位價格和捕獲成本為常數，而漁業的價格和市場結構變化迅速，市場價格受漁業供給關系影響。針對管理市場價格相互作用的需要，建立了漁業經濟模型[5]，因此，在模型的基礎上添加了市場上資源價格的動態變化。根據文獻[6]，價格的變化取決于需求函數(魚類的銷售量)和供給函數(漁獲量)之間的關系。文中假設價格變化快于魚類庫存量的變化，因此通過一個小的正參數s來調整價格動態，稱為價格動態變化速度[7]。該參數反映了市場價格的彈性變化。

不僅如此，在漁業模型中，時滯現象的考慮也成為新的突破點。描述不同生態相互作用的時滯總是不同的，因此分別討論每種時滯對魚類種群和市場價格的動力學的影響有助于確立合適的管理措施。Celik[8]研究了一類種群具有時滯的模型，以時滯τ為參數，分析了模型唯一正平衡點的局部漸近穩定性與Hopf分支的存在性。魚類種群與市場價格的動態發展趨勢不僅依賴于當前的狀態，還依賴于過去或未來某一時間段的狀態影響。引入時滯會影響系統的穩定性并產生分支，而系統中分支的出現將使漁業的變化規律更加的復雜。葉志勇等[9-10]探討了經典生物模型的穩定性與Hopf分支。劉聰穎等[11-12]根據對兩類具有時滯的種群動力學模型的定性分析，結合穩定性理論討論了正平衡點的全局漸近穩定的充分條件。秦麗等[13-14]討論了雙時滯在階段結構的模型中平衡點的局部漸近穩定性及Hopf分支。因此，本文選用具有時滯的微分方程分析動態模型。俞美華[15]研究了價格變化的生物種群經濟捕獲模型，并在此基礎上建立具有時滯的經濟捕獲模型，采用時滯方程的穩定性理論對正平衡點穩定性進行分析，從而得出時滯會改變平衡點穩定性的結論。

本文從新型動態價格下種群的Logistic生長模型出發，根據具有雙時滯和價格的復雜性的生物經濟模型，通過改變時滯和復雜性參數來檢驗局部穩定性和存在性。研究了Hopf分支方向和分支的穩定性，分析了生物捕撈業復雜性和多時間延遲對生物經濟捕食者-種群模型動力學的影響。

1 模型的建立

考慮一個有關漁業在動態價格下[16]具有雙時滯的Logistic模型，系統描述如下：

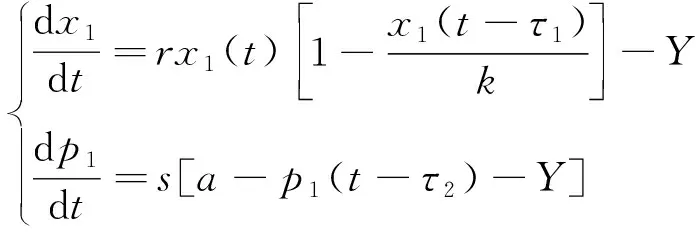
(1)

式中：x(t)是在t時刻的魚群儲存量(t)，x(0)=x0>0；p(t)是儲存量在t時刻的單價(萬元/t)，p(0)=p0>0；a-p(t)為正線性需求函數[17]；Y是常數捕獲率(t/天)；r為魚群每日的內稟增長率；τ1、τ2分別表示魚群和市場價格的時間延遲；k為環境承載能力(t)；s為價格動態變化速度；a為正常數參數，表示市場容量。

2 局部穩定性與Hopf分支

以下討論正平衡點E的局部漸近穩定性與在平衡點E處Hopf分支的存在性。

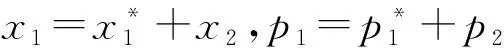
(2)

其雅克比矩陣為：

系統(2)對應的特征方程：

(3)

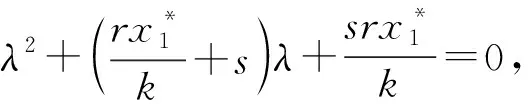
現在討論以下5種情況下，2個時滯對正平衡點E穩定性的影響。

1) 只有魚類種群受時滯影響，即τ1>0，τ2=0。

在此情況下，特征方程(3)可簡化為：

λ2+(Ae-λτ1+s)λ+sAe-λτ1=0

(4)

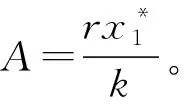
假設λ=iω1為方程的一個根，將iω1(ω>0)代入方程(4)中，則有

(5)

分離上述方程的虛部與實部，得：

(6)

把上述方程的兩端平方相加，得到關于ω1的方程：

(7)

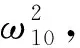
(k=0，1，2，…)，對應的τ1k>0使得方程(4)有一對純虛根±iω10。

運用Butler引理[18]，可以得出在s2+A2<6s2A2條件下，當τ1<τ10時，模型(2)的內部平衡點是局部漸近穩定的。

接下來，對方程(4)求關于τ1的導數：

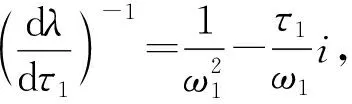
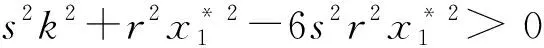
當|τ1-τ10|<<1時，發生Hopf分叉。也就是說，模型(2)有一個周期解分支，該分支來自正平衡點E在τ1=τ10附近的分支。

當τ1>τ10時，模型(2)的正平衡點E是不穩定的。

2) 只有市場價格受時滯影響，即τ1=0，τ2>0。

類似于1)的分析過程，有下述結果：

當s2+A2>6s2A2時，特征方程存在唯一正實根ω20。 其對應的時滯為：

(k=0，1，2，…)

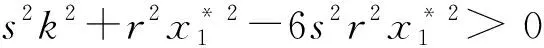
當τ2>τ20時，模型(2)的正平衡點E是不穩定的。

3) 當魚類種群與市場價格均受時滯影響，τ1為參數，即τ1>0，τ2∈[0，τ20)，并且τ1≠τ2。

在此情況下，特征方程為:

λ2+(Ae-λτ1+se-λτ2)λ+

sAe-λ(τ1+τ2)=0

(8)

設λ=iω11(ω11>0)為方程的一個根，將iω11代入方程(5)中，則：

sAe-iω11(τ1+τ2)=0

(9)

分離上述方程的虛部與實部，并將所得方程兩邊平方相加，得到關于ω11的方程：

2sA2ω11sinω11τ2+s2A2=0

(10)

當滿足s2+A2>6s2A2時，關于上述方程存在唯一正實根ω11。

(m=0，1，2，…)

對應的τ1m>0使得方程(8)有一對純虛根±iω11。

運用Butler引理[18]可以得出：在s2+A2<6s2A2條件下，當τ1>0，τ2∈[0，τ20)時，模型(2)的內部平衡點是漸近穩定的。

對方程(8)求關于τ1的導數，并計算：

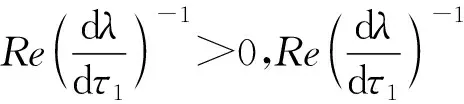
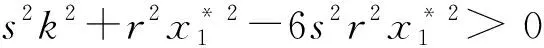
當τ1∈[0，τ10)，τ2∈[0，τ20)時，

模型(2)的正平衡點E是局部漸近穩定的；

當τ1=τ10時，發生Hopf分叉。也就是說，模型(2)有一個周期解分支，該分支來自于正平衡點E在τ1=τ10附近的分支。

當τ2∈[0，τ20)，τ1>τ10時，模型(2)的正平衡點E是不穩定的。

4) 當魚類種群與市場價格均受時滯影響，τ2為參數，即τ1∈[0，τ10)，τ2>0，并且τ1≠τ2。

類似于2.3的分析過程，有下述結果：

當滿足s2+A2>6s2A2時，關于方程：

2s2Aω22sinω22τ1-s2A2=0

(11)

存在正實根ω22，其對應的時滯為：

(n=0，1，2，…)

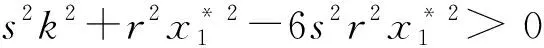
當τ1∈[0，τ10)，τ2∈[0，τ20)時，

模型(2)的正平衡點E是局部漸近穩定的；

當τ2=τ20時，發生Hopf分叉。也就是說，模型(2)有一個周期解分支，該分支來自于正平衡點E在τ2=τ20附近的分支。

當τ1∈[0，τ10)，τ2>τ20時，模型(2)的正平衡點E是不穩定的。

5) 當魚類種群與市場價格均受相同時滯影響，即τ1=τ2=τ(τ>0)

此時，特征方程變成：

λ2+(A+s)λe-λτ+sAe-2λτ=0

(12)

在方程(12)兩邊同時乘以eλτ，可得:

λ2eλτ+(A+s)λ+sAe-λτ=0

(13)

假定λ=iω(ω>0)是(13)的根，則有：

-ω2eiωτ+(A+s)iω+sAeiωτ=0

(14)

分離上述方程的虛部與實部：

(15)

將上述方程兩邊平方相加，得到關于ω的方程：

ω4+s2A2-2ω2sA(cos2ωτ-sin2ωτ)-

(A+s)2ω2=0

(16)

當滿足s2+A2-4s2A2+2As>0時，關于上述方程存在唯一正實根ω0。

(j=0，1，2，…)

對應的τj>0使得方程(12)有一對純虛根±iω0。

在s2+A2-4s2A2+2As<0條件下，當τ<τ0=min{τj}時，模型(2)的內部平衡點是漸近穩定的。

假設λ(τ)=x(τ)+iω(τ)是方程(12)在τ=τ0處的根。則方程(12)關于τ的導數為：

從而得到橫截性條件：

定理5對于模型(2)，若s2+A2-4s2A2+2As<0成立，則：當τ<τ0，

模型(2)的正平衡點E是局部漸近穩定的；

當τ=τ0時，發生Hopf分叉。也就是說，模型(2)有一個周期解分支，該分支來自正平衡點E在τ=τ0附近的分支。

當τ>τ0時，模型(2)的正平衡點E是不穩定的。

3 數值模擬算例

令模型(2)中，r=0.015，k=1 802.6，Y=7，a=800，s=0.005，則模型(2)存在平衡點E1，這些系數滿足上述條件，當不考慮時滯時，正平衡點E1漸近穩定，如圖1所示。

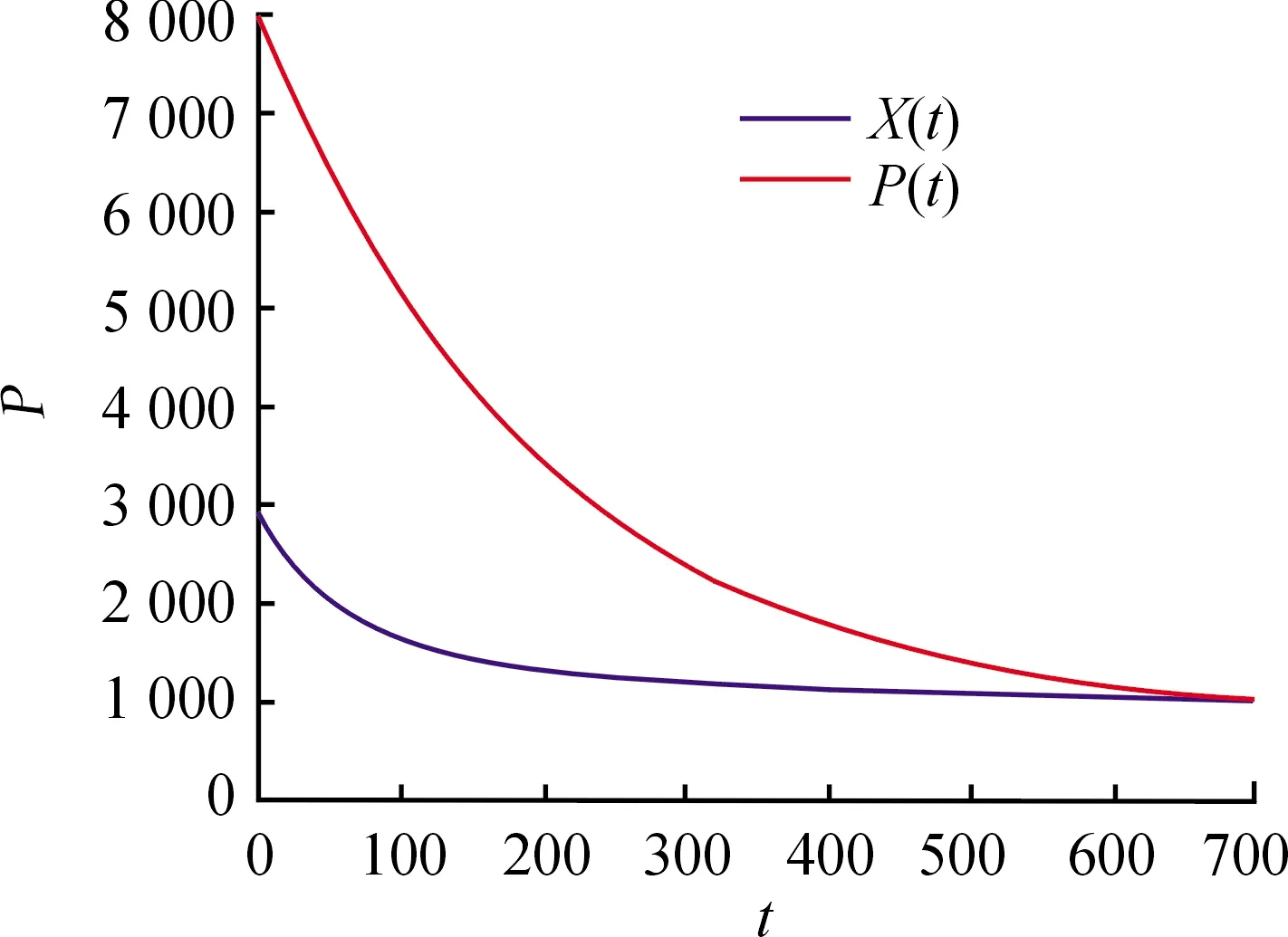
圖1 當τ1=τ2=0時，平衡點E1漸近穩定曲線

令模型(2)中，r=0.015，k=1 703.2，Y=7，a=800，s=0.071，則模型(2)存在平衡點E1。當只有市場價格受時滯影響時，τ1=0，基于第2部分的分析，當這些系數滿足上述條件，根據計算可得ω20，τ20。圖2表明：當τ1=0，τ2=10.35時，平衡點E1漸近穩定；當τ1=0，τ2穿過τ20時一個穩定的周期解從平衡點E1分支出來。

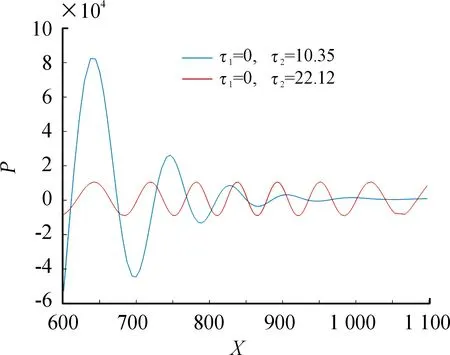
圖2 當τ1=0，τ2=10.35時，系統出現漸近穩定曲線；當τ1=0，τ2=22.12時，系統出現穩定的周期解曲線

令模型(2)中，r=0.015，k=1 802.6，Y=7，a=800，s=0.989，則模型(2)存在平衡點E1。當只有魚類種群受時滯影響時，τ2=0，基于第2部分的分析，當系數滿足上述條件，根據計算可得ω10，τ10。圖3表明：當τ1=39，τ2=0時，平衡點E1漸近穩定；當τ2=0，τ1穿過τ10時一個穩定的周期解從平衡點E1分支出來。

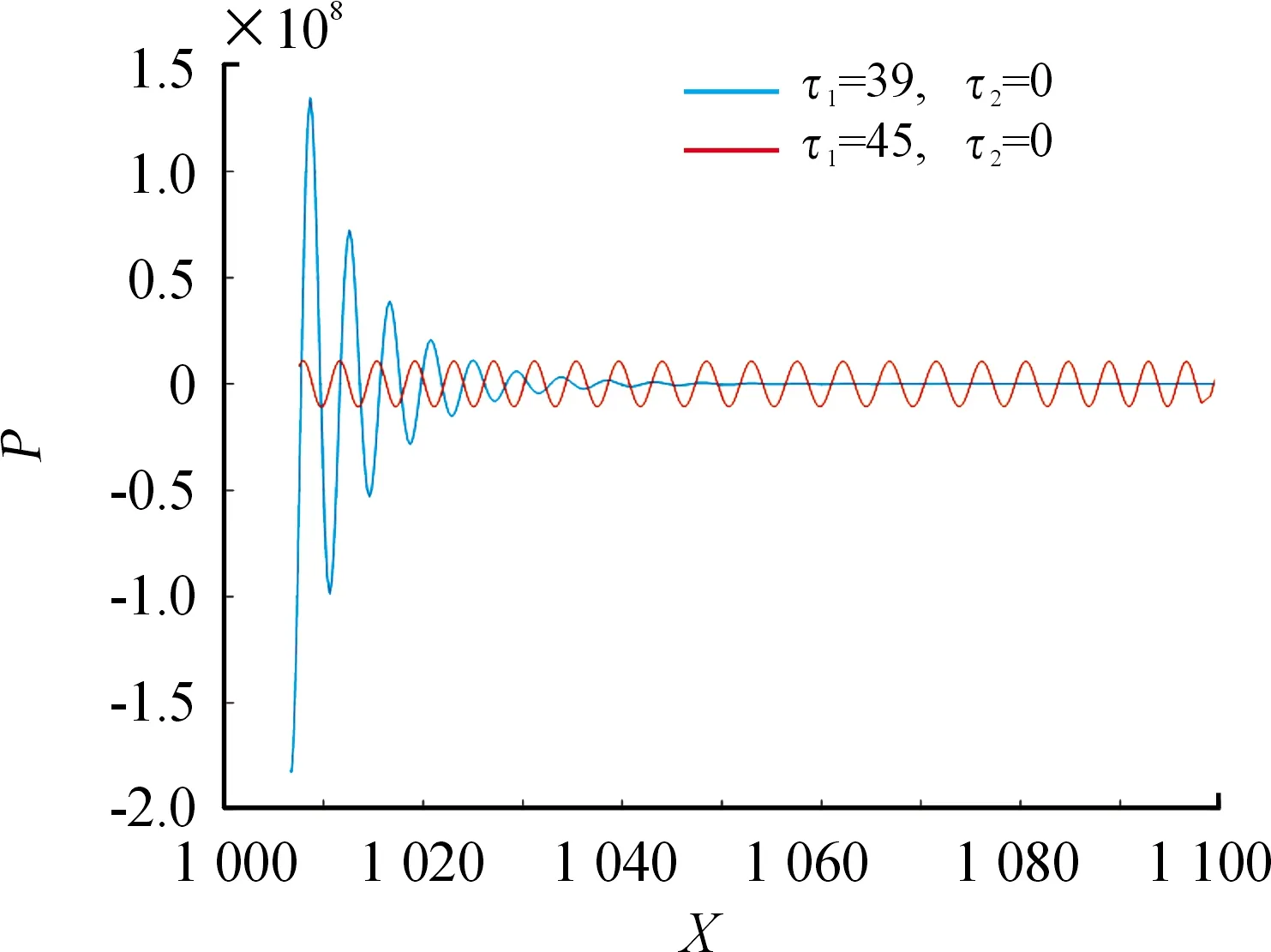
圖3 當τ1=39，τ2=0時，系統出現漸近穩定曲線；當τ1=45.3，τ2=0時，系統出現穩定的周期解曲線

令模型(2)中，r=0.015，k=1 602.6，Y=7，a=800，s=0.076，則模型(2)存在平衡點E1，對固定的時間延遲τ1=2，當系數滿足上述條件，可計算得出ω22，τ20。圖4表明：當τ1=2，τ2=16時，平衡點E1漸近穩定；當τ1=2，τ2穿過τ20時一個穩定的周期解從平衡點E1分支出來。

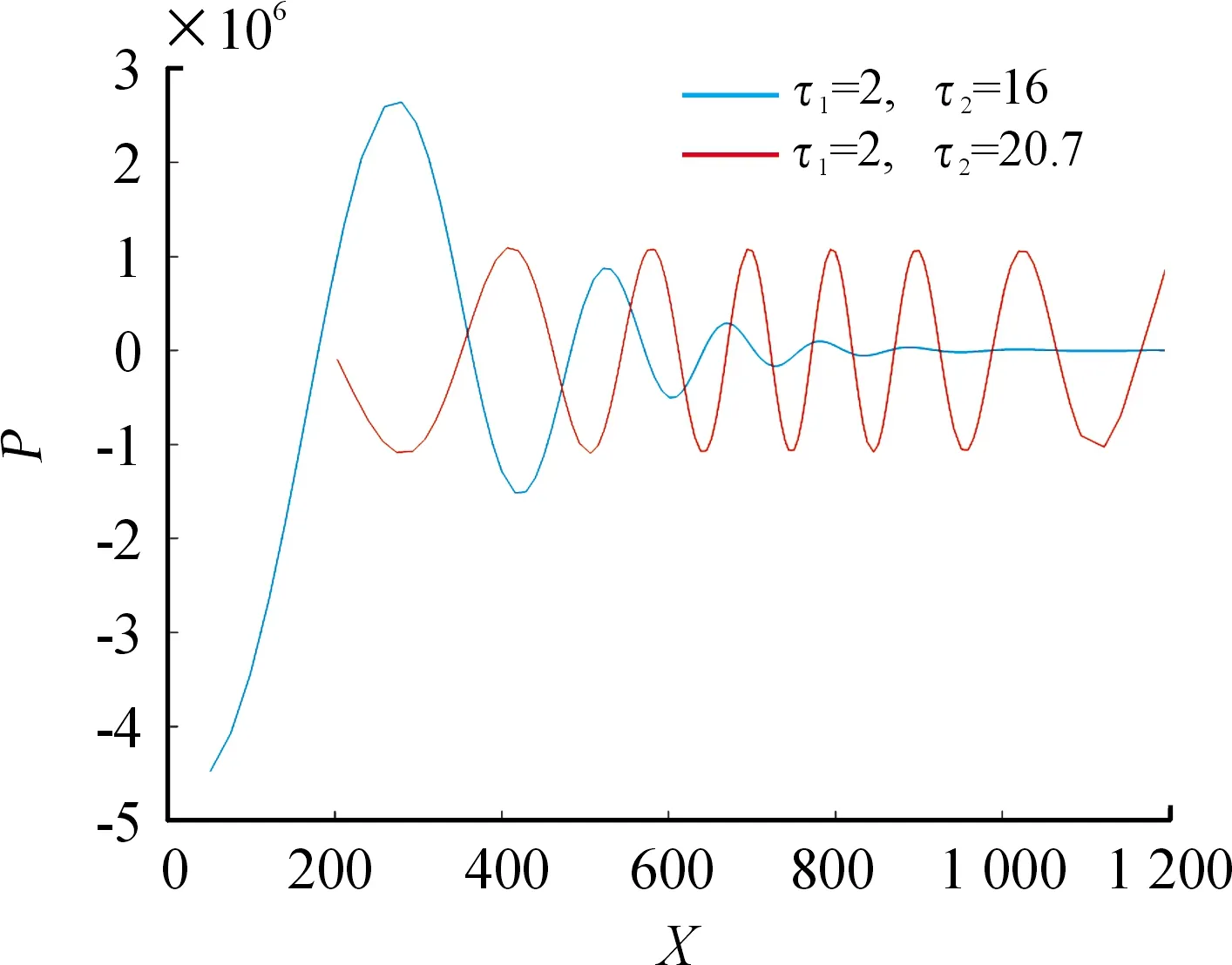
圖4 當τ1=2，τ2=16時，系統出現漸近穩定曲線；當τ1=2，τ2=20.7時，系統出現穩定的周期解曲線

4 結論

1) 研究分析，當模型(2)存在正平衡點時，在不考慮時滯即τ1=τ2=0的情況下，此時正平衡點漸近穩定。雙時滯在5種不同情況下會影響模型正平衡點的穩定性。

2) 當只有市場價格(或只有魚類種群受時滯影響)時，若上述條件成立，則當時滯滿足τ1=0，τ2∈[0，τ20)(或τ1∈[0，τ10)，τ2=0)時，漁業模型(2)的正平衡點E是局部漸近穩定的，當τ2=τ20(或τ1=τ10)時，發生Hopf分叉，此時穩定的周期解出現。

3) 當魚類種群與市場價格均受時滯影響，τ1為參數，若上述條件成立，則當時滯τ1>0，τ2∈[0，τ20)時，漁業模型(2)的正平衡點E是局部漸近穩定的，意味著此時漁業種群與市場價格都趨于穩定狀態；當τ1=τ10時，發生Hopf分叉。也就是說，模型(2)有一個周期解分支，該分支來自于正平衡點E在τ1=τ10附近的分支。

4) 而當漁業種群與市場價格均受相同時滯影響，即τ1=τ2=τ，當滿足相應條件時，模型(2)的內部平衡點是漸近穩定的。說明當時滯達到某個臨界值時，會影響種群與市場價格平衡的穩定性并導致Hopf分支的出現。

5) 通過時滯的影響，漁業活動的穩定性和市場價格進一步得到了保證，在適當的時候對于最優捕魚期和生物休漁期的制定管理措施有一定的幫助。本模型的一個重要局限性是沒有考慮環境影響的隨機性，接下來將在模型的基礎上引入隨機變量研究系統的穩定性。