積木模型研究原子核質量

吳雨澤 王偉紅

上海市進才實驗中學 上海 200135

一、前言

原子核質量是原子核的基本性質之一,它直接反映了核內所有的相互作用,是強相互作用、電磁相互作用和弱相互作用的共同結果。高精度原子核質量數據對人們了解核結構和基本對稱性有重要的意義,是核結構和核反應研究的基礎課題,也是核天體物理研究的重要輸入量。原子核質量的深入研究對于探索豐中子核的奇特結構以及研究超重核結構及其衰變特性都具有重要意義,可以提供一些關鍵原子核的質量和壽命等基本特征[1-3]。在天體物理中,原子核的質量可以協助了解恒星的形成、演化和其最終的命運,而且精確的質量值將可以延伸到核物理之外的各個領域之中,得到更廣泛的應用例如在計量學、量子電動力學、基本電荷等。一些核物理學家已經采用深度學習、神經元算法等對原子核質量進行了研究[5],但精度仍然不能超過實驗的測量精度。

本項目著眼建立新的算法模型,用過積木模型替代液滴模型中的同位旋效應,試圖從理論上給出更符合實驗數據的的原子核質量。

二、理論模型

（一）液滴模型

有著90年歷史的液滴模型極其簡單,但它經受住了時間的考驗這是一個值得關注的事實。原因在于,LDM認為原子核為一個不可壓縮的液滴,由兩種量子流體組成帶電的Z個質子與不帶電的N個中子,所計算的結合能可以根據Z和N的變化二平穩變化。它將中子和質子比作液滴中的分子,小液滴的質量主要和它的體積成正比,該模型能較為準確的給出原子核的性質,所以至今仍在研究原子核質量、研究超重元素合成,研究中子星的內部結構中廣泛應用。1935年魏扎克依據液滴模型提出一個計算原子核質量的公式:

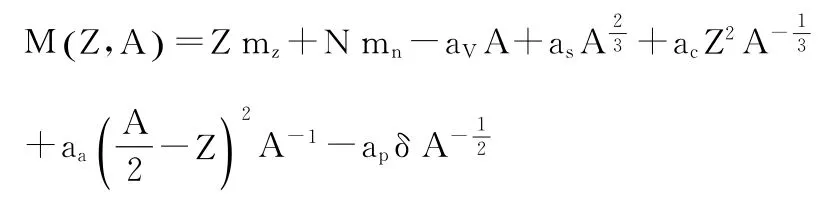
本文選取研究了質子數分別為20,30,40,50的Ca、Zn、Zr和Sn元素的同位素鏈條進行研究,20-50剛好包含兩個完整的大殼層,研究結果可以復制到其它殼層。四條同位素鏈,總的結合能都隨著質量數的增加而增加,這表現出原子核的“液滴”這一特性,但增加的幅度有所減慢,這主要是因為隨著原子核的體積增大,庫倫能和表面能的影響越來越大。

我們用液滴模型的表1參數組計算了Z=20、30、40、50的同位素的原子核總結合能與實驗值的百分比誤差?？梢钥闯鲆旱文Ｐ徒o出的總結合能,百分比誤差在4%以內,平均誤差為1.11%,說明液滴模型可以較好的描述原子核中的結合能。在中子數和質子數相等時,誤差較小,中子和質子數目相差越多,誤差越大。說明液滴模型在描述遠離β穩定線的核素時有一定困難,而遠離β穩定線的核素同位旋效應占據了主要地位,所以只有修改模型中的同位旋效應項才能給出符合實驗的原子核質量。

（二）積木模型

由以上對液滴模型的分析,我們可以看出液滴模型在研究中子和質子對稱的時候效果較好,中子和質子很不對稱的情況下誤差較大。為了解決這個問題,我們建立了積木模型:考慮到相同的積木搭兩座大樓,如果樓層數相同最穩定,樓層數相差越大,越不穩定,越容易被推倒,這和液滴模型中的同位旋項相類似。我們采用兩種積木（中子N和質子Z）搭建原子核,設每塊中子、質子積木塊的質量分別為mn和mz,考慮到質子之間有庫倫排斥力,我們設定兩種積木塊的大小不同,寬度和高度分別為xn和xz、hn和hz

圖1 積木模型示意圖

兩棟樓房水平方向的重心滿足杠桿平衡條件（其中x為重心的x坐標）:

解得x=Zmz（xn+xz）/2（Zmz+Nmn）,要想推動該積木塊,需要滿足的杠桿平衡條件為:

帶人x并化簡得到

F=g{（2xn+xz）Zmz+xnNmn}/2Nhn。其中mz=938.272Me V/c2,mn=939.565 MeV/c2,設mz≈mn,上式可化簡為:F=an{bZ/N+1}。其中an為跟hn相關的參數,b為2+xz/xn,同理可得當Z＞N時F=az{bN/Z+1}?？紤]到液滴模型中的體積項,我們最終給出了3參數的積木模型

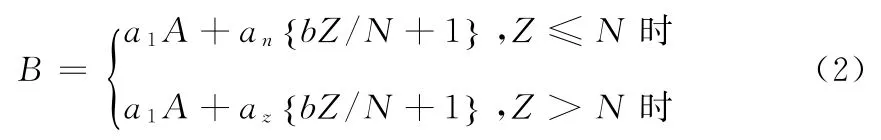
三、結果與討論

我們通過最小二乘法計算了Ca、Zn、Zr和Sn同位素的總的結合能,并與實驗數據對比,得到參數a1,an（az）,b的值列于表1:

表1 積木模型參數表

其中a1為體積項系數,提供結合能的主要部分,an和az表征中子和質子不同的同位旋效應,因為質子有庫倫斥力,所以其系數為負;b為同位旋效應的強度系數,其數值較大,可以很好的表征遠離β穩定線核素的性質。

積木模型計算得到的結合能與實驗值的比較,可以看出在對比液滴模型少一個參數的情況下,原子核的總的結合能與實驗符合的較好,積木模型可以作為計算原子核質量的一種嘗試。圖中看出在輕質量核素符合的較好,重核素中遠離β穩定線核素誤差較大,這是因為重核素表面相互作用逐漸增強,重核素的四級形變越來越強,考慮重核素的四級形變修正可以進一步降低誤差。

四、小結

本文在液滴模型的基礎上,引入了描述原子核同位旋效應的積木修正項,在減少一個參數的情況下,使得用液滴模型計算原子核質量的精確度有所提高,該模型可以給出更多原子核中核子-核子間相互作用的信息,對了解原子核內部結構有一定的物理意義。