提煉基本圖形 培養(yǎng)幾何直觀

郭海英

（杭州學軍中學教育集團文淵中學，浙江 杭州 310000）

對“幾何直觀”的理解

對它的認識：“直觀”就是當人們接觸事物時，借助于觀察、經(jīng)驗、想象等所產(chǎn)生的對事物及其關(guān)系直接的感知與認識。而幾何直觀則是借助于見到的或想到的幾何圖形的形象關(guān)系產(chǎn)生的對事物的性質(zhì)或數(shù)量關(guān)系的直接感知與認識，幾何直觀是一種運用圖形認識事物的能力。標準指出：“幾何直觀”是指利用圖形描述和分析問題，借助幾何直觀可以把復雜的數(shù)學問題變得簡明、形象，有助于探索解決問題的思路，預測結(jié)果。幾何直觀可以幫助學生直接地理解數(shù)學，在整個數(shù)學學習過程中發(fā)揮重要作用，

它的意義：20 世紀最偉大數(shù)學家希爾伯特在名著《幾何直觀》一書中談到：

第一層意思，圖形可以幫助刻畫和描述問題。一旦用圖形把一個問題描述清楚，就有可能使這個問題變得直觀、簡單。

第二層意思，圖形可以幫助發(fā)現(xiàn)、尋找解決問題的思路。

第三層意思，圖形可以幫助表述一些結(jié)果，可以幫助記憶一些結(jié)果。

如何幫助學生建立幾何直觀

第一 要充分的發(fā)揮圖形帶來的好處。

第二 要讓學生養(yǎng)成一個畫圖的好習慣。

第三 重視變換，讓圖形動起來，把握圖形與圖形之間的關(guān)系。

第四 要在學生的頭腦中留住些圖形(比如基本圖形）。

無論是在“圖形與幾何”領(lǐng)域的學習還是在其他領(lǐng)域的學習中，都應(yīng)重視幾何直觀的培養(yǎng)。

在中考中有許多試題是根據(jù)基本圖形來巧妙設(shè)置的，這樣既考查學生提煉圖形和運用圖形的能力，更是對“幾何直觀”的一種培養(yǎng)。基本圖形具有廣闊的拓展空間，根植于基本圖形的試題屢見不鮮。挖掘基本圖形，有助于更好的培養(yǎng)發(fā)散性思維，提高學生分析問題解決問題的能力。今天我們通過展示一些案例跟大家談?wù)勗诘诙啅土曋刑釤捇緢D形的方法。

（一）K 字型圖

案例1.如圖，AB ⊥BD 于點B，CD ⊥BD 于點D，P 是BD上一點，AP ⊥PC,且AP=PC. 你能得到什么結(jié)論？

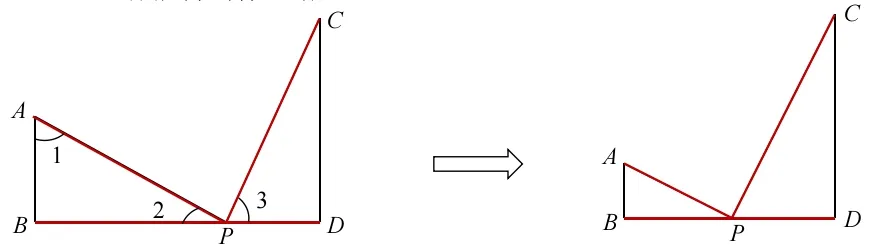
這時我們每個同學都能得出結(jié)論：有兩個全等三角形，有對應(yīng)邊相等，這個基本圖形，我們給它一個名稱叫K 字型。如果把條件AP=PC 去掉，那么就能得出兩個三角形相似。接下來用K 字型圖可以比較快的解決下面的幾個習題。

變式1.如圖，已知AB ⊥BD,CD ⊥BD,AP ⊥PC,且P為BD 中點，AB=2，BD=6，那么CD=_______直線l2過點B(0,2)且與x軸平行，直線l1與直線l2相交于點P。點E為直線l2上一點，反比例函數(shù)

案例2：在平面直角坐標系XOY中，直線l1過點A(1,0)且與y軸平行，的圖像過點E 與直線l1相交于點F。

1.若點E 與點P 重合，求k的值；

2.連接OE、OF、EF。若k＞2，且△OEF 的面積為△PEF 的面積的2 倍，求E 點的坐標；

3.是否存在點E及y軸上的點M，使得以點M、E、F為頂點的三角形與△PEF 全等？若存在，求E 點坐標；若不存在，請說明理由。

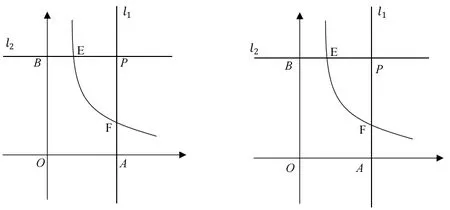
變式1：如圖，直線L1 過點A(1,0)且與y軸平行，直線L2過點B(0,2)且與x軸平行，直線L1與直線L2相交于點P.點E為直線L2上一點，反比例函數(shù)的圖像過點E 與直線L1相交于點F，存在點E及y軸上的點M，使得以M、E、F為頂點，且以EF為直角邊的三角形與△PEF 相似，則點E 的坐標____▲___.

（二）K 字圖的變形

案例2.若直線QE ∥y 軸，將含45°角的直角三角板如圖所示放置，你能夠得出什么結(jié)論？

現(xiàn)在老師已經(jīng)添了兩條輔助性，這對解決本題就不會顯得有多大難度了，可以證明兩個三角形全等，但是其實這也是前面K 字型圖的變形，也可以用K 字型圖來解答。現(xiàn)在我們來回顧一道2011年紹興的中考題24 題，這是一道很典型的以基本圖形中K 字變形圖作為解題的突破口，就可以輕松拿下了。

對中考第二輪復習教學來說，我們尤其要重視基本圖形的提煉和挖掘，如果把一道綜合題比喻成一座房子的話，那么具體的知識點就好比磚頭、鋼筋、水泥等，而基本題、基本圖形就好比一堵墻、一個房間。墻與墻之間、房子與房子之間如何搭建，就是解題的思路了。在考場上，面對每一道題目，都要求學生在較短的時間內(nèi)對解題思路作出選擇和判斷，如果熟悉一些基本圖形，無疑能提高他們探索解題思路的速度。當基本圖形直接看不出時，就能想到去構(gòu)造基本圖形。如果把這個K 字型圖的直角加以變形，我們可以把這三個角變?yōu)橄嗟龋旤c不同，但都在一條線上，構(gòu)成兩個三角形（或三個）其中兩邊上的兩個是相似，這就是我們接下來要來運用的“一線三等角”這一基本圖形。其實也是一個K字型的變形。

（三）一線三等角

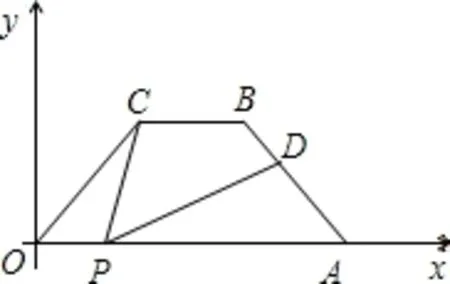
案例1 如圖所示，在平面直角坐標系中，四邊形OABC 是等腰梯形，BC ∥OA，OA=7，AB=4，∠COA=60°，點P為x 軸上一個動點，（點P 不與O、A 重合），連接CP，過點P 作PD 交AB 于點D.

1.求點B 的坐標；

2.當點P運動到什么位置時，△OCP為等腰三角形，求此時點P的坐標；

這一問題的解答是：填上常用輔助性過點B 作BE 垂直O(jiān)A,根據(jù)已知條件就可以把點B 的坐標得出，第2 小題要用到分類思想，不過在讀題目是要注意條件“x 軸上”，所以考慮的范圍要擴大到x 軸的負半軸，第3小題如果能發(fā)現(xiàn)在同一條線段上又不同頂點的三個角相等，就顯得很容易了，用“一線三等角”這個基本圖形，存在相似三角形，所以就可以通過OP×PA=OC×AD，從而求得結(jié)果。

案例2 .如圖.直角梯形OABC 的直角頂點O 是坐標原點，邊OA，OC分別在x 軸、y 軸的正半軸上.OA ∥BC，D 在BC上，，AB=3,∠OAB=45°，D 是BC上一點，CD=.E、F 分別是線段OA、AB上的兩動點，且始終保持∠DEF=45°，設(shè)OE=x，AF=y.

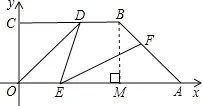
1.證明△ODE ∽△AEF，并確定y 與x 之間的函數(shù)關(guān)系；

2.當△AEF 是等腰三角形時，將△AEF 沿EF 折疊，得到△A′EF，

求△A′EF 與五邊形OEFBC 重疊部分的面積.

解決本題也是跟上面一樣的思路，不過現(xiàn)在請同學們自己可以做了吧，證明相似，用的是一線三等角這個基本圖形，關(guān)鍵是第2 小題，更能體現(xiàn)這個基本圖形的優(yōu)勢，因為△AEF 是等腰三角形，其中的點E、F 都是動點，但是如果能想到只要滿足△ODE 是等腰了，那么△AEF 自然也一定是等腰三角形，這就容易多了，因為△ODE 中只有一個點E 是動點，研究起來就比較方便，現(xiàn)在我們就只要分三類情況來討論解決，畫出每一種狀態(tài)圖，請同學們試試吧。相信自己肯定行！

總而言之，利用基本圖形及其結(jié)論，能夠?qū)碗s的問題簡單化，幫助學生在較短的時間內(nèi)抓住問題的本質(zhì)，并可以防止解題中無關(guān)信息的干擾，提高我們的思維水平。