基于擾動觀測器的鋰電池荷電狀態估算方法
劉思佳,代高強,周 迅,孟令鋒,黃 勇
(四川長虹電器股份有限公司技術中心,四川成都610041)
鋰離子電池具有高能量密度、長周期壽命、低自放電率等性能特征,在備用電源、電動汽車、電網儲能等領域得到了廣泛應用。其電池管理系統的核心技術之一是對電池荷電狀態(SOC)的估算方法。最常用的荷電狀態估算方法為基于SOC定義的安時積分法[1],為了修正SOC誤差,該方法需結合開路電壓Uoc,由實驗數據建立Uoc-SOC關系曲線,來設定SOC初始值。由于安時積分法的開環特性,難以消除初始誤差,并在多次估算過程中易產生累積誤差。
另一類常用方法為基于模型的SOC估算方法,其特征包括電池等效電路模型與狀態估計算法兩部分,其狀態估計算法較多采用卡爾曼濾波(KF)類算法,其中擴展卡爾曼濾波(EKF)具有運算量相對較少的優勢[2-3]。相對于安時積分法,EKF 是一種閉環反饋算法,可消除初始賦值對估算結果的影響,并可消除因其引起的累計誤差。但該方法對電池模型參數的準確性要求較高,模型參數的偏差會直接影響估算結果。針對電池模型的時變性、非線性等特征進行優化與改進,以提升模擬實際電池的響應特性的精度,是基于模型的SOC估算方法的主要研究方向[3-4]。
本文提出一種基于擾動觀測器(DOB)的SOC估算方法,該方法根據擾動觀測器控制原理[5],建立了鋰電池電壓的擾動觀測模型,將充放電過程中電池數學模型存在的動態響應誤差作為擾動變量,通過電壓擾動觀測器得到補償電壓變量來實時修正狀態變量偏差,提高估算方法狀態估計模型的魯棒性,通過Matlab/Simlink 軟件仿真,驗證該方法的有效性。
1 基于電池模型的擾動觀測器設計
1.1 等效電路模型誤差分析
常用鋰電池的等效電路模型有Rint 模型、Thevenin 模型、DP 模型等[6-7],其中Thevenin 模型能較好地表征電池靜態與動態特性,其結構如圖1所示。圖中開路電壓為Uoc,歐姆內阻為Ro,極化電阻Rp與極化電容Cp的并聯電路代表極化電壓Up,電池端電壓為Ub,電池電流為Ib(放電時為正值)。由于是一階模型,其電池狀態方程只需4 個模型參數:放電時的歐姆內阻值Ro+、充電時的歐姆內阻值Ro?、極化內阻值Rp、時間常數τp=RpCp,在模型的精確度與復雜度之間具有較好的平衡,易于工程實現。基于該等效電路的數學模型為:
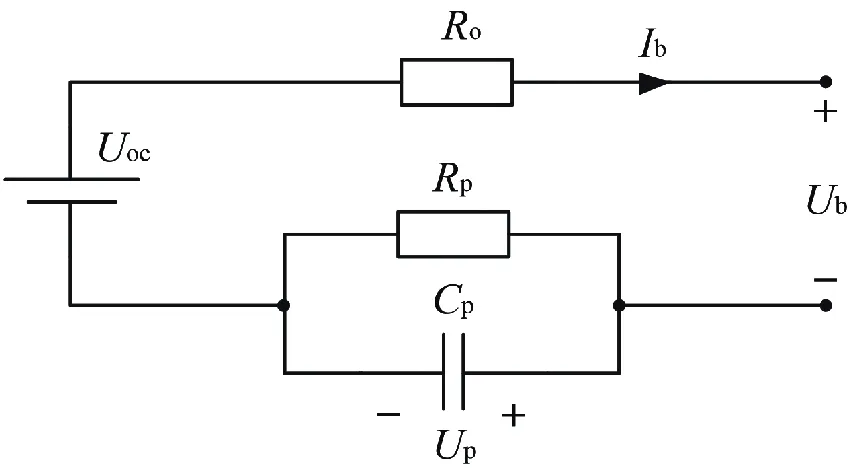
圖1 Thevenin電池模型
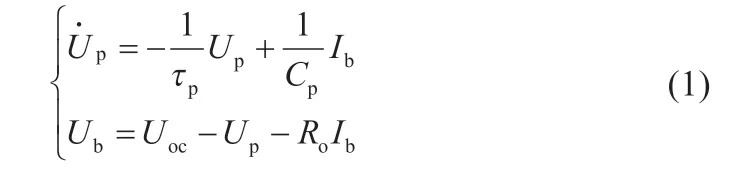
與二階RC 的DP 模型或更高階的電池模型相比,Thevenin 模型對極化電壓的模擬響應效果會存在較明顯的動態誤差。同時上述電池模型都沒有考慮鋰電池的滯后特性,例如磷酸鐵鋰電池的Uoc-SOC關系會表現出明顯的遲滯特性,即在放電與充電過程中,電池實際運行中Uoc-SOC對應關系與實驗數據得到的Uoc-SOC關系曲線存在不一致性[8-9]。可通過在模型增加滯后電壓變量的方式來補償這種動態誤差,但增加了模型復雜度及參數設定的難度[10]。本文通過建立電池電壓擾動觀測器模型,來實現對電壓動態誤差的實時修正,在不增加電池模型復雜度及模型參數個數的前提下提升對SOC估算的準確性。
1.2 鋰電池電壓擾動觀測器模型
擾動觀測器(DOB)系統原理圖見圖2。圖中P(s)與Pn(s)分別為具有時變性的單輸入單輸出實際系統與對應的標稱模型,兩者為同階并具有相同的相對階。信號d代表外部擾動變量,δ 為系統擾動變量的估計值,Q(s)為單位增益的低通濾波器。構建系統數學模型時,其標稱模型Pn(s)與實際系統P(s)在特定條件下會存在差異性,這種差異性與系統外部擾動d一樣,會降低數學模型的準確性。擾動觀測器將這種差異性視為系統內部擾動,其特點是同時對系統內部擾動與外部擾動造成的系統不確定性進行動態補償。當圖2 中系統信號頻率在濾波器Q(s)的低頻段時,系統的輸入輸出關系與系統的標稱模型Pn(s)保持一致,則原理上抵消了實際系統P(s)參數差異性與外部擾動變量d對系統模型準確性的影響[5]。
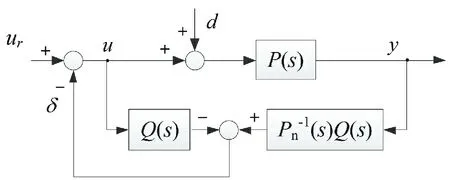
圖2 擾動觀測器系統原理圖
根據圖1 的電池模型結構,得到關于極化電壓Up的數學公式:
根據上述模型公式設計鋰電池電壓擾動觀測器模型如圖3所示,由公式(2)計算得到極化電壓的估算值Up。
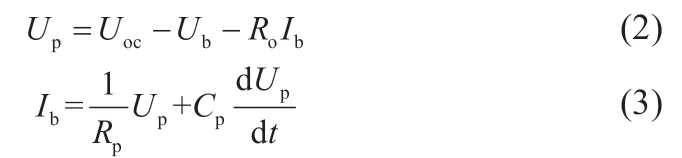
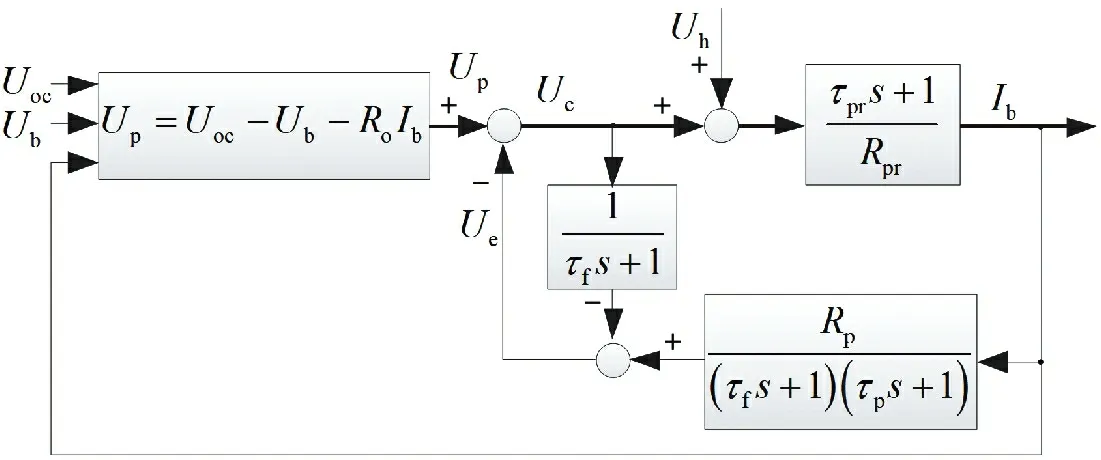
圖3 鋰電池電壓的擾動觀測器模型
根據公式(3),設定觀測器模型中實際系統P(s)為(τprs+1)/Rpr,其中Rpr與τpr分別為極化內阻與極化時間常數的實際值,具有時變性。標稱模型Pn(s)為(τps+1)/Rp,其中Rp與τp分別為應用于SOC估算的極化內阻與極化時間常數的模型參數。低通濾波器Q(s)采用一階濾波器,其時間常數為τf=1/(2πfc),fc為濾波器截止頻率。P(s)與Pn(s)之間的差異性定義為Thevenin 模型的極化電壓誤差,作為系統內部擾動量;將滯后電壓Uh作為電壓擾動觀測器模型的外部擾動量。內部擾動與外部擾動共同作用下的電壓擾動變量估計值為Ue。根據該電壓擾動觀測器模型,可得到離散化的電池動態補償電壓Uc:
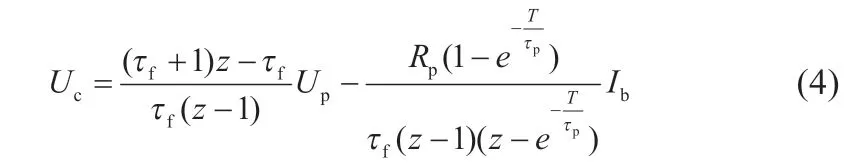
式中:T為系統采樣周期。
2 電池電壓擾動補償的SOC 估算方法
本文將鋰電池電壓擾動觀測器模型與EKF 算法相結合,設計了具有電池電壓擾動補償功能的SOC估算方法,用于實時修正滯后電壓及電池參數差異性對SOC估算的影響,其算法流程如圖4所示。

圖4 SOC估計算法流程圖
該方法屬于基于電池模型的SOC估算方法,對數學模型公式(1)進行離散化,并應用一階泰勒展開線性化后,得到SOC算法狀態估計模型所需的狀態方程與觀測方程為:
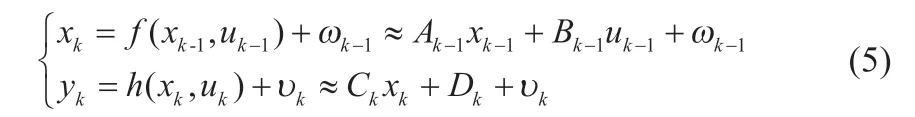
式中:x=[UpSOC]T,u=Ib,y=Ub;ωk-1為系統噪聲,其協方差為Qk-1;υk為測量噪聲,其協方差為Rk;系統矩陣定義為:
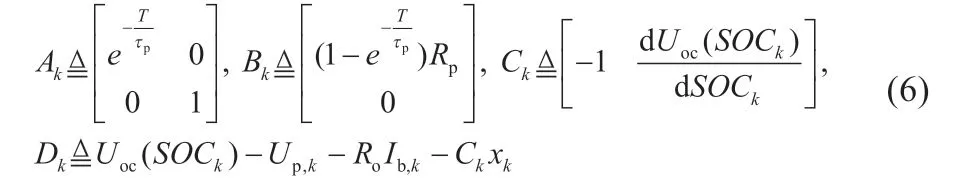
式中:Uoc(SOCk)為對實驗數據進行曲線擬合得到的SOC-Uoc關系式;T為系統采樣周期;Ro為歐姆內阻,放電時(Ib>0)電阻值為Ro
+,充電時(Ib<0)電阻值為。
該方法通過對狀態變量的初始化、預估、最優化修正的迭代計算,最終得到最接近真實值的SOC估算值。由EKF 算法更新其誤差協方差Pk計算卡爾曼增益Kk,用于計算本周期的狀態變量最優值。與常規EKF 算法相比較,該方法增加了補償電壓變量Uc,k-1,由圖3 的電池電壓擾動觀測器得到,將其替代電壓變量Up,k-1,代入狀態方程計算本周期的狀態預估值Uc,k,并將Uc,k代入觀測方程,用于計算更新本周期的觀測差值ek。其目的是在算法狀態估計模型與實際電池狀態之間出現偏差時,通過動態電壓補償的方式,降低上述不一致性造成的估算誤差。
3 仿真驗證與分析
本文以單體3.2 V/50 Ah 的磷酸鐵鋰電池為測試對象,采用HPPC 標準測試方法得到常溫下(25 ℃)的電池實驗數據。應用Matlab/Simulink 軟件搭建電池模型及SOC算法模型。搭建電池模型時,單體電池模塊的數據采用實驗數據,并根據磷酸鐵鋰電池的遲滯特性[9],在電池端增加了滯后電壓Uh,其與電池SOC的對應關系如圖5所示。SOC算法模型部分搭建了常規EKF 算法與本文的電池電壓擾動補償算法兩種系統模型,進行估算精度的對比仿真。SOC算法模型中,通過曲線擬合方式由實驗數據得到Uoc-SOC的關系曲線,采用Thevenin 模型構建電池狀態方程與觀測方程,其極化電壓變量存在一定響應誤差,且未設定滯后電壓變量,即算法中的電壓狀態變量存在極化與滯后兩種動態響應誤差。
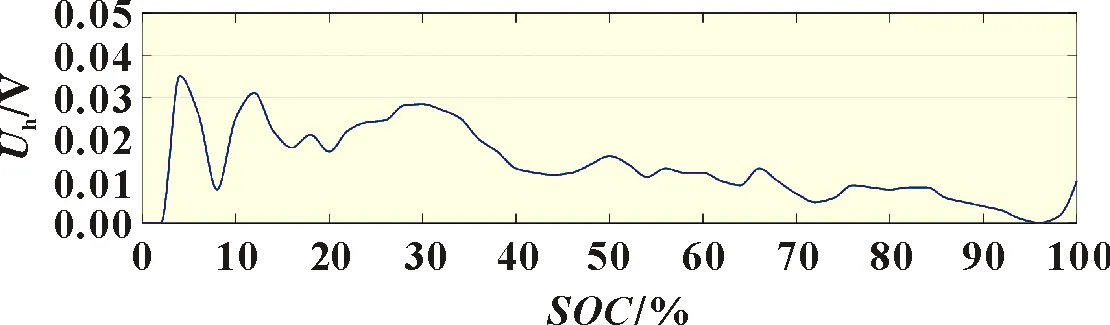
圖5 電池滯后電壓Uh與SOC對應關系圖
仿真計算時,充放電電流倍率設定為0.5C,電池電流、電壓采樣信號附加了功率譜密度為0.05 W/Hz 的白噪聲。放電測試將鋰電池荷電狀態由100%放電至0%,兩種估算方法的SOC初始值均設定為95%;充電測試將鋰電池荷電狀態由0%充電至100%,兩種估算方法的SOC初始值均設定為5%。
放電仿真對比結果如圖6所示,由圖中SOC估算曲線可以看到,兩種方法對估算初始值的依賴性都很低,均可快速修正初始值與SOC實際值之間5%的誤差,但到放電后期,由于鋰電池在低SOC區存在較明顯的滯后電壓(如圖5所示),導致常規EKF 方法的估算值出現了較大的動態誤差;本文方法則有效降低了滯后電壓對估算效果的影響,估算曲線更接近SOC實際值。充電仿真對比結果如圖7所示,充電初期由于滯后電壓影響,EKF 方法無法快速修正5%的初始誤差,且SOC估算曲線逐漸偏離實際值,直到充電后期滯后電壓下降,該方法的估算效果才有所改善;而本文方法在整個充電過程中,不受滯后電壓的影響,可快速修正初始誤差,并保持與實際值相近的估算效果。
圖5 持續峰值功率
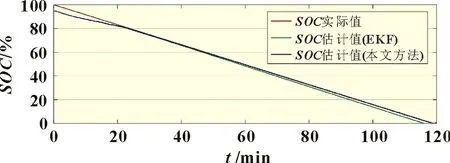
圖6 放電過程的SOC估算結果對比
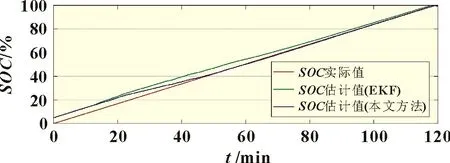
圖7 充電過程的SOC估算結果對比
圖8 為兩種方法在放電與充電狀態仿真測試的SOC估算誤差值對比。相對于極化電壓響應誤差,滯后電壓對SOC估算效果的影響較大。放電測試中兩種方法同步完成了對初始誤差的修正,不同的是EKF 的SOC估算誤差逐步增加,其最大絕對值為2.5%;本文方法則保持了穩定的估算效果,放電過程中SOC估算誤差的絕對值穩定在0.3%左右。充電測試中,初期由于滯后電壓的影響,兩種方法對初始誤差的修正速度都低于放電過程,EKF 的估算誤差增大至6.7%后緩慢降低,最終下降至0.9%;本文方法在充電初期的估算誤差值最大為5.2%并快速下降,優于EKF,充電中后期誤差絕對值已保持在0.2%左右。
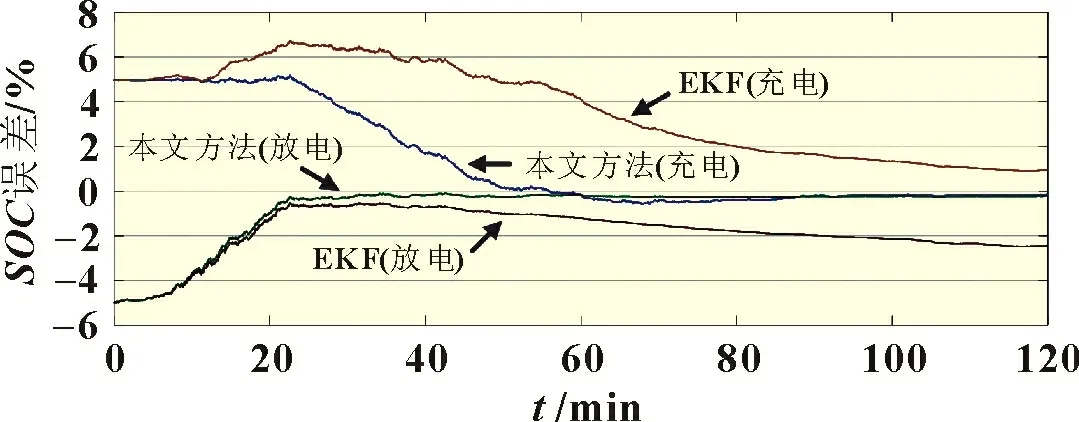
圖8 放電/充電過程中的SOC估算誤差值
綜合以上仿真結果,可以看出當SOC估算方法的數學模型參數與實際電池數據之間存在動態響應誤差時,本文的基于擾動觀測器的SOC估算方法,通過電壓擾動補償的方式降低了估算誤差,充放電過程中整體估算效果要優于常規EKF估算方法。
4 結論
本文通過建立鋰電池的電壓擾動觀測器模型,設計了與EKF 算法相結合的具有電池電壓擾動補償功能的SOC估算方法,采用Thevenin 電路模型構建算法狀態估計模型,通過電壓擾動觀測器的補償電壓變量實時修正模型響應誤差。通過仿真分析證明,與常規EKF 方法相比,該方法在放電與充電過程中均可提升對SOC估算的準確性。該方法暫未考慮溫度因素對估算效果的影響,后續工作中會根據溫度變化時模型參數特征進一步提升該方法。

