基于人工彈簧模型的周期結構帶隙計算方法研究1)

馮青松 楊 舟 郭文杰,2) 陸建飛 梁玉雄

*(華東交通大學鐵路環境振動與噪聲教育部工程研究中心,南昌 330013)

?(江蘇大學土木工程與力學學院,江蘇鎮江 212013)

引言

周期結構因其具有良好的彈性波衰減特性[1-2](帶隙特性),在結構振動與噪聲控制領域體現出了巨大的潛力.近年來,周期性結構中彈性波的波動特性研究發展迅速,從單一的周期性梁[3]、板結構[4-5]拓展到復雜的三維結構[6-7].與此同時,作為周期結構最為重要的特性,帶隙頻率的放大和調諧技術已成為當前研究的一個熱點,大量的學者立足于此,以梁板結構為基礎,將智能材料(如壓電材料[8-9]、磁流變材料[10]、功能梯度材料[11]等) 和彈簧-振子系統[12-15]引入周期結構中,以實現帶隙的主動調控和帶寬的增大,并取得了很好的效果.

在過去的幾十年里,學者們提出了大量的周期結構帶隙計算的數值和解析方法.有限元法[16-19]作為一種純數值方法,其在計算復雜周期結構帶隙方面表現出強大的能力.但是,有限元方法的精度依賴于離散單元的網格尺寸,高精度往往意味著很大的計算成本.且有限元法中構件耦合和端部邊界條件的處理過程比較繁瑣.后續也有部分學者針對復雜周期結構的帶隙計算,為提高傳統有限元法的計算效率,提出了一些新的數值方法,如波動有限元法[20-21],并將其迅速推廣到超材料桿[22]、多孔板[23]、周期性加筋殼[24]等結構的帶隙計算之中.但是無論從檢驗數值法的角度,還是從揭示復雜系統振動機理的角度,解析或半解析方法不可或缺.目前帶隙計算的常用解析方法主要有傳遞矩陣法[25-26]、平面波展開法[27-28]等.傳遞矩陣法對研究一維周期結構的帶隙特性非常方便高效,例如帶有周期彈簧支撐的軌道結構[29-30].對于一維結構,傳遞矩陣法是一種通用的方法,但用傳遞矩陣法難以處理多維以上的結構.平面波展開法是計算一維、二維和三維周期結構帶隙的傳統方法,但是由于該方法基于對微分方程組的直接求解,因此,在處理一些具有復雜邊界條件的周期性組合結構時存在一定的困難.此外,也有學者提出了一些新的周期結構帶隙計算方法,諸如譜動剛度法[31]、小波法[32]、漸進匹配展開法[33]等,這些方法雖各有特點,但處理一些復雜周期結構模型(如周期性組合結構)并不適用.因此,有必要發展分析復雜周期結構振動帶隙特性的解析或半解析方法.

能量法具有將求解微分方程邊值問題轉化為泛函極值問題的優點,這有利于復雜結構系統耦合問題的求解,因而傳統能量法(如Rayleigh-Ritz 法[34-35])被廣泛應用于分析一些復雜組合結構的自由振動問題[36-37],近年來也被引入周期結構帶隙計算中[38-39].但在利用傳統能量法計算周期結構帶隙時,存在如下問題:(1) 能量法需要基于Bloch 定理構造滿足周期性邊界的位移場形函數[40-41],從數學角度而言,形函數的周期性重構難度較大,而且不同形函數的構造方式不一定相同;(2)重構以后的位移場形函數包含波數,這會導致涉及形函數的結構的質量和剛度矩陣中含有波數,在計算帶隙時,結構的質量和剛度矩陣需隨著波數的變化進行反復計算,隨著結構質量和剛度矩陣維度的增大,或者掃描波數點數的增多,計算成本也會隨之增大.因此,對于能量法而言,以較低的計算成本對復雜周期結構的帶隙進行精確計算是一項具有挑戰性的工作.

鑒于此,本文對傳統能量法進行了改進,提出了一種利用人工彈簧[42-44]來模擬周期邊界條件的方法,將形函數與周期邊界條件分離,無需構造滿足周期邊界的形函數,這樣可解決傳統能量法中構造滿足周期邊界條件的形函數的困難問題;同時,利用人工彈簧模擬周期邊界條件,將周期邊界約束轉化為人工彈簧的彈性勢能,這樣只有包含波數的周期邊界彈性勢能矩陣需參與隨波數掃描的循環計算,其他矩陣只需計算一次,因而能提高傳統能量法計算帶隙的效率.此外,人工彈簧模型使用靈活、便捷,可進一步拓展到更為復雜的周期性組合結構的帶隙分析中.

1 人工彈簧模擬周期邊界的基本原理

1.1 問題陳述

以圖1 所示周期性薄板為例,對引言中提到的傳統能量法計算周期結構帶隙時存在的問題進行具體闡述.

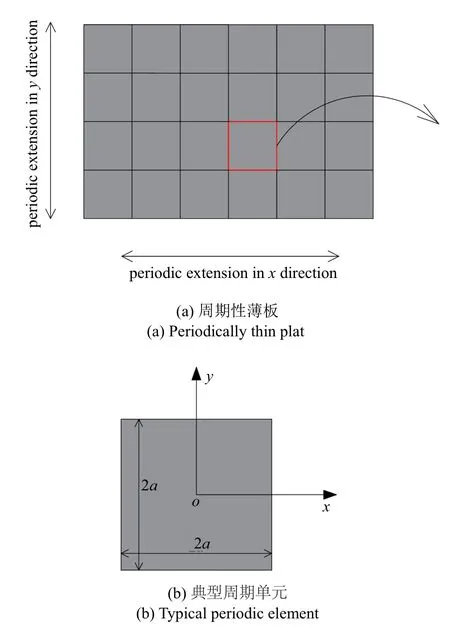
圖1 周期性薄板自由振動分析模型Fig.1 Vibration analysis model of a periodically thin plate with free boundary

對于圖1 所示的周期薄板結構,取出一個周期單元進行分析.根據Kirchhoff-Love 薄板理論,平面內位移u和v可以通過一階泰勒級數圍繞中面層展開,表示為平面外位移w,位移向量可以表示為

將式(1)中的橫向位移w表示為基函數ξi(x,y)和一個未知的權重系數di(t)的組合,即

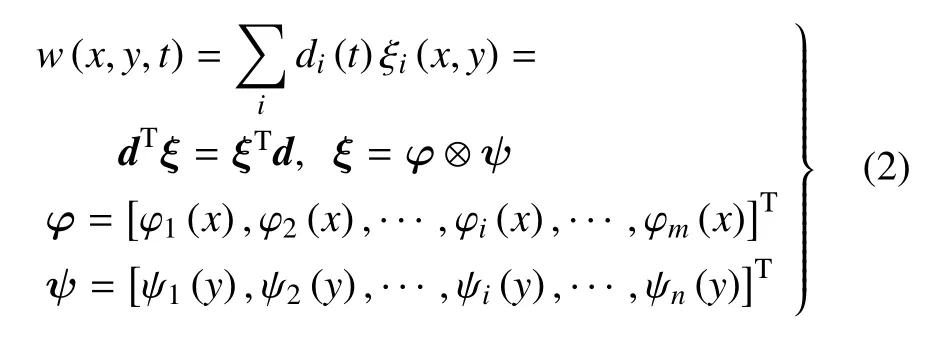
式中,符號?表示克羅內克積.

根據Bloch 定理,周期單元在x,y方向上的位移、轉角、彎矩和剪力需要滿足Bloch 周期性邊界條件,即

式中,kx,ky表示沿著x,y方向的波數.方程(3)～(6)要求式(2)中的形函數ξi(x,y)滿足Bloch-Floquet 周期性條件.從數學角度而言,形函數的重構過程具有相當大的難度,且不同的形函數構造方式不一定相同,這給利用傳統能量法求解周期結構振動帶隙問題帶來了困難.

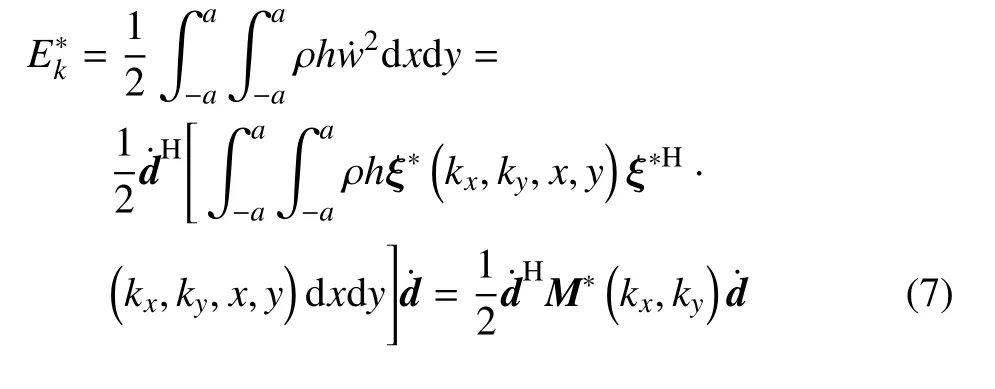
其中,ρ,h,ν 分別表示板的材料密度、板的厚度以及板材料泊松比;D=E*h3/[12(1-ν2)]表示板的抗彎剛度.由式(7)、式(8)可以得到周期單元的整體拉格朗日量

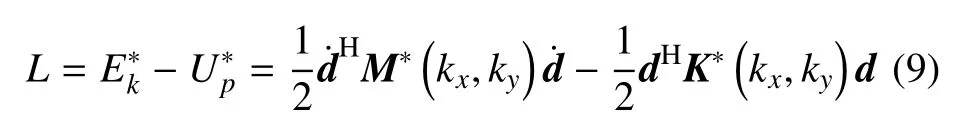
進一步地,定義未知的與時間相關向量d(t)=結合Eular-Lagrange 方程

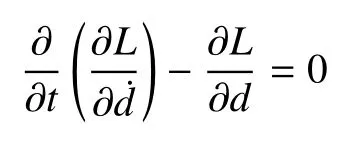
就能導出周期薄板結構的運動方程

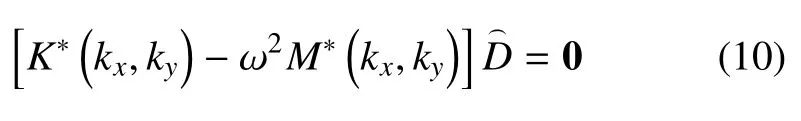
式(10) 是一個標準的特征值方程問題,在第一布里淵區kx×ky=[-π/a,π/a]×[-π/a,π/a]掃描波數,即能得到周期薄板結構彎曲振動的頻散曲線.值得注意的是,由于重構以后的形函數必然包含波數,這就導致利用位移形函數表征的結構動能表達式(7)和應變能表達式(8)中也含有波數,進而使得薄板結構運動方程(10)中的質量矩陣剛度矩陣同樣包含波數.因此,在掃描波數進行帶隙計算時,結構的質量和剛度矩陣需要隨著波數的變化進行循環計算,計算時間會隨著結構的質量和剛度矩陣維度以及掃描波數點數的增大而呈倍數增大,計算成本也會急劇增大.因此,如上所述,對于傳統能量法而言,以較低的計算成本對復雜周期結構的帶隙進行精確計算是一項具有挑戰性的工作.

1.2 人工彈簧模擬周期性邊界條件

嘗試將特殊的周期性邊界條件與位移形函數完全分離,即無需對形函數進行重新構造,用人工彈簧的形式來模擬周期性邊界條件.如圖2 所示,在周期單元的4 條邊界處定義線彈簧和轉角彈簧兩類彈簧,它的物理意義是在x和y兩個方向通過人工彈簧將上一周期單元的尾端與下一周期單元的首端相連.文獻[3]證明了,只需要位移和轉角滿足周期性條件,解即收斂于真實解.

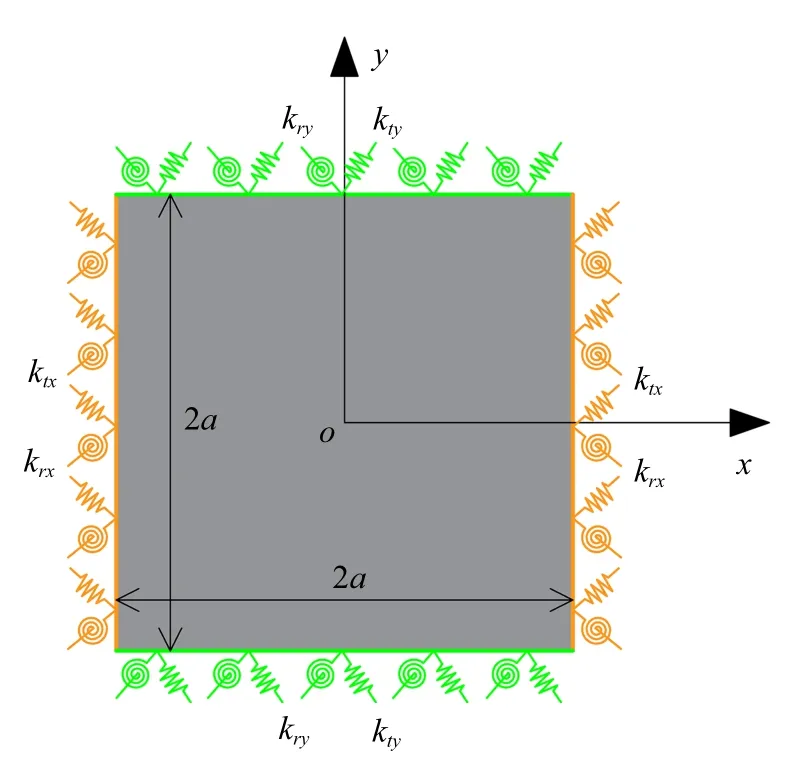
圖2 人工彈簧定義周期性邊界的分析示意圖Fig.2 Analysis schematic diagram of periodic boundary defined by artificial spring

以x方向為例,此時邊界勢能可以表示為

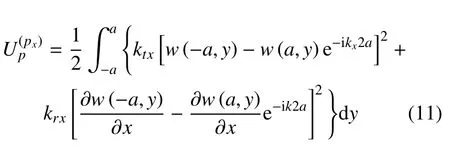
式中w(-a,y)-w(a,y)e-ikx2a,?w(-a,y)/(?x)-[?w(a,y)/(?x)]e-ik2a分別表示第一個周期首端與第二個周期首端的位移、轉角差值.同時,由式(3)、式(4)可知位移和轉角的差值趨于0,即

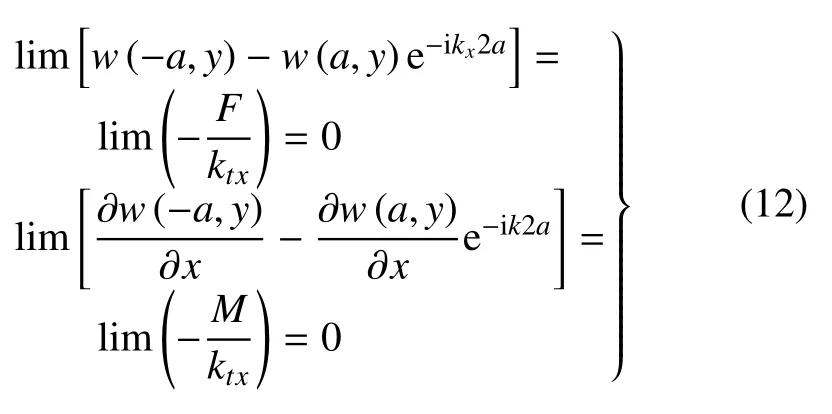
結構的剪力和彎矩都是一個有限值,因此式(12) 若要成立,則需要滿足limktx=∞,limktx=∞,同理考慮y方向的周期性邊界,式(11)改寫為

在式(13) 中,周期性邊界條件表示為包含波數在內的彈性勢能的形式,與位移形函數分離.此時,形函數ξi(x,y) 無需進行構造以滿足周期性邊界,周期單元的動能和應變能表示為

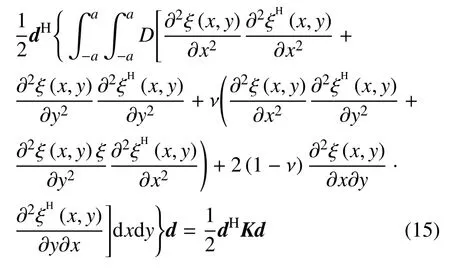
進一步地,周期單元的整體拉格朗日量表示為

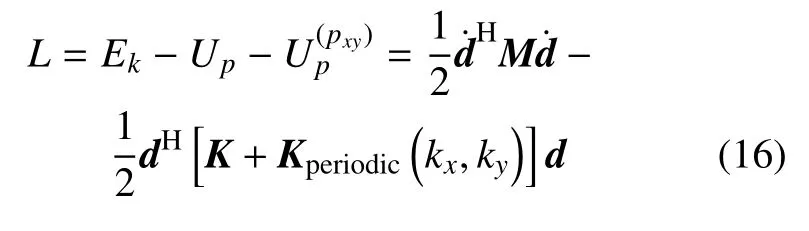
結合前述定義的與時間相關未知向量d(t)=以及Eular-Lagrange 方程

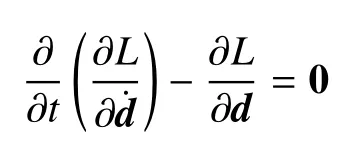
式(10)中周期薄板結構的運動方程改寫為

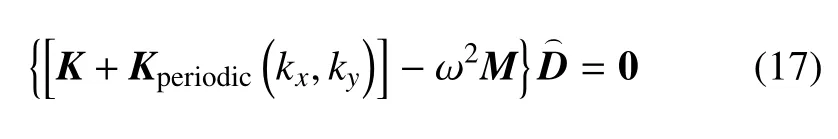
通過比較方程(14) 和(15) 與方程(7) 和(8) 可以發現,利用人工彈簧模擬周期性邊界,將位移形函數與周期性邊界條件分離,選取的形函數無需滿足周期性邊界,進而用形函數表征的結構動能和應變能表達式中沒有包含波數,同時通過對比最后的特征值方程(17) 和(10) 可以看出,僅有周期邊界勢能剛度矩陣中包含波數,質量與應變能剛度矩陣中都不包含波數,在掃描波數進行求解時,除了周期邊界彈性勢能矩陣參與波數掃描循環計算,其他的矩陣僅需計算一次,這將大幅度提高計算效率,進而降低計算成本.后續的算例驗證中,將進一步證明本文方法的準確性和效率性.

2 算例驗證:周期開口板彎曲振動帶隙計算

開口板廣泛應用于土木、船舶等結構中.開孔板的振動在能量傳遞中起著重要作用,但也與輻射噪聲對周圍環境的影響有直接關系.因此,本節以周期開口板為例,驗證人工彈簧模擬周期性邊界的準確性,同時說明該方法與傳統能量法相比,在計算效率上的優勢性.

2.1 位移形函數的選取及特征值方程求解

由于開口板出現了局部厚度突變,若選用改進傅里葉級數、切比雪夫級數等(適用于描述連續性較好的結構) 作為位移形函數可能需要多項級數來進行擬合以達到精度要求,進而降低計算效率.因此,本文選取具有局域化特性的高斯小波函數[45-46]為位移形函數,以確保能夠準確捕捉到厚度變化區域的波動特征,即對于式(2)定義

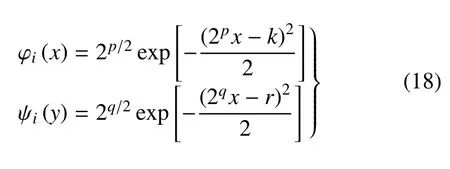
式中,p,q和k,r分別表示伸縮因子和平移因子.伸縮因子p,q控制著解的精度,采用越大的尺度因子使得形函數具有更高的分辨率,進而能更精確地模擬更高頻的波場,但同時要求更多的計算資源.平移因子k,r由伸縮因子p,q決定,其數量控制著式(18)中i的取值范圍,也就是形函數的個數和矩陣的維度.伸縮因子與平移因子的取值滿足

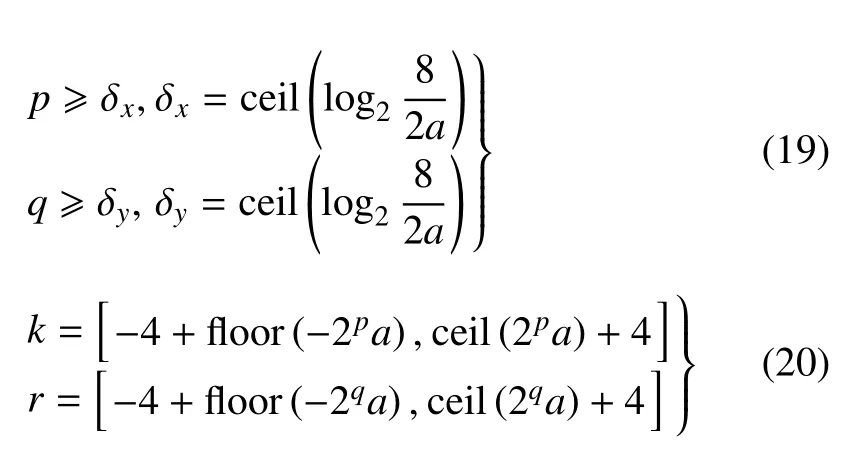
式中,ceil(*)表示最接近并大于*的整數,floor(*)表示最接近并小于*的整數.關于高斯小波函數的詳細介紹可以參考文獻[45-46].定義一個厚度函數h(x,y)滿足

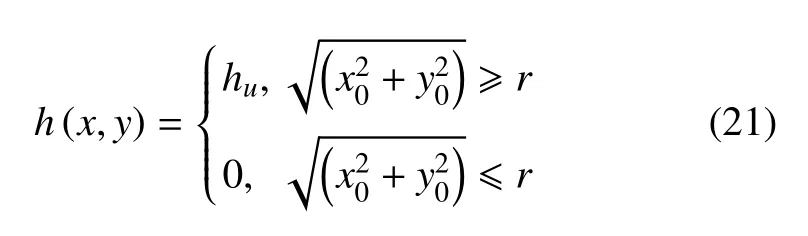
其中,x0和y0分別表示圖3 所示開口板坐標系內任意一點的橫坐標和縱坐標;hu表示板的標準厚度;r表示圓形開口半徑.利用式(21) 中的h(x,y) 替換式(14)、式(15) 中的h,掃描波數求解特征值方程(17)即能得到周期開口板彎曲振動的頻散曲線.

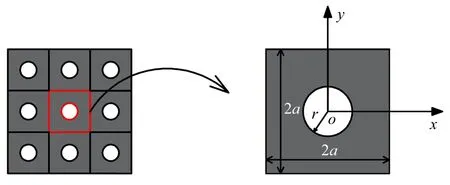
圖3 周期開口板分析模型Fig.3 Analysis model of periodic plate with opening

2.2 準確性分析

2.2.1 人工彈簧剛度取值收斂性分析

由前述分析可知,當用人工彈簧模擬周期邊界條件時,人工彈簧剛度需要取為無窮,但在實際計算過程中需要用一個較大的值來代替,因此位移約束彈簧和轉角約束彈簧剛度的取值在很大程度上影響了計算結果的準確性,需要對人工彈簧剛度取值進行收斂性分析,找到解收斂時的彈簧剛度取值,從而能夠準確替代人工彈簧剛度取無窮這一情況.板的長度和寬度都為0.12 m,板的均質厚度取0.001 m,圓形開口半徑為0.036 m,選取鋼材料為板的材料,密度為7800 kg/m3,彈性模量為210 GPa,泊松比為0.3.從頻散曲線中隨機選取3 條曲線波數位于kx=ky=π/a處的頻率為研究對象,其結果如圖4 所示.

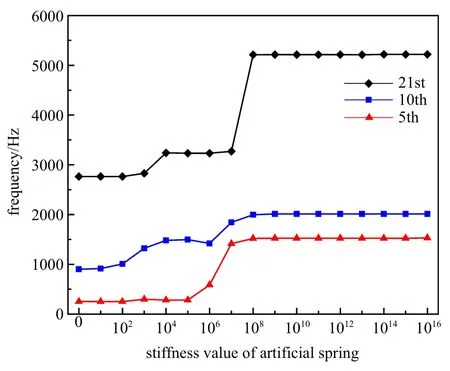
圖4 人工彈簧剛度取值收斂性分析Fig.4 Convergence analysis of stiffness of artificial spring

由圖4 可以看出,當彈簧剛度系數數值大于1010時,得到的波模態頻率值已經趨于穩定,基本不再變化,認為結果已收斂于周期性邊界.表明當利用人工彈簧周期性邊界條件時,實際計算中只要將剛度系數的數值取為ktx=kty=1010N/m2,krx=kry=1010N/rad 時即可得到收斂的解.

2.2.2 頻散特性對比分析

圖5 給出了本文方法計算得到的周期開口板彎曲振動頻散曲線,為了對比,同時給出了利用文獻[41] 中重構位移形函數的方法計算得到的結果.其中兩種方法采用的形函數均為高斯函數,板的幾何和材料參數一致,伸縮因子、平移因子取值以及掃描波數均保持一致.

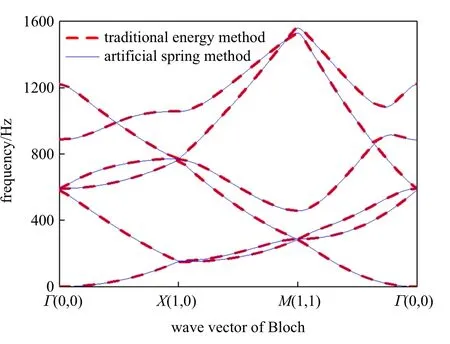
圖5 周期開口板彎曲振動頻散曲線Fig.5 Dispersion curve of bending vibration of periodic plate with opening

由圖5 可以看出,兩種方法計算得到的結果基本一致,即0～1500 Hz 范圍內,圖3 所示的這種周期開口板結構沒有產生完全帶隙和方向帶隙,進一步說明了利用人工彈簧模擬周期邊界的準確性.

2.3 效率對比分析

2.3.1 掃描波數的影響

掃描波數決定了頻散曲線上點的個數,越大的掃描波數能夠得到更為平滑的頻散曲線.本節分析了不同掃描波數下,兩種方法計算頻散曲線的時效性,將對比結果列于表1.分析中保持伸縮因子為6不變.

由表1 可以看出,當掃描波數為30 時,本文方法求解僅需要4.5 s,而傳統能量法需要27.5 s,約為本文方法的6.1 倍;隨著掃描波數的增大,時間倍數越來越大,本文方法效率性體現得更加明顯,當掃描波數為300 時,傳統能量法需要268.2 s,約為本文方法的21.8 倍.這是因為傳統能量法需要對位移場形函數進行重構以滿足周期性邊界條件,這就導致結構的動能和應變能矩陣中都含有波數,每掃描一次波數,結構的動能和應變能矩陣都要計算一次,隨著掃描波數的增大,動能和應變能矩陣的計算次數也隨之增大,這極大地延長了求解時間.而本文提出的利用人工彈簧模擬周期性邊界條件的方法,通過將周期性約束條件轉變為彈性勢能,僅在有邊界彈性勢能矩陣中包含波數,結構的動能和應變能矩陣只需要計算一次,只有彈性勢能矩陣參與掃描波數的循環計算,這就使得求解時間大大縮短.

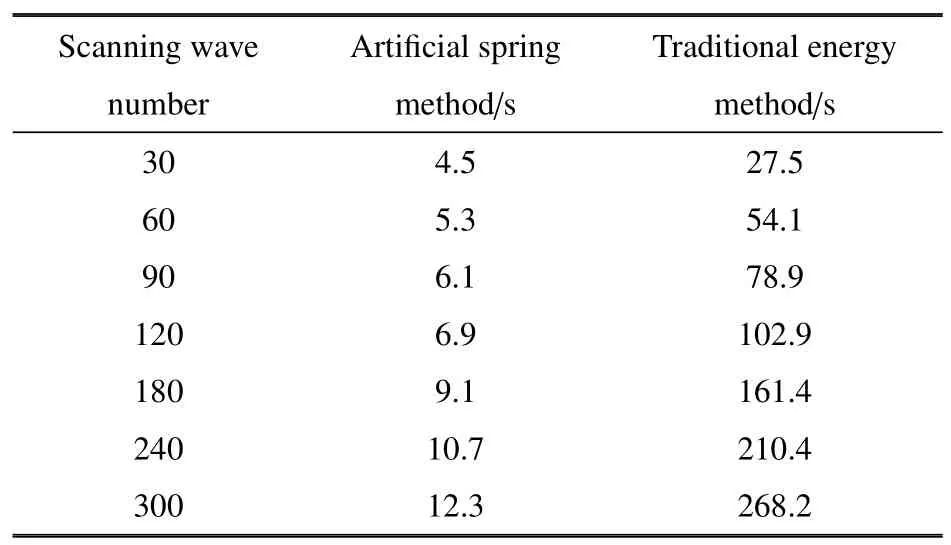
表1 不同掃描波數下計算時效對比Table 1 Comparison of calculation time under different scanning wave number

2.3.2 矩陣維度的影響

前文中提到,伸縮因子控制著解的精度,采用越大的尺度因子使形函數具有更高的分辨率,但同時要求更多的計算資源.平移因子由伸縮因子決定,其數量控制著形函數的個數和矩陣的維度.本節分析了不同伸縮因子(矩陣維度) 條件下,兩種方法計算頻散曲線的時效性,將對比結果列于表2.分析中保持掃描波數為100 不變.

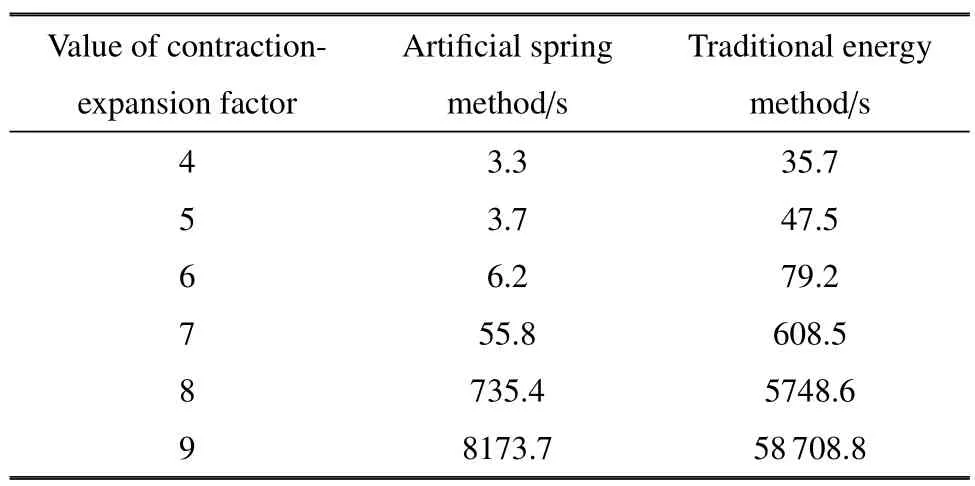
表2 不同矩陣維度下計算時效對比Table 2 Comparison of computational effectiveness under different matrix dimensions

傳統能量法需要對位移場形函數進行重構以滿足周期性邊界條件,這就導致結構的動能和應變能矩陣中都含有波數,結構的動能和應變能矩陣需要隨著波數變化進行反復計算,隨著伸縮因子取值的增大,平移因子的取值范圍也隨之增大,動能和應變能矩陣的維度也隨之增大,這就導致每次循環計算動能和應變能矩陣的時間增大.

本文提出的利用人工彈簧定義周期性邊界的方法,僅在邊界彈性勢能矩陣中包含波數,結構的動能和應變能矩陣不需要參與波數循環,只需要計算一次,僅有邊界彈性勢能矩陣參與隨波數的循環計算.雖然伸縮因子的增大也導致了邊界彈性勢能矩陣維度的增大,但其計算量遠小于增大結構的動能和應變能矩陣維度的計算量,這就使得隨著伸縮因子的增大,本文提出的人工彈簧定義周期邊界的方法求解時間增長量遠小于傳統能量法:由表2 可以看出,當伸縮因子由4 增大到5 時,本文方法求解時間由3.3 s 延長到3.7 s,求解時間延長0.4 s;而傳統能量法求解時間由35.7 s 延長到47.5 s,求解時間延長11.8 s,約為本文方法的29.5 倍.同時,在編程計算中,隨著矩陣維度的增大,不僅結構的動能和應變能計算時間增大,最后特征值求解的時間也隨之增大,因此在表3 中,當伸縮因子由7 增大到8 時,本文方法求解時間從55.8 s 延長到735.4 s,延長了679.6 s.但相比于傳統能量法,優勢還是很明顯,對傳統能量法,伸縮因子由7 增大到8 時,求解時間從608.5 s 延長到5748.6 s,延長了5140.1 s.因此,相較于傳統能量法,隨著模型復雜程度的增加以及分析精度要求的提高,結構的質量剛度矩陣維度以及掃描波數點數隨之增大,本文提出的用人工彈簧模擬周期性邊界的方法在計算效率上的優勢也會越來越明顯.

3 周期組合結構振動帶隙計算

在鐵路工程、土木工程、機械工程等領域,組合結構是一種常見的結構類型.這類結構通常也具有周期性,研究這類組合結構的帶隙特性,能夠更全面地理解彈性波在結構中的傳播特性,從而更好地指導其減振降噪設計.在簡化建模過程中,由于組合結構的復雜性,可能是由梁-板耦合、多塊板耦合甚至是板-圓柱殼耦合等,這就導致在利用位移形函數進行結構動能和勢能的表征時,形成的質量和剛度矩陣維度很大.針對這種大維度矩陣問題,若通過重構滿足周期性邊界的位移形函數的方法來進行帶隙計算,將會面臨相當大的計算成本.因此,本節以我國CRSTIII 型無砟軌道結構為例,采用人工彈簧定義周期性邊界的方法,計算了周期性組合結構彎曲振動的帶隙,并與有限元結果進行了比較.

3.1 模型簡化

建立圖6 所示的由鋼軌、扣件、軌道板和CA 砂漿層組成的無限周期結構.扣件與CA 砂漿層簡化為彈簧單元;為同時考慮鋼軌和軌道板的彎曲和剪切性質,鋼軌簡化為Timoshenko 梁單元,軌道板簡化為Mindlin 板單元,鋼軌選用60 kg/m 鋼軌.本文基于鋼軌和軌道板的周期性與對稱性(假設結構對稱及載荷形式對稱),可以取一個周期下結構的一半進行建模,模型如圖7 所示.l為單個軌道板的長度,相鄰軌道板之間是不連續的,s0為軌道板間縫隙的大小.l+s0為鋼軌周期,其小周期為l0,且l0=(l+s0)/9.c為軌道板寬度的一半,y*為鋼軌距軌道板外側邊緣的寬度.圖中分別針對鋼軌和軌道板建立了兩個笛卡爾坐標系x′O′y′和xOy.

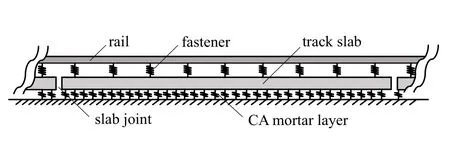
圖6 CRTSIII 無砟軌道結構縱斷面示意圖Fig.6 Schematic diagram of the longitudinal section of the CRTSIII track structure

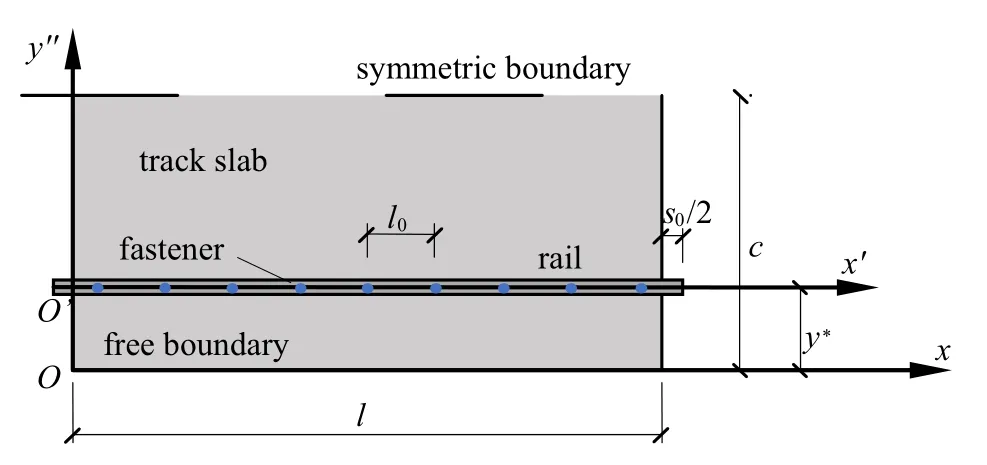
圖7 CRTSIII 型無砟軌道結構典型單元示意圖Fig.7 Schematic diagram of CRTSIII track structure of a cell

3.2 運動方程的建立

鋼軌和軌道板的位移場可以分別寫為與式(2)類似的形式,即

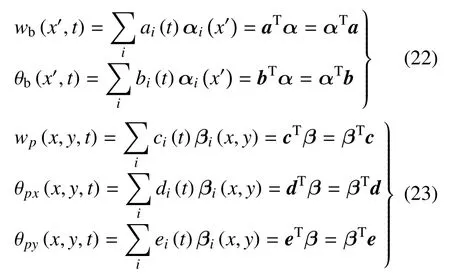
其中,wb(x′,t) 和θb(x′,t) 分別表示鋼軌的垂向位移和截面轉角函數;wp(x,y,t),θpx(x,y,t),θpy(x,y,t) 分別表示軌道板彎曲振動位移、沿x方向轉角以及沿y方向轉角函數.鋼軌與軌道板位移場形函數都采用第2 節提到的高斯函數.

3.2.1 鋼軌的動能和應變能

分析中鋼軌考慮為Timoshenko 梁,因此其動能包含了平動動能和轉動動能,應變能包含了彎曲應變能和剪切應變能,即

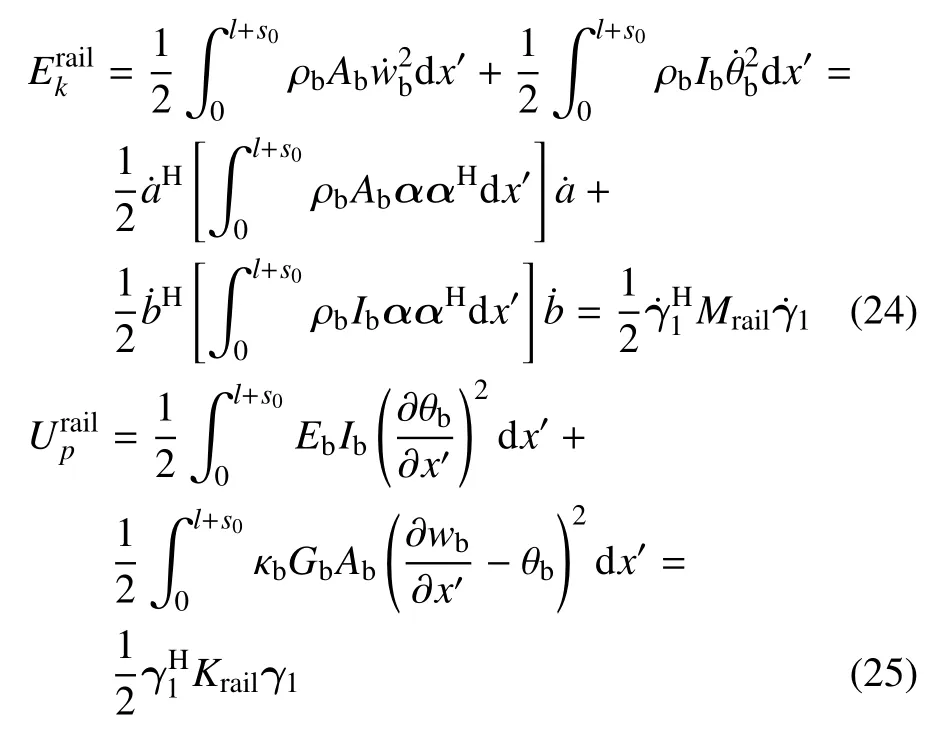
3.2.2 軌道板的動能和應變能

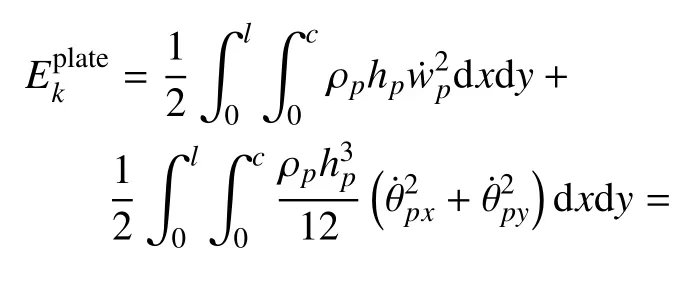
3.2.3 扣件彈性勢能與軌道板下彈性地基勢能

模型中9 個扣件的總彈性勢能可表示為

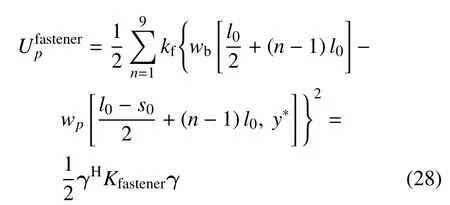
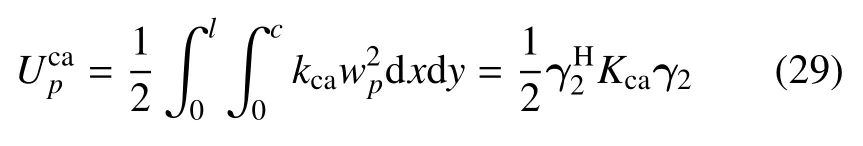
3.2.4 對稱邊界及周期性邊界條件的定義

圖7 中xOy坐標系y=c處邊界為正對稱邊界,可認為板邊界上轉角為0,位移自由,利用人工彈簧模擬正對稱邊界條件,線彈簧和轉角彈簧剛度分別表示為kts和krs,剛度取值參考文獻[43].在x′O′y坐標系上x′=0 和x′=l+s0處為Floquet 周期性邊界,由于CRSTIII 型軌道板結構是不連續的,相鄰軌道板之間存在板縫,因此軌道板沒有Floquet 周期性邊界.整體結構的邊界勢能可表示為

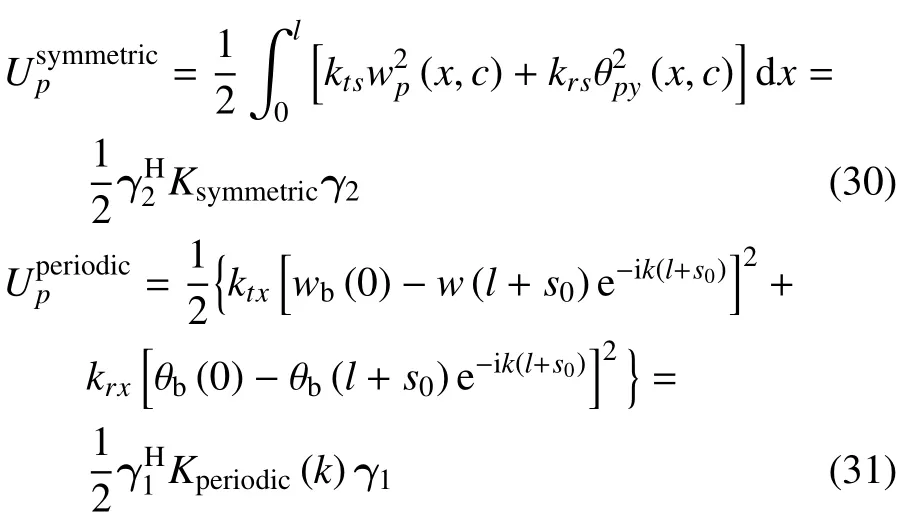
3.2.5 單個周期的拉格朗日能量泛函

單個周期結構的總動能和總勢能可表示為

單個周期結構整體的拉格朗日量可寫為

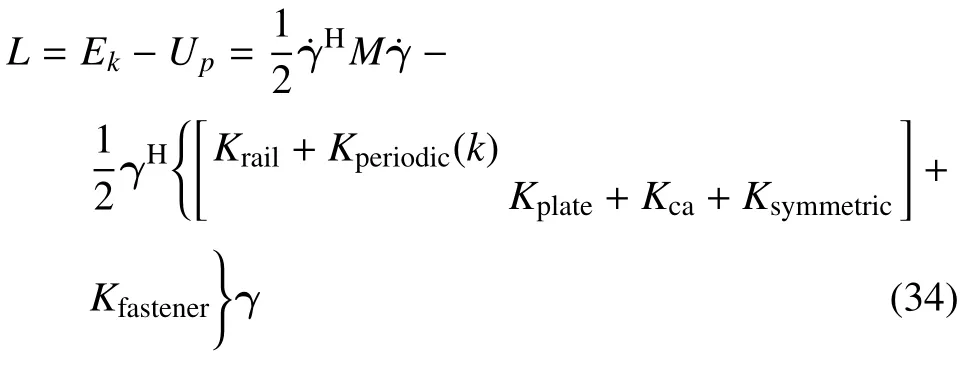
結合前文中提到的歐拉-拉格朗日方程,可以將式(34)轉化為標準特征值方程問題,即

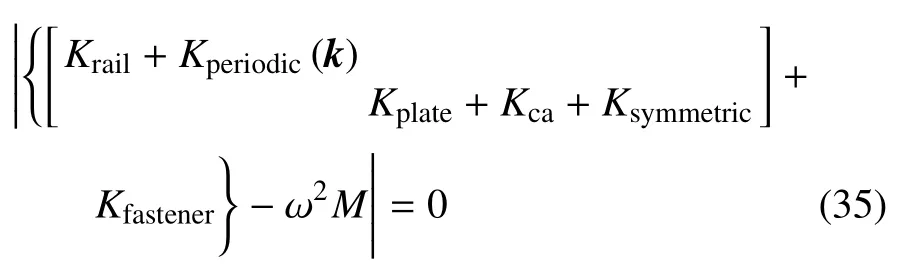
在第一布里淵區掃描波矢k=[-π/(l+s0),π/(l+s0)],求解特征值方程(35)就能得到周期梁-板組合結構彎曲振動的頻散曲線.

3.3 算例分析

為了進一步驗證本文方法的正確性,建立了單個周期CRSTIII 型無砟軌道結構有限元模型,如圖8所示.鋼軌與軌道板均考慮為實體單元,扣件與CA砂漿層分別簡化為點彈簧和均布彈簧,其中,鋼軌與軌道板通過扣件彈簧連接,軌道板與基礎通過CA 砂漿均布彈簧連接.軌道板的內邊界添加正對稱邊界條件,在鋼軌兩端添加Floquet 周期性邊界條件,其余邊界為自由邊界.鋼軌、軌道板的幾何和材料參數以及扣件剛度、CA 砂漿均布剛度取值與上述半解析模型一致,鋼軌密度ρb=7850 kg/m3,截面積Ab=77.45 cm2,截面慣性比Ib=3217 cm4,彈性模量Eb=210 GPa,泊松比νb=0.3;軌道比密度ρp=2300 kg/m3,半寬度C=1.25 m,長度l=5.6 m,厚度h=0.21 m,彈性模量Ep=25 GPa,泊松比νb=0.2;軌道板間縫系S0=0.07 m,軌道與FSB 間距y*=0.492 2 m,垂直連接鋼度kf=7.2×107N/m,CA砂漿層的均勻支撐鋼度kca=1.723×108N/m3.選用多物理場仿真軟件Comsol Multiphysics 中的固體力學模塊進行求解,通過設置掃描波數求解得到了周期性無砟軌道結構的振動模態,從中挑選出垂向振動模態進行繪制即能得到垂向振動頻散曲線.0～1500 Hz范圍內,CRSTIII 型無砟軌道結構垂向振動產生了四階帶隙,圖9 給出了兩種方法計算結果對比.

圖8 CRTSIII 無砟軌道結構典型單元有限元模型Fig.8 FEM model of typical cell of CRTSIII track structure

圖9 CRTSIII 型無砟軌道結構垂向振動頻散曲線Fig.9 Vertical vibration dispersion curve of CRTSIII track structure

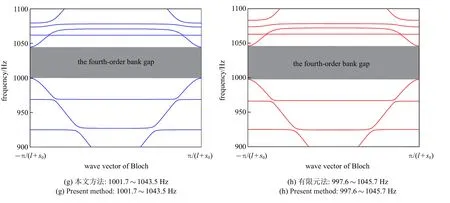
圖9 CRTSIII 型無砟軌道結構垂向振動頻散曲線(續)Fig.9 Vertical vibration dispersion curve of CRTSIII track structure(continued)

由圖9 可以看出,利用人工彈簧定義周期性邊界這種方法進行帶隙計算與有限元計算結果吻合度很好,再次證明了該方法的準確性.目前,針對此類復雜的周期性組合結構帶隙計算問題,主要是通過商業有限元軟件來實現.其中僅有Comsol 等少數有限元軟件可通過直接設置Floquet 周期性邊界并掃描波矢來實現帶隙計算.然而由于這類商業軟件目前計算模塊尚未完善,以Comsol 為例,對于圖6 所示的無砟軌道結構(梁-板組合結構)需要采用實體單元建模,計算量較大.利用人工彈簧模擬周期性邊界,除周期邊界處人工彈簧彈性勢能矩陣需隨波數變化而重復計算,其他矩陣均只需計算一次,可以解決計算量大的問題.

4 結論

本文基于能量法的基本框架,對傳統能量法進行了改進,提出了利用人工彈簧模擬周期性邊界條件的方法,實現了周期性邊界條件與位移形函數的分離.首先以周期開口板為例,驗證了本文方法的準確性,并與傳統能量法比較了計算效率;然后,針對周期性組合結構,以我國CRTSIII 型無砟軌道結構為例,分析了其垂向振動帶隙特性,并與有限元法進行了比較.通過本文的研究,可得如下結論:

(1)與傳統能量法以及有限元法的對比結果表明了本文方法具有很好的準確性.同時,相較于傳統能量法,利用人工彈簧模擬周期性邊界條件,無需構造滿足周期邊界的位移形函數,進一步實現了周期邊界與位移形函數的分離,成功解決了傳統能量法中構造滿足周期性邊界條件形函數的困難問題,提高了能量法的適用性.

(2)與傳統能量法相比,利用人工彈簧模擬周期邊界,除周期邊界處彈性勢能矩陣需隨波數變化而重復計算,其他矩陣均只需計算一次,這極大地提高了計算效率,實現了以較低的計算成本對復雜周期結構的帶隙進行精確計算.隨著模型復雜程度的增加以及分析精度要求的提高,結構質量、剛度矩陣的維度以及掃描波數點數也隨之增多,本文方法在計算效率上的優勢會更加明顯.