考慮界面力學性能的組件及結構的協同優化1)

馬 晶 趙明宣 王浩淼 劉 湃,2) 亢 戰

*(大連理工大學工業裝備結構分析國家重點實驗室,遼寧大連 116024)

?(上海宇航系統工程研究所,上海 201109)

引言

自20 世紀90 年代Bends?e 和Kikuchi[1]基于數值均勻化的拓撲優化方法提出以來,結構拓撲優化技術經歷了近30 年的快速發展,形成了較為成熟的理論體系,并被廣泛應用于航空、航天[2-3]、汽車[4]等各領域結構的輕量化[5]、多功能材料[6]等性能設計.在概念設計階段,結構拓撲優化技術在滿足多種設計約束的前提下,同時優化結構的形狀及拓撲以實現特定的優化目標.目前,被廣泛采用的拓撲優化方法主要包括變密度法[7](solid isotropic material with penalization,SIMP)、漸進結構優化法[8-9]及水平集方法[10-13],并發展出為各種具體的理論[14]和方法[15].其中,水平集方法基于隱式邊界描述,便于處理結構邊界的演化、融合,并能夠提供清晰的結構邊界描述.

在工程領域,包含嵌入式組件的結構較為常見,如衛星支架與導航定位等功能性組件.通常,此類包含嵌入式組件的結構需要應用在空間緊俏的狹小空間(如航天工程[16-17](如圖1 所示),微機電系統(micro-electro-mechanical systems,MEMS)以及汽車工程等),因而此類結構也常將部分功能性組件用于結構承載.

圖1 典型的飛行器多組件結構系統[17]Fig.1 Typical aircraft multi-component structure system[17]

針對這類結構,功能性組件與支撐材料連接界面的失效,會導致結構的剛度下降甚至完全喪失承載力.因而,考慮連接界面的力學性能對多組件結構進行設計十分必要.此外,為實現多組件結構的最優性能,需同時對支撐材料的分布及功能性組件的形狀及布局進行設計,并考慮組件最小距離控制等[16,18]設計約束避免組件間(如電磁等)功能的相互干涉.

目前,針對多材料及多組件結構設計,學者們提出了多種拓撲優化方法:Bends?e 和Sigmund[19]提出基于變密度法的多相材料插值模型;Wang 等[10]提出color level set 方法,在水平集法框架下采用m個水平集函數描述2m相材料的分布;Wang 等[20]提出多材料水平集方法,利用m個水平集函數描述m+1 相材料的分布,有效避免了設計域內因多個水平集函數相交而產生的冗余區域.張衛紅等[16-18]對多組件結構優化設計進行了一系列系統的研究,提出了基于有限圓形近似組件邊界位置的多組件距離控制約束及多組件結構拓撲優化方法;此外還有學者對嵌入孔洞的布局優化[21]進行了研究.然而,上述多材料及多組件設計方法,并未考慮材料連接界面可能發生的張開及失效.由于結構拓撲隨優化迭代實時演化,如何在優化過程中實時追蹤連接界面位置,準確描述界面的張開及失效成為了學者們關注的熱點問題之一.Lawry 等[22]針對material anchor 這一特殊雙材料結構,考慮材料界面的滑動摩擦接觸,對其剛度進行設計,并將此工作擴展到大變形[23]等現象;劉湃等[24-26]基于內聚力模型,結合擴展有限元方法在固定網格下提出考慮多材料及包含固定形狀組件結構連接界面力學性能的拓撲優化方法,考慮了界面可能發生的張開與失效,并以剛度為目標對結構進行設計.此外,考慮梯度界面的雙材料結構優化[27],考慮脆性材料界面的抗斷裂結構拓撲[28]和復合材料[29]結構優化,以及以接觸面分布力均勻化[30]為目標的結構拓撲優化等研究都探索了優化迭代時材料界面模型對最終設計的影響.

盡管作者在之前的工作[25]中對考慮連接界面力學性能的多組件結構拓撲優化進行了研究,但所考慮的內嵌組件形狀固定不變,這直接導致組件與支撐結構之間連接界面的形狀受限于給定組件的幾何形狀.然而,當考慮連接界面張開時,結構的性能不僅依賴于多組件的布局及支撐結構的拓撲,還顯著依賴于連接界面的形狀.因而,本文考慮連接界面力學性能,對形狀可變的多組件與支撐結構拓撲的協同優化進行研究,采用超橢圓描述可變組件,顯著擴展了設計空間,能夠描述更為復雜的連接界面形狀.本文針對包含多個內嵌組件的結構,考慮組件與支撐材料連接界面的力學性能,同時優化組件的形狀、空間布局及支撐結構的拓撲,以實現結構的最優剛度設計(見圖2).首先,采用超橢圓模型參數化組件的形狀及布局(如空間位置、旋轉角度等),并同時構造其水平集函數表達;進而,在固定網格下,以內聚力模型作為連接界面本構,結合水平集描述及擴展有限元方法,準確分析隨優化迭代不斷演化的連接界面的張開位移;進一步,在水平集方法框架下建立以剛度為目標的拓撲優化列式并推導解析的靈敏度表達,基于數學規劃算法[31](method of moving asymptote,MMA)求解優化問題.

圖2 包含嵌入組件的結構Fig.2 Structure with two embedded components

1 考慮界面力學性能的多組件結構分析

1.1 基于超橢圓描述的內嵌組件及其水平集函數構造

本文基于超橢圓模型參數化形狀可變組件的形狀及空間布局.超橢圓定義式為(|x/a|η+|y/b|η)=1,其中a,b分別為超橢圓的長軸、短軸,η 為超橢圓的階次,且a,b,η ＞0.超橢圓上的點坐標(x,y)可由以t為參數的參數方程表達

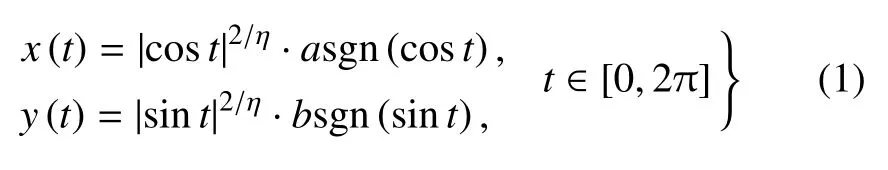
超橢圓模型可以描述從菱形到矩形的連續形狀變化.如圖3 所示,不同超橢圓階次η 控制了超橢圓的形狀:η=2 時為橢圓,η →∞時為矩形.為保證組件邊界的光滑性,避免可能出現的應力集中,本文限制參數η ∈[2,6].

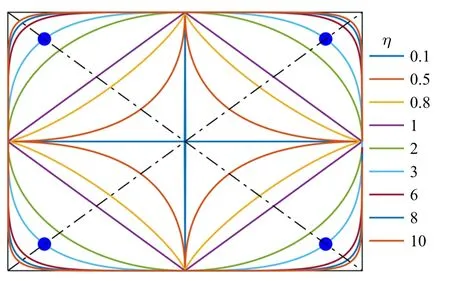
圖3 參數η 取不同值時超橢圓的形狀Fig.3 Superellipse with different parameter η values

超橢圓與坐標軸的交點為(±a,0),(0,±b),其頂點為(±sa,±sb),是從圓點出發到矩形4 個頂點的連線與超橢圓的交點(圖3 中的圓點),其中s=2-1/η.超橢圓的面積可以通過Beta 函數計算

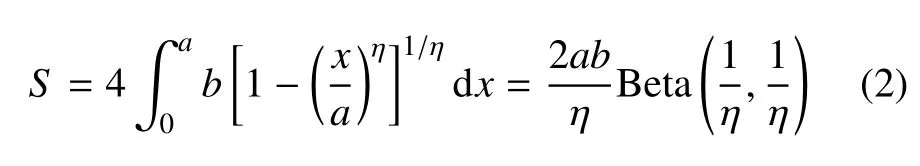
基于超橢圓的顯式參數表達,可構造其水平集函數為φ(γ)=-(|x′/a|η+|y′/b|η)+1,其中x′,y′為局部坐標,可由組件的中心坐標和角度(如圖4 所示) 變換得到

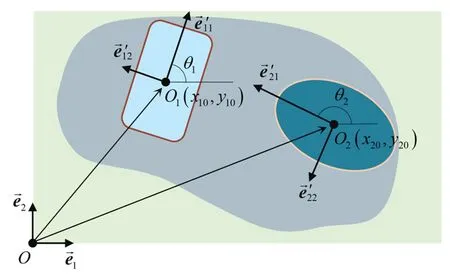
圖4 內嵌組件局部和整體坐標Fig.4 Local and global coordinate systems of the components

超橢圓組件的參數γ包括長短軸a,b以及旋轉角度θ,以及組件的中心坐標(x0,y0).圖5 給出了由參數γ構建的組件水平集函數.

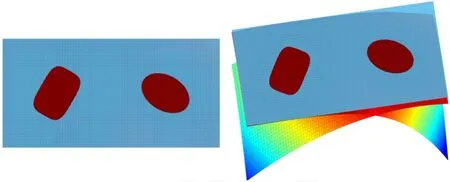
圖5 超橢圓組件的水平集函數Fig.5 Level set functions of superellipse components

1.2 結構拓撲及連接界面的水平集描述

本文中組件和支撐結構使用不同材料.本文采用多材料插值模型[20,25]描述設計域中內嵌組件,支撐材料的材料屬性,并描述其連接界面位置.對于包含M個內嵌組件的結構,需要M+1 個水平集函數對其進行描述,其中φm(m=1,2,···,M)用于描述組件,φh用于描述支撐結構.利用Heaviside 函數可以表征材料分布如下

其中χm,χh,χv分別表征第m個組件、支撐結構和孔洞的材料分布.故任意點的材料屬性可以由如下插值得到

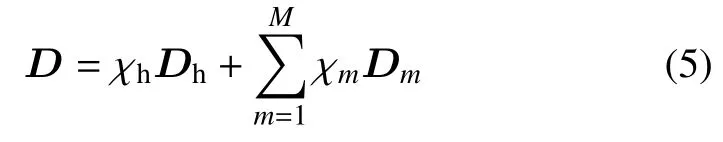
組件q與支撐結構的連接界面可以通過插值表示為

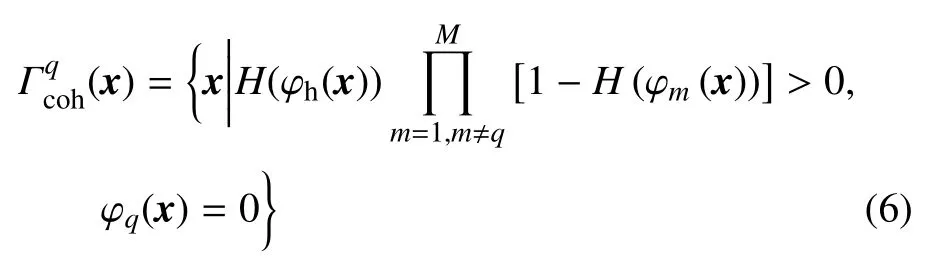
考慮采用距離約束避免組件重疊的情況,式(6)可以簡化為

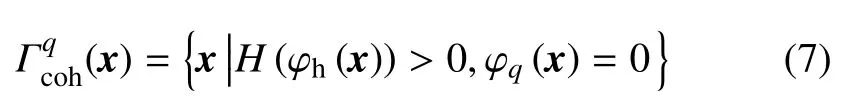
設計域中的全部連接界面可表示為

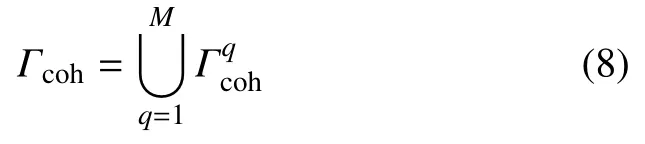
圖6 給出了M=2 時基于水平集的多相材料和連接界面的表征.

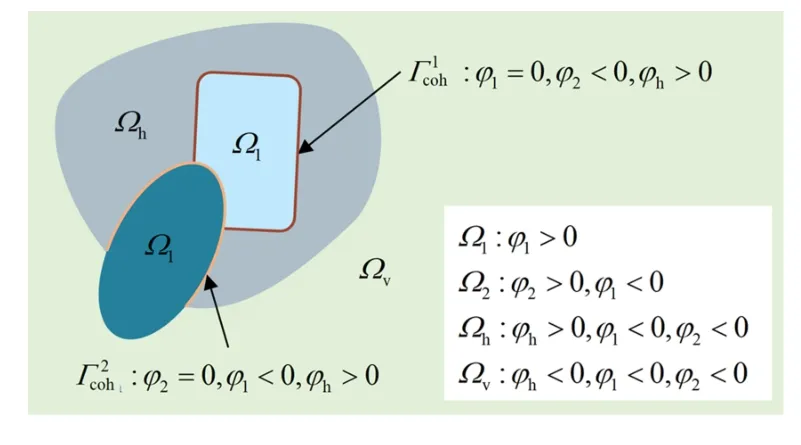
圖6 基于水平集函數的多相材料及連接界面表征Fig.6 Multiphase material and interface characterization

1.3 連接界面內聚力模型

內聚力模型在斷裂力學中被廣泛應用于描述多相材料結構的連接界面,表征了界面之間的黏結力[32]和張開位移之間關系的.本文所采用的指數型內聚力模型[33](見圖7) 基于光滑的非線性函數,可以描述界面的初始彈性階段和軟化階段,并且考慮了界面法向張開位移和剪切方向位移的耦合.

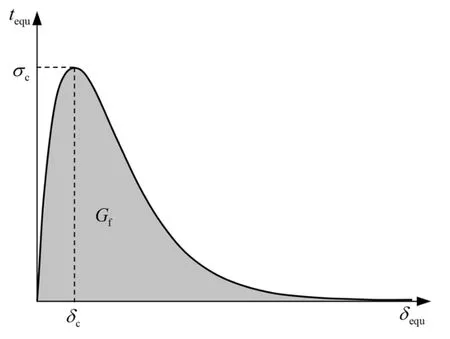
圖7 指數型內聚力模型示意圖Fig.7 Schematic illustration of exponential cohesive zone model

如圖8 所示,二維結構的材料連接界面從初始位置受力張開,界面上的P點在張開后移動到點P+和P-.

圖8 連接界面張開示意圖Fig.8 Schematic illustration of interface’s opening

界面間的黏結力t可表示為

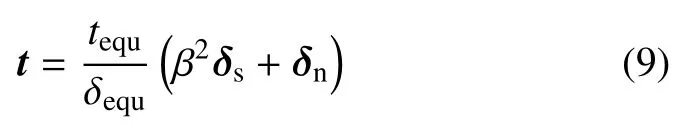
其中,δs和δn分別表示界面剪切方向的位移向量以及法向張開位移向量,tequ和δequ分別表示等效界面黏結力和等效界面張開位移,其表達式如下

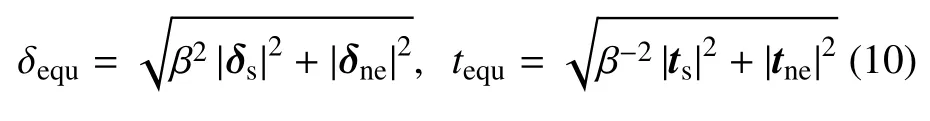
其中,β 是調節法向及切向位移耦合關系的權重系數,δne和tne分別表示連接界面上的有效張開位移和載荷向量

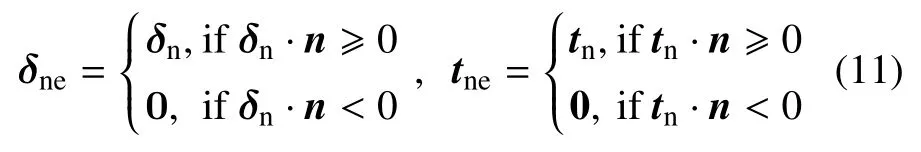
其中,n是界面的法向量.

等效界面張開位移和等效界面黏結力中只考慮了界面的法向拉伸以及剪切量的作用,因而排除了界面受壓發生破壞的情況.tequ和δequ滿足如下關系式

其中,σc是內聚力模型中的界面力的峰值,δc是與之對應的界面張開位移,e是歐拉數.Gf是斷裂能,是tequ在δequ從零到無窮的積分,Gf=eσcδc就是圖7中的陰影部分的面積.

1.4 擴展有限元方法及非線性問題求解

由于本文采用內聚力模型描述連接界面的力學性能,當計算結構響應時,需要對界面的張開位移(即界面處位移場的強間斷)進行準確描述.擴展有限元法[34](extended finite element method,XFEM) 通過在相關節點引入附加的位移自由度并利用間斷的擴充形函數進行位移插值,可以在固定網格下描述位移場的間斷屬性.

圖9 中,連接界面穿過結構化有限元網格,在被切割的單元節點上引入的附加自由度,用于插值界面的張開位移.

圖9 擴展有限元附加自由度示意圖Fig.9 Schematic illustration of XFEM and additional degrees

結構中除界面以外的任意點x的位移可以由有限元的節點位移和附加自由度的位移插值得到

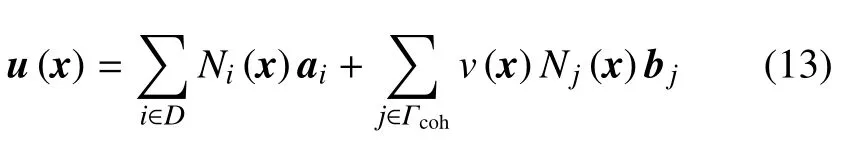
其中,D指設計域,Γcoh表示被界面切割單元的節點集合,Ni和Nj為標準有限元的形函數,ai和bj分別是標準有限元自由度和附加自由度,v(x)為移軸后的間斷函數.界面上任意點x的張開位移向量udisc在全局坐標下可以表示為

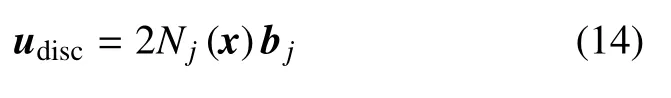
而法向和切向的界面張開位移向量可表示為

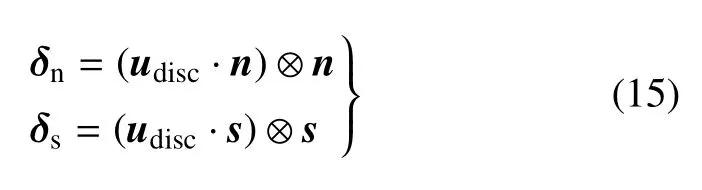
在平衡狀態下,考慮材料連接界面張開的多相材料結構的虛功原理表示為

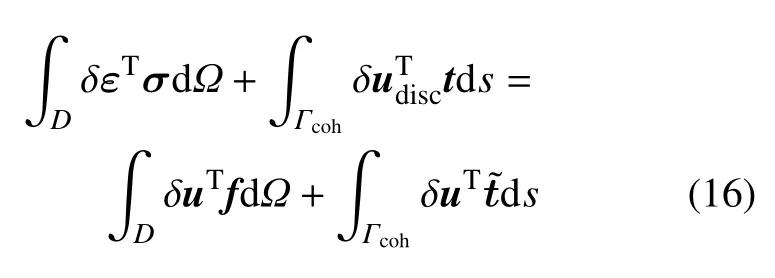
其中,σ和ε為應力和應變向量,f為體力,～t是結構所受的邊界力;δu,δudisc和δε分別為虛位移,界面張開虛位移和虛應變.

在數值計算中,材料連接界面為零水平集與離散網格的交點所連成的折線,進而將包含位移間斷的有限單元三角化為若干子單元進行高斯積分.因為內聚力模型的非線性,本文采用增量形式的求解格式,將殘差表示為R=fint-λfext(其中λ 是載荷因子) (參考文獻[21-23])的形式.具體來說,第k+1 個增量步的殘差力向量可以在第k增量步上展開為如下表達

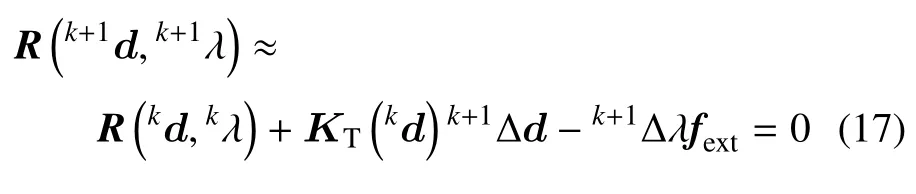
其中,KT=?R/?d表示切向剛度矩陣,上標k+1 和k表示增量步編號,k+1Δd=k+1d-kd,k+1Δλ=k+1λ-kλ.在每個增量步中,采用Newton-Raphson(N-R)算法迭代搜索結構的平衡狀態.

2 拓撲優化問題列式

本節基于速度場水平集方法和參數化的水平集函數建立拓撲優化列示,見方程(18)

對于支撐材料,在水平集網格上定義了一組對應其水平集函數φh的速度設計變量,即1,2,···,n,其中,n為水平集網格節點的數目).支撐材料邊界的法向演化速度可以通過設計變量的雙線性插值得到:

對于可變組件,超橢圓長短軸和階數a,b,η,及其位置(x0,y0)和角度θ 為設計變量.每個組件對應一組設計變量γm,可以確定當前組件的水平集.將組件的參數和基體結構零水平集的演化速度作為協同優化問題的設計變量.

結構的外力功可以表示為材料中存儲的應變能和材料連接界面力所做功的和,即

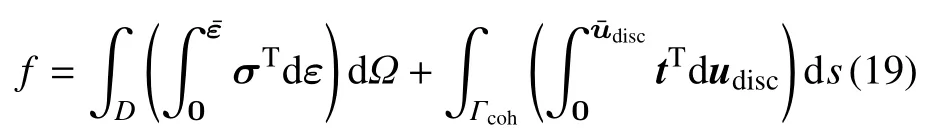
約束函數g1約束支撐材料的體積,其中表示給定的支撐材料體積分數值.約束函數g2和g3分別是組件的非重疊約束和最小距離約束.非重疊約束[12]g2將組件約束在設計域之內.g3為距離約束,使任意兩個組件之間的距離(即兩個超橢圓中心的距離與各自中心到頂點(見圖3) 的距離之差) 大于對于不同的組件可以采用不同的值.K為總增量步,和表示支撐材料邊界演化速度的下界和上界,其值受限于CFL 條件所規定的最大演化步長.本文使用MMA 優化求解算法[28]更新設計變量(水平集網格點上的速度設計變量)并通過插值獲得結構邊界的演化速度,然后使用快速行進方法(fast marching)將這些邊界速度外推到整個域,進而基于Hamilton-Jacobi 方程

更新支撐材料拓撲.組件的水平集函數在每次參數更新后重新構建.

3 靈敏度分析

本節在速度場水平集法框架下,推導目標及約束函數對于速度設計變量的靈敏度.首先將目標函數表示成各增量步對應值的疊加,即考慮平衡方程,建立優化問題的拉格朗日函數

通過將式(21)對狀態變量求導,可得伴隨方程.求解伴隨方程可得伴隨變量(見文獻[23]).最終,目標函數的對支撐材料速度設計變量的靈敏度可表示為

其中,參數ξ3=?D/?φh為材料矩陣對于支撐材料水平集的導數,且利用其中的δ 函數,將域積分的靈敏度轉換成沿零水平集的線積分形式.由于組件由超橢圓參數組γm直接控制,因此目標對設計變量的靈敏度可通過鏈式法則

得到,其中下標m=1,2,···,M,表示組件的相關參數.此外,由于組件的非重疊約束及距離約束的靈敏度只依賴于組件設計變量,同樣可以通過鏈式法則獲得.

4 數值算例

本章在平面應變假設下考慮包含內嵌組件的懸臂梁及MBB 梁拓撲優化問題.支撐材料(材料1)和組件材料(材料2) 的剛度分別為E1=30 000,E2=90 000,泊松比為ν1=ν2=0.15.為避免有限元分析中剛度矩陣的奇異,孔洞相的材料參數設置為E3=10-6,ν3=0.15.內聚力連接界面的參數設置(見方程(12))如下:Gf=0.05,界面力峰值σc=1,對應的界面張開位移峰值δc=Gf/eσc=0.018 4,內聚力模型中界面法向張開位移和切向張開位移耦合的權系數β=2,界面的受壓剛度設置為大常數dn=108,以避免界面受壓時發生穿透現象.所有算例都通過位移進行加載,在非線性有限元分析中,位移載荷通過20 個增量步逐步增加至dP=0.05.數值算例全部采用邊長為10 的正方形雙線性單元對設計域進行離散,并采用與有限元網格重合的水平集網格進行拓撲優化.設置演化步長0.5 倍水平集網格尺寸;為了保證水平集函數的符號距離特征,對支撐材料的水平集函數φh每3 個迭代步進行一次初始化;組件的水平集函數每次參數更新后都重新生成.

4.1 懸臂梁結構拓撲優化

圖10 給出包含內嵌兩個超橢圓組件的懸臂梁結構設計問題示意圖.寬800、高400 的懸臂梁結構左邊固定,在右邊中點施加非零位移.

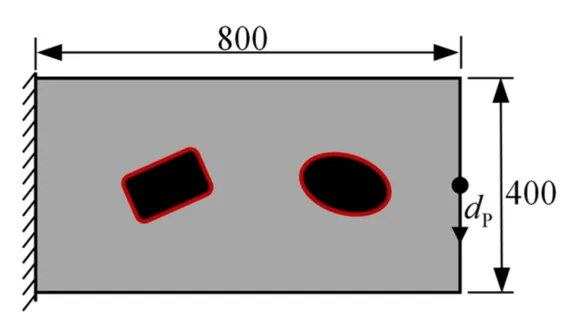
圖10 懸臂梁結構示意圖Fig.10 Schematic illustration of cantilever beam structure

在組件形狀、布局及支撐材料拓撲協同優化過程中,可變組件和支撐材料的拓撲演化互相影響,不同的初始構型演化出不同的結構.初始時采用了如圖11(a)的初始構型對懸臂梁結構進行優化(支撐材料引入稀疏分布的較大孔洞).

圖11 拓撲優化不同的初始解Fig.11 Different initial designs

圖12 為在此初始結構下協同優化迭代的兩個中間結果及第一主應力分布圖.如圖12(a) 所示,由于孔洞的存在以及支撐材料的體積約束在優化的初始階段占據主導,組件(圖12 中超橢圓曲線表示的部分)被困在局部區域.并且隨優化的進行,如圖12(b)所示中間設計,結構左側的組件移動到不受力的孔洞區域以避免組件的連接界面發生拉伸及剪切破壞造成結構的剛度損失.該局部解雖然不會發生界面破壞,但由于功能性組件并未承載,并未對結構的承載能力提供貢獻.

圖12 懸臂梁優化迭代中間設計的第一主應力分布Fig.12 The first principal stress distribution in intermediate designs of cantilever beam

為了避免這種情況的出現,本文采用了兩個階段的優化策略:首先在設計域布滿支撐材料并對組件的布局和形狀進行優化,為了避免組件過于靠近導致在孔洞演進時發生重疊,設定距離約束的值C0=60;經過一定步數的迭代,組件會移動到受壓區域,此時在支撐材料域內引入加密分布的均勻小孔洞(見圖11(b)),進行組件和支撐材料結構的協同優化.

表1 給出了3 種初始構型對應的優化結果,初始的組件均為半徑50 處于不同位置的圓,限制a,b∈[40,50],且限定第一階段的迭代步數為100 步.在3組優化結果中,兩組件均演化為a,b=40,η=6 的超橢圓.但是由于組件參數和支撐結構的相互影響,使用上述優化策略得到的最終的拓撲結構和目標值有所不同,但是組件及其界面均處于受壓區域(優化結果與圖12(b)相似).

表1 支撐材料體積分數約束為0.4 時,不同初始組件位置的懸臂梁結構優化Table 1 Optimization of the cantilever beam structures with different initial components’positions, =0.4

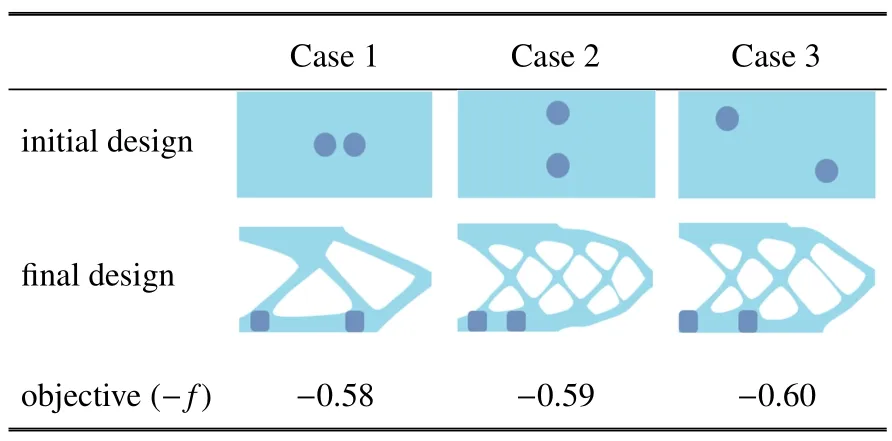
表1 支撐材料體積分數約束為0.4 時,不同初始組件位置的懸臂梁結構優化Table 1 Optimization of the cantilever beam structures with different initial components’positions, =0.4

進一步考察不同支撐材料體積分數對優化結果的影響,使用與表1 中Case 1 相同的初始構型,給定支撐材料體積分數為0.45 和0.5,得到如圖13 所示的懸臂梁拓撲結構.從圖13 中可見,不同支撐材料體積用量下,組件的最優布局及形狀基本不變,且當支撐材料體積為0.5 時其拓撲展現出明顯的非對稱性.

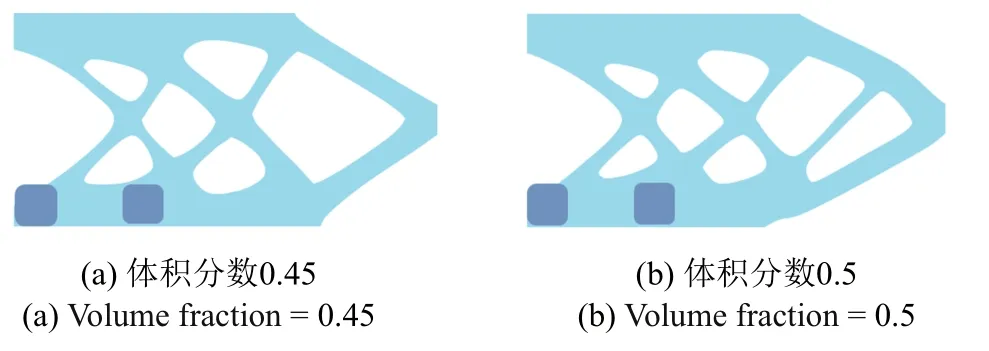
圖13 懸臂梁拓撲優化結果Fig.13 Optimized designs of the cantilever beam

4.2 MBB 梁結構優化

本小節以MBB 梁結構優化為例討論了組件的形狀對優化結果的影響.圖14 給出包含內嵌組件的MBB 梁結構設計問題示意圖.寬800,高400 的MBB梁結構左邊約束水平方向位移,右下角點約束垂直方向位移,并在左下角施加非零位移.

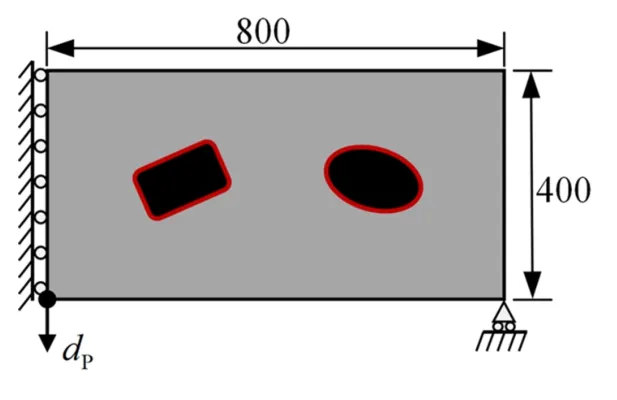
圖14 MBB 梁結構示意圖Fig.14 Schematic illustration of MBB beam structure

首先,采用與表1 中Case 1 相同的初始構型(水平并列的半徑50 的圓) 和優化策略及參數,得到如圖15(a)的MBB 梁結構設計,目標值為-0.47,兩組件演化為a,b=40,η=6 的超橢圓.經主應力分析,該優化設計中的組件及其界面主要承受壓力作用(見圖15(b)).

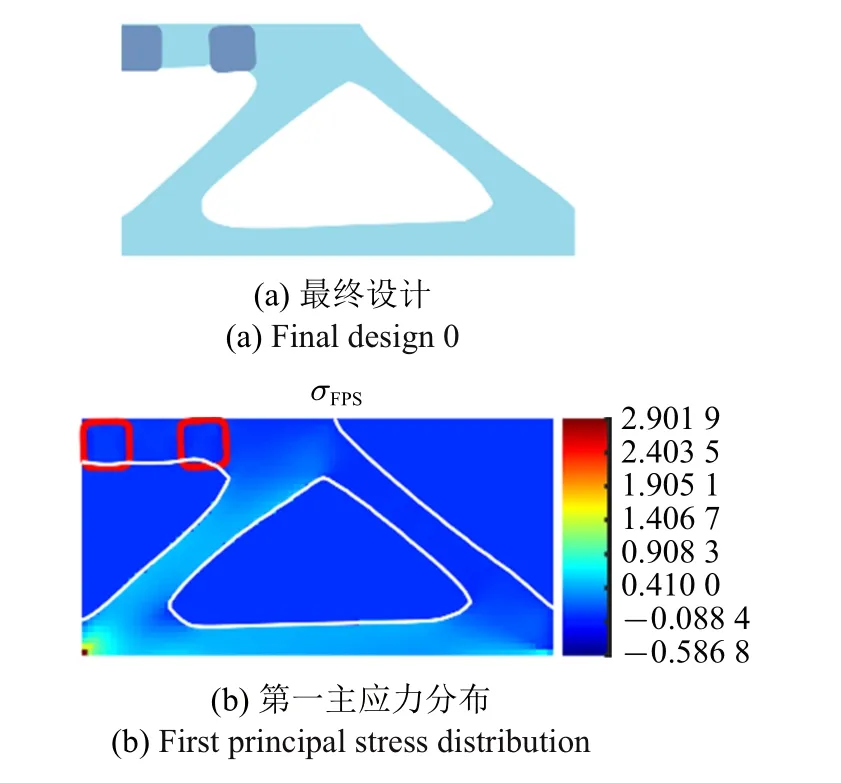
圖15 MBB 梁的優化設計Fig.15 Optimized design of the MBB beam

進一步,在優化過程中將組件1 的形狀限定為橢圓形,組件2 的形狀限定為近似的矩形(即令η1∈[2,2.5],η2∈[4,6]),同樣采用與表1 中Case 1 相同的初始構型和參數進行協同優化,得到如圖16 所示的迭代歷史和優化設計.

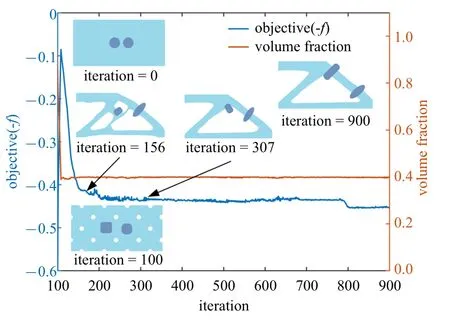
圖16 MBB 梁結構的優化迭代過程Fig.16 Optimization iteration process of MBB beam structure

兩階段優化策略中,第一階段依舊限制a,b∈[40,50],但是由于限制了兩個超橢圓組件的不同的η范圍,在此階段內組件的形狀及布局并未產生顯著變化.在第二階段對組件形狀、布局和支撐材料拓撲進行協同優化,并設定組件的長短軸a,b∈[30,80].在協同優化的初始階段,支撐材料逐漸減少至給定的體積約束值,在此過程中目標值-f隨之增大.體積約束滿足之后,通過結構拓撲和組件特征的優化,得到了MBB 梁優化設計.同樣地,在優化設計中,經主應力分析,組件及其連接界面主要承受壓應力作用.兩個組件均演化為長軸80,短軸30 的超橢圓,且組件與支撐結構的界面趨于曲率較小的直線或曲線.

雖然本算例及4.1 節算例均以雙組件布局與支撐結構拓撲的協同優化作為典型對象進行研究,但本文所采用的有限元分析及所提出的優化方法對包含更多組件的結構優化問題仍然適用.根據對已有優化結果的觀察,當組件數目增多時,多組件的布局仍可能分布到結構的受壓區域,且優化結果中連接界面趨向于曲率較小的曲線.另一方面,隨著組件數目的增加,由于優化過程中組件距離約束等的作用,多個組件之間的相互影響更為復雜,設計問題可能具有更多的局部最優解.

5 結論

材料連接界面的力學性能對多相材料結構的力學性能及其優化設計影響顯著.本文基于擴展有限元及內聚力模型考慮材料連接界面的力學性能,使用超橢圓描述了有一定設計自由度的、形狀及布局可變的內嵌組件,提出了基于水平集描述的內嵌組件形狀、布局及支撐材料拓撲的協同優化方法,本文給出了優化問題的解析靈敏度,并基于數學規劃法在速度場水平集方法框架下對優化問題進行求解.通過嵌入組件的懸臂梁和MBB 梁的優化驗證了優化策略的可行性.

數值算例顯示,考慮連接界面性能的情況下,組件及界面主要處在壓應力作用區域,且連接界面最優形狀呈現為曲率較小的光滑曲線,該設計避免界面發生破壞進而有效提高了結構的承載力.基于此考慮連接界面的協同優化框架,任意形狀的多組件內嵌結構的優化也可以通過引入B 樣條的組件描述實現.