風力發電系統的隨機響應

梁相玲,葉正偉,秦旺,鄧生文

(蘭州交通大學 數理學院,甘肅 蘭州 730070)

隨著全球經濟的增長,新能源的開發利用為世界能源危機與環境污染問題帶來了解決方法,其中風能是之一。風能具有儲存量大,短周期,低污染,范圍廣等特點,其主要應用于發電[1-3]。近年來,風力發電已涉及到各個領域,其效果得到了眾人的認可,故國內外眾多研究者都積極建模以便了解其原理與不足[4-5]。雖然通過多年來的研究分析使得風力發電系統已逐步完善,但是對風力發電系統在不同的工作環境中受到不確定自然條件的隨機擾動的因素卻考慮甚少,使得其輸出功率與實際存在差異,故需要考慮和分析影響風力發電的因素,以便尋求風能被有效利用的措施。本文基于轉子系統通過變換引進參激與外激得到隨機風力發電系統,主要依據隨機平均法與哈密頓理論以及最大李雅普諾夫指數法,分析隨機響應即隨機穩定性及其Hopf分岔,最后分析了分岔參數并展示其數值模擬圖。

1 風電的隨機動力系統

1.1 隨機模型

本文基于機械系統風力渦輪轉子系統,建立的簡易風力發電系統模型如圖1所示[6-7]。

圖1 簡易風力發電系統模型Fig.1 Simple wind power generation system model

轉子方程為

(1)

式中:α是風力渦輪轉子的角加速度;w是轉子的角速度;δ是角度。所以可看到

Jα=Mm-Me-MD

(2)

式中J,Me,Mm,MD分別是發電機轉子的慣性力矩(包括轉子的原動力)，發電機主軸上的機械轉矩，機械制動電磁轉矩，阻尼力矩[6-7]。

由式(2)得

(3)

由于J可以由A表示,所以方程(3)可表示為

(4)

式中：A為慣性時間常數；f0為頻率；δ單位為rad；Mm、Me和MD表示單位值。

力矩M由功率P表示為

(5)

故有

(6)

式中Pm,Pe,PD分別表示機械功率,電磁功率,阻尼功率,且都以單位值表示,其中基值以kV/A為單位。

其中

(7)

式中D為阻尼系數。

(8)

故所要研究的隨機風力發電系統為[8-9]

β1δ(t)ξ(t)+β2ξ(t)

(9)

式中:ξ(t)是高斯白噪聲,滿足〈ξ(t)〉=0,噪聲強度為2D;β1和β2是控制參數。

故可得系統的狀態方程為

(10)

1.2 Hamiltonian 系統

令δ(t)=q(t),ω(t)=p(t),則式(10)可寫為

(11)

則方程(11)的總能量為[10]

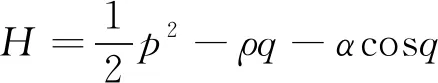
(12)

1.3 漂移系數與擴散系數

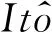
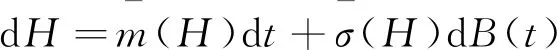
(13)

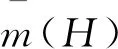
Ω={(q1,…,qn,p2,…,pn)|H

(q1,…,qn,0,p2,…,pn)≤H}

(14)

計算可得

(15)

(16)

2 穩定性分析

其穩定性分析主要依據最大Lyapunov指數法。首先需要把Lyapunov指數引用到隨機微分方程中,需要做以下推導[13-14]：

(17)

(18)

為了得到其最大Lyapunov指數,可將方程(13)在H=0處表示成線性化形式:

(19)

其解為

(20)

則其最大Lyapunov指數為

(21)

故得

(22)

由式(22)可得系統在解H=0處,當λ<0時,系統是局部漸近穩定的;當λ>0時,系統是不穩定的;當λ=0時,系統發生分岔。

3 隨機分岔

根據其擴散系數與漂移系數可得方程(11)的平均FPK方程為

(23)

則平穩概率即式(23)的解為

f(H)=CHηexp[-H]

(24)

式中C是歸一化常數，且通過計算得

(25)

接著可得聯合概率密度函數為

(26)

對于隨機非線性動力系統,分岔類型可定義為D分岔和P分岔,兩者完全由υ區分。選擇γ作為參數描述隨機分岔現象[14]。

1)D分岔點的計算:根據之前分析,當系統完成D分岔時υ=-1。則有

υ=cl-?l=

(27)

2)P分岔點的計算:同理，P分岔點公式為

υ=cl-?l=

(28)

4 數值模擬

選擇γ作為分岔參數,令α=1,ρ=0.2,D=0.5,β1=0.5,β2=1。數值模擬平穩概率密度函數與聯合概率密度函數在參數的不同取值下的圖像如圖2—圖6所示。

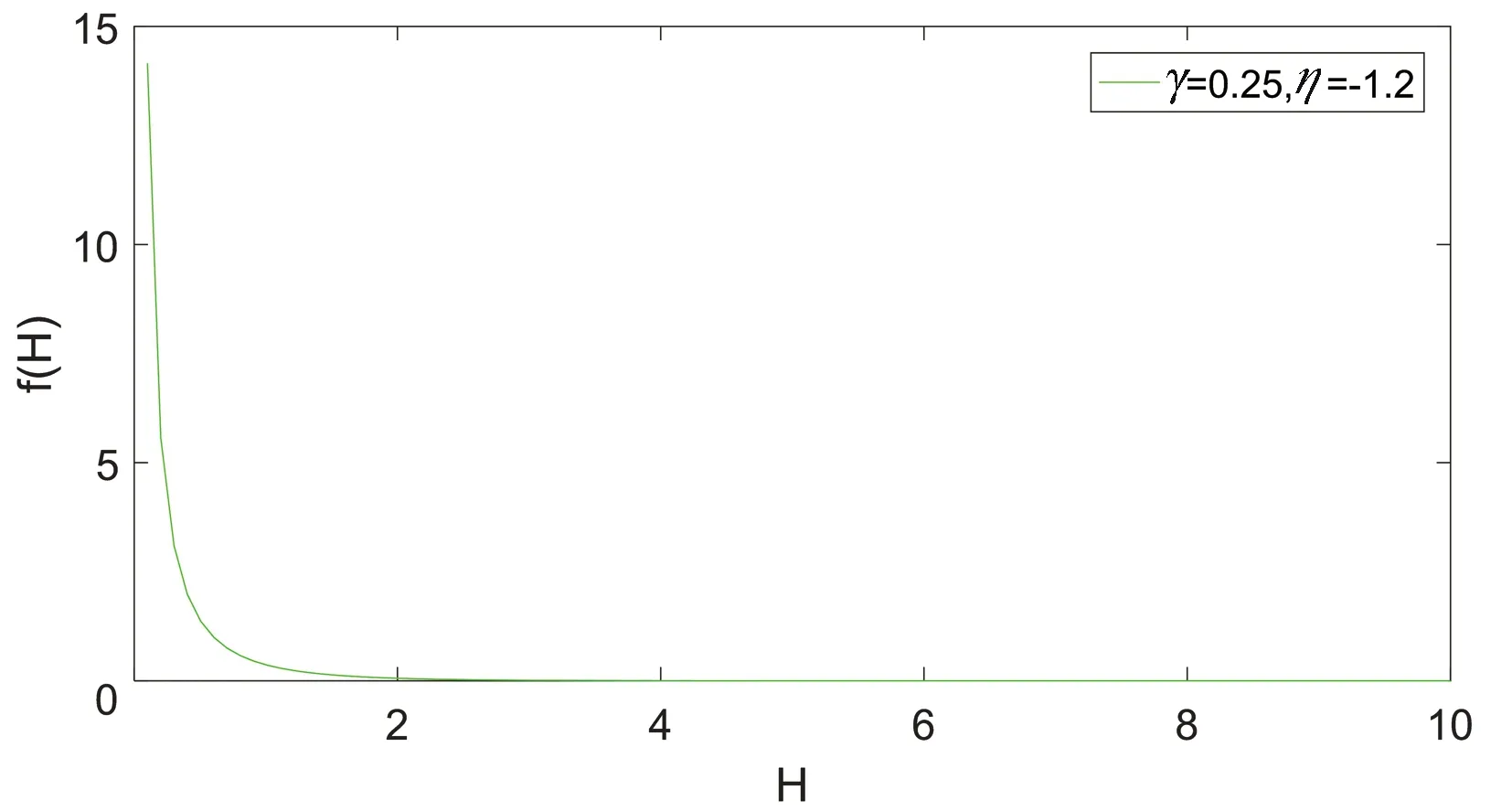
圖2 γ=0.25時的平穩概率密度函數Fig. 2 The stationary probability density function when γ=0.25

圖3 γ取不同值時平穩概率密度函數 Fig. 3 The stationary probability density function with different value of γ

綜合圖2和圖3可以看出，隨著參數γ取值的減小其平穩概率密度函數是單調遞減的且逐漸趨向平緩,即γ經過了臨界點γ=0.208 3后函數的圖象由單調遞減變為單峰狀函數,并且隨著γ的持續減小,函數的谷峰逐漸趨向平緩,由此說明系統在臨界點γ=0.208 3后發生了Hopf分岔。

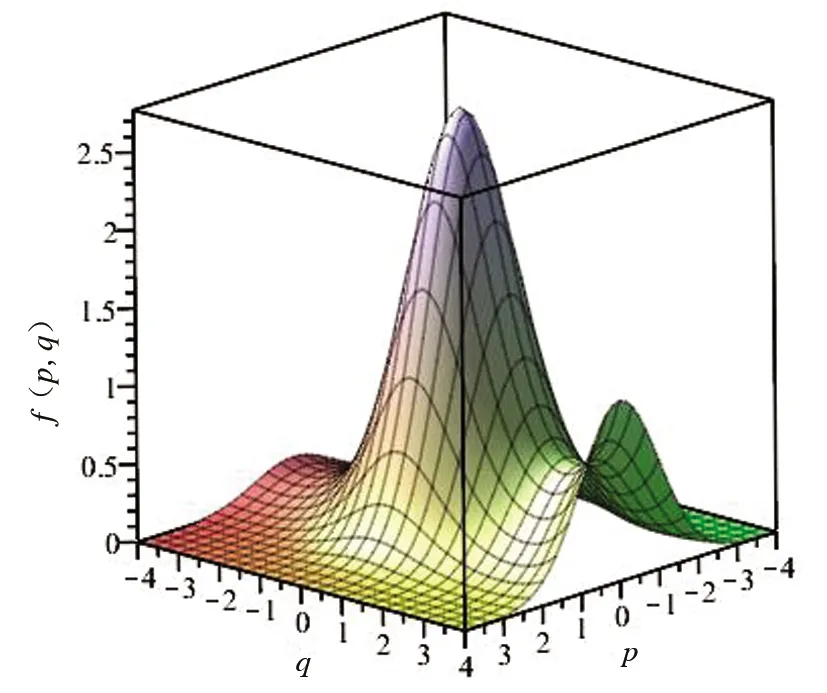
圖4 γ=0.208 3時的聯合概率密度函數 Fig. 4 The joint probability density function when γ=0.208 3

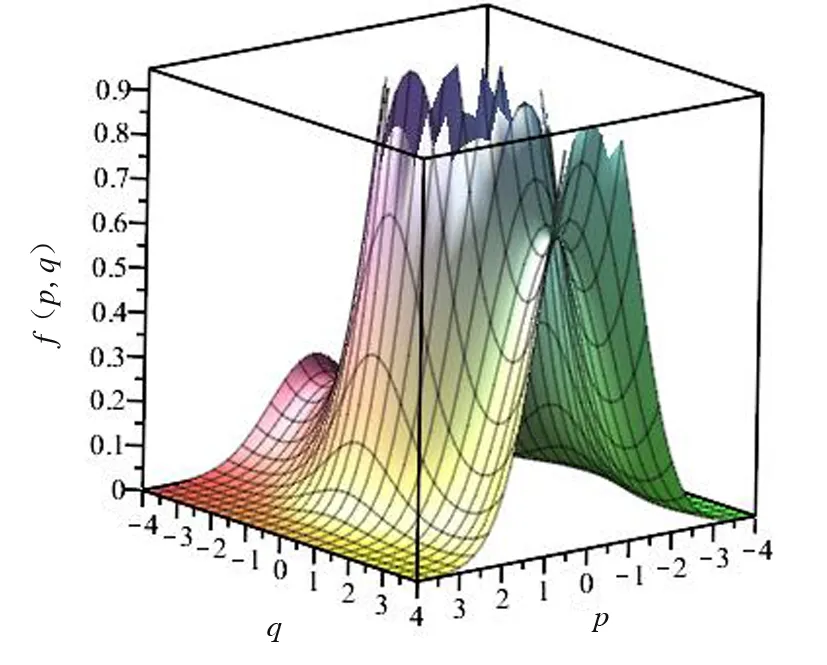
圖5 γ=0.208時的聯合概率密度函數Fig. 5 The joint probability density function when γ=0.208

圖6 γ=0.2時的聯合概率密度函數Fig.6 The joint probability density function when γ=0.2

綜合圖4、圖5和圖6可以看出，當γ=0.208 3時,函數圖象是一個單峰狀；當γ=0.208和0.2時,呈火山口狀,這說明系統在臨界點γ=0.208 3后發生了Hopf分岔。

5 結束語