HRRP稀疏自編碼器深層特征與散射中心特征的關聯性研究

霍超穎, 閆 華, 馮雪健, 殷紅成, 邢笑宇, 陸金文

(北京環境特性研究所電磁散射重點實驗室, 北京 100854)

0 引 言

雷達一維高分辨距離像(high resolution range profile,HRRP)揭示了目標沿視線方向散射中心的分布,含有非常豐富的目標距離向結構信息,從中可以提取出散射中心的數目、位置、強度、徑向長度等參量,是雷達目標識別重要的特征來源。此外，HRRP還具有易于獲取和處理的優勢,因此基于HRRP的目標特征提取是雷達目標識別領域的一個重要研究方向。針對HRRP的特征提取與識別問題,已經有很多學者進行了廣泛的研究,主要包括傳統的特征識別方法和近些年發展起來的深度學習識別方法。

傳統基于HRRP的特征提取方法主要是提取平移、尺度不變性等特征,包括強散射中心特征、熵值特征、中心矩特征、功率譜特征等[1],然后對特征進行有效性評價,再將優選后的特征組合成特征矢量,通過設計適當的分類器來完成目標識別。識別過程中使用較多的分類器包括模板匹配法[2]、支持向量機[3-4]等。這些方法均需要提取穩定的特征,因此很容易受到噪聲的影響。后期又出現了基于主成分分析方法[5-6]獲得樣本子空間投影特征,通過構建最小化重構誤差來實現HRRP目標識別方法。上述算法均是基于數學或物理模型由人工設計得到的,雖然物理含義比較明確,但是主觀性較強,對數據的描述能力不足,并且缺乏通用性,導致識別率難以提高,泛化能力較低。

隨著深度學習的快速發展,深層網絡已經在雷達數據處理中得到廣泛的應用[7],通過層次化的非線性網絡結構可以從數據中學習到抽象特征,從而挖掘出數據的內在結構,提升分類識別效果。目前,已經有一些學者將深度學習應用到HRRP的特征識別中。文獻[8-11]均使用卷積神經網絡(convolutional neural networks,CNN)從HRRP序列圖像中學習到穩定特征,進而實現目標的分類識別,該方法能夠在信噪比較低情況下保持較高的識別準確率,具有較強的魯棒性。文獻[12-16]使用自編碼器網絡實現了HRRP的特征學習,可以獲得穩健有效的識別特征,從而提高識別準確率,并具有很好的降維和泛化能力。雖然上述研究均表明利用深度學習網絡獲得了穩定特征,但是,并沒有說明穩定特征的含義,更沒有對深度學習網絡的隱層參數進行物理解釋,因此無法實現對雷達數據本質特性的深度學習,以及后續指導網絡的優化改進,從而限制了深度學習在雷達數據處理中作用效能的真正發揮。

針對上述問題,本文主要針對HRRP稀疏自編碼器深層網絡與散射中心特征的關聯性開展研究,挖掘網絡隱層特征參數的物理意義。首先給出了針對HRRP的多層稀疏自編碼器網絡結構,然后通過定義的一種綜合權重系數和降維特征與散射中心特征進行對比分析,找到網絡參數與散射中心特征的關聯關系,以及深度學習網絡實現了哪些具體的數據挖掘或特征提取工作。最后,通過分析網絡參數對學習訓練和特征提取結果的影響,指導后續目標特征提取與識別中網絡參數的選擇。

1 HRRP稀疏自編碼器網絡結構與原理

1.1 稀疏自編碼器網絡結構

自編碼器是一種無監督學習方式,其無監督性在于將輸入數據進行編碼和解碼后,通過使重構誤差最小化來完成網絡參數的訓練。自編碼器在學習過程中能夠保留樣本的主要信息和特征,單層自編碼結構如圖1所示,共有3層結構分別用以表示樣本輸入{x}、編碼輸出{h}以及解碼輸出{xr},通常編碼輸出層l2也稱為隱含層。其中l1與l2中“+1”項表示編碼和解碼過程中的偏置項系數,取值都為1。

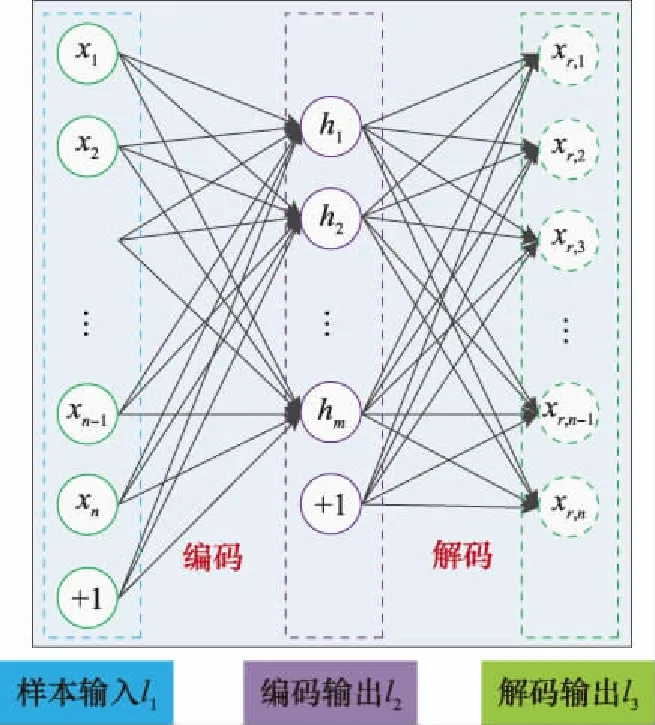
圖1 單層自編碼器結構

編碼和解碼過程寫成函數形式如下所示:

h=f(W1x+b1)

(1)

xr=f(W2h+b2)

(2)

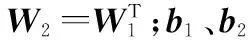
自編碼器無監督學習的目的是不斷更新編碼參數{W1}、{b1}和解碼參數{W2}、{b2}使得樣本輸入重構誤差最小化,重構誤差用式(3)表示的損失函數Fcost來衡量:

(3)

式中:n為輸入樣本個數。

為了提高自編碼器的自動學習樣本特征能力,引入稀疏表達的思想在傳統自編碼的基礎上加入稀疏性約束形成稀疏自編碼器。這里稀疏約束指的是對隱含層l2的神經元進行約束,通過對其大部分輸出進行抑制從而達到學習網絡的稀疏效果。

與自編碼器不同,稀疏自編碼器學習過程中不但要更新編碼參數{W1}、{b1}與解碼參數{W2}、{b2},還要求解l2層內神經元的平均活躍度,求解公式如下所示:

(4)

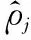
再加入稀疏限制條件:

(5)

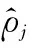
(6)

此時總的損失函數Fsparse(W,b)可以寫成：

(7)

式中:β為一個常數,作為懲罰因子的權重參數。在網絡參數迭代尋優過程中,本文采用L-BFGS(limited BFGS)算法[17]進行優化,L-BFGS算法是對傳統BFGS算法的一種優化,大大降低了系統的內存消耗與計算復雜度,增強了算法的多維數據處理能力,加快了算法的收斂速度。

1.2 HRRP多層稀疏自編碼器網絡設計

寬帶雷達信號經過脈沖壓縮后可獲得目標散射點在徑向距離上的高分辨率,從而形成目標的高分辨HRRP。假設雷達發射信號為線性調頻信號,經過解線性調頻后得到的目標頻率響應可以表示為各個散射點的頻率響應之和,實際中只能得到有限個采樣值,設頻率采樣寬度為Δf,得到相應的離散頻率形式為

(8)

雷達回波數據中的散射中心參數{K,rk,σk}(k=1,2,…,K)表征散射點的個數、散射點位置和回波強度,反映了特定姿態下目標散射點沿雷達視線的一維分布情況,提供了目標的徑向結構信息。對N點序列X(n)(n=0,1,…,N-1)直接做快速傅立葉逆變換(inverse fast Fourier transform, IFFT),可得時域序列x(n),即為HRRP,x(n)表示為

(9)

式中：n=0,1,…,N-1。

IFFT后得到是目標的復距離像,由于復距離像的相位對目標的姿態和距離變化非常敏感,具有較大的不確定性,在識別中難以利用,故雷達高分辨距離像識別中采用復距離像取模后的實數距離像

x=[|x(1)|,|x(2)|,…,|x(N)|]T

(10)

隨離散角度變化的多個HRRP數據稱為HRRP歷程數據,可以由下面的數據矩陣來給出:

X=[x1,x2,…,xM]

(11)

式中:M為角度變化的數量,根據基于散射中心的HRRP模型式(9),可以得到X的表達式為

(12)

式中:

(13)

構成的矩陣A稱為導向矩陣(或稱字典),而其每個列向量稱為導向矢量(或稱原子),每個原子對應著在rk位置存在的單個散射中心所形成的HRRP。

由于目標的雷達HRRP具有姿態敏感性,會隨著姿態角的變化而不斷變化,而單層稀疏自編碼器對數據的特征學習能力有限,因此需要設計多層的稀疏自編碼器網絡來對HRRP進行特征學習。HRRP的多層稀疏自編碼器網絡結構如圖2所示,是通過多層稀疏自編碼器連接而成的,層與層之間通過上一層隱含層作為下一層輸入層的形式相連,輸出特征為最后一層的隱含層值,從而可將多個自編碼器堆疊構成深度結構,能夠逐層壓縮或提取數據特征供分析和后續應用。

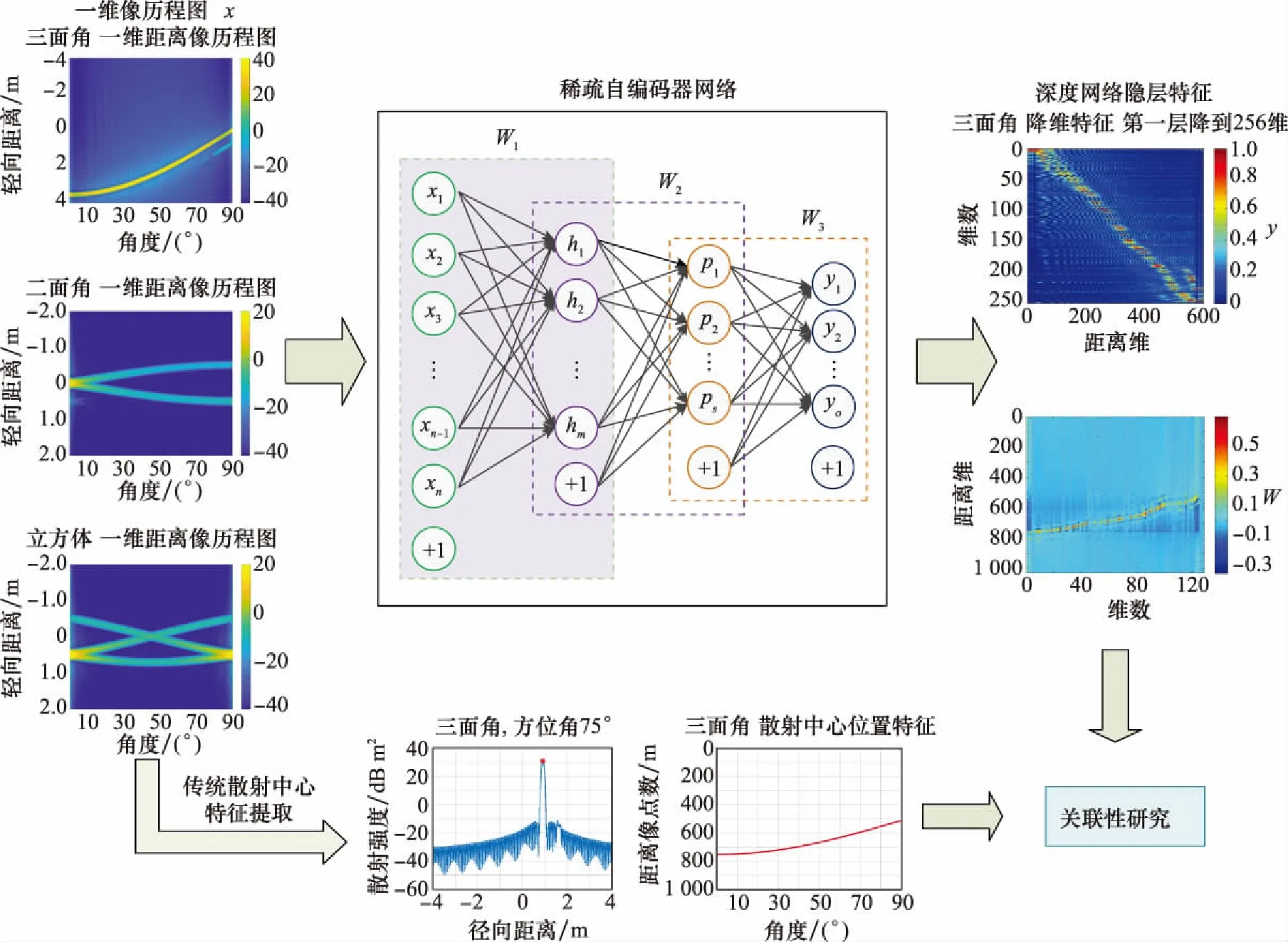
圖2 多層稀疏自編碼器網絡

本文中采用逐層編碼的三層稀疏自編碼器,經過三層稀疏自編碼器網絡之后,可將HRRP數據進行特征降維:

X=f(W1·f(W2·f(W3·Y+b3)+b2)+b1)

(14)

式中:X為HRRP；Y為三層降維后的特征；W1,W2,W3為每一層的權重系數,將三層網絡的權重系數相乘,定義整個網絡的綜合權重系數W為

W=W1W2W3

(15)

不難看出,當激活函數f(·)取恒等函數時,綜合權重系數W與前面定義的字典A完全相同,此時綜合權重系數W即為網絡學習到的字典。那么,對于非線性激活函數f(·),綜合權重系數W與散射中心在距離域的字典A是否相關呢？本文后續內容將通過一系列仿真實驗對該問題進行深入研究。

2 典型標準體HRRP數據集構建與稀疏自編碼器網絡學習

2.1 典型標準體HRRP數據集構建

本文選取三類典型標準體目標進行試驗,分別為三面角、二面角、立方體,然后采用高頻法獲得X波段下的寬帶掃頻數據。三類標準體模型如圖3所示。

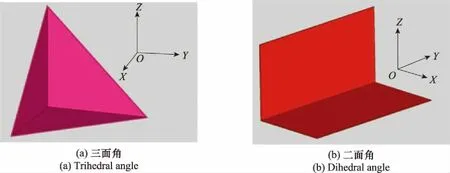
圖3 典型標準體模型

三類標準體寬帶數據仿真條件為:中心頻率10 GHz;帶寬2 GHz;頻率間隔10 MHz;HH極化。入射方位角φ都是0°～90°,角度間隔為0.15°;三面角入射俯仰角θ為45°,二面角和立方體俯仰角為90°。其中,方位角定義為入射方向在X-Y面投影與X軸夾角,俯仰角定義為入射方向與Z軸夾角,如圖3(d)所示。建模方法采用的是物理光學(physical optics, PO)[18]、等效邊緣電磁流(equivalent edge currents, EEC)[19]和彈跳射線(shooting and bouncing ray, SBR)[20]技術相結合對目標進行多次反射計算。尺寸以及其他仿真條件如表1所示。

表1 典型標準體仿真條件

經過HRRP成像處理,可以獲得三類標準體目標的HRRP歷程圖如圖4所示。每類目標的數據集由600組HRRP構成,每組HRRP共1 024個采樣點。

圖4 典型標準體HRRP歷程圖

2.2 典型標準體散射中心特征提取與分析

散射中心是與電磁散射機理相關聯的,幾何繞射理論模型是一種常用的散射中心參數化模型,因此可以基于該模型并利用基于旋轉不變技術的信號參數估計(estimating signal paratheter via rotational invarionce techniques, ESPRIT)算法[21]從寬帶數據中提取出散射中心的位置和強度。ESPRIT算法的基本思想是利用信號子空間的旋轉不變特性,構造兩個完全相同的信號子陣模型,通過特征分解、最小二乘等方法,估計出兩個子陣之間的旋轉算符,進而得到對散射中心參數的估計,具有較好的估計精度和穩定性,且分辨率高,不必進行譜峰搜索,因此常用于散射中心的位置和幅度參數的估計。

三類標準體高分辨散射中心位置特征提取結果如圖5～圖7所示。可以看出,三面角有一個主要的散射中心,主要由三次鏡面反射機理形成;二面角由一個散射中心逐漸變為兩個散射中心,當垂直共邊入射時,主要為鏡面反射機理形成單個“延展型”散射中心,在其他角度下為由邊緣繞射形成的兩個散射中心;立方體在從0°到45°和從45°到90°散射中心的變化過程對稱,先由兩個散射中心變為3個散射中心,再變回兩個散射中心,主要是由立方體不同邊緣的繞射所產生。

圖5 三面角散射中心特征提取結果

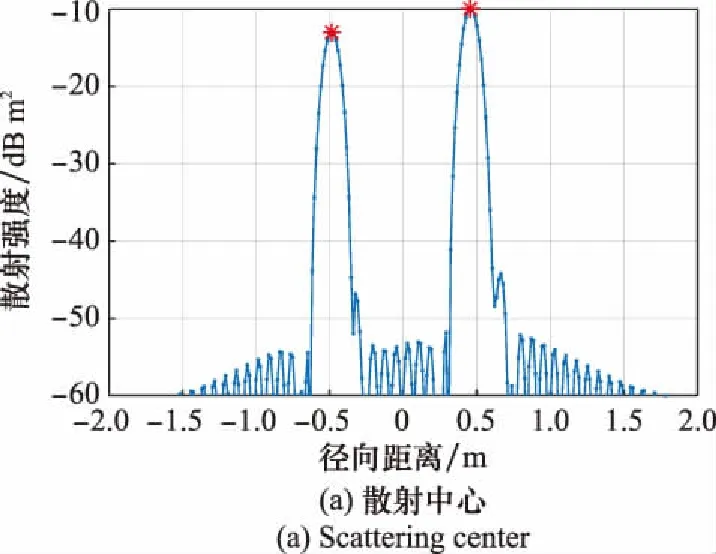
圖6 二面角散射中心特征提取結果

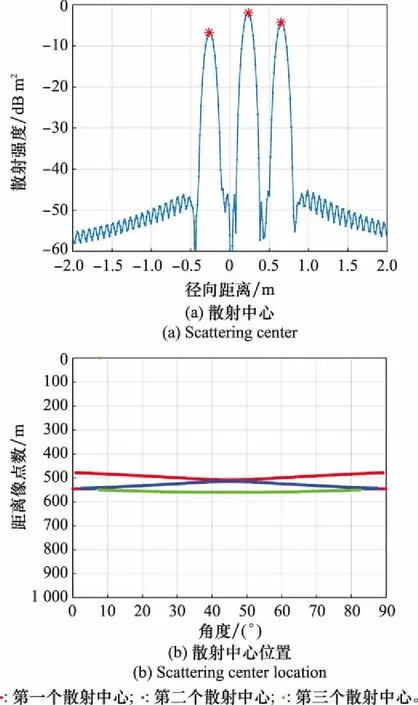
圖7 立方體散射中心特征提取結果

2.3 典型標準體HRRP特征學習與權重系數提取

將三類典型標準體的HRRP歸一化后,作為稀疏自編碼器網絡的輸入,每類標準體目標HRRP的角度范圍從0°到90°,共600組一維像數據,送入深度學習網絡進行訓練。本文中第一層網絡設置隱含層數目為256,第二層網絡設置隱含層數目為64,第三層網絡設置隱含層數目為9,從而實現1 024維距離像到9維特征的學習和降維過程,每層訓練后自編碼器的輸出特征均為該層得到的非監督學習特征。從每一層網絡中提取訓練過程中的權重系數,并進行相乘,可以獲取學習網絡的綜合權重系數W。

三面角、二面角、立方體三類標準體HRRP降維后的9維特征為9×600的矩陣,綜合權重系數為9×1 024的矩陣,將降維特征和綜合權重系數進行二維和一維顯示,如圖8～圖10所示。綜合權重系數矩陣由9個1×1 024的行向量組成,稱每個行向量為綜合權重系數向量。值得注意的是,每個綜合權重系數向量與輸入的一維距離像具有相同的維數。

圖8 三面角深度學習特征提取結果

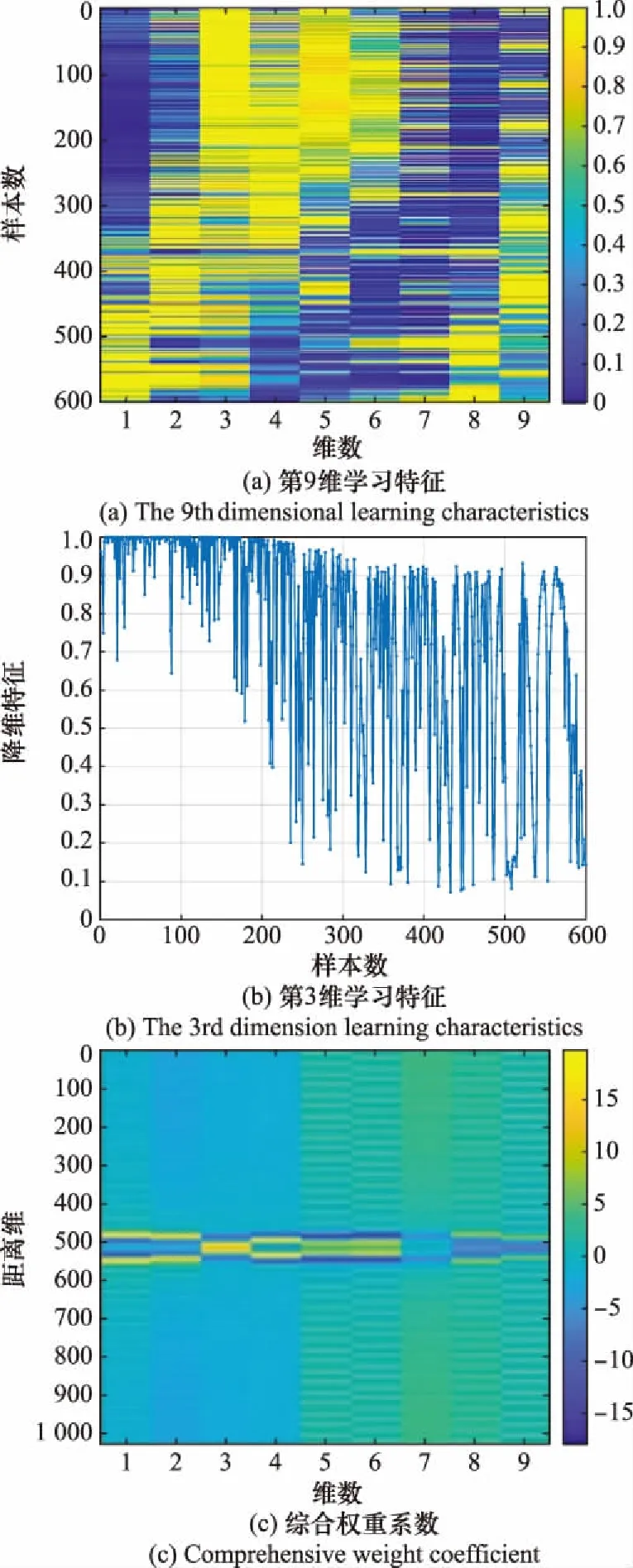
圖9 二面角深度學習特征提取結果

圖10 立方體深度學習特征提取結果

3 稀疏自編碼器深層特征與散射中心特征關聯性研究

3.1 權重系數與散射中心特征關聯關系

從網絡降維過程中提取的綜合權重系數(如圖8～圖10所示)中可以發現,大部分維度的權重系數向量都有比較強的峰值,但其他維度的權重系數向量沒有強峰值,整體權重值都比較低,如圖11所示。由于網絡學習過程中不僅要對信號部分進行學習,還會對噪聲部分進行學習,因此權重系數具有強峰值時則實現了對HRRP強散射中心的訓練,而弱權重系數則會實現對一維像中噪聲的訓練。后續研究過程中需要首先去除噪聲訓練產生的權重系數。

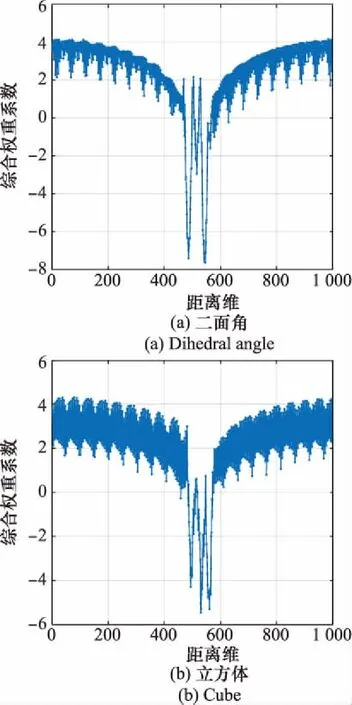
圖11 噪聲訓練權重系數

另外,有些不同維度的權重系數會比較相似,如圖12所示,說明在降維過程中出現了冗余。多層特征學習會減少權重系數之間的冗余度,但是仍然會存在少量的冗余。因此,在關聯性研究之前,需要去除掉冗余的權重系數。

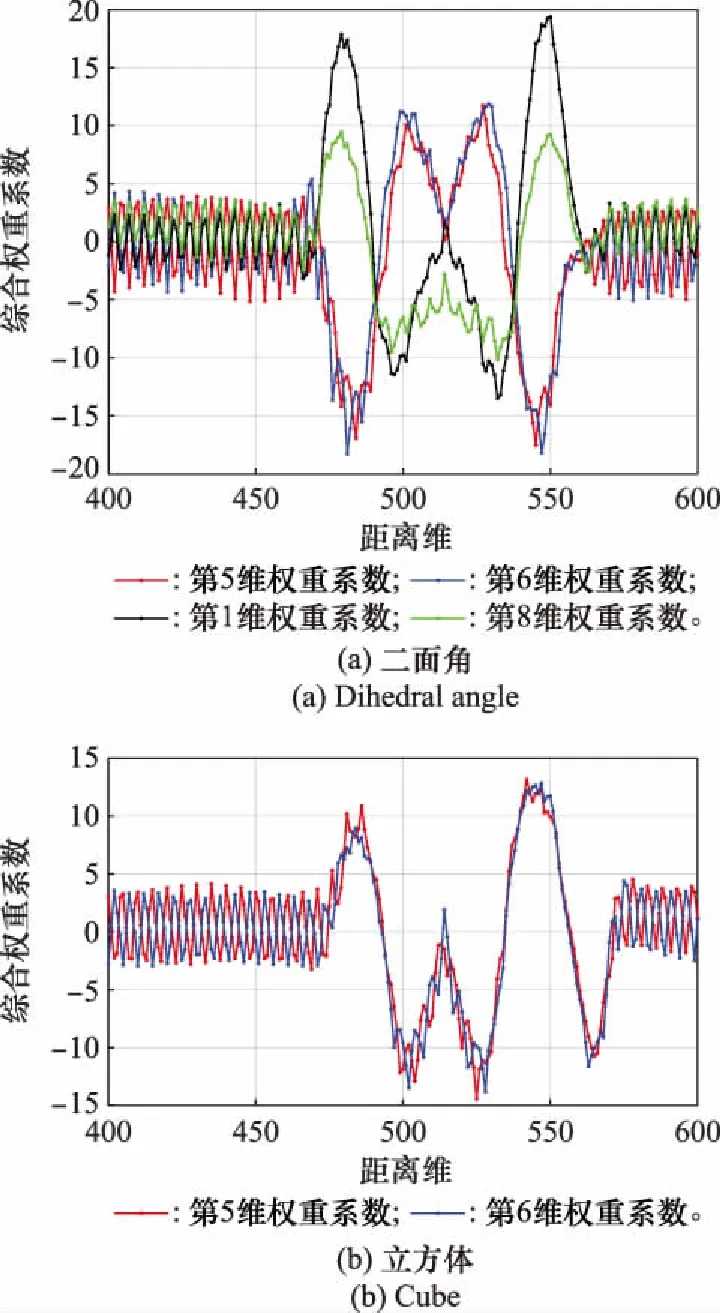
圖12 冗余權重系數

經過分析發現,綜合權重系數峰值在距離維度上的位置與散射中心的位置有很強的吻合性,將去冗余和去除掉噪聲權重系數向量后的權重系數按照散射中心位置隨角度的變化規律重新排序,并與HRRP歷程圖相比,如圖13所示,兩者具有很強的相似性,說明權重系數向量峰值位置即為HRRP強散射中心的位置,不同維度的權重系數則可以實現對HRRP角度區域的劃分。

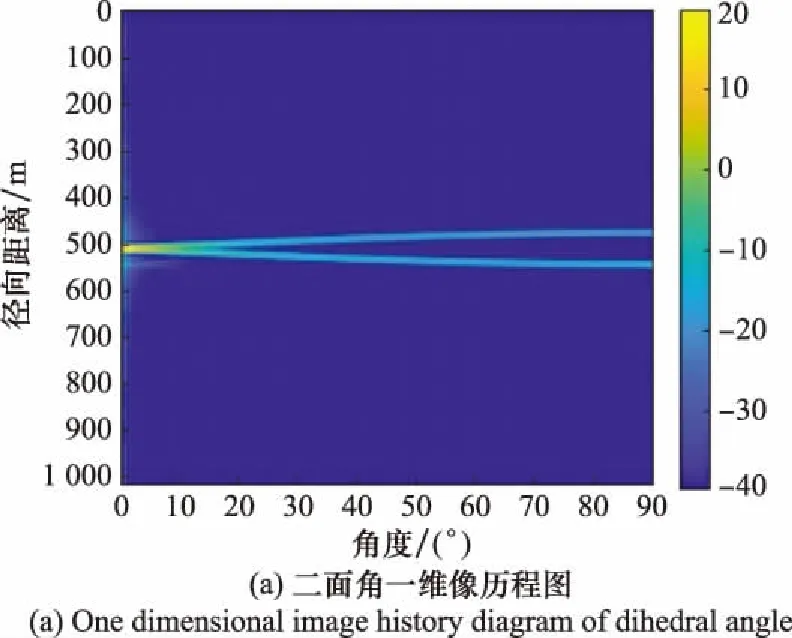
圖13 權重系數與散射中心歷程圖的對比

為進一步驗證這個結果,將傳統方法提取出的散射中心位置變化曲線與權重系數變化進行對比,如圖14所示,可以看出,不同維度的權重系數峰值對應著不同角度區域中HRRP強散射中心的位置。其中,立方體HRRP關于45°左右兩邊是對稱的,訓練完的權重系數則僅需反映對稱一側的特征變化過程。

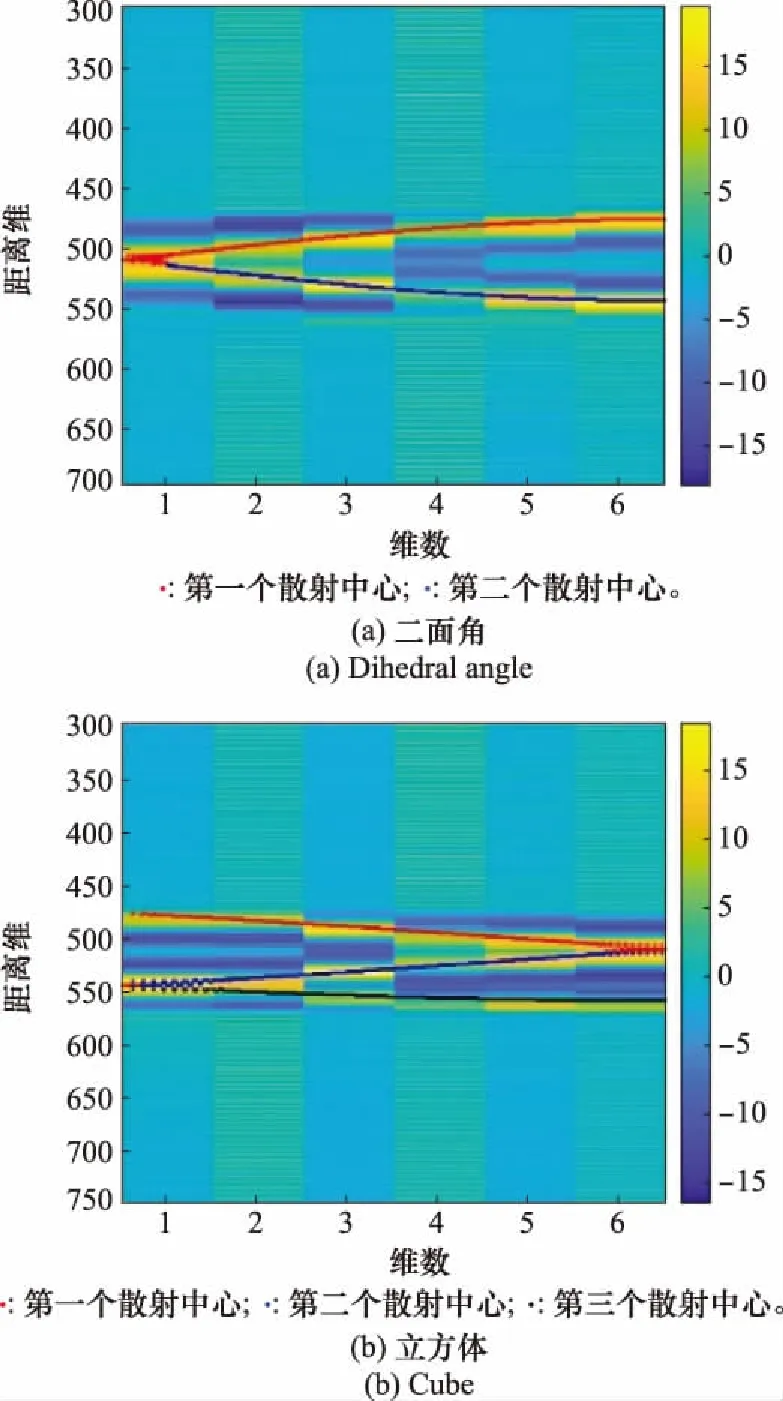
圖14 權重系數與散射中心位置特征的對比

因此,綜合權重系數矩陣W為與散射中心密切相關的類字典系數矩陣。綜合權重系數W與由式(12)定義的散射中心在距離域的字典A是相關的,但W與字典A不完全相同,字典A的每個原子只有一個散射中心,而W中與信號相關的行向量可能有多個散射中心,即它可以看成字典A的多個原子的組合,故將其稱為分子。每個分子中原子的個數與輸入HRRP數據的散射中心個數有關,從而對于每個HRRP數據只需要一個分子就可以表達,從而利用HRRP稀疏自編碼器網絡學習后,可獲得更為稀疏的表達。

3.2 降維特征與散射中心特征關聯關系

從降維后的特征圖中可以看出,降維特征能夠反映不同距離單元內散射中心強度隨角度的變化。由于第3層特征維度較少,難以直觀反映出散射中心特征的變化,因此以第一層為例開展研究。第一層特征維為256,圖15分別為二面角和三面角的第一層特征圖,三面角僅有一個強散射中心,特征圖中則可以反映出該散射中心位置和強度隨角度的變化情況,并且僅保留了散射中心相關的距離維,去除了僅有噪聲的距離維度。二面角有兩個散射中心,但是兩個散射中心是沿距離中心對稱的,因此特征圖中僅保留了一個散射中心的信息。通過上述分析可以發現,降維特征能夠實現對強散射中心的學習和提取,反映了強散射中心位置和強度隨角度的變化。從圖15中可以看出,二面角的第一層降維特征圖中提取到的散射中心在降維維數上會有展寬,這是因為二面角第一層訓練得到的權重系數W矩陣中有很多向量是冗余的,字典不夠稀疏,導致訓練完后的特征量也會存在冗余,因此不同維度的特征結果相似,導致在特征圖上會有展寬的現象。

圖15 第一層降維后特征表示

3.3 稀疏自編碼器網絡參數的影響分析

利用稀疏自編碼器對HRRP進行學習訓練和特征挖掘過程中,訓練層數和降維維數兩個參數的選擇非常重要,會直接影響訓練效果和特征的準確性。下面分析網絡訓練層數和降維維數對學習效果的影響。

(1)網絡訓練層數影響分析

利用綜合權重系數W對網絡訓練層數的影響進行分析,對比二面角和三面角的綜合權重系數W,發現二面角三層網絡的綜合權重系數能夠很好地實現方位角度區域的劃分,并準確反映散射中心的位置,而三面角的三層綜合權重系數則效果比較差,如圖16所示。再對三面角的第一層權重系數進行分析,可以看出,第一層權重系數已經能夠比較好地提取出散射中心的位置,由此可見,在學習過程中,并不是訓練層數越多越好,層數的選擇與輸入數據有很大關系。

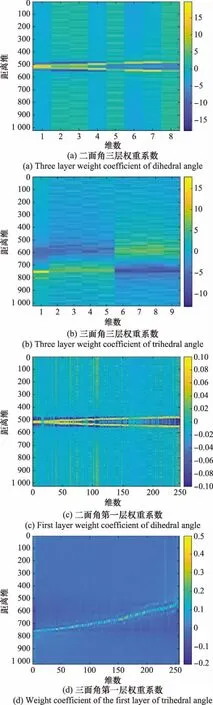
圖16 二面角與三面角權重系數比較

對比二面角和三面角HRRP歷程圖發現,三面角的散射中心距離單元變化范圍較大,而二面角的散射中心距離單元變化范圍相對較小,導致在訓練過程中,第一層訓練完之后,三面角的權重系數冗余已經很少,而二面角權重系數則存在較多的冗余。再單獨比較三面角經過兩層降到64維和僅通過一層就降到64維的結果,如圖17所示,發現單層網絡降維后的結果要好于兩層網絡。結果表明,在權重系數冗余較多時,則需要再設置新的網絡層進行訓練,而權重系數冗余較少時,則不再需要做進一步的訓練,此時單層網絡已經足夠。

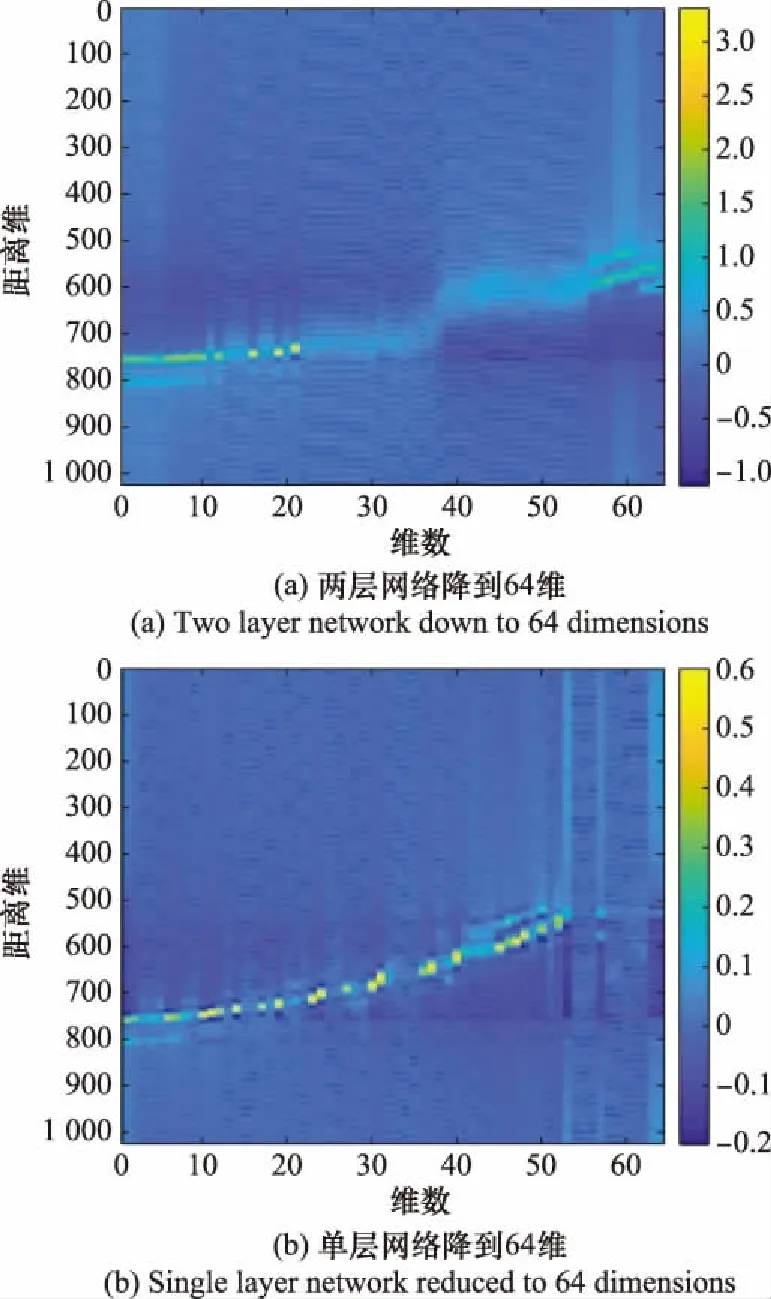
圖17 三面角單層網絡與兩層網絡的權重系數比較

(2)網絡降維維數優化選擇

利用綜合權重系數W的冗余度對降維維數的選擇進行分析,冗余度定義為冗余維度數量與總維度的比值。以二面角為例進行說明,當降維到不同維數時的冗余度如表2所示。

表2 二面角降維維數與冗余度

可以看出,同網絡層數一樣,降維維數的選擇同樣與冗余度有很大關系,二面角在維度降低到15維之前,冗余度均在50%以上,此時應該降到更低的維數,冗余度最低時對應的維數即為能夠完整表達HRRP數據的最小維數。因此,冗余度可以作為降維維數選擇的重要依據之一。

4 典型復雜體仿真驗證

上述主要針對二面角、三面角、立方體3類簡單散射結構的仿真數據而開展研究的,其結果還需要推廣到一般性復雜雷達目標去進行驗證。因此,本文還選取了MSTAR標準體SLICY目標進行了學習訓練,SLICY模型是由二面角、三面角反射器、平面、曲面、圓柱空腔、Tophat等結構復合而成的單個目標體,如圖18所示。

圖18 SLICY模型

對SLICY模型進行電磁散射特性計算,仿真條件以及入射角度定義與前面幾類標準體一樣,方位角從0°到360°,處理后一維距離像歷程圖如圖19所示,幾個強度比較大的散射中心主要由方板型三面角、三角板形三面角和圓柱頂帽等典型結構形成。利用稀疏自編碼器對SLICY模型一維距離像進行深度學習,得到第一層(降維到256)的權重系數和降維特征如圖20所示。

圖19 SLICY模型一維距離像歷程圖

圖20 SLICY模型深度學習特征

從圖20中可以看出,權重系數矩陣是可以反映強散射中心位置隨角度變化的分子集,降維特征實現了對強散射中心的學習和提取,可以反映出3～4個比較強的散射中心位置和強度隨角度的變化過程。由于SLICY模型中幾個散射中心的強度差異較大,因此第一層權重系數重點實現了對最大強度散射中心的學習訓練,基本上每個維數的分子集中僅有一個原子。訓練結果驗證了本文對于稀疏自編碼器深度網絡特征與散射中心特征之間關聯性的分析結論。

5 結 論

本文利用稀疏自編碼器網絡對典型標準體目標HRRP進行了學習訓練,并通過綜合權重系數和降維特征與散射中心位置和強度特征的對比分析,研究了稀疏自編碼器深層特征與散射中心特征之間的關聯性,對綜合權重系數和深層降維特征的物理意義進行了解釋。相關結論如下:

(1)深度學習網絡的訓練過程可以實現對方位角度區域的劃分,并可以同時實現對信號部分和噪聲部分的學習訓練;

(2)綜合權重系數矩陣為與散射中心密切相關的類字典系數矩陣,反映了強散射中心位置隨角度變化的可能的分子集;

(3)降維特征能夠實現對強散射中心的學習和提取,反映了強散射中心位置和強度隨角度的變化;

(4)散射中心沿某一角度對稱時,綜合權重系數僅需保留一半的特征,從而可以實現更低維度的降維;散射中心沿某一距離單元對稱時,降維特征只保留一半散射中心的特征,從而降低學習特征的維度;

(5)網絡層數與降維維數對訓練結果有很大的影響,當某層降維后權重系數的冗余度小于一定的值后,則不需要再增加網絡層數;降維維數與散射中心距離變化和權重系數冗余度均有關系,當散射中心距離變化緩慢并且權重系數冗余度較高時,需要減小降維的維數。

本文首次針對HRRP稀疏自編碼器網絡特征與散射中心特征的關聯性開展了深度學習特征的可解釋性研究,得到了一些初步的結論,可為后續深度學習在雷達數據處理中的廣泛應用提供有益的指導。但是仍有許多問題有待于進一步研究,如多層網絡結構中每一層特征的物理意義、網絡訓練完成后特征角度區域的自動排序、網絡層數與降維維數等參數的具體優化選擇方法、稀疏自編碼器在散射中心頻率特征提取中的應用等等,后續還將加強深度學習網絡在電磁散射特征提取與識別中的應用研究,為雷達目標的智能識別提供更有效的工具。