基于幾何精度稀釋的矢量潛標最優布站

丁 超, 戴衛國,*, 王 森, 程玉勝

(1.海軍潛艇學院航海觀通系, 山東 青島 266000; 2.中國人民解放軍91154部隊, 海南 三亞 572000)

0 引 言

矢量潛標能夠獲得同時共點的聲壓信息與多路振速信息[1-2],組陣之后,既能獲得更高的信噪比,也能適用多種定位算法,因而在水聲目標被動定位中具備了諸多優勢。被動定位方法按照定位體制與測量類型主要可以分為以下幾類:基于到達方向(direction of arrival,DOA)[3-6]、基于到達時差(time difference of arrival,TDOA)[7-10]、基于到達頻差[11]、基于多普勒變化率[12]、基于相位差變化率以及聯合定位方法[13-16]等。

在以上方法之中,到達頻差、多普勒變化率、相位差變化率等的測量估算,需要目標與觀測平臺之間有較快的相對運動速度,并且需要定位系統對目標運動信息有一個較為準確的估計[17],并不適用于潛標環境。基于DOA的定位方法原理簡單、易于實現,是最為常用的目標定位方法之一;基于TDOA的定位方法結果穩健、抗噪性好,對遠距離目標有一定的定位能力。因此,二者成為矢量潛標陣列的常用定位方法,結合兩種算法的矢量潛標陣列定位能力分析具有更好的普適性。考慮到聲線彎曲、多途效應等復雜海洋信道情況,本文DOA定位與TDOA定位均在二維平面進行。

矢量潛標陣列水聲目標被動定位精度受多種因素綜合影響,除去海洋信道環境等外界因素干擾、聲納探測性能等硬件設備影響,在信號處理方法確定的情況下,從布陣角度分析[18-19],提高陣列定位精度的途徑可以分為兩類:增加陣元數量和優化布站幾何。本文對矢量潛標陣列兩種被動定位算法進行簡要介紹,并結合具體定位算法,針對陣元數量和布站幾何展開分析研究,以求獲得矢量潛標陣列的最優布站。

1 定位原理及性能度量方法

定位誤差大小是衡量定位系統性能的重要指標。常用的定位誤差描述和度量方法有:均方誤差、均方根誤差、圓概率誤差、克拉美羅下界以及幾何精度稀釋(geometrical dilution of precision, GDOP)等[20-26]。其中,GDOP是一種十分常用的定位誤差評估方法[27-30],能夠以等高線圖形式直觀形象地表示出定位系統在不同空間位置的定位誤差大小,某點處值越小表示該處定位精度越高,方便對不同定位系統的性能進行比較。本文選用GDOP來對矢量潛標陣列定位能力進行度量。

1.1 DOA定位

兩枚矢量潛標可以獲取兩個方位信息,兩條非平行方位線交叉可以獲取目標位置。實際情況中,陣元可能多于兩個。假定聲源位置T(x,y)未知,第i號陣元位置為Si(xi,yi),易得幾何關系如下:

(1)

式中：θi為目標輻射噪聲到達陣元Si的方位；N為陣元數量。

對式(1)進行全微分,整理可得

(2)

將式(2)整理成矩陣形式:

dD=GdT+dS

(3)

式中：dD=[dθ1,dθ2,…,dθN]T為測向誤差,其中

為轉移矩陣；dT=[dx,dy]T為定位誤差；

為站址誤差。

由偽逆法可得定位誤差為

dT=(GTG)-1GT(dD-dS)=A(dD-dS)

(4)

則定位誤差協方差矩陣為

PdT=E{dTdTT}=A{E[dDdDT]+E[dSdST]}AT

(5)

則DOA定位誤差GDOP為

(6)

1.2 TDOA定位

三枚矢量潛標可以獲取兩組時延信息,每組時延信息可以確定一條雙曲線,兩條雙曲線交匯可以獲取目標位置。實際情況中,陣元可能多于3個。假定聲源位置T(x,y)未知,主站位置為S0(x0,y0),第i號副站位置為Si(xi,yi),易得幾何關系如下:

(7)

式中：c為海洋聲速；τi為目標輻射噪聲到達陣元Si的用時；N為副站數量。

水聲目標被動定位中,τi無法直接獲得,但其差值可以通過時延估計求得

(8)

對式(8)進行全微分,整理可得

(9)

將式(9)整理成矩陣形式:

dR=HdT+dS

(10)

式中：dR=[dΔr1,…,dΔrN]T為聲程差估計誤差；

為轉移矩陣；dT=[dx,dy]T為定位誤差；

為站址誤差。

由偽逆法可得定位誤差為

dT=(HTH)-1HT(dR-dS)=B(dR-dS)

(11)

則定位誤差協方差矩陣為

PdT=E[dTdTT]=B{E[dRdRT]+E[dSdST]}BT

(12)

則TDOA定位誤差GDOP為

(13)

2 矢量潛標陣列實際應用需求

矢量潛標陣列在實際應用中有以下需求:

(1)潛標布放海域,缺乏目標位置、航向、航速等先驗知識,陣列需要具備全向探測能力;

(2)潛標陣列宜適用于多種算法,以便提高定位精度;

(3)綜合考慮工程實現難度及布放成本、計算成本等問題,潛標數量不宜過多、陣列結構不宜復雜;

(4)矢量潛標陣列的主要目的在于警戒,故宜少枚多組,而非一組多枚。

陣列拓撲結構可以分為線型、面型(包括非中心型結構和中心型結構)、球型3大類,依次如圖1所示。

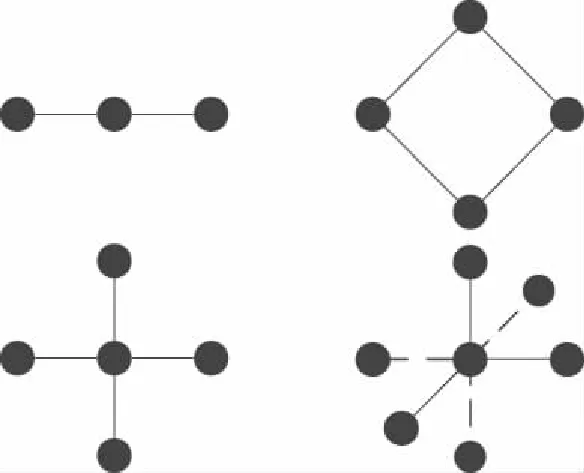
圖1 陣列拓撲結構

線型結構構造簡單、信號處理簡便,但其定位盲區過大,不適用于潛標環境;球型結構在海洋中布放十分困難,且系泊系統運動的不穩定性會導致定位誤差增大[31],同樣不適用于潛標環境。

綜合以上,矢量潛標陣列宜選用呈旋轉對稱的面型拓撲結構,陣元數量三枚至多枚。

3 矢量潛標陣列陣元數量研究

呈旋轉對稱的面形拓撲結構可看作是均勻圓陣,分為無圓心均勻圓陣與有圓心均勻圓陣兩類。本節將對三至八元無圓心和有圓心均勻圓陣的GDOP分布進行計算并比較分析,以確定陣元數量對定位精度的影響。不妨定義GDOP值小于500的區域為高定位精度區域,以其面積大小反映某算法下某陣列的定位精度。由于等高線圖形狀的不規則性,本文將GDOP圖劃分為足夠細小的單元,使用統計法計算等高線內面積。

3.1 陣元數量對定位精度的影響

為比較陣元數量對DOA定位精度的影響,控制陣列半徑、測量誤差、站址誤差等因素不變,比較不同陣元數量的陣列GDOP分布。

3.1.1 陣元數量對DOA定位精度的影響

設置仿真條件如下:陣列幾何中心位于原點,陣列半徑500 m,測向誤差標準差均為0.2°,之間相關系數為0,無站址誤差。以三元、四元陣為例,其DOA定位GDOP分布如圖2所示,其中,紅色圓點為陣元位置,4條等高線值由小至大分別為500,1 000,2 000,5 000。

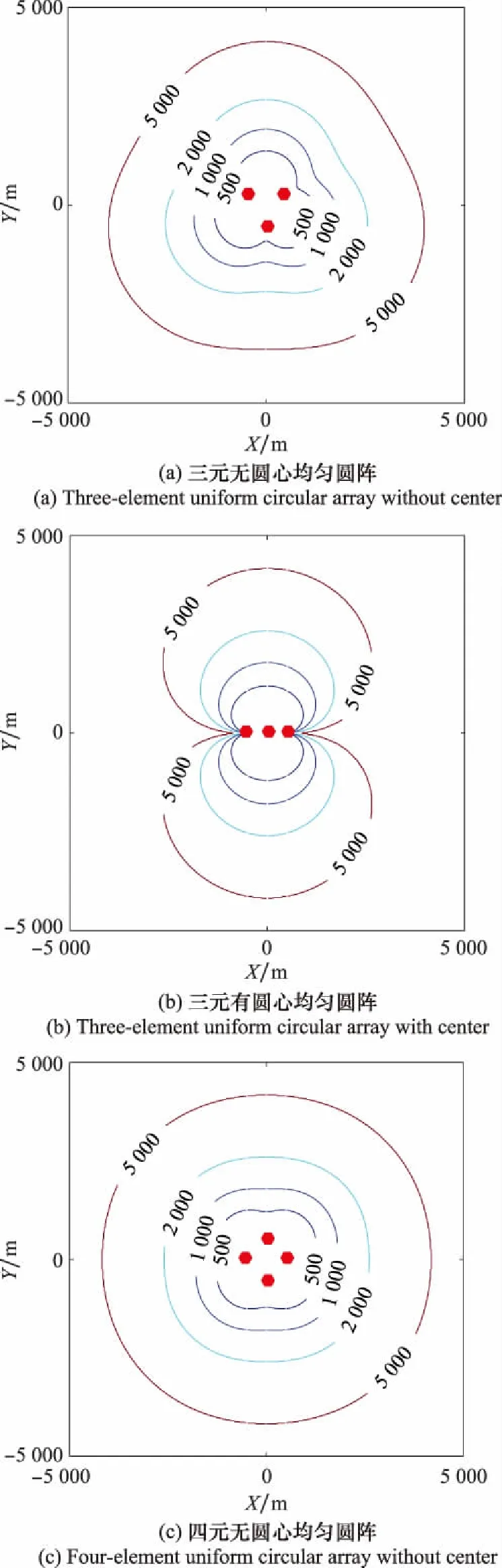
圖2 DOA定位GDOP

比較兩種類型圓陣DOA定位的高定位精度面積,結果如圖3所示。

圖3 陣元數量對DOA定位影響

通過對比分析,可以得到以下結論:

(1)三元有圓心均勻圓陣(即線陣)存在嚴重的DOA定位盲區;

(2)隨著陣元數量增加,陣列DOA定位精度逐漸提高,但提高速度越來越慢,故增加陣元的性價比將隨著陣元數量增多而降低。

3.1.2 陣元數量對TDOA定位精度的影響

設置仿真條件如下:陣列幾何中心位于原點,陣列半徑500 m,時延誤差標準差均為0.03 s,之間相關系數為0,聲速為1 500 m/s,無站址誤差。以三元、四元陣為例,其TDOA定位GDOP分布如圖4所示。其中,藍色圓點為主站位置,紅色圓點為副站位置,4條等高線值由小至大分別為5 00,10 00,2 000,5 000。

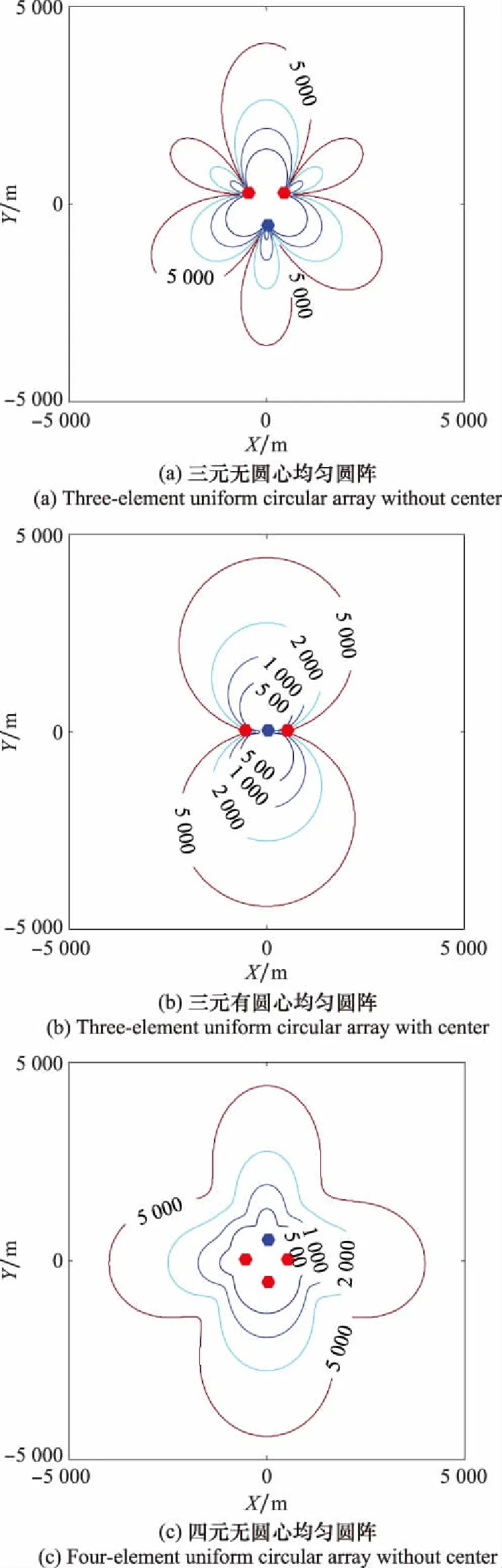
圖4 TDOA定位GDOP

比較兩種類型圓陣TDOA定位的高定位精度面積,結果如圖5所示。

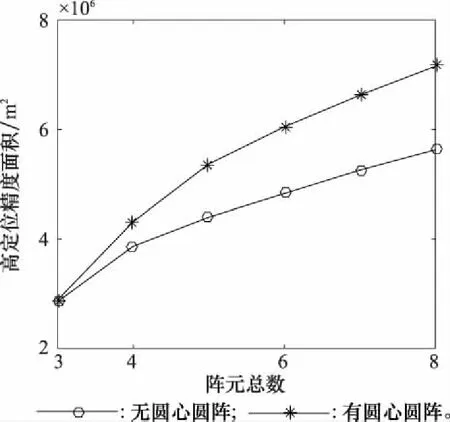
圖5 陣元數量對TDOA定位的影響

通過對比分析,可以得到以下結論:

(1)三元無圓心均勻圓陣及有圓心均勻圓陣均存在嚴重的TDOA定位盲區;

(2)隨著陣元數量增加,陣列TDOA定位精度逐漸提高,但提高速度越來越慢,故增加陣元的性價比將隨著陣元數量增多而降低。

3.2 潛標陣列陣元數量選擇

參與定位的陣元數目對定位精度有很大影響,陣元數目越多,獲取到的待測目標信息越豐富,通過冗余信息處理所獲取的目標位置也就越精確;同時,陣列定位精度與其空間結構緊密相關,陣元數目越多,陣型結構可以設計的越復雜,其全向定位能力也就相對越好。

當然,陣元數目也并非越多越有利。除去經濟因素之外,首先,隨著陣元數量增加,潛標陣列布放難度將急劇增加;其次,隨著冗余信息增加,計算復雜度和運算量將大大增加,信息利用的充分性和定位結果的實時性將難以得到保證。

結合上文計算分析及實際使用經驗,矢量潛標陣列具有以下特點:

(1)矢量潛標陣列想要兼顧DOA定位與TDOA定位,至少需要3個陣元,若考慮到潛標損壞替補等特殊情況,需要4個以上陣元;

(2)三陣元時所存在的嚴重的定位盲區,在四陣元以上時會被極大消除,故四陣元是矢量潛標陣列定位性能的質變點;

(3)隨著陣元數量增加,陣列定位精度提升越來越少,工程實現難度及布放成本、計算成本卻急速升高,故陣元數不宜過多;

(4)在滿足基本需要的基礎上,應減少單組潛標數量,增加潛標陣列組數,從而覆蓋更大的警戒海域。

綜合考慮,本文認為四陣元是潛標陣列定位性能的質變點,也是性價比的最高點,既能夠應對功能需求,也較為符合工程實際,故四元旋轉對稱面陣是潛標陣列的較優選擇。

4 矢量潛標陣列布站幾何研究

除陣元數量外,布陣幾何也是影響矢量潛標陣列定位精度的關鍵要素。被動定位方法研究最重要的目的就是減小定位誤差、提高定位精度,對比不同陣型在不同陣列半徑、測量誤差、站址誤差下的定位精度,對于陣列最優布站具有指導意義。

四元旋轉對稱圓陣包含非中心陣結構的四元十字陣和中心陣結構的四元Y型陣,如圖2和圖4中的四元陣。設置參數如下:陣列半徑500 m,無站址誤差。測向誤差標準差均為0.2°,之間相關系數為0;時延誤差標準差均為0.03 s,之間相關系數為0,聲速為1 500 m/s。分別計算DOA定位算法和TDOA定位算法下的四元十字陣和四元Y型陣的GDOP分布。以GDOP值為橫坐標,統計該GDOP值等高線內得面積,結果如圖6所示。

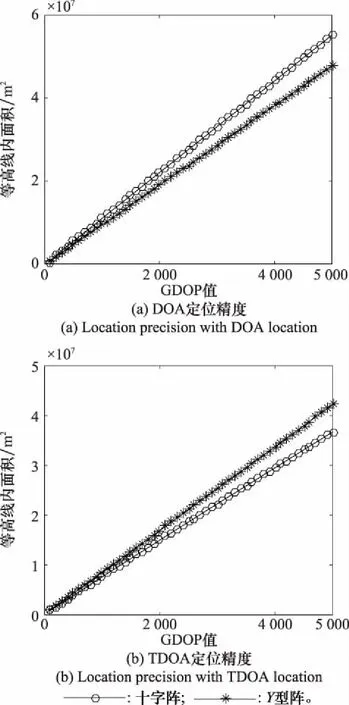
圖6 兩種陣型定位精度對比

可以發現:① 四元十字陣有更好的DOA定位精度,四元Y型陣有更好的TDOA定位精度,但總體來說,二者相差不大;② 兩種陣型、兩種算法的GDOP分布中,某等高線內面積與該等高線值基本成正比,故GDOP圖中某等高線內面積的變化規律即能反應定位精度的整體變化規律。

4.1 陣列半徑敏感度對比

陣列半徑是陣列設計的重要參數,能夠直接影響到陣列的定位精度、覆蓋范圍等。

4.1.1 DOA定位陣列半徑敏感度對比

設置仿真條件如下:測向誤差標準差均為0.2°,之間相關系數為0,無站址誤差。控制陣列半徑從100 m增加至1 000 m,求取兩陣型DOA定位的GDOP,并計算高定位精度區域面積,結果如圖7和表1所示。

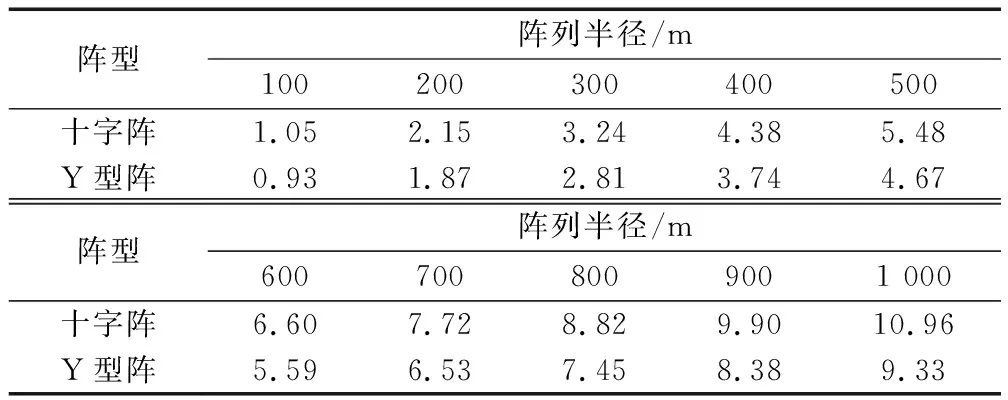
表1 DOA定位陣列半徑敏感度

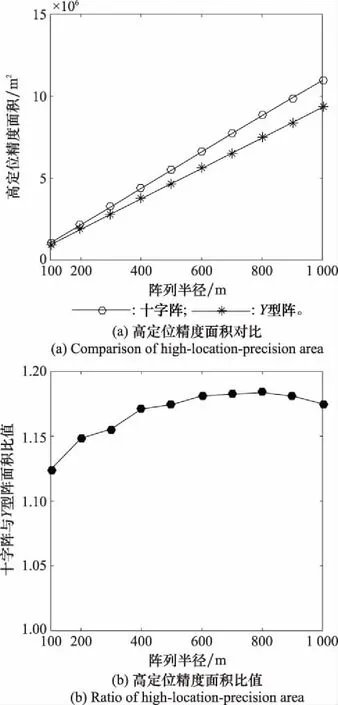
圖7 DOA定位陣列半徑敏感度

4.1.2 TDOA定位陣列半徑敏感度對比

設置仿真條件如下:時延誤差標準差均為0.03 s,之間相關系數為0,聲速為1 500 m/s,無站址誤差。控制陣列半徑從100 m增加至1 000 m,求取兩陣型TDOA定位的GDOP,并計算高定位精度區域面積,結果如圖8和表2所示。

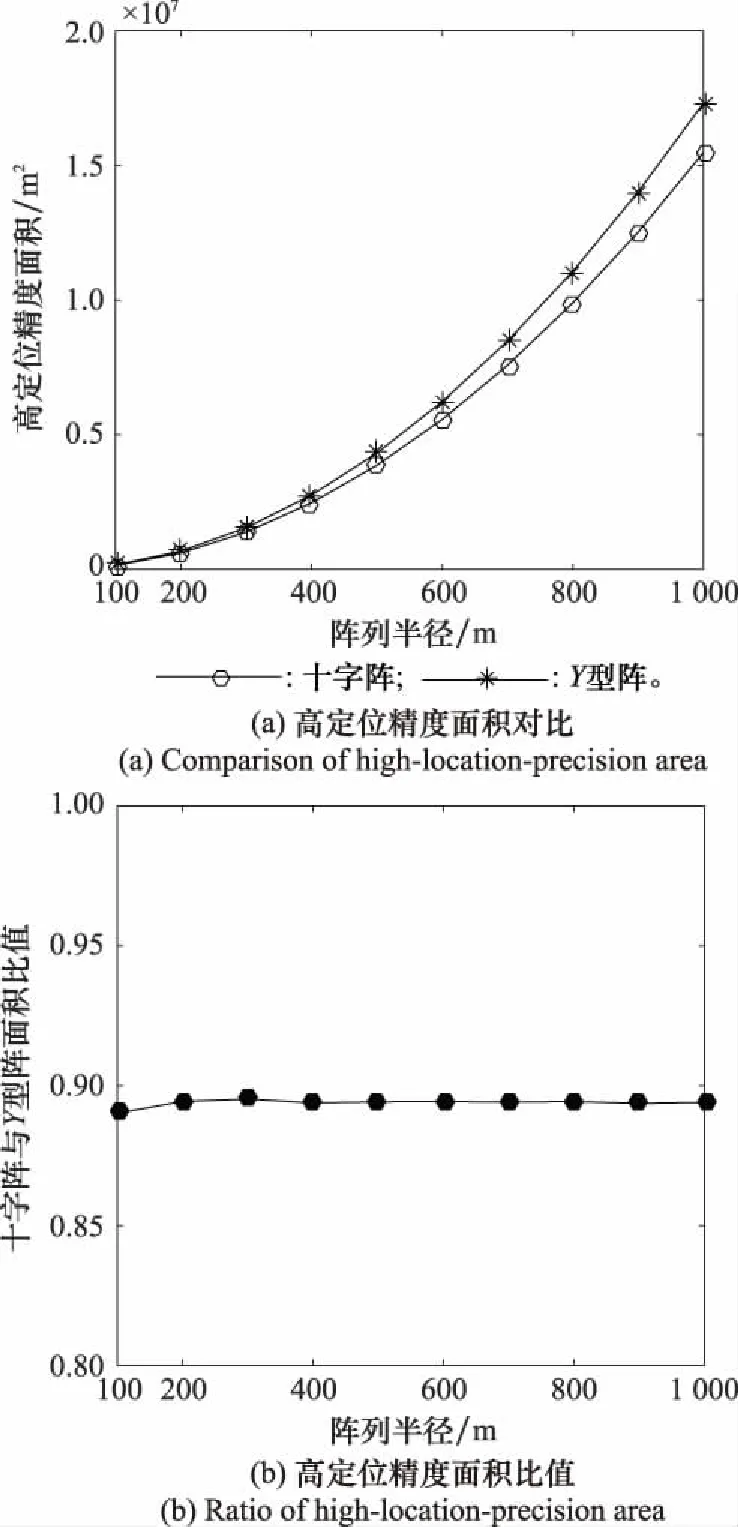
圖8 TDOA定位陣列半徑敏感度

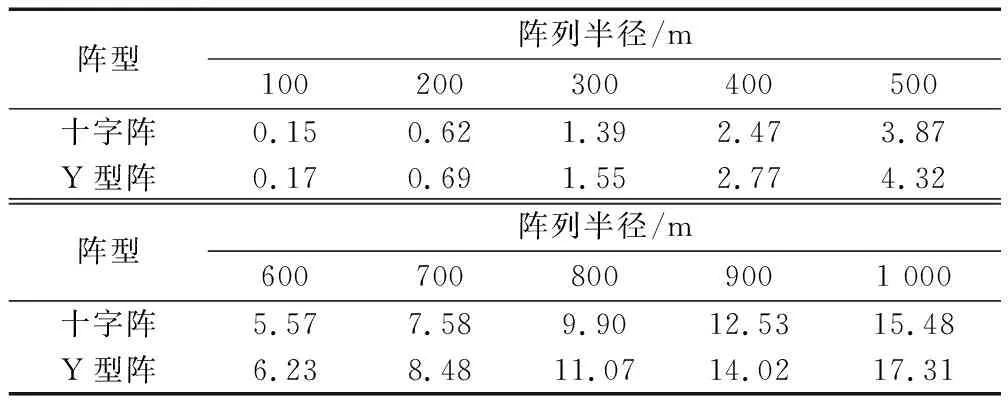
表2 TDOA定位陣列半徑敏感度

通過仿真對比可以發現,DOA定位方法中,兩種陣型的高定位精度面積與陣列半徑基本呈一次函數關系;TDOA定位方法中,兩種陣型的高定位精度面積與陣列半徑基本呈二次函數關系。但在半徑1 000 m范圍內,同算法下,兩種陣型高定位精度面積相差不大。

在實際應用中,處理相關信號時,陣列中兩陣元間距應小于空間相關半徑。實驗證明空間相關半徑約為300～500λ,其中λ為信號波長[32]。考慮到通常的信號頻率范圍,潛標的空間相關半徑不會太大,故同算法下,兩種陣型定位精度相差不大。

4.2 測量誤差敏感度對比

在陣型確定的情況下,測量誤差會對定位結果產生很大影響,受測量誤差影響小的陣型,即抗噪能力強的陣型具有更高的實用價值。

4.2.1 DOA定位測量誤差敏感度對比

設置仿真條件如下:陣列半徑500 m,無站址誤差。控制測向誤差標準差從0.1°逐漸增加到1°,之間相關系數為0,求取兩陣型DOA定位的GDOP,并計算高定位精度區域面積,結果如圖9和表3所示。

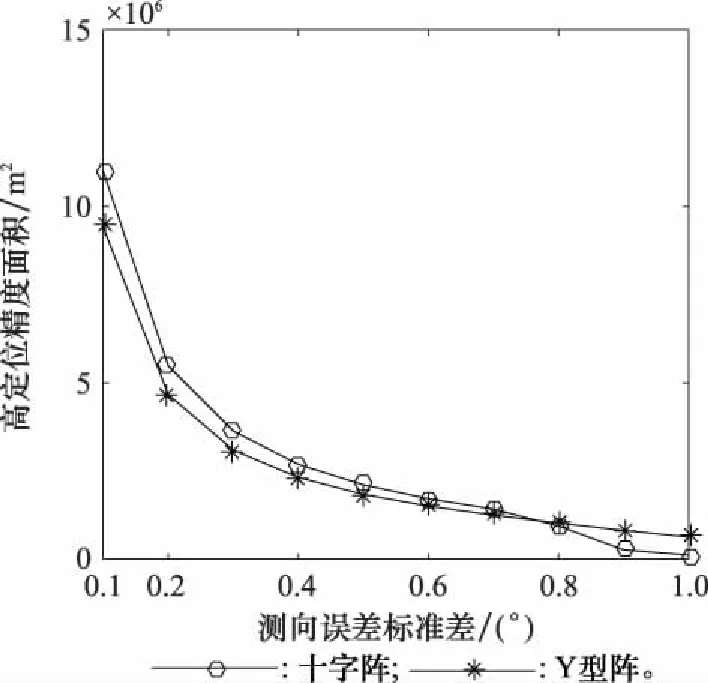
圖9 DOA定位測量誤差敏感度

表3 DOA定位測量誤差敏感度

4.2.2 TDOA定位測量誤差敏感度對比

設置仿真條件如下:陣列半徑500 m,無站址誤差。控制時延估計誤差標準差從0.01 s逐漸增加到0.1 s,之間相關系數為0,聲速為1 500 m/s,求取兩陣型TDOA定位的GDOP,并計算高定位精度區域面積,結果如圖10和表4所示。

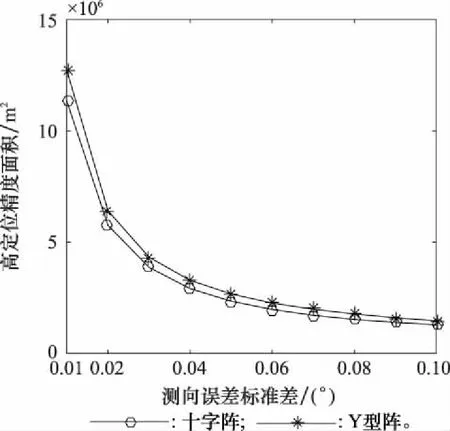
圖10 TDOA定位測量誤差敏感度

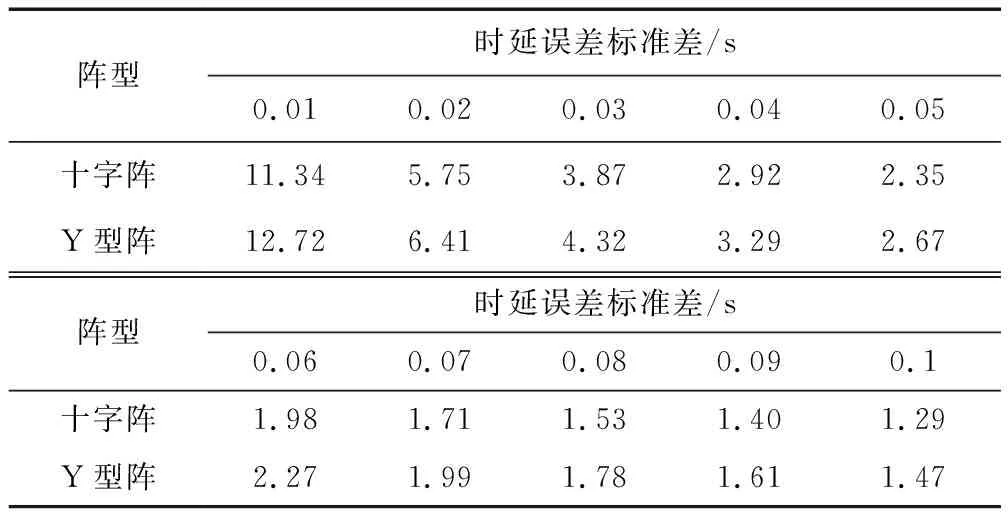
表4 TDOA定位測量誤差敏感度

通過仿真對比可以發現,DOA定位方法中,四元Y型陣抗測量誤差能力強于四元十字陣。隨著測向誤差的增加,四元Y型陣定位精度逐漸超過四元十字陣,即四元Y型陣更為可靠,更適用于復雜多變的海洋環境;TDOA定位方法中,四元Y型陣與四元十字陣的抗測量誤差能力基本持平,但四元Y型陣定位精度始終優于四元十字陣。

4.3 站址誤差敏感度對比

在實際應用中,站址誤差不可避免,會對目標定位精度產生直接影響,抗站址誤差能力強的陣型對工程實現有更好的寬容度。

4.3.1 DOA定位站址誤差敏感度對比

設置仿真條件如下:陣列半徑500 m,測向誤差標準差均為0.2°,之間相關系數為0。控制站址誤差從0 m逐漸增加到18 m,求取兩陣型DOA定位的GDOP,并計算高定位精度區域面積,結果如圖11和表5所示。

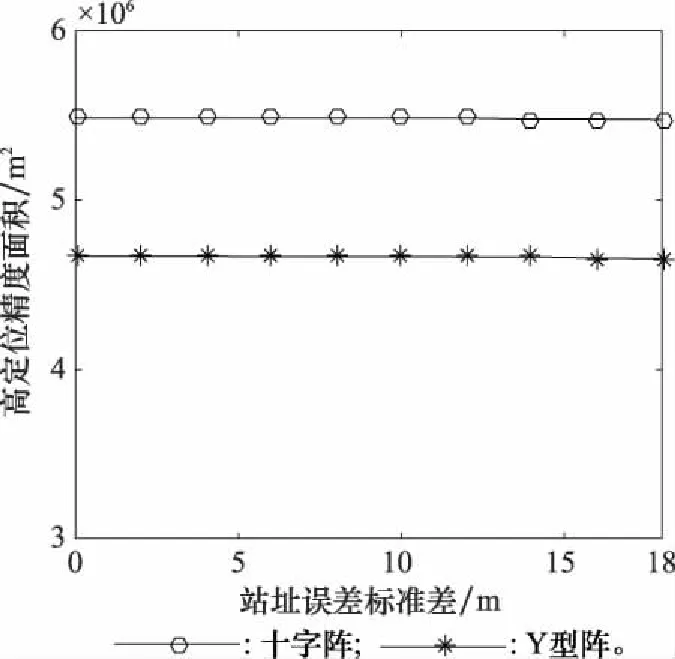
圖11 DOA定位站址誤差敏感度

表5 DOA定位站址誤差敏感度

4.3.2 TDOA定位站址誤差敏感度對比

設置仿真條件如下:陣列半徑500 m,時延誤差標準差均為0.03 s,之間相關系數為0,聲速為1 500 m/s。控制站址誤差從0 m逐漸增加到18 m,求取兩陣型TDOA定位的GDOP,并計算高定位精度區域面積,結果如圖12和表6所示。

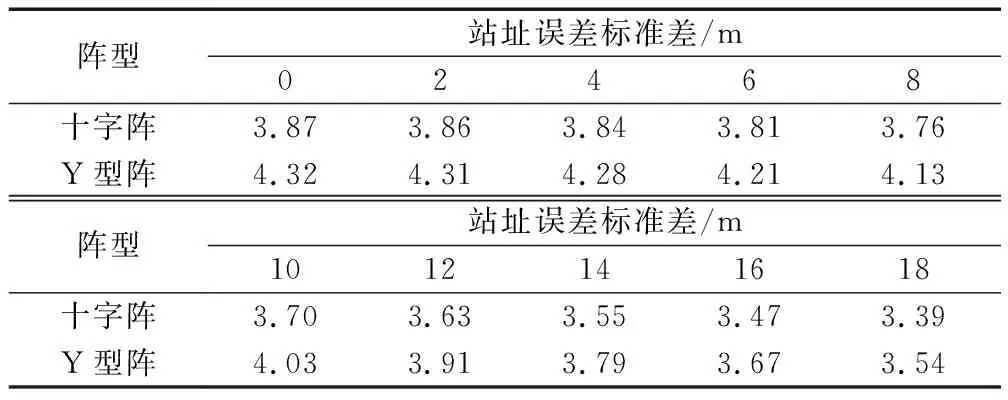
表6 TDOA定位站址誤差敏感度

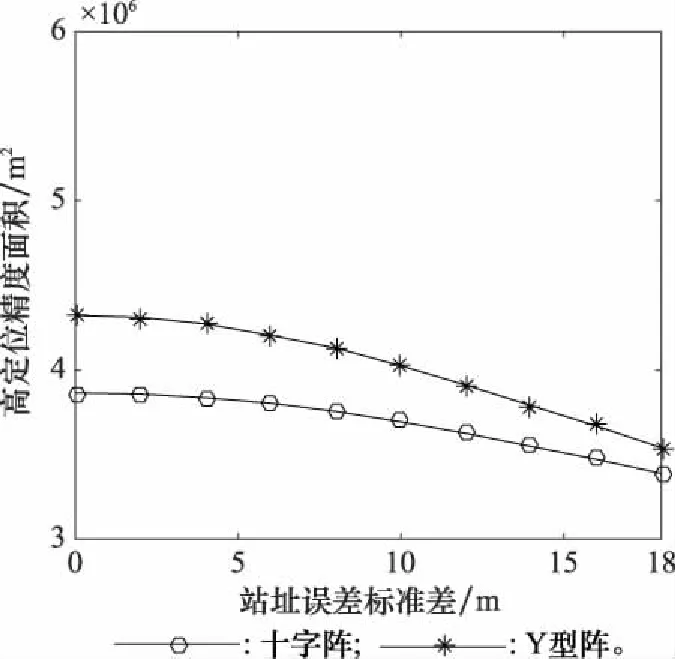
圖12 TDOA定位站址誤差敏感度

通過仿真對比可以發現,DOA定位方法抗站址誤差能力較強,且在DOA定位方法中,兩陣型抗站址誤差能力基本持平;TDOA定位方法抗站址誤差能力相對較弱,在TDOA定位方法中,四元Y型陣抗站址誤差能力略遜于四元十字陣。

4.4 相關半徑約束下陣列最大半徑對比

在相關半徑約束下,保證所有副站都在主站相關半徑內時,不同陣列結構所能獲得的最大陣列半徑亦不相同。具體到四元十字陣和四元Y型陣,當相關半徑為R時,在保證所有副站都在主站相關半徑內時,四元十字陣最大陣列半徑為R/2,四元Y型陣最大陣列半徑為R。

設置仿真條件如下:測向誤差標準差均為0.2°,之間相關系數為0;時延誤差標準差均為0.03 s,之間相關系數為0,聲速為1 500 m/s,無站址誤差。控制相關半徑從200 m增加至1 000 m,求取兩陣型的最大陣列半徑,并求取最大陣列半徑下DOA定位和TDOA定位的GDOP高定位精度區域面積,結果如圖13和圖14所示。

圖13 相關半徑約束下DOA定位精度對比

圖14 相關半徑約束下TDOA定位精度對比

通過計算對比可以發現,相同相關半徑約束下取最大陣列半徑時,四元Y型陣的DOA定位精度和TDOA定位精度均遠高于四元十字陣,且相關半徑越大差距越大。

4.5 陣元覆蓋面積對比

前文可知,DOA定位至少需要兩個陣元,TDOA定位至少需要3個陣元,當具備4個陣元以上時,陣列定位性能將得到較大提高,且可輔助消除定位模糊。也就是說,陣元覆蓋范圍直接決定了陣列的有效作用范圍。假定潛標陣列半徑500 m,潛標有效探測范圍半徑5 000 m,可以求得陣列的三陣元覆蓋范圍及四陣元覆蓋范圍,如圖15所示。

圖15 陣元覆蓋范圍示意圖

圖15中,紅點表示陣元位置,顏色越亮的區域覆蓋陣元越多,明黃色為四陣元覆蓋區,暗黃色為三陣元覆蓋區。不同陣列半徑下,三陣元及四陣元的覆蓋面積,如圖16所示。通過計算對比可以發現,相同陣列半徑時,四元Y型陣的三陣元覆蓋面積及四陣元覆蓋面積均大于四元十字陣,且隨著陣列半徑增加,差距越來越大。

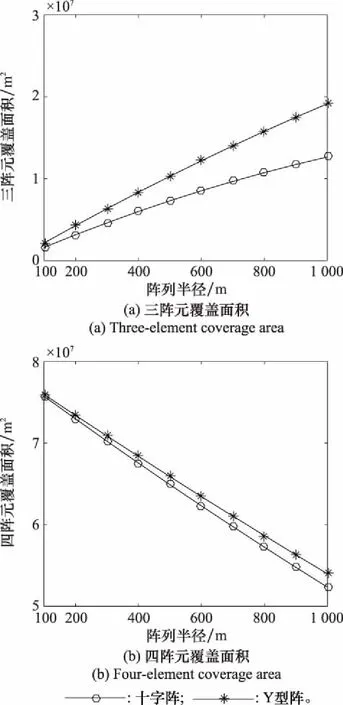
圖16 陣元覆蓋范圍對比

4.6 矢量潛標陣列布站幾何選擇

通過對四元十字陣和四元Y型陣陣列半徑敏感度、測量誤差敏感度、站址誤差敏感度、陣元覆蓋面積等的全面對比,可以得出以下結論:

(1)同條件下,四元十字陣的DOA定位精度略高于四元Y型陣,四元Y型陣的TDOA定位精度略高于四元十字陣;

但由于DOA定位性能會隨目標距離增加急劇下降,在實際應用中通常作為輔助定位方法,而將TDOA定位方法作為主要定位手段,故四元Y型陣更具實用性;

(2)同條件下,四元Y型陣具有更好的抗測向誤差能力,因為能夠更好地應對復雜的海洋環境;

(3)同條件下,DOA定位時兩種陣型抗站址誤差能力基本持平;TDOA定位時四元Y型陣抗站址誤差能力略遜于四元十字陣,但在實際情況下,Y型陣的TDOA定位能力仍強于十字陣;

(4)相同相關半徑約束下取最大陣列半徑時,四元Y型陣的DOA定位精度和TDOA定位精度均遠高于四元十字陣;

(5)相同陣列半徑時,四元Y型陣的三陣元及四陣元覆蓋面積均大于四元十字陣;

(6)就兩種陣型的GDOP圖等高線形狀而言,四元Y型陣無論DOA定位還是TDOA定位,各方位定位能力均較均衡;而四元十字陣在TDOA定位時各方位定位能力存在嚴重的不均衡性。

綜合考慮,本文認為四元Y型陣具有更穩健的定位性能,更適合于矢量潛標陣列的實際應用環境。

5 結 論

除海洋環境和潛標性能外,陣元數量和布站幾何是影響矢量潛標陣列定位精度的關鍵要素。結合實際需求,通過理論推導及仿真證明,本文得出以下結論:

(1)旋轉對稱面陣具備較好的全向探測能力,且便于在復雜海洋環境下工程實現,在幾種陣型中最能夠滿足潛標陣列的警戒需求;

(2)四元潛標陣列極大消除了三元潛標陣列的定位盲區,是潛標陣列定位能力的質變點,也是性價比的最高點,考慮到警戒聲納宜少枚多組以擴大覆蓋海域的需求特點,四元陣列是矢量潛標陣列的最優選擇;

(3)四元旋轉對稱面陣包含四元十字陣及四元Y型陣兩種,其中,四元Y型陣在同等條件下,具備更高的TDOA定位精度、更高的抗測量誤差能力、更大的有效作用范圍,同時抗站址誤差能力也沒有短板,更加適用于矢量潛標陣列。

綜合考慮,成旋轉對稱的四元Y型陣是基于GDOP衡量標準的矢量潛標陣列的最優布站。