基于順次分配機制的無人裝備體系架構方案空間搜索方法
周 鑫, 王維平, 朱一凡, 王 濤, 井 田
(國防科技大學系統工程學院, 湖南 長沙 410073)
0 引 言
當前戰爭越來越復雜,裝備之間的聯系愈加多樣,特別是近些年無人裝備[1-3]的逐漸使用,使得作戰樣式發生深刻變化。體系是有限數量組分系統的集成,這些組分系統能夠獨立運行,在一定時間段內相互聯系以實現更高的目標[4-6]。無人裝備體系是以無人裝備為核心的體系,是由協同網絡連接的無人裝備系統組成,這些無人裝備系統具有某些性能上互補的功能,可以完成某些任務,其核心要素是使命任務、裝備系統和交互協同。從功能結構可以劃分為偵察監視預警無人裝備體系、指揮控制無人裝備體系、火力打擊無人裝備體系和綜合保障無人裝備體系;從對象層次分可以分為無人裝備編制體系、面向任務的無人裝備體系等。本文主要研究面向任務的無人裝備體系(本文中簡稱裝備體系),由于裝備體系是復雜的,涉及到裝備建設與應用的諸多方面,因此本文通過研究裝備體系架構來研究整個體系。架構[7-8]是體系的組分系統、組分系統之間關系,以及約束其演化的規則和指南。當前面向任務的裝備體系架構少有從影響作戰能力的核心要素出發進行考量,同時往往直接給出了架構與能力之間的映射關系。然而很多情況下,能力與架構之間難以找到映射關系,更有可能是一種概率關系。因此,本文定義了裝備體系架構形式化模型框架,構建了架構方案空間搜索問題模型,并提出了一種動態規劃算法以求解問題。
與指導建筑施工的架構圖一樣,裝備體系架構也用于指導裝備體系的建設與運用。面向不同使命和環境,不同裝備體系表現出不同的能力,該體系是基于架構構建的,因而可以認為每個架構具有潛在的能力,稱為架構能力。需要說明的是,架構能力在體系建成之前是不確定的。所謂原型化,就是將邏輯層面的架構實例化為物理層面的體系的過程,例如搭建仿真系統、演示系統、實物系統等。在設計架構一般考慮體系的核心要素,無法考慮所有可能要素。因此,架構能力的不確定性體現在兩個方面:架構本身的性質,設計過程中未考慮的一些次要因素。其次,可能存在多種手段將同一種架構原型化為體系。此時,應評估這些手段的預期收益以便做出最佳選擇。再者,可能需要若干備選架構以便供決策者選擇。
鑒于此,本文主要工作如下:第一,提出了一種裝備體系架構超網絡模型,該超網絡主要由任務網絡、裝備網絡、協同網絡組成,此外提出了一種新穎的架構方案空間動態規劃問題框架[9]。第二,針對架構方案空間動態規劃問題,論文提出了一種基于順次分配的多Agent搜索算法,從理論上分析了該算法具有多項式時間的計算復雜度,并且可能是最優的。第三,論文通過仿真實驗檢驗和評估了算法的性能,實驗結果表明提出的算法質量很好,并優于其他基準算法。
1 相關工作
本節從裝備體系架構和架構搜索問題兩方面回顧有關相關工作。
1.1 裝備體系架構
能力是在一定預先籌備和環境條件的前提下,完成作戰使命以達到某些作戰效果[10-11]。美國國防部認為生成作戰能力需要提高理論、組織、訓練、裝備、領導和教育、人員、設施和政策[12-13]幾個方面水平,即將裝備和非裝備要素有機地結合在一起[14-15]。本文著重從裝備角度出發設計滿足作戰能力的體系。目前,許多學者對裝備體系架構提出了自己的理解,但沒有統一的概念。在軍事應用中,許多體系架構框架被廣泛使用。常見的架構建模框架包括:美國國防部體系結構框架[16]、英國國防部體系架構框架[17]、北約體系架構框架[18]。本質上這些架構可以由超網絡模型表示,超網絡是指規模龐大、連接復雜、節點異構的網絡,即超網絡由多個不同特征的網絡組成,這些網絡具有多層、多維、多屬性等特征。超網絡是一種通用模型,可用于反映裝備體系架構中的相互作用關系。例如,Gao[19]提出了一種超網絡模型,包括感知節點、指控節點和打擊節點,以及這些節點之間的關聯。Shi[20]提出了一種由5個異構節點組成的超級網絡,包括傳感器節點、信息節點、決策節點、通信節點和交戰節點,節點之間存在不同類型的交互。Chen[21]提出了一種指控超網絡模型,包括感知子網、指控子網和火力子網。不同于與之前提出的超網絡模型,本文面向任務能力的核心要素,即任務、提煉體系架構,并給出超網絡模型形式化描述。本文工作與現有工作出發點不同,之前研究出發點是作戰過程中主要環節。而本文的出發點是基于能力,衡量架構優劣的指標也是能力。
基于能力的架構設計考慮了在近期和遠期可能遇到的不同威脅,以及在軍事上要消除這種威脅所需要的能力,更多著眼于對手當前和未來可能怎么打仗。該模式具有更為廣泛的視野,更具有指導性和目標性。關于架構能力與架構超網絡模型之間的關系,之前研究者大多將其建模為函數關系,如Shu[11]提出了架構超網絡模型與架構能力之間的映射關系,并提出了一種基于智能演化的架構方案空間探索算法。然而能力與架構之間往往難以給出映射關系,因為還涉及到許多不確定因素,因此兩者之間更有可能是符合概率關系。
1.2 方案空間搜索
在本文中,裝備體系架構被建模為一個超網絡方案,面向同一使命任務的多個超網絡方案構成了體系架構空間。那么,此時需要提出架構空間搜索算法以便從中選擇最優的若干架構方案。本文將架構方案空間搜索問題建模為一類數學優化問題,并將架構方案空間搜索問題轉換為一種方案路徑選擇問題,這問題類似于旅行商問題[22]。旅行商問題是一個組合優化問題,是指推銷員遍歷所有城市并返回其家鄉城市的最短行程,期間不能兩次訪問同一城市。旅行商問題被廣泛用于實際問題中,例如車輛路線規劃和倉庫貨物放置[23-24]。群體智能算法是解決組合優化問題的有效手段,例如遺傳算法、粒子群算法、蟻群算法、螢火蟲算法、蝙蝠算法、細菌菌落覓食算法、蜂群算法和蜘蛛猴算法,以及其他擴展算法[25-26]。這些群體智能算法通過大量的仿真實驗找到最優值,但是很難保證理論上找到最優值。旅行商問題與本文提出的問題有所不同,本文提出問題中每種架構方案在搜索之前其能力是未知的,服從某種概率分布;確切能力值只有在原型化之后才知道,且在原型化之后架構的能力值是確定不變的。因此,群體智能算法很難直接應用于本文問題。
在面臨重大決策問題時,一般采取的思路是先評估-后決策。而如何評價裝備體系具有一定挑戰性。一種可行的方法是邊實踐邊評估,即基于某種架構搭建體系原型,如果該體系原型具有較高能力值則選擇該體系,反之則繼續根據新的架構搭建體系原型。潘多拉問題[27]主要解決經濟學中的項目方案選擇問題,每種項目方案在實際運用之前并不知道其獲得的價值,通過邊實踐邊評估的方式進行搜索,最終選擇合適的項目。但是潘多拉問題只能選擇一個項目方案,無法直接用于多個方案的選擇問題。Chen[28]也做過類似研究,將潘多拉問題應用于人機協作,但也只能選擇一個方案。順次分配法正好適合求解多方案選擇問題。順次分配法是一種常用協調方法,廣泛應用于資源分配、多機器人路徑規劃等問題。在順序分配機制中,Agent輪流做出決策。在每個回合中,每個Agent選擇策略以基于當前情況獲取最大回報值。
2 裝備體系空間搜索問題
本節給出裝備體系架構定義,提出一種多Agent系統[29]動態規劃問題。
2.1 裝備體系架構的定義
能力用于衡量體系完成使命任務可能性的大小。具體來說,每種裝備系統具有一定功能,通過協同結構相互連接裝備系統具備完成特定使命的能力。裝備體系架構(以下簡稱“架構”)只考慮了裝備體系的核心要素,因此根據該架構所原型化的裝備體系的能力具有不確定性。架構形式化由架構能力、原型化成本以及架構超網絡三部分組成,記為〈W,P,GA〉,其中GA表示架構超網絡。下面分別給出架構能力、原型化成本以及拓撲模型三者定義。
(1)架構能力
架構能力是指裝備體系完成特定使命的能力,記為W。其中裝備體系由裝備體系架構原型化而成。在原型化之前,架構能力不確定性用概率分布表示,記為W。這是因為架構能力可能受一些不確定因素的影響,對于這種不確定因素一般用概率來表示。確切能力是在體系建成之后才能得到,而原型化的過程是需要花費成本的。對于體系架構能力概率分布的選擇和參數賦值,可以采取定性與定量相結合的方法,如層次分析法,在本文中認為已有相關數據。
(2)原型化成本
原型化成本是指根據架構方案建設體系時所花費的成本,記為P。本文假設每個架構的原型化成本是已知的和固定的。
(3)拓撲模型
架構方案可抽象為拓撲模型,是由任務網絡、裝備網絡和協同網絡3種不同類型的子網絡及其相互關系構成。
任務網絡是由任務節點組成的網絡,記為GT=(VT,ET),其中VT表示任務節點,ET表示任務節點之間的關系。任務節點是指裝備系統能夠執行的活動過程,記為T。此處任務是通用概念,例如飛行器的空中遮斷、近距離空中支援、抵近偵察、電子對抗、空運等。根據決策層級不同,任務粒度大小也會不同。對于同一層任務,可以分為并列關系、順序關系、無關聯關系等;對于不同層任務,應自頂向下分解任務,上層任務由下層任務組成,逐層分解直至不用分解為止。一般而言,層與層之間的關系可以包括一對一、一對多、多對一關系、多對多關系等。
裝備網絡是由裝備節點組成的網絡,記為GQ=(VQ,EQ),其中VQ表示裝備功能節點,EQ表示裝備功能節點之間的關系。裝備節點是指具有一定功能,且能夠獨立完成特定任務的裝備系統,記為Q,換句話說裝備網絡也可以認為是功能網絡。根據觀察-調整-決策-行動[30]流程,裝備可以分為偵察裝備、信息處理裝備、指控裝備、打擊裝備、評估裝備、保障裝備等類型。這些類型的節點通過功能依賴關系相互關聯,如偵察無人機具有偵察功能,將收集的目標信息傳遞給指揮部;指揮部具有決策功能,但需要無人機提供的偵察數據;因此兩類節點具備關聯關系。
協同網絡是由協同節點組成的網絡,記為GC=(VC,EC),其中VC表示協同節點,EC表示協同節點之間的關系,例如信息協同、決策協同、行動協同等。協同節點是指用于處理信息、組織管理、決策計劃、控制反饋等活動的邏輯節點,能夠處理上下級之間的指令關系以及同級之間的協作關系,記為C。設計協同網絡的目的是使得所有裝備系統相互聯系以達到預期使命。
任務網絡中任務節點與裝備網絡中的裝備節點映射關系可以抽象為二分圖GTQ=(VT,VQ,ETQ),其中ETQ表示任務節點VT與裝備節點VQ之間的關聯關系。裝備網絡中裝備節點與協同網絡中的協同節點映射關系可以抽象為二分圖GQ C=(VQ,VC,EQ C),其中EQ C表示裝備節點VQ與協同節點VC之間的關聯關系。
架構是由3類節點和5類關系組成的網絡,架構超網絡模型如圖1所示。構建方法如下:第一,將裝備體系使命任務分解為可以由裝備執行的任務網絡;第二,給出能夠完成任務的裝備及其對應關系,并根據任務網絡構建裝備網絡;第三,每個裝備節點都是一個協同節點,在此基礎上建立協同網絡。一般而言,如果超網絡中具有更多的節點或者更復雜的關系,那么架構的原型化成本將會更大,架構能力可能也會更大。架構能力與超網絡之間的映射關系是一個復雜課題,是面向特定領域和不同情況的。因此,本文直接給出每種架構的能力分布,不研究架構能力與超網絡之間的具體映射關系。

圖1 架構超網絡模型示意圖
2.2 架構方案空間搜索問題
對于裝備體系架構選擇問題,最終還是需要決策者做決策。本文旨在提出無人干預情況下的一種自動規劃算法,最終提供若干架構方案以供決策者參考。假設最終需要推薦N個架構,此時可以認為有N個決策者進行決策,每個決策者從各自方案空間中選擇一個架構。將決策者抽象為Agent,那么架構方案空間搜索問題可以抽象為多Agent系統動態規劃問題。不失一般性,以Agentm∈M為例進行說明。

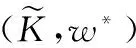

(1)

(2)
參照文獻[28],Agent根據式(2)確定如何選擇行動,其中:

(3)
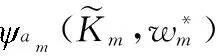
3 動態規劃算法
本節首先提出了一種基于順次分配機制的方案空間搜索(sequential allocation mechanism based scheme space exploration,SAMSSE)算法,然后對SAMSSE算法進行理論分析。
3.1 SAMSSE算法

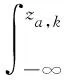
(4)
指標za,k相當于預期回報的評判值,如果該指標越大,則探索該架構所得的回報值越大,反之則越小。
根據式(4),可以推導出:
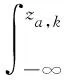

(5)


(6)
不失一般性,本文以Agentm為例進行說明。單個Agent搜索算法可以分為3個階段:指標排序、指標判斷和架構選擇。指標排序是指根據等式(6)計算所有決策指標;指標判斷是指如果Agentm要搜索未知體系架構,則選擇具有最大指標的體系架構和行動;體系架構選擇的準則是,當所收集的最大采樣能力值大于所有未知體系架構的最大指標時,Agentm停止搜索并選擇具有最高采樣回報值的體系架構。SAMSSE算法分為IndicatorSorting和PolicyComputing兩個程序。每次執行SAMSSE算法得到的是一次采樣值,因而需要多次運行以求取期望值。
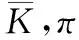

程序1 IndicatorSorting(K)開始 K,π←? c←0 K←KForm∈M,km∈ Km,amk∈Amkdo za,k←Solving(ca,k=∫∞za,k(wk-za,k)dFk(wk)) EndFor Form∈Mdo πm←Sorting(za,k|k∈Km,a∈Amk) π∈π∪πm EndFor Returnπ結束


程序2 PolicyComputing(K,π)開始 Form∈Mdo w*m←0 Fori=1to|Km|do km←arcmaxkm∈ Km(πm) akm←arcmaxak∈Akm(πm(km)) Ifw*m 本文的主要創新之處在于結合潘多拉規則與順次分配方法,解決多無人裝備體系架構方案選擇問題。 SAMSSE計算時間復雜度與排序算法一致。從IndicatorSorting可以獲知,SAMSSE算法的計算時間復雜度取決于排序算法的計算時間復雜度,例如堆排序的時間復雜度為O(nlgn)、冒泡排序的平均時間復雜度為O(n2)。每個Agent都根據體系架構的決策指標進行排序,在程序運行過程中該順序始終保持不變。因此在整個程序運行過程中,該算法時間復雜度等于排序算法的時間復雜度。 本節設定若干場景,通過仿真實驗分析SAMSSE算法的性能。 假設要建立一種由無人機集群和無人車集群組成的新質力量體系,完成諸如邊境巡邏、持續偵察和電磁干擾等任務。對于這樣的新使命新力量,如何建立無人體系是首要問題。本文提供的模型框架是一種可選擇的方法:第一,將使命分解為任務網絡;第二,這些任務可由具有某些功能的無人機或無人車完成,由此建立無人系統與任務之間的關系,以及無人系統之間的功能依賴關系;第三,每個無人平臺都是一個協同節點,根據需求建立協同網絡。 本實驗定義了一些算法性能評估指標如下。 (1)回報值:采樣能力值和累計原型化成本之間的差值。回報值不僅體現了裝備體系架構的能力值,同時也體現了架構篩選是需要花費代價的。 (2)運行時間:運行一輪仿真實驗耗費的時間。 本文設計了3個場景來評估算法的可擴展性。架構方案空間大小|K|分別為50、500、5 000。每種架構的原型化有3種,其原型化成本分別遵守不同的均勻分布c1~U(10,20),c2~U(5,30),c3~U(15,25)。每個架構k的能力值服從概率分布wk~U(p1,p2),其中p1~U(500,1 000),p2~U(1 000,2 000)。令選擇的架構方案數量(number of selection,NoS)為1到10,排序方法為冒泡排序法。 場景 1在|K|=50的方案空間中搜索。 場景 2在|K|=500的方案空間中搜索。 場景 3在|K|=5 000的方案空間中搜索。 (1)場景1 圖2(a)展示了場景1中SAMSSE、EVP和RS的平均回報值,表明隨著NoS的增加,平均回報值增加,且SAMSSE的平均回報值略高于其他算法。圖2(b)展示了場景1中SAMSSE、EVP和RS的平均運行時間,表明SAMSSE平均運行時間略高于其他兩種算法。 圖2 場景1仿真運行結果 (2)場景2 圖3(a)展示了場景2中SAMSSE、EVP和RS的平均回報值,表明SAMSSE的平均回報值略高于其他算法。圖3(b)展示了3種算法的平均運行時間,表明SAMSSE平均運行時間略高于其他兩種算法。 圖3 場景2仿真運行結果 (3)場景3 圖4(a)展示了場景3中SAMSSE、EVP和RS的平均回報值,其中部分RS結果未顯示,這是因為其結果為負數。與前面的實驗結果一樣,SAMSSE的平均回報值遠高于其他算法。圖4(b)展示了場景3中SAMSSE、EVP和RS的平均運行時間,實驗結果表明SAMSSE平均運行時間略高于其他兩種算法。 圖4 場景3仿真運行結果 (4)縱向對比 對場景1~場景3中SAMSSE算法的平均回報值和平均運行時間進行比較,平均回報值如圖5(a)所示。實驗結果表明,隨著NoS的增加,平均回報值隨之而增加。平均運行時間如圖5(b)所示,實驗結果表明隨著NoS的增加,平均運行時間呈多項式增長。 圖5 不同場景下SAMSSE仿真實驗結果 總的來說,這些實驗結果表明SAMSSE的性能優于RS和EVP。原因在于SAMSSE通過基于最優決策指標的方法順次選擇架構,從而能夠找到最優的搜索路線。 根據以上仿真結果,可以發現SAMSSE算法有一些有趣的現象。首先,SAMSSE算法是一種順序分配方法,因而隨著變量NoS的增加,回報值也會增加。其次,運行時間增加幅度可能會隨著NoS的增加而降低。一方面,每輪都會重新篩選并選擇一種新架構,因而總運行時間將逐漸增加;另一方面,已經探索了但未選擇的架構可以用作后續采樣的先驗條件,故后續Agent可能在探索更少的架構情況下便停止搜索,因此運行時間的增量可能會減少。第三,實驗結果表明SAMSSE的性能優于RA和EVP。原因是SAMSSE通過基于決策指標的方法貪婪地選擇架構。該指標是根據特定的問題特征計算的,并被證明是在特定條件下得到最優搜索策略,從而可以找到較好的搜索路徑并選擇最佳的架構。 本文提出了一種面向任務的裝備體系架構設計方法,為無人體系等新質力量裝備體系架構的構建及選擇提供思路。本文提出了一種基于超網絡的裝備體系架構模型,并提出一種方案空間搜索算法。該問題的目標是在給定架構方案空間中選擇若干最優架構。具體而言,架構空間搜索過程被建模為一種多Agent動態規劃問題。假設在搜索之前獲知每種架構能力的概率分布,但在架構被原型化之前其具體能力是未知的。為了解決這一問題,提出了一種基于決策指標的順次分配算法。通過理論分析和仿真實驗,證明和驗證了該算法的計算時間復雜度是多項式的且回報值可能是最優的,回報值遠高于其他基準算法而運行時間與其他算法相近。3.2 性能分析

4 仿真實驗
4.1 實驗設置
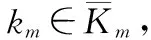
4.2 實驗結果




4.3 實驗分析
5 結 論

