輪對系統(tǒng)的Hopf 分岔研究1)

武世江 張繼業(yè) ,2) 隋 皓 殷中慧 胥 奇

* (西南交通大學牽引動力國家重點實驗室,成都 610031)

? (西南交通大學力學與工程學院,成都 610031)

引言

近年來隨著高速列車運行速度的提高,車輛系統(tǒng)的蛇行失穩(wěn)問題越發(fā)突出,蛇形運動作為車輛系統(tǒng)的固有屬性,嚴重影響著車輛系統(tǒng)的運行平穩(wěn)性、乘坐舒適性和安全性[1],對車輛系統(tǒng)進行非線性動力學理論方面的研究,不僅可以從車輛動力學角度更加全面地了解蛇形運動,而且對車輛系統(tǒng)的設計與參數(shù)優(yōu)化也具有非常重要的意義.

在國外研究中,True[2]用延續(xù)算法求解了非線性車輛系統(tǒng)中的分岔問題.Wagner[3]將非線性輪軌力分段函數(shù)擬合為關于橫移量的三次方與五次方的疊加函數(shù),并用該非線性輪軌函數(shù)求解了輪對系統(tǒng)的分岔圖,極大地方便了理論研究非線性輪軌接觸對輪對蛇形運動的影響.Zboinski 和Dusza[4-6]研究了車輛系統(tǒng)中懸掛參數(shù)、曲線半徑、踏面和車輪名義滾動圓半徑在曲線軌道上的穩(wěn)定性.Kim 等[7]建立了31 個自由度的車輛系統(tǒng)動力學模型,通過分岔圖研究發(fā)現(xiàn)輪對系統(tǒng)的線性臨界速度對應亞臨界Hopf 分岔,而非線性臨界速度對應的是一個鞍結(jié)點.Park 等[8]利用分岔理論研究了懸掛參數(shù)與輪軌接觸關系對車輛系統(tǒng)蛇形運動的影響,發(fā)現(xiàn)輪軌接觸關系比懸掛參數(shù)更加影響車輛系統(tǒng)的蛇形運動.

在國內(nèi)研究中,張衛(wèi)華等[9-10]通過研究Poincaré 映射面上不動點的穩(wěn)定性,得到了軌道車輛系統(tǒng)的周期解,并將其結(jié)果與滾動振動試驗臺所得結(jié)果進行對比分析,解釋了相關結(jié)果出現(xiàn)差異的可能原因.曾京[11]針對17 個自由度的經(jīng)典客車模型,應用QR 算法和黃金分割法計算了該客車系統(tǒng)蛇形失穩(wěn)的臨界速度,并用打靶法對其領域的極限環(huán)進行了求解.張繼業(yè)等[12-13]利用Hurwitz 行列式得到了平衡點失穩(wěn)的Hopf 分岔代數(shù)判據(jù),極大地方便了車輛系統(tǒng)中尋找Hopf 分岔點的過程.黃世凱[14]在研究輪對系統(tǒng)陀螺效應的時候,定義了輪對系統(tǒng)的陀螺力貢獻率,但其并沒有從Hopf 分岔的角度研究陀螺效應.董浩等[15-16]建立了中國高速動車組CRH2和CRH3 的轉(zhuǎn)向架和半車車輛系統(tǒng)動力學模型,采用范式法證明了其在簡單輪軌接觸關系下均存在亞臨界和超臨界Hopf 分岔,但并沒有建立整車動力學模型,所以該結(jié)論不一定適應整車動力學模型.高學軍等[17-20]對車輛系統(tǒng)提出了“合成分岔圖”,研究發(fā)現(xiàn)車輛系統(tǒng)在擬周期運動后出現(xiàn)混沌現(xiàn)象.張波等[21-22]對輪對系統(tǒng)的陀螺效應進行了分析,對比了考慮陀螺效應與不考慮陀螺效應的分岔圖,研究發(fā)現(xiàn)陀螺力不做功,具有增穩(wěn)效果.Zeng 等[23]在研究輪對系統(tǒng)的陀螺效應時發(fā)現(xiàn),輪對系統(tǒng)的陀螺效應關于縱向的分量會降低系統(tǒng)的穩(wěn)定性,而關于垂向的分量有助于提高系統(tǒng)的穩(wěn)定性,兩者的綜合作用可以提高車輛系統(tǒng)的臨界速度并抑制極限環(huán)的幅值.張婷婷等[24-25]研究了單輪對系統(tǒng)的Hopf 分岔類型及其遷移機理,但該模型過于簡單,沒有考慮陀螺效應和阻尼約束.Ge 等[26]用實測踏面數(shù)據(jù)修正了輪軌非線性關系,使用MATCONT 求解了修正后的輪對系統(tǒng)的周期解,但對修正后的輪對系統(tǒng)出現(xiàn)的部分周期解缺少相關理論解釋.

目前關于輪對系統(tǒng)非線性動力學的文獻中,缺少同時考慮陀螺效應和退化Hopf 分岔理論的研究.本文在文獻[3]的基礎上,研究輪對系統(tǒng)中有、無陀螺效應對單參數(shù)下的Hopf 分岔類型以及雙參數(shù)下的退化Hopf 分岔的影響.

1 考慮陀螺效應的輪對模型

1.1 輪對模型建立

輪對系統(tǒng)作為機車車輛里面最簡單的系統(tǒng),研究輪對系統(tǒng)可以從原理上簡單的解釋蛇形運動.如圖1 所示,假設輪對系統(tǒng)在直線軌道上做微幅振動,輪軌之間采用kalker[27]線性蠕滑模型,建立考慮陀螺效應、剛度約束和非線性輪軌關系的輪對系統(tǒng)動力學模型.

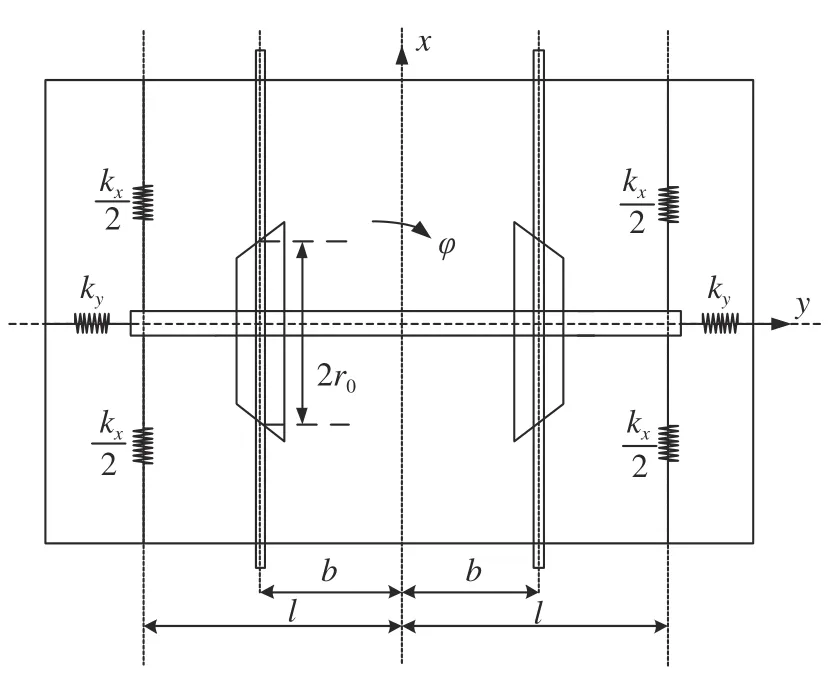
圖1 輪對模型圖Fig.1 Wheelset model diagram

記x=(y,φ)T,主要影響輪對系統(tǒng)蛇形運動的橫移和搖頭運動方程為[3]

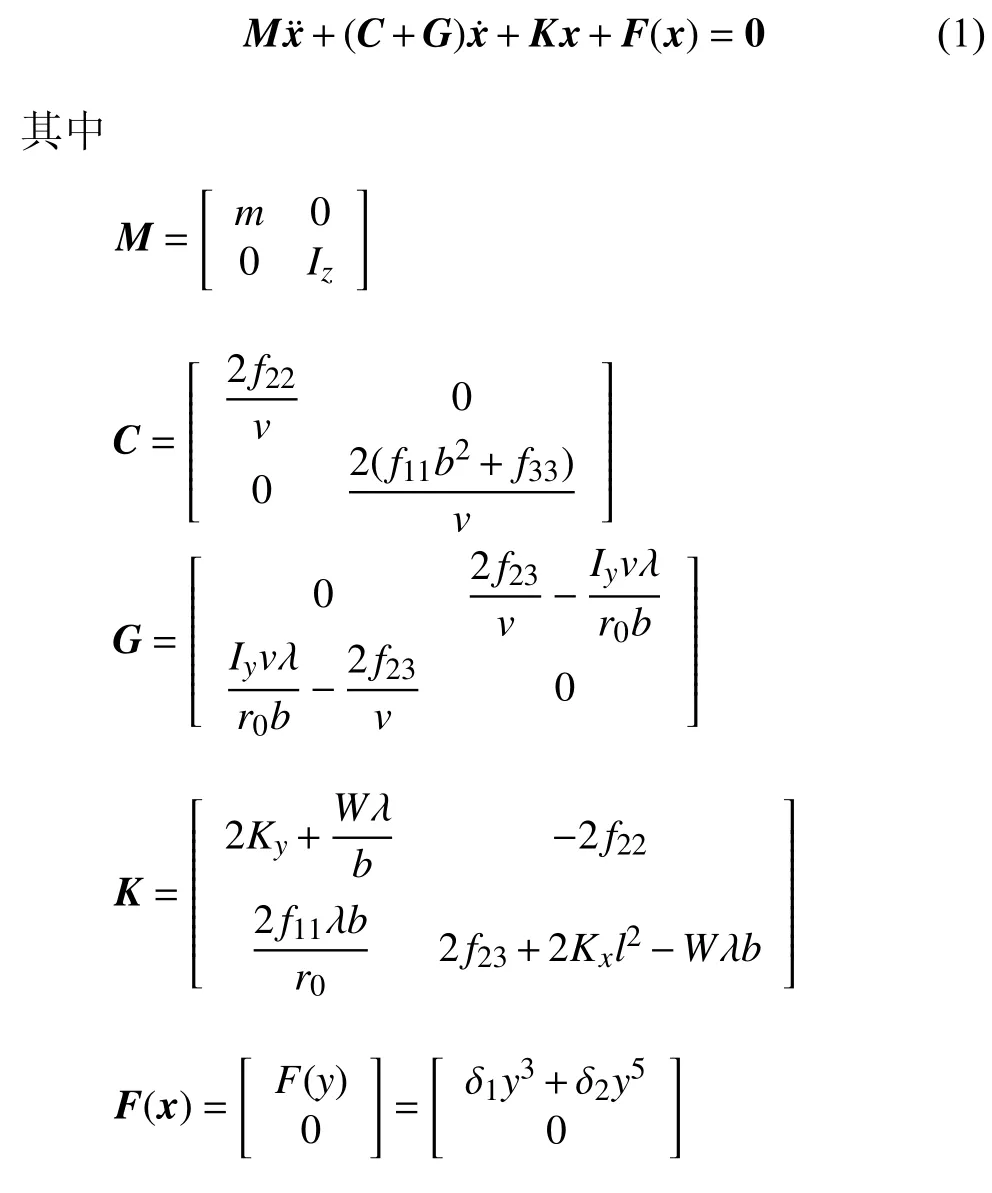
式中m,Iz,Iy和W分別為輪對質(zhì)量、垂向轉(zhuǎn)動慣量、橫向轉(zhuǎn)動慣量和軸重;r0,b,l和 λ 分別為名義滾動圓半徑、兩滾動圓跨距之半、左右懸掛距離之半和踏面等效錐度;kx和ky分別為縱向和橫向剛度;f11,f22,f23和f33分別為縱向蠕 滑系數(shù)、橫向蠕 滑系數(shù)、橫向自旋蠕滑系數(shù)和自旋蠕滑系數(shù);δ1和 δ2為非線性輪軌力系數(shù);v為輪對運行速度,以上各參數(shù)取值見附錄A 中表A1.

方程(1)中的矩陣G為陀螺矩陣[21],可以看出影響輪對系統(tǒng)陀螺效應的主要參數(shù)是橫向自旋蠕滑系數(shù)和橫向轉(zhuǎn)動慣量.本文將動力學方程中不考慮橫向自旋蠕滑系數(shù)和橫向轉(zhuǎn)動慣量的輪對系統(tǒng)稱為不考慮陀螺效應的輪對系統(tǒng),動力學方程中考慮橫向自旋蠕滑系數(shù)和橫向轉(zhuǎn)動慣量的輪對系統(tǒng)稱為考慮陀 螺效應的輪對系統(tǒng).

1.2 輪對系統(tǒng)在Hopf 分岔點處的線性臨界速度表達式推導

式中p1,p2,p3,f1,f2,g,s和c的具體表達式見附錄B 中式(B1)～ 式(B8).

方程(2)的線性部分對應的特征方程如下

根據(jù)Hopf 分岔代數(shù)判據(jù)[12]可知,方程(4)的4 個特征值中存在一對純虛根且其余兩個根的實部均為負數(shù)的條件為

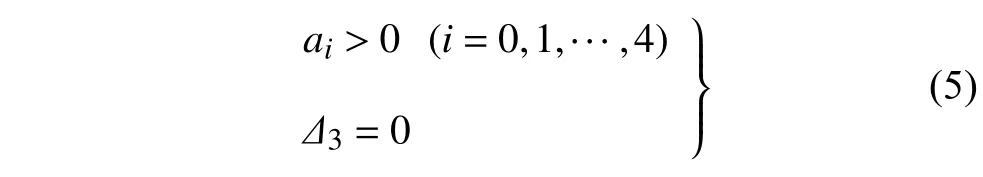
其中 Δ3為Hurwitz 行列式.

由方程(5) 可知,當輪對系統(tǒng)的參數(shù)滿足ai>0 (i=0,1,···,4) 時,令 Δ3=0可得關于輪對系統(tǒng)運行速度v的一元六次方程如下

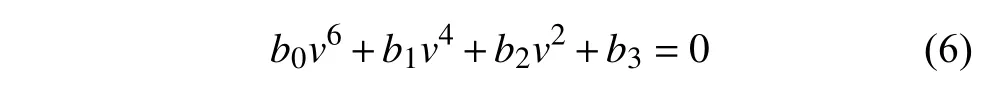
其中b0,b1,b2和b3的具體表達式參見附錄B 中式(B9)～ 式(B12).

令v2=d,由方程(6)可得關于x的一元三次方程如下

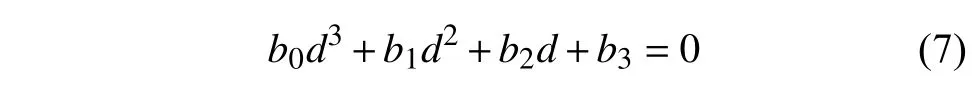
在Hopf 分岔點處,輪對系統(tǒng)有且僅有一個線性臨界速度(正實數(shù)),故方程(7)中的一元三次方程的根中必須有且僅有一個正實根,根據(jù)文獻[28]中對一元三次方程根的討論,令可得考慮陀螺效應的輪對系統(tǒng),在Hopf 分岔點處的線性臨界速度表達式為

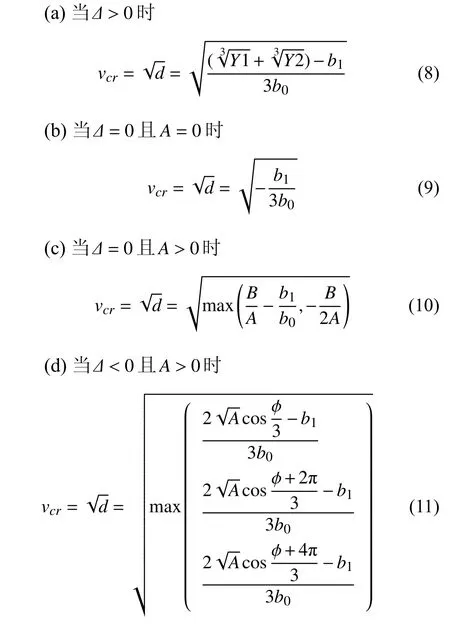
其中

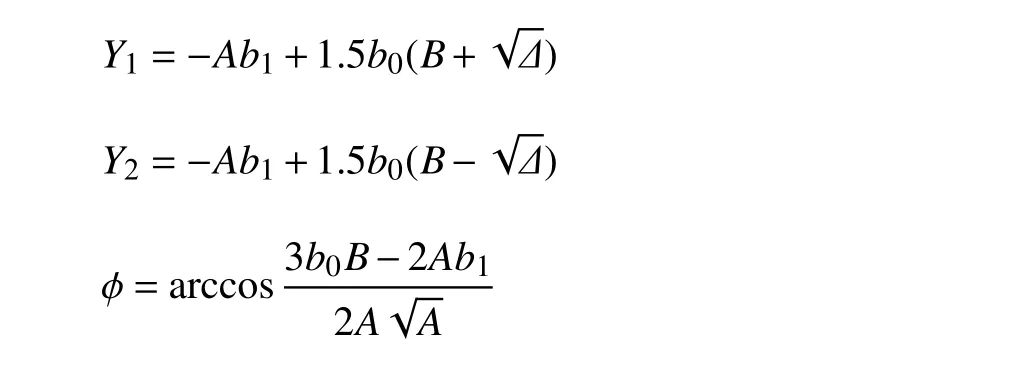
不考慮陀螺效應的輪對系統(tǒng),即橫向自旋蠕滑系數(shù)和橫向轉(zhuǎn)動慣量均為零時,方程(7)中的系數(shù)b0和b1變?yōu)榱?b2和b3也會分別簡 化為b22和b33,b22和b33的表達式見附錄B 中式(B13)和式(B14),方程(7)簡化為一元一次方程

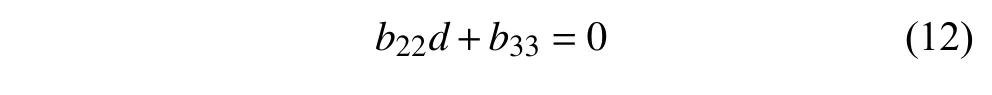
求得不考慮陀螺效應的輪對系統(tǒng)在Hopf 分岔點處的線性臨界速度表達式為

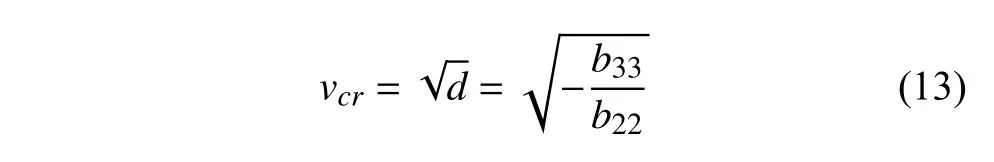
其與文獻[24]中是一樣的.

取縱向剛度為4 MN/m,其他參數(shù)取值見附錄A 中表A1,將參數(shù)值代入本文推導的考慮陀螺效應的輪對系統(tǒng)線性臨界速度解析表達式(8)～ 式(11)與不考慮陀螺效應的輪對系統(tǒng)線性臨界速度解析表達式(13),求得考慮陀螺效應的輪對系統(tǒng)在Hopf 分岔點處的線性臨界速度值為140.5364 m/s,不考慮陀螺效應的輪對系統(tǒng)在Hopf 分岔點處的線性臨界速度值為135.4532 m/s.

同理取縱向剛度kx為4 MN/m,其他參數(shù)取值見附錄A 中表A1,對方程(2)的線性部分使用根軌跡法[11]求解Hopf 分岔點處輪對系統(tǒng)的線性臨界速度,即設初速度為v0,步長為 Δv和特征值控制精為ep.令v=v0,計算速度v對應的方程(2) 中J(v)矩陣的特征值.然后對每一個速度v對應下的所有特征值的實部取絕對值,找出每一個速度v對應的特征值實部絕對值的最大值 |Rmax|,若 |Rmax|≤ep,則此時的速度就是輪對系統(tǒng)在Hopf 分岔點處的線性臨界速度.若|Rmax|>ep,此 時 當Rmax<0 時,則 設v=v0+Δv,當Rmax>0 時,則v=v0?Δv,重復以上計算過程,直到得到滿足控制精度ep的輪對系統(tǒng)Hopf 分岔線性速度值為止.最后求得考慮陀螺效應的輪對系統(tǒng)在Hopf 分岔點處的線性臨界速度值為140.5364 m/s,不考慮陀螺效應的輪對在Hopf 分岔點處的線性臨界速度值為135.4532 m/s.

該結(jié)果與本文推導的考慮陀螺效應的輪對系統(tǒng)線性臨界速度解析表達式(8)～ 式(11)與不考慮陀螺效應的輪對系統(tǒng)線性臨界速度解析表達式(13)的結(jié)果是一樣的.

1.3 輪對系統(tǒng)的陀螺效應參數(shù)分析

由方程(1)中的陀螺矩陣G可知,影響輪對系統(tǒng)陀螺效應的主要參數(shù)為橫向自旋蠕滑系數(shù)和橫向轉(zhuǎn)動慣量,假設橫向自旋蠕滑系數(shù)和橫向轉(zhuǎn)動慣量的數(shù)值變化不引起輪對系統(tǒng)其他參數(shù)的變化.

取縱向剛度值為4 MN/m,橫向自旋蠕滑系數(shù)分別取0.01 MN,0.13 MN 與0.2 MN,橫向轉(zhuǎn)動慣量的值從50 k g·m2取到150 k g·m2,其他參數(shù)取附錄A 中表A1,將其代入式(8)～ 式(11)中,得到考慮陀螺效應的輪對系統(tǒng)中,線性臨界速度與橫向轉(zhuǎn)動慣量的關系如圖2 所示.

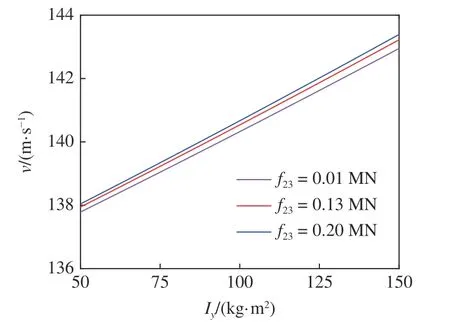
圖2 輪對系統(tǒng)線性臨界速度與橫向轉(zhuǎn)動慣量的關系Fig.2 The relationship between the linear critical speed of the wheelset system and the lateral moment of inertia

取縱向剛度為4 MN/m,橫向轉(zhuǎn)動慣量分別取80 k g·m2,100 k g·m2與120 k g·m2,橫向自旋蠕滑系數(shù)的值從0.001 MN 取到0.25 MN,其他參數(shù)取附錄A 中表A1,將其代入式(8)～ 式(11)中,得到考慮陀螺效應的輪對系統(tǒng)中,線性臨界速度與橫向自旋蠕滑系數(shù)的關系如圖3 所示.

圖2 與圖3 中Iy為輪對系統(tǒng)的橫向轉(zhuǎn)動慣量,v為輪對系統(tǒng)的運行速度,f23為輪對系統(tǒng)的橫向自旋蠕滑系數(shù).由圖2 可知,在同一橫向自旋蠕滑系數(shù)下,輪對系統(tǒng)的線性臨界速度隨著橫向轉(zhuǎn)動慣量的增大而增大,該變化趨勢比較明顯.在同一橫向轉(zhuǎn)動慣量下,橫向自旋蠕滑系數(shù)分別為0.01 MN,0.13 MN與0.2 MN 對應的輪對系統(tǒng)的線性臨界速度依次增大,該變化趨勢不太明顯.由圖3 可知,在同一橫向轉(zhuǎn)動慣量下,輪對系統(tǒng)的線性臨界速度隨著橫向自旋蠕滑系數(shù)的增大而增大,該變化趨勢不太明顯.在同一橫向自旋蠕滑系數(shù)下,橫向轉(zhuǎn)動慣量分別為80 k g·m2,100 k g·m2與120 k g·m2對應的輪對系統(tǒng)的線性臨界速度依次增大,該變化趨勢比較明顯.

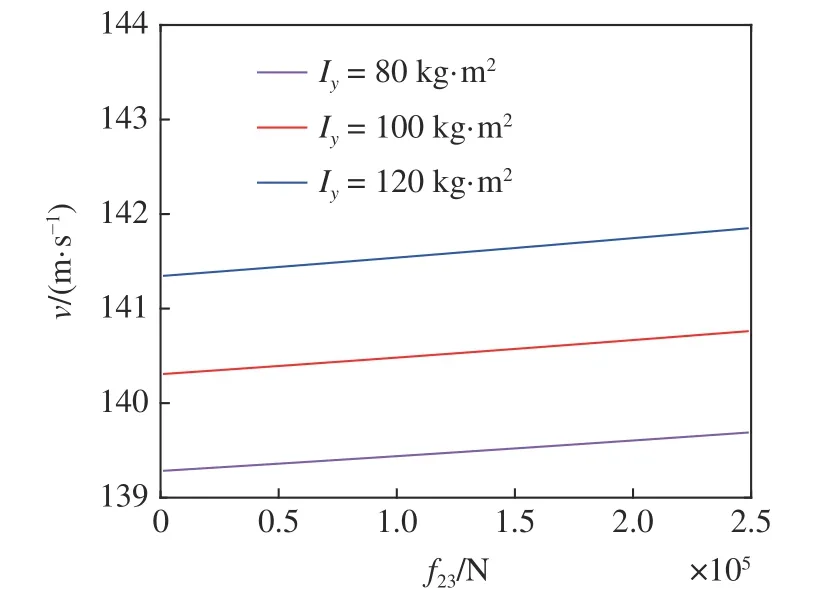
圖3 輪對系統(tǒng)的線性臨界速度與橫向自旋蠕滑系數(shù)關系Fig.3 The relationship between the linear critical speed of the wheelset system and the lateral spin-slip coefficient

對比圖2 與圖3 可知,橫向轉(zhuǎn)動慣量在輪對系統(tǒng)陀螺效應中起主導作用,橫向自旋蠕滑系數(shù)起次要作用.

2 輪對系統(tǒng)第一、第二Lyapunov 系數(shù)的求解

為更好地研究輪對系統(tǒng)在Hopf 分岔點處的運動形式,采用分岔理論中的投影法[29-30]求解輪對系統(tǒng)的第一、第二Lyapunov 系數(shù),從而方便研究輪對系統(tǒng)在單參數(shù)下的Hopf 分岔類型與雙參數(shù)下的退化Hopf 分岔類型.

2.1 輪對系統(tǒng)第一Lyapunov 系數(shù)求解

在輪對系統(tǒng)的Hopf 分岔點處,即v=vcr時,方程(2) 中的矩陣J(v)的特征值中存在一對純虛根±ω0i 與兩個具有負實部的根,設矩陣J(v)的特征值為純虛根時對應的特征向量為q=[x1,x2,x3,x4]T,滿足J(v)q=iω0q,其中

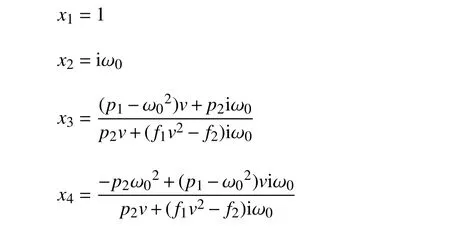
在輪對系統(tǒng)的Hopf 分岔點處,即v=vcr時,方程(2)中的矩陣J(v) 的轉(zhuǎn)置矩陣為JT(v),該轉(zhuǎn)置矩陣的特征值中存在一對純虛根 ± iω0和兩個具有負實部的根,設矩陣JT(v)的特征值為純虛根時對應的特征向量為p=[x11,x22,x33,x44]T,滿足JT(v)p=?iω0p,其中

從方程(1)中可知非線性輪軌力為關于橫移量的三次方和五次方的疊加,根據(jù)投影法[29-30]求解可得

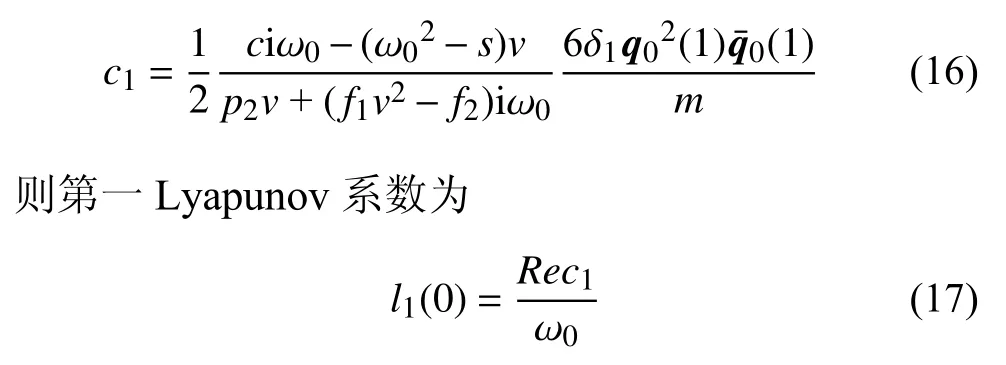
當系統(tǒng)在平衡點發(fā)生Hopf 分岔時,若第一Lyapunov 系數(shù)大于零,系統(tǒng)發(fā)生亞臨界Hopf 分岔.若第一Lyapunov 系數(shù)小于零,系統(tǒng)發(fā)生超臨界Hopf 分岔.若第一Lyapunov 系數(shù)等于零,系統(tǒng)發(fā)生退化的Hopf 分岔.故可通過計算輪對系統(tǒng)的第一Lyapunov 系數(shù)判斷系統(tǒng)發(fā)生的Hopf 分岔類型.

2.2 輪對系統(tǒng)第二Lyapunov 系數(shù)求解

為研究第一Lyapunov 系數(shù)等于零時輪對系統(tǒng)在退化Hopf 分岔點附近的Bautin 分岔形式,根據(jù)投影法[29-30]求解輪對系統(tǒng)的第二Lyapunov 系數(shù),其中輪對系統(tǒng)對應的投影法中各系數(shù)分別如下

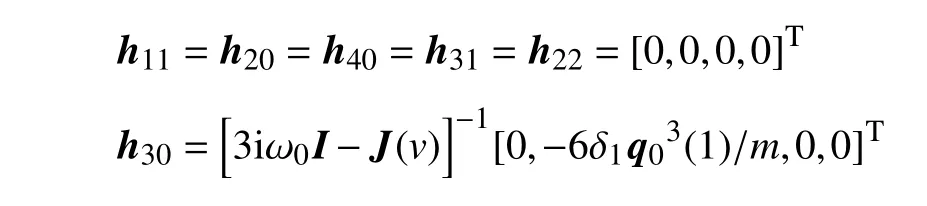
3 輪對系統(tǒng)的分岔圖

3.1 采用打靶法求解輪對系統(tǒng)分岔圖

采用打靶法[11]求解輪對系統(tǒng)的分岔圖,其原理為假設極限環(huán)周期為T,滿足Y(t+T)=Y(t),令t=Tz,則方程(2)可以被表示為

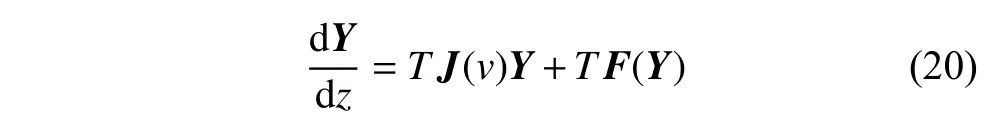
方程(20)滿足邊界條件Y(1)=Y(0),對方程(20)在區(qū)間[0,1]內(nèi)積分可以得到Y(jié)(1)=G(Y,T,v),使得其滿足

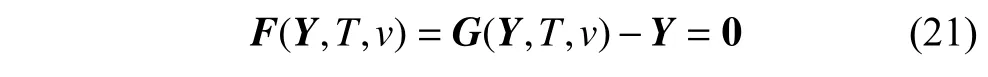
通過使用得到的輪對系統(tǒng)在Hopf 分岔點處的線性臨界速度表達式(8)～ 式(11)與式(13),參數(shù)值代入附錄A 中表A1,計算輪對系統(tǒng)Hopf 分岔點處的線性臨界速度vcr.

取初值分別為T0=2π/ω0,v0=vcr,y=y0,=0,φ=0 和=0,其中,y0為輪對橫移量初始微小擾動,使用Newton?Raphson 迭代法[31]求解方程(21),每次使用Newton?Raphson 迭代法求解方程(21)的過程中,都要用變步長歐拉法[31]在區(qū)間[0,1]內(nèi)積分求解方程(21),并判斷F(Y,T,v)的范數(shù)是否滿足控制精度,若滿足則得到輪對系統(tǒng)的極限環(huán)解(輪對橫移量周期解),然后選取下一極限環(huán)的初值為y=y0+h(h為步長)與=0,其他值取前一極限環(huán)的值,重復循環(huán)計算最終可以得到輪對系統(tǒng)的分岔圖.

令D=?G/?Y,當矩陣D的特征值最大模小于1 時,極限環(huán)穩(wěn)定,否則不穩(wěn)定.

為對比考慮陀螺效應與不考慮陀螺效應對輪對系統(tǒng)分岔圖的影響,取輪對系統(tǒng)的縱向剛度分別為4.0 MN/m,5.0 MN/m,5.5 MN/m,6.0 MN/m,6.5 MN/m 與7.0 MN/m,其他參數(shù)值取附錄A 中表A1,采用打靶法[11]求解出不同縱向剛度值下不考慮陀螺效應與考慮陀螺效應的輪對系統(tǒng)分岔圖如下圖4與圖5 所示.

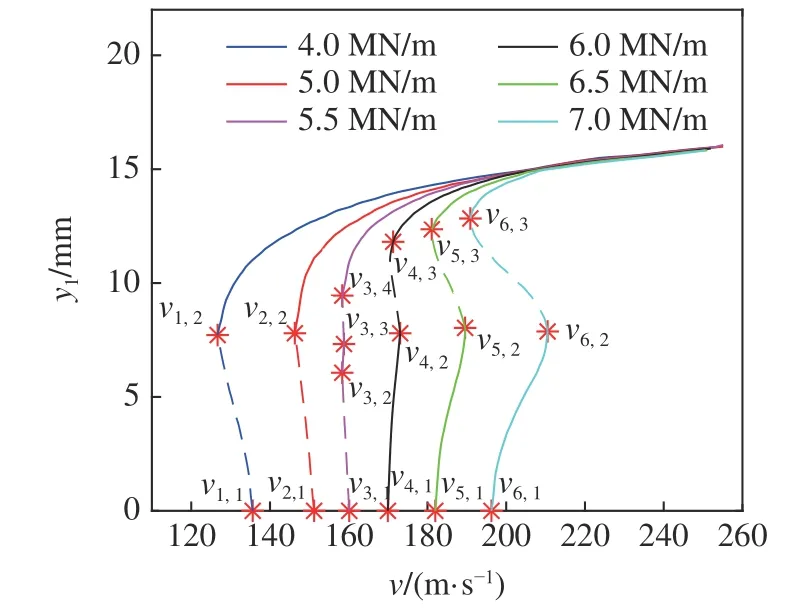
圖4 不同縱向剛度下不考慮陀螺效應的輪對系統(tǒng)分岔圖Fig.4 The bifurcation diagram of wheelset system without considering the gyroscopic action under different longitudinal stiffness

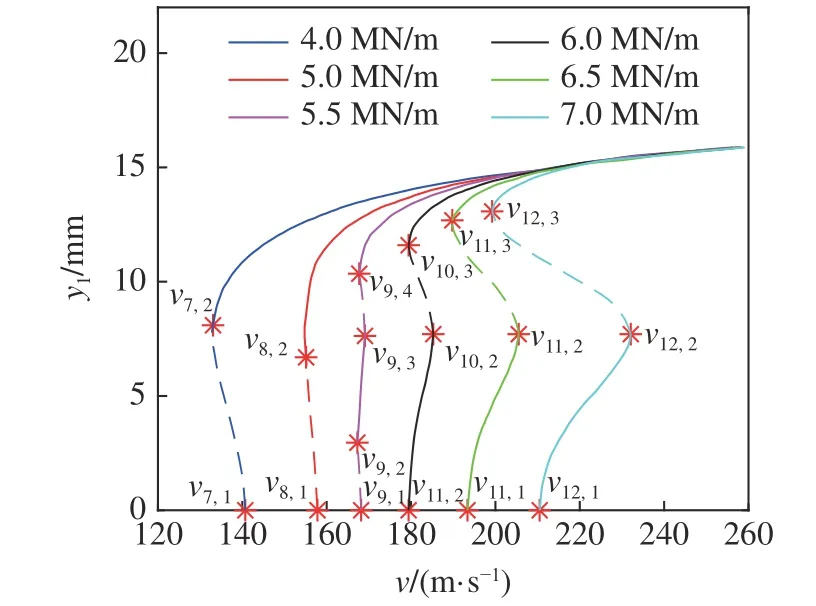
圖5 不同縱向剛度下考慮陀螺效應的輪對系統(tǒng)分岔圖Fig.5 The bifurcation diagram of wheelset system considering the gyroscopic action under different longitudinal stiffness

圖中y1表示輪對系統(tǒng)的橫移量,v表示輪對系統(tǒng)的運行速度,實線表示穩(wěn)定的極限環(huán),虛線表示不穩(wěn)定極限環(huán).vi,j(i=1,2,···,12;j=1)為輪對系統(tǒng)的線性臨界速度,其余的vi,j為輪對系統(tǒng)的非線性臨界速度,各值見附錄A 中表A2 與表A3.

由方程(17)可得,圖4 中不考慮陀螺效應的輪對系統(tǒng),縱向剛度依次取4.0 MN/m,5.0 MN/m,5.5 MN/m,6.0 MN/m,6.5 MN/m 與7.0 MN/m 時,分別對應的第一Lyapunov 系數(shù)依次為0.051 5,0.0238,0.0108,?0.0024,?0.0168 與?0.033 6.圖5 中考慮陀螺效應的輪對系統(tǒng),縱向剛度依次取4.0 MN/m,5.0 MN/m,5.5 MN/m,6.0 MN/m,6.5 MN/m 與7.0 MN/m 時,分別對應的第一Lyapunov系 數(shù) 依 次 為0.045 2,0.017 2,0.003 7,?0.010 3,?0.0258 與?0.044 2.可知當縱向剛度為4.0 MN/m,5.0 MN/m,5.5 MN/m 時,考慮陀螺效應與不考慮陀螺效應的輪對系統(tǒng)第一Lyapunov 系數(shù)均大于零,即輪對系統(tǒng)在Hopf 分岔點處發(fā)生亞臨界Hopf 分岔.當縱向剛度為6.0 MN/m,6.5 MN/m,7.0 MN/m 時,考慮陀螺效應與不考慮陀螺效應的輪對系統(tǒng)第一Lyapunov 系數(shù)均小于零,即輪對系統(tǒng)在Hopf 分岔點處發(fā)生超臨界Hopf 分岔.

圖4 與圖5 對比可知,輪對系統(tǒng)的縱向剛度依次取4.0 MN/m,5.0 MN/m,5.5 MN/m,6.0 MN/m,6.5 MN/m 與7.0 MN/m 時,考慮陀螺效應與不考慮陀螺效應的輪對系統(tǒng)均經(jīng)歷了從亞臨界Hopf 分岔到超臨界Hopf 分岔的變化,在輪對系統(tǒng)中,當縱向剛度值與其他各參數(shù)值均已知時,考慮陀螺效應的線性臨界速度和非線性臨界速度均高于不考慮陀螺效應的線性臨界速度和非線性臨界速度,即在同一縱向剛度值下,陀螺效應既可以提高輪對系統(tǒng)的線性臨界速度,又可以提高輪對系統(tǒng)的非線性臨界速度,陀螺效應對輪對系統(tǒng)具有增穩(wěn)效果.

3.2 輪對系統(tǒng)在退化Hopf 分岔點處的分岔圖

由分岔理論[29-30]可知,若在Hopf 分岔點處系統(tǒng)滿足第一Lyapunov 系數(shù)為零,系統(tǒng)發(fā)生退化Hopf分岔.

針對輪對系統(tǒng),若考慮陀螺效應,輪對橫向轉(zhuǎn)動慣量取100 k g·m2,橫向自旋蠕滑系數(shù)取0.13 MN,其他參數(shù)取值見附錄A 中表A1,根據(jù)第一Lyapunov系數(shù)表達式(17)與Hopf 分岔點處的線性臨界速度表達式(8)～ 式(11),得到考慮陀螺效應的輪對系統(tǒng)在退化Hopf 分岔點處的縱向剛度與輪對線性臨界速度分別為kc1與vc1

針對輪對系統(tǒng),若不考慮陀螺效應,輪對系統(tǒng)的橫向轉(zhuǎn)動慣量取0 k g·m2,橫向自旋蠕滑系數(shù)取0 MN,其他參數(shù)取值見附錄A 中表A1,根據(jù)第一Lyapunov 系數(shù)表達式(17)與Hopf 分岔點處的線性臨界速度表達式(13),得到不考慮陀螺效應的輪對系統(tǒng)在退化Hopf 分岔點處的縱向剛度與輪對線性臨界速度分別為kc2與vc2

采用打靶法[11]分別計算考慮陀螺效應與不考慮陀螺效應的輪對系統(tǒng)在退化Hopf 分岔點處的分岔圖如下圖6 所示.

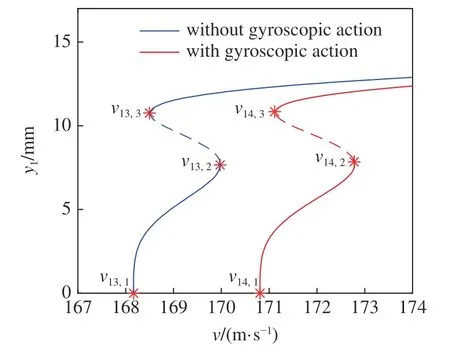
圖6 輪對系統(tǒng)退化Hopf 分岔圖Fig.6 Degenerate Hopf bifurcation diagram of the wheelset system

圖中y1表示輪對系統(tǒng)的橫移量,v表示輪對系統(tǒng)的運行速度,實線表示穩(wěn)定的極限環(huán),虛線表示不穩(wěn)定極限環(huán).v13,1與v14,1為輪對系統(tǒng)的線性臨界速度,且v13,1=vc1,v14,1=vc2,vi,j(i=13,14;j=2,3)為輪對系統(tǒng)的非線性臨界速度,其值參見附錄A 中表A4.

由圖6 可知,考慮陀螺效應與不考慮陀螺效應的輪對系統(tǒng)在各自的退化Hopf 分岔點處,考慮陀螺效應的線性臨界速度與非線性臨界速度值均高于不考慮陀螺效應的輪對系統(tǒng).

4 輪對系統(tǒng)的退化Hopf 分岔形式

4.1 輪對系統(tǒng)在退化Hopf 分岔點處的Bautin 分岔拓撲形式

當?shù)谝籐yapunov 系數(shù)為零時,輪對系統(tǒng)發(fā)生退化Hopf 分岔.

根據(jù)文獻[30]中對于退化Hopf 分岔的討論可知,兩參數(shù)平面系統(tǒng)經(jīng)過一系列時間尺度變換最終可化簡為

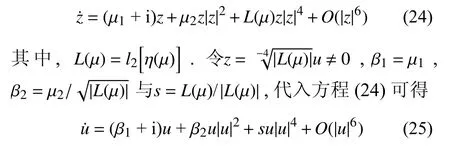
當L(μ)>0,即退化H o p f 分岔點處的第二Lyapunov 系數(shù)大于零時,s=1 .當L(μ)<0,即退化Hopf 分岔點處的第二Lyapunov 系數(shù)小于零時,s=?1.

由式(19)、式(22)與式(23)可得,考慮陀螺效應和不考慮陀螺效應的輪對系統(tǒng)在退化Hopf 分岔點處的第二Lyapunov 系數(shù)分別為?0.01478 與?0.01463,均小于零,結(jié)合方程(25)可知,有、無陀螺效應的輪對系統(tǒng)對應的Bautin 分岔[30]的形式均為

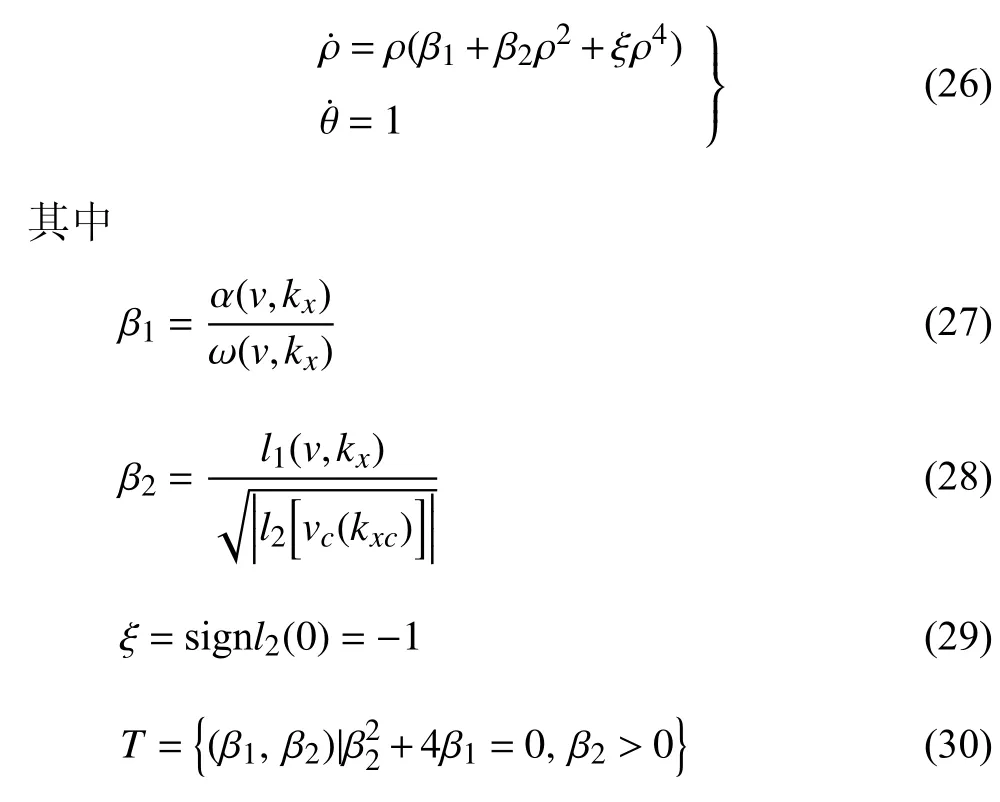
對應的Bautin 分岔見圖7,其中H?和H+分別對應Hopf 分岔的第一Lyapunov 系數(shù)小于0 和第一Lyapunov 系數(shù)大于0.

在圖7 中繞著Bautin 點逆時針方向考察,從區(qū)域①中的點開始,在該區(qū)域里面系統(tǒng)有單個穩(wěn)定平衡點而沒有極限環(huán).從區(qū)域①到區(qū)域②穿過Hopf 分岔邊界H?,出現(xiàn)唯一穩(wěn)定極限環(huán).當穿過Hopf 分岔邊界H+進入?yún)^(qū)域③時,該穩(wěn)定的極限環(huán)依然存在,此時平衡點恢復它的穩(wěn)定性,同時在第一個環(huán)內(nèi)部額外產(chǎn)生了一個不穩(wěn)定極限環(huán),兩個具有相反穩(wěn)定性的環(huán)在區(qū)域③中存在并在曲線T上相遇消失而留下單個穩(wěn)定平衡點,這就走完了一圈.

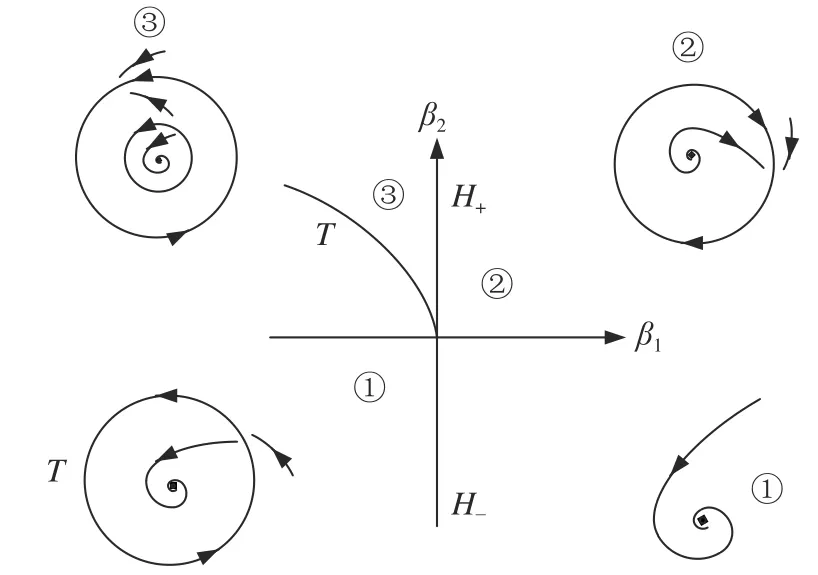
圖7 Bautin 分岔圖(ξ=?1)Fig.7 Bautin bifurcation diagram (ξ=?1)

在圖7 中每次穿越 β1軸時系統(tǒng)的第一Lyapunov 系數(shù)都會出現(xiàn)變號,若逆時針方向穿越 β1負半軸,系統(tǒng)從亞臨界Hopf 分岔轉(zhuǎn)變?yōu)槌R界Hopf 分岔,若逆時針穿越 β1正半軸,系統(tǒng)從超臨界Hopf 分岔轉(zhuǎn)變?yōu)閬喤R界Hopf 分岔.這就是系統(tǒng)在雙參數(shù)下,由亞臨界Hopf 分岔到超臨界Hopf 分岔,再從超臨 界Hopf 分岔到亞臨界Hopf 分岔的遷移轉(zhuǎn)化機理.

4.2 輪對系統(tǒng)考慮陀螺效應與不考慮陀螺效應時在退化Hopf 分岔點附近的Bautin 分岔拓撲圖對比

通過式(26)～ 式(30)中的坐標變化,得到考慮陀螺效應的輪對系統(tǒng)在運行速度與縱向剛度坐標系下的Bautin 分岔拓撲圖如圖8 所示.

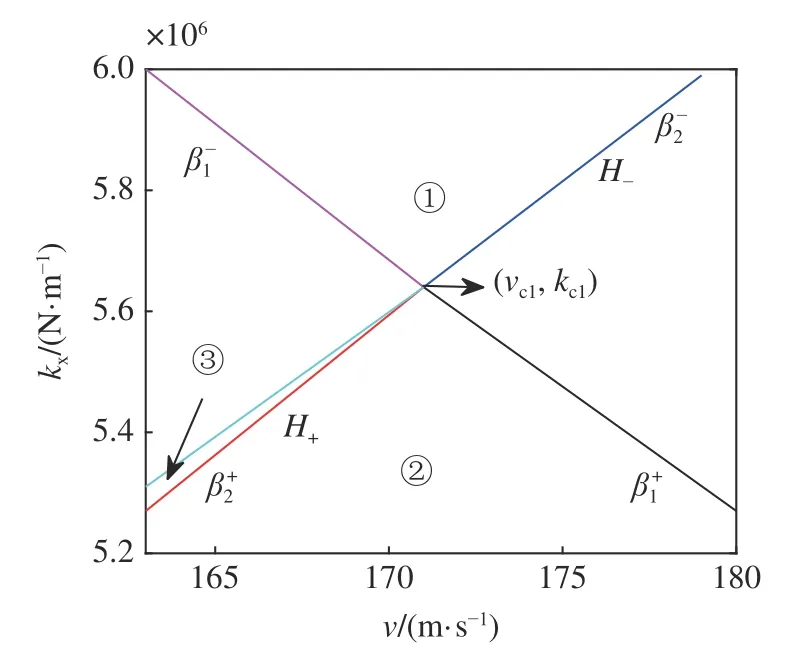
圖8 輪對系統(tǒng)考慮陀螺效應時的Bautin 分岔拓撲圖Fig.8 Bautin bifurcation topology diagram of wheelset system when considering gyroscopic action

系統(tǒng)中若存在穩(wěn)定的周期解,其相圖必然存在,在圖8 的區(qū)域①中取一個點(170 m/s,5.8 MN/m),在區(qū)域②中取一個點(170 m/s,5.2 MN/m),在區(qū)域③中取一個點(160 m/s,5.13 MN/m),在T曲線上取一個點(160 m/s,5544590 N/m),分別得到對應的相圖如圖9～ 圖12 所示.

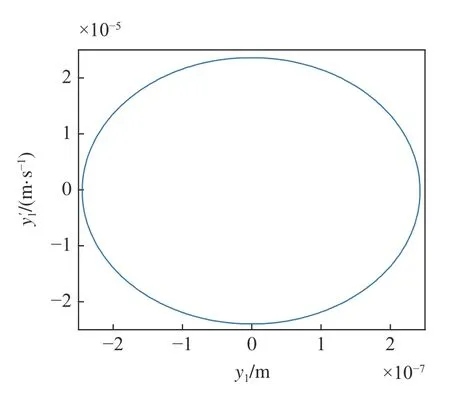
圖9 圖8 中區(qū)域①對應的相圖Fig.9 Phase diagram corresponding to area ①in Fig 8

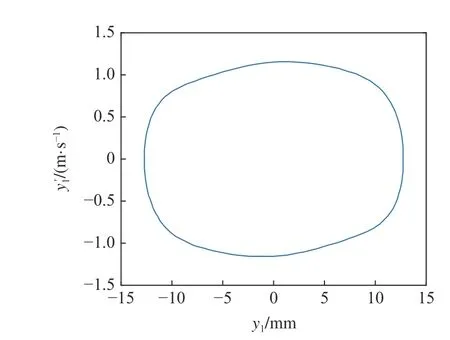
圖10 圖8 中區(qū)域②對應的相圖Fig.10 Phase diagram corresponding to area ② in Fig 8

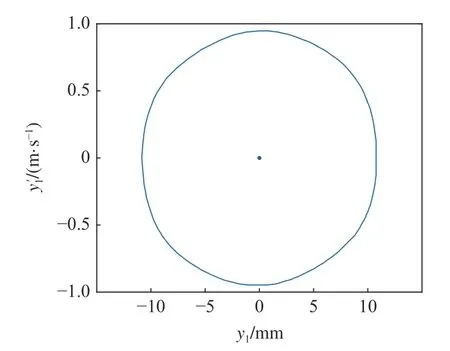
圖11 圖8 中區(qū)域③對應的相圖Fig.11 Phase diagram corresponding to area ③in Fig 8

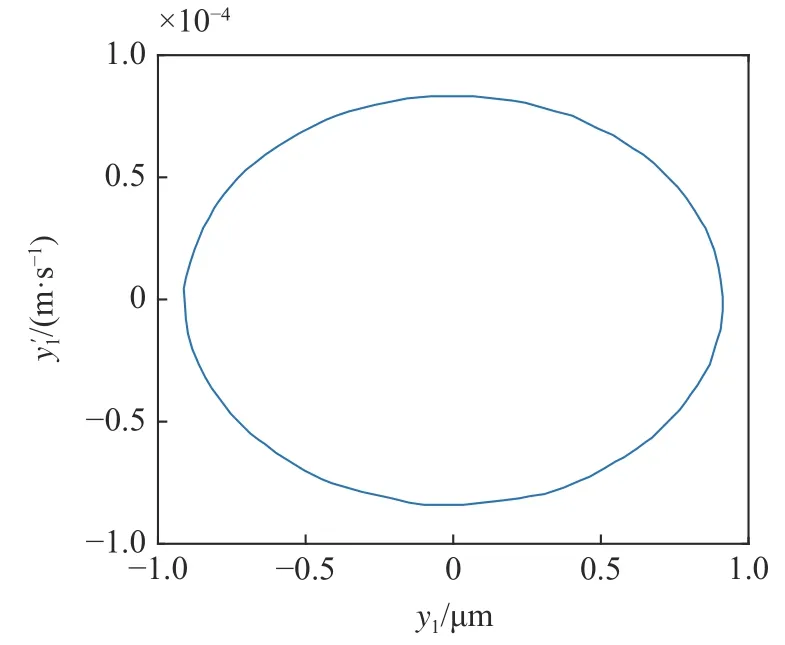
圖12 圖8 中T 區(qū)域?qū)南鄨DFig.12 Phase diagram corresponding to the T region in Fig 8

通過式(26)～ 式(30)中的坐標變化,得到不考慮陀螺效應的輪對系統(tǒng)在運行速度與縱向剛度坐標系下的Bautin 分岔拓撲圖如圖13 所示.

在圖13 的區(qū)域①中取點(170 m/s,6.5 MN/m),在區(qū)域②中取點(170 m/s,5.5 MN/m),在區(qū)域③中取點(160 m/s,5.54 MN/m),在T曲線上取點(160.3 m/s,5558921 N/m),分別得到對應的相圖如圖14～圖17 所示.

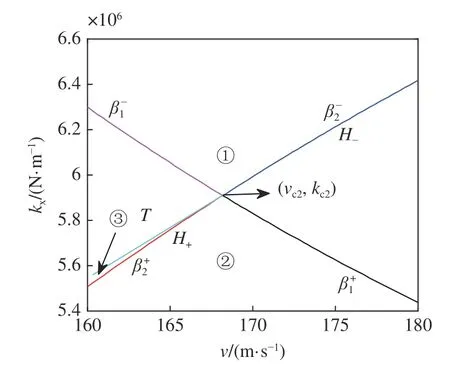
圖13 輪對系統(tǒng)不考慮陀螺效應時的Bautin 分岔拓撲圖Fig.13 Bautin bifurcation topology diagram of wheelset system without considering gyroscopic action

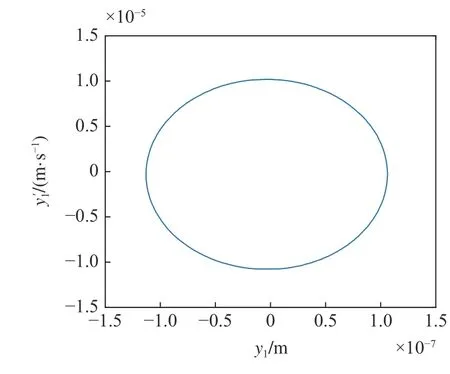
圖14 圖9 中區(qū)域①對應的相圖Fig.14 Phase diagram corresponding to area ①in Fig 9

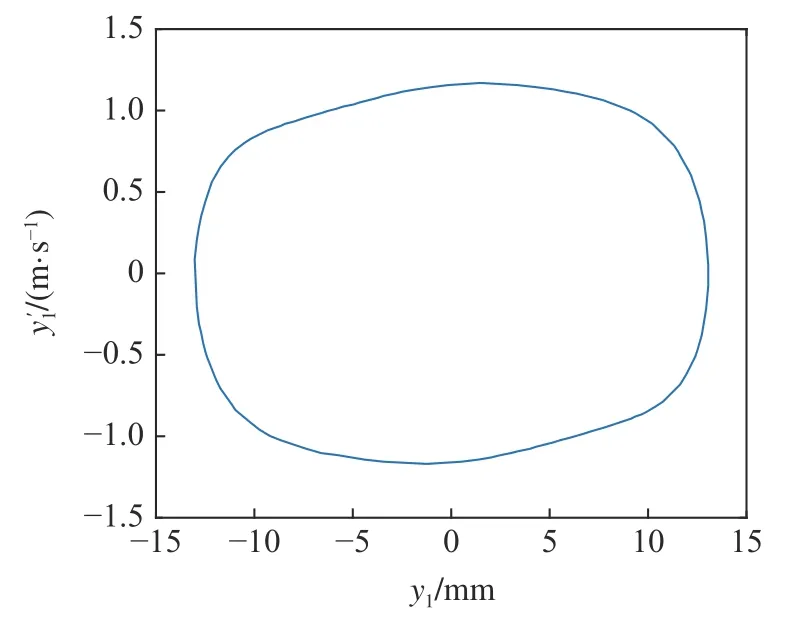
圖15 圖9 中區(qū)域②對應的相圖Fig.15 Phase diagram corresponding to area ② in Fig 9

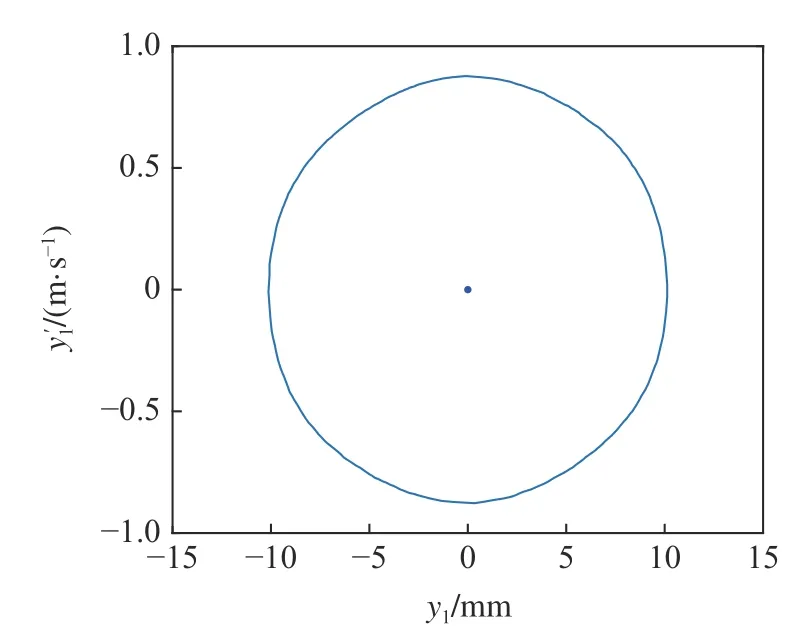
圖16 圖9 中區(qū)域③對應的相圖Fig.16 Phase diagram corresponding to area ③in Fig 9

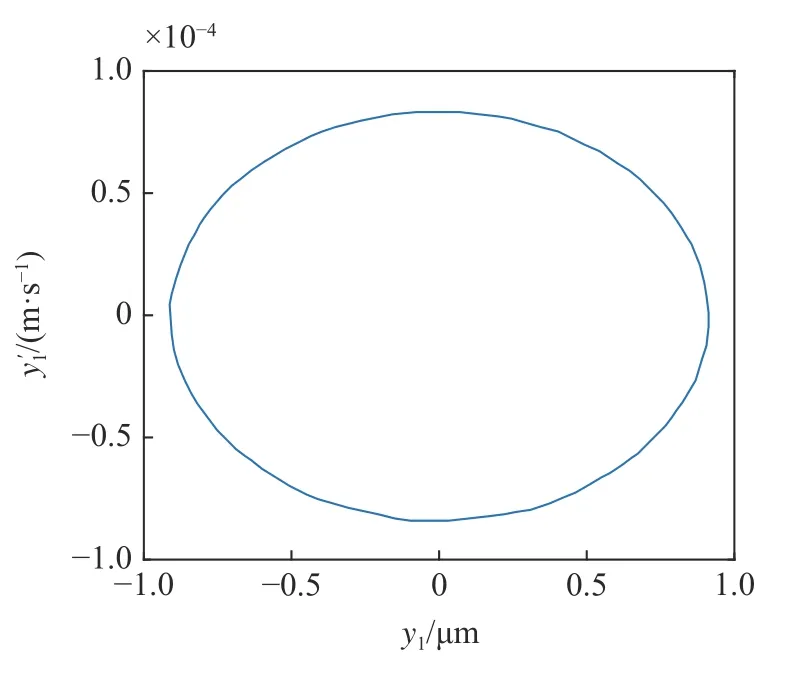
圖17 圖9 中T 區(qū)域?qū)南鄨DFig.17 Phase diagram corresponding to the T region in Fig 9

圖8 與圖13 分別展示了考慮陀螺效應與不考慮陀螺效應的輪對系統(tǒng)在退化Hopf 分岔點附近,依靠雙參數(shù)(縱向速度和縱向剛度)從亞臨界Hopf 分岔到超臨界Hopf 分岔,再從超臨界Hopf 分岔到亞臨界Hopf 分岔的轉(zhuǎn)化過程.

由圖9～ 圖12 可知,考慮陀螺效應的輪對系統(tǒng),其在退化Hopf 分岔點附近的Bautin 分岔拓撲圖的區(qū)域①中的點具有單個穩(wěn)定平衡點.區(qū)域②中的點具有單個穩(wěn)定極限環(huán).區(qū)域③中的點具有單個穩(wěn)定極限環(huán)和單個穩(wěn)定平衡點,T曲線上只有單個穩(wěn)定平衡點.該結(jié)論與圖7 中的理論結(jié)果是一致的.

由圖14～ 圖17 可知,不考慮陀螺效應的輪對系統(tǒng),其在退化Hopf 分岔點附近的Bautin 分岔拓撲圖的區(qū)域①中的點具有單個穩(wěn)定平衡點.區(qū)域②中的點具有單個穩(wěn)定極限環(huán).區(qū)域③中的點具有單個穩(wěn)定極限環(huán)和單個穩(wěn)定平衡點,T曲線上只有單個穩(wěn)定平衡點.該結(jié)論與圖7 中的理論結(jié)果是一致的.

由圖8～ 圖17 可知,陀螺效應將改變輪對系統(tǒng)的退化Hopf 分岔點,但對于在退化Hopf 分岔點附近的Bautin 分岔形式影響不大.

5 結(jié)論

本文基于Hopf 分岔代數(shù)判據(jù)、分岔理論和打靶法,分別得到考慮陀螺效應與不考慮陀螺效的輪對系統(tǒng)Hopf 分岔點解析表達式、在不同縱向剛度下的分岔圖和在退化Hopf 分岔點附近的Bautin 分岔拓撲圖.發(fā)現(xiàn)影響輪對系統(tǒng)陀螺效應的主要參數(shù)是輪對系統(tǒng)的橫向轉(zhuǎn)動慣量,次要參數(shù)是輪對系統(tǒng)的橫向自旋蠕滑系數(shù).陀螺效應不僅可以提高輪對系統(tǒng)的線性臨界速度,也可以提高輪對系統(tǒng)的非線性臨界速度,即陀螺效應對輪對系統(tǒng)的運動穩(wěn)定性具有增穩(wěn)作用.陀螺效應會改變輪對系統(tǒng)的退化Hopf 分岔點,但對退化Hopf 分岔點附近的Bautin分岔形式影響不大.

附錄A

附表 A1 輪對參數(shù)表Table A1 Wheelset parameter list

附表 A2 圖4 中各速度值Table A2 Values of each speed in Fig.4

附表 A3 圖5 中各速度值Table A3 Values of each speed in Fig.5

附表 A4 圖6 中各速度值Table A4 Values of each speed in Fig.6

附錄B