一種新的玻爾茲曼方程可計算模型構造與分析1)

彭傲平 李志輝 吳俊林 皮興才 蔣新宇

* (中國空氣動力研究與發展中心超高速空氣動力研究所,四川綿陽 621000)

? (北京航空航天大學國家計算流體力學實驗室,北京 100191)

引言

近年來,隨著對臨近空間戰略意義認識的加深,各航空航天大國發展了眾多臨近空間飛行器.為滿足長航時、大載荷、高超聲速巡航等需求,這類臨近空間飛行器通常整體尺寸較大,各部件間差異顯著,飛行過程會出現多物理多場耦合、多流區共存的多尺度復雜流動現象,傳統的數值模擬方法如基于宏觀連續介質假設的納維?斯托克斯(N-S) 方程、模擬微觀分子運動與碰撞的直接模擬蒙特卡洛(DSMC)方法難以滿足多尺度一體化模擬需求,需要研究發展新的模擬手段[1-4].本文從介觀氣體分子速度分布函數滿足的方程即玻爾茲曼方程[5-7]出發開展多尺度流動一體化模擬研究.

玻爾茲曼方程作為氣體動理學理論的基本方程,能描述各流域氣體流動輸運現象,但它是一個高度非線性的積分?微分方程,其理論解和直接數值求解均難以實現[7].為利用玻爾茲曼方程能統一描述各流域氣體流動的特性,眾多學者提出了系列替代求解技術,其中應用最廣泛的是模型方程方法,即用一個相對簡單的表達式替換玻爾茲曼方程碰撞積分項[8],再對簡化后的偏微分方程進行求解.

模型方程作為玻爾茲曼方程的近似,必須滿足玻爾茲曼方程的基本屬性,如總和不變量性質、H 定理、正確的輸運系數等.第一個也是最著名的模型方程是巴特納?格羅斯?克魯克模型[8](BGK模型),但通過對其進行查普曼?恩斯科(Chapman?Enskog)展開分析得到的普朗特數(Pr)為1,而單原子氣體的Pr約為2/3[9].為克服這一缺陷,國內外學者提出了一系列模型方程,包括橢球統計?BGK (ESBGK)模型[10-11]、沙克霍夫(Shakhov)模型[12-13]、劉(Liu)模型[14]、貝利(Belyi)模型[15]等,這些模型方程均假定其碰撞頻率與分子速度無關.此外,也有學者發展了考慮碰撞頻率與分子速度相關性的模型方程[16]以及適于多原子氣體、考慮熱力學非平衡的模型方程[17].

大量數學分析表明[16,18-20],上述模型方程均能滿足玻爾茲曼方程的基本屬性,且與原始玻爾茲曼方程的碰撞項具有類似的松弛特性,能保持與納維?斯托克斯方程、直接模擬蒙特卡洛方法的收斂一致,因結構簡單、貼近跨流域流體物理變化特點、可計算技術針對性強而得到廣泛應用[21],如泰塔雷夫(Titarev)建立了物理空間和速度空間均采用非結構網格的內斯韋塔依(Nesvetay)求解器[22-23],針對返回式空間飛行器等高馬赫數流動與直接模擬蒙特卡洛方法進行了系列對比分析.李志輝等[24-31]從研究描述各流域均適用的氣體分子速度分布函數方程出發,吸收計算數學指數型積分求解原理,發展了氣體分子運動論離散速度坐標法,研制經改進的高斯?埃爾米特積分方法等系列離散速度數值積分技術,消除氣體分子速度分布函數對速度空間的連續依賴性,將玻爾茲曼模型方程化為在各個離散速度坐標點處具有非線性源項的雙曲型守恒方程,基于計算流體力學數值求解技術,構造直接求解速度分布函數演化更新的氣體動理論數值格式和大規模并行計算策略,建立了氣體動理論統一算法(GKUA),開展了自由分子流到連續流復雜高超聲速氣動力/熱問題大規模并行計算及其在航天工程中的應用研究,同時對跨流域多體干擾流動問題、跨流域非定常流動問題進行了研究,獲得較好的成功.徐昆等[32-37]利用上述離散速度坐標法與BGK 類型格式相耦合,發展了統一氣體動理學格式(UGKS),使之適于模擬稀薄流到連續流氣體流動問題.

另一方面,從流動反映的物理現象來看,當流場中出現非平衡現象時,某點的速度分布函數已經不再是簡單的麥克斯韋平衡態分布,而是呈現各種形態,如雙峰分布、偏心分布等[38].這些分布與當地的氣體分子速度、流場宏觀速度、溫度以及熱流矢量、應力張量等宏觀輸運性質相關,這從玻爾茲曼方程的查普曼?恩斯科分析解[5,39]可以看出.因此在對玻爾茲曼方程碰撞積分進行物理分析、構造碰撞項的模型方程時應同時考慮這些因素,而常用的玻爾茲曼碰撞積分模型如沙克霍夫模型沒有考慮應力張量的影響,ES-BGK 模型屬于各向異性的類麥克斯韋分布,沒有考慮熱流矢量的影響.當模型方程不能全面反映這些因素時會導致模擬結果出現系統誤差,例如在稀薄過渡流區流動的克努森層內黏性效應占主導,應考慮應力張量的影響,沙克霍夫模型與直接模擬蒙特卡洛方法模擬結果存在較大差別[40].

為此,本文將從玻爾茲曼方程出發,基于查普曼?恩斯科漸近分析解[9]的數學推導,構造一種同時考慮熱流矢量和應力張量影響、滿足玻爾茲曼方程高階碰撞矩的綜合型可計算碰撞模型,并在數學上分析其基本屬性,建立與玻爾茲曼方程的聯系,給出新模型與現有模型方程的關系,同時基于碰撞動力學確定該可計算模型碰撞松弛參數表達式.最后在氣體動理論統一算法框架下,使用該新建玻爾茲曼方程可計算模型,通過模擬一維激波結構、二維近空間飛行環境平板和多體圓柱干擾流動來驗證新模型的有效性和可靠性.

1 模型方程的構造

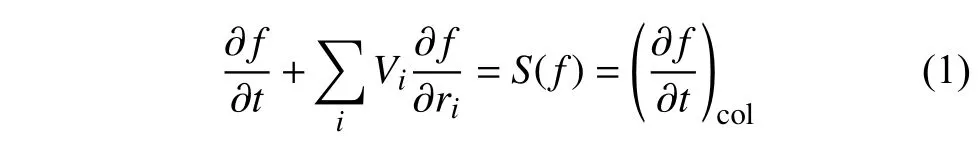
其中,i=x,y,z,Vx,Vy,Vz為氣體分子速度分量;x,y,z為空間位置坐標,t為時間;S(f),(?f/?t)col為碰撞積分項.

在確定速度分布函數f后,可以通過對其取矩得到宏觀流動參數,如密度 ρ,宏觀速度分量Ux,Uy,Uz,溫度T,應力張量分量Pij;熱流矢量分量qx,qy,qz分別為

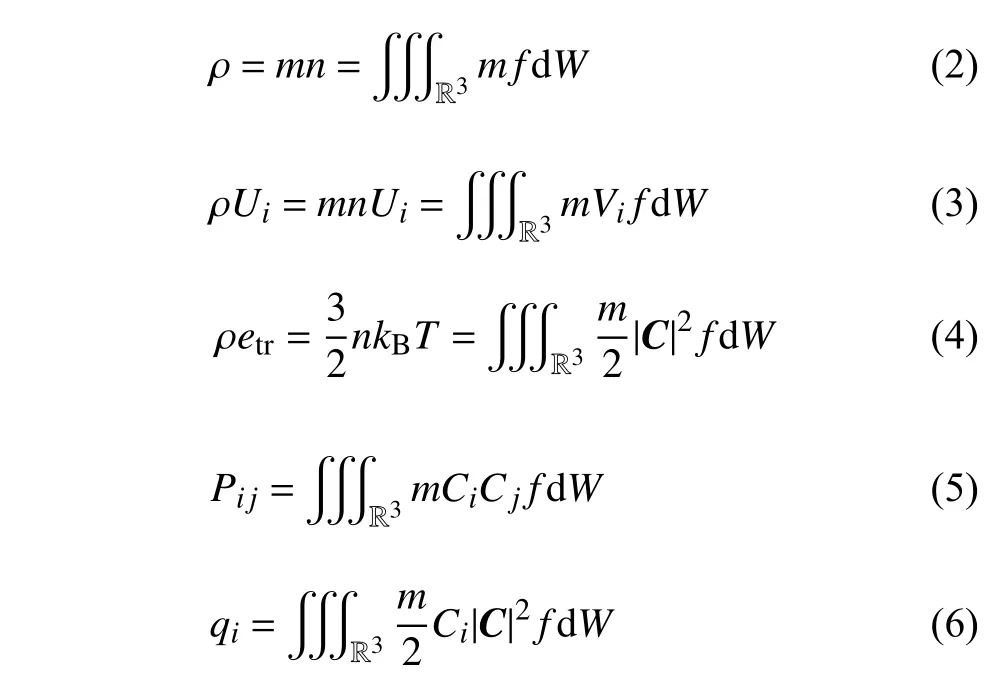
其中,R3為三維實數空間,dW=dVxdVydVz(下同),m為分子質量,n為分子數密度,kB為玻爾茲曼常數;i,j=x,y,z;C為分子熱運動速度,Ci=Vi?Ui,etr為單位質量動量.此外流場壓力p,黏性切應力張量分量 τij分別為

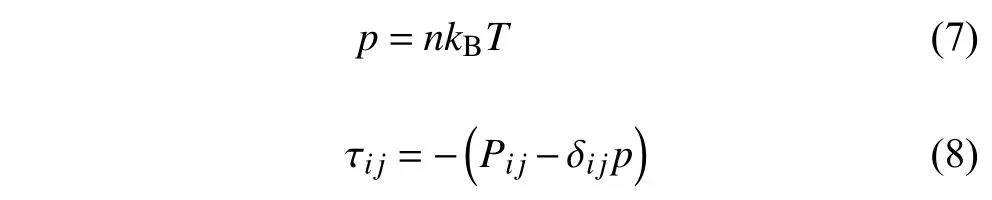
這里,符號 δij表示當i=j時為1,當i≠j時為0.

氣體動理論統一算法所用玻爾茲曼方程可計算模型[24-31]可以寫為

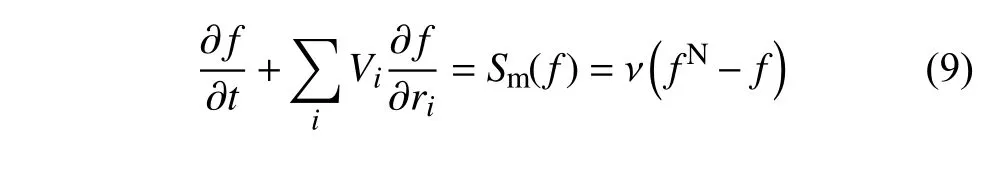
這里,ν 為氣體分子碰撞松弛參數,fN為當地平衡態速度分布函數.常用的沙克霍夫模型[12]和貝利模型[15]的表達式分別為

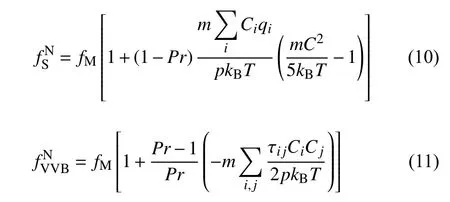
這里fM為麥克斯韋速度分布函數,即

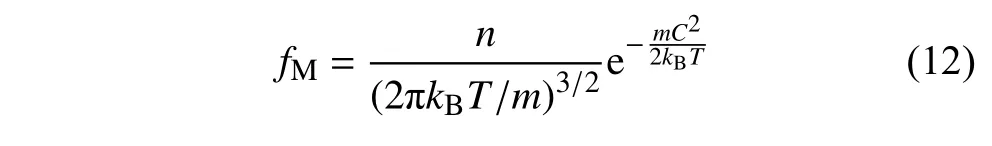
任何一個模型方程都必須滿足玻爾茲曼方程碰撞積分的如下3 個基本屬性[39].

(1)守恒性(質量、動量、能量守恒),即

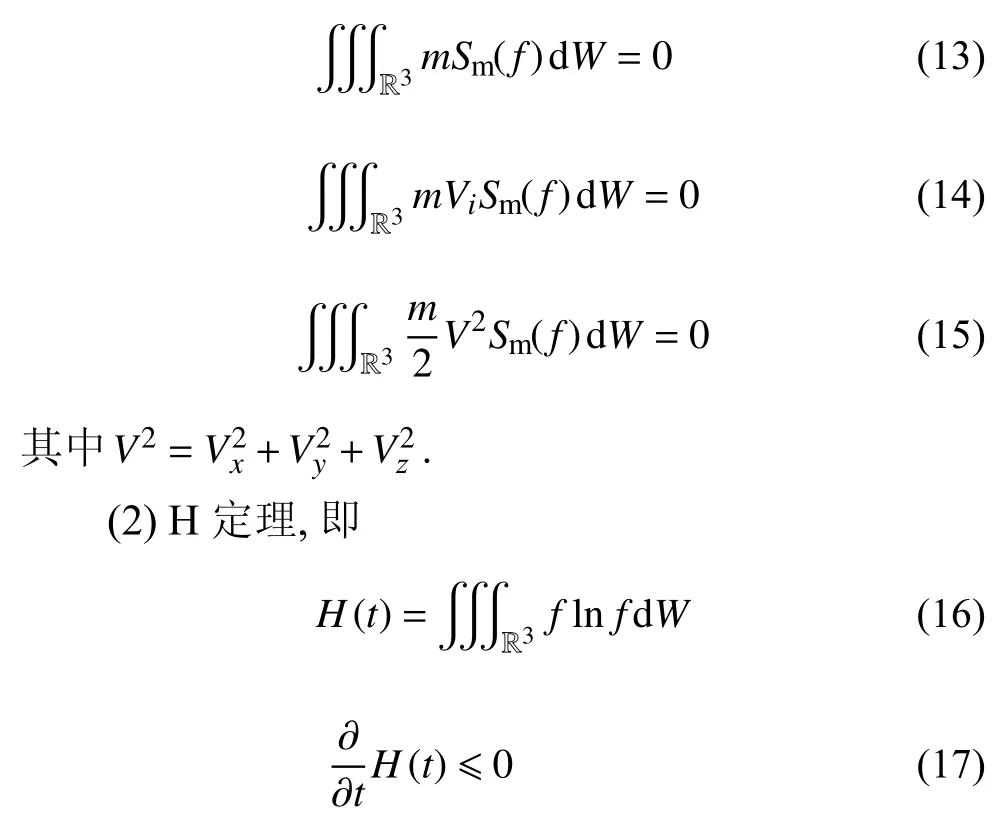
(3)在平衡態時,有Sm(fM)=0.

此外,對于單原子氣體,模型方程的查普曼?恩斯科分析得到的普朗特數Pr應約為2/3.

為研究構造新的玻爾茲曼方程可計算模型,首先分析其一階查普曼?恩斯科分析解[9],其可以寫為

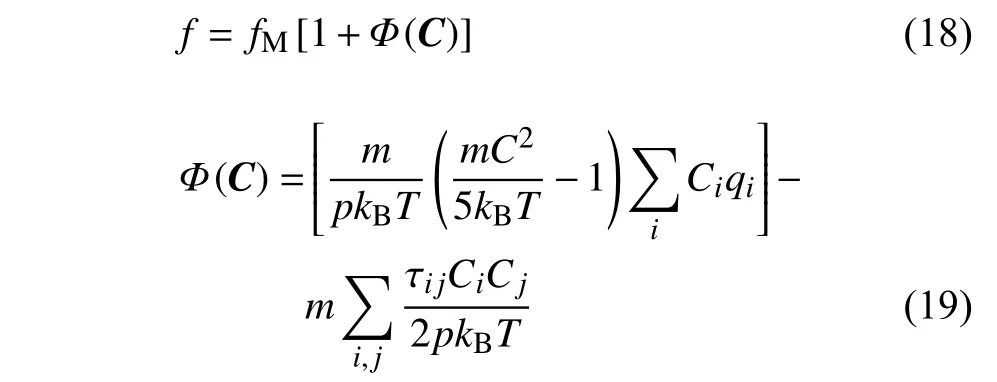
顯然,Φ (C)的第一項與常用的沙克霍夫模型[12]中第二項除系數外表達式一致,而 Φ (C)的第二項與貝利模型[15]的第二項除系數外表達式也一致.

從玻爾茲曼方程的查普曼?恩斯科分析解可以看出,流場中氣體的速度分布函數與局部宏觀流動參數如速度、熱流、應力等相關,而沙克霍夫模型沒有考慮應力的影響,貝利模型沒有考慮熱流的影響.當流場中局部區域的溫度、速度梯度較大即熱流和應力影響顯著時,將出現較為嚴重的非平衡效應,僅考慮單一因素難以準確模擬復雜非平衡現象.因此,可以依據玻爾茲曼方程的查普曼?恩斯科分析解以及常用模型方程的表達式,構造如下同時考慮熱流和應力影響的新型玻爾茲曼方程可計算模型

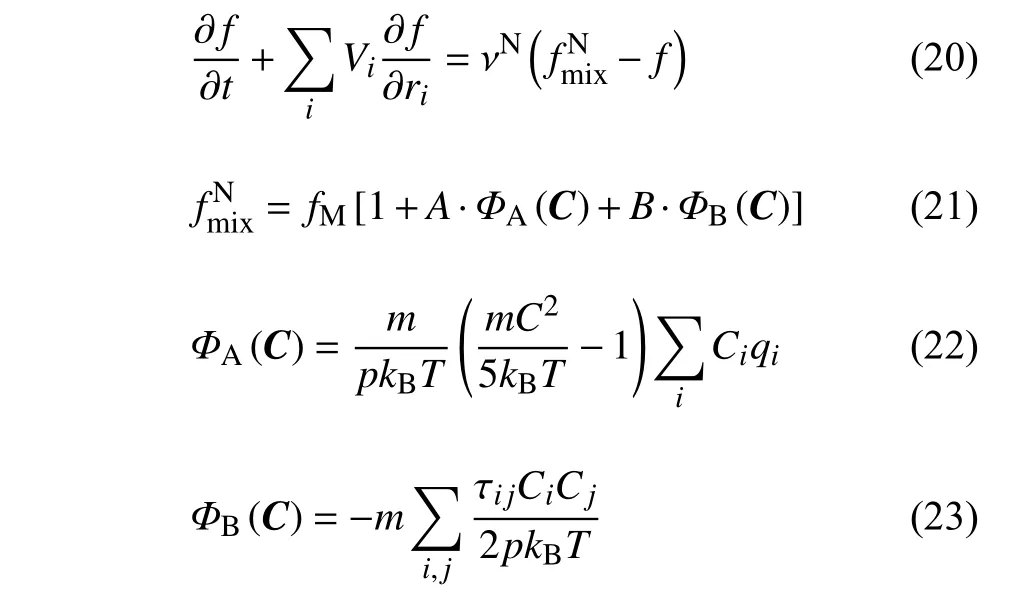
這里,A和B是與分子速度無關的常量,νN為碰撞松弛時間的倒數.顯然,當A=1?Pr,B=0時對應沙克霍夫模型[12],A=0,B=(Pr?1)/Pr時對應貝利模 型[15].

2 新型玻爾茲曼模型方程的數學分析

在構造玻爾茲曼方程的一個新模型后,需要對其性質進行分析,驗證其是否滿足玻爾茲曼方程碰撞積分項的基本屬性.

2.1 守恒性

由于

其中h=etr+p/ρ.上述3 個方程分別對應質量、動量和能量守恒方程.由此可知新模型方程滿足玻爾茲曼方程碰撞積分項的守恒性.

在平衡態時熱流和應力張量均為零,顯然此時當地麥克斯韋分布是模型方程的解.

2.2 查普曼?恩斯科分析

為開展查普曼?恩斯科分析,首先將新模型方程的無量綱形式寫成如下形式

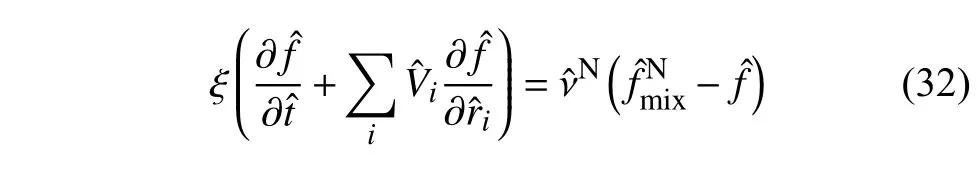
其中 ξ 為與來流克努森數(Kn)同量級的小量,頂標 ∧表示無量綱量.按查普曼?恩斯科分析的流程[9],定義

進而黏性系數 μ、熱傳導系數 κ、普朗特數Pr為

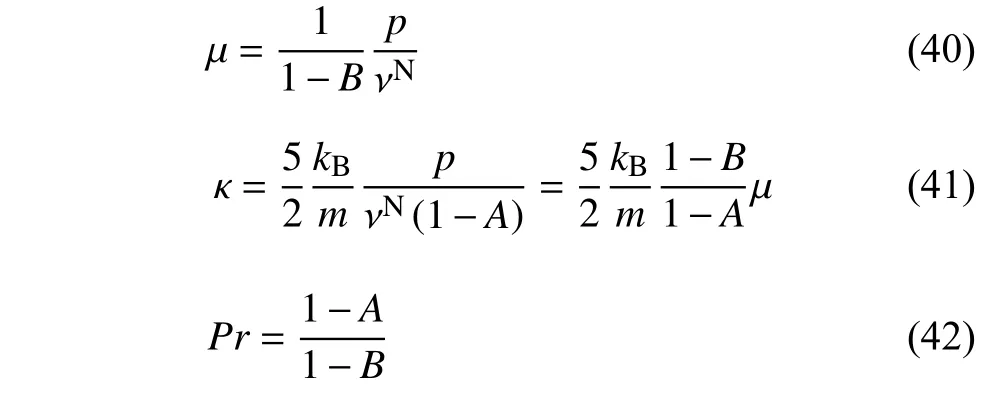
可知對于沙克霍夫模型[12],A=1?Pr,B=0,νS=p/μ ;對于貝利模型[15],A=0,B=(Pr?1)/Pr,νVVB=Pr·p/μ,這與前述一致.通過選擇合適的A,B可以得到正確的普朗特數Pr.

2.3 高階矩分析

為了進一步驗證新模型方程在數學上與玻爾茲曼方程的相容性,這里從麥克斯韋分子滿足的玻爾茲曼方程高階矩進行分析.由于麥克斯韋分子的特殊性,即其碰撞積分與相對速度無關,可以得到對應的高階矩.

定義碰撞積分項的矩為

該結論與上一節一致,這進一步證明了新模型方程與玻爾茲曼方程的相容性,與沙克霍夫模型[12]和貝利模型[15]的一致性.

2.4 H 定理的證明

定義[39]

且從查普曼?恩斯科分析的過程可知分布函數f相對fM的擾動為一小量,因此有

即當上述不等式成立,且Kn較小時,新模型方程滿足H 定理.從上面數學分析過程來看,νcoe在其取值范圍內可以任意選取,但在實際物理過程中即分布函 數的碰撞松弛中 νcoe需要具有一定的物理意義.

2.5 碰撞松弛參數的確定

在氣體動理學理論中,根據碰撞間隔理論[39]可以推導出碰撞時間間隔 η、黏性系數μ、壓力p之間的關系為

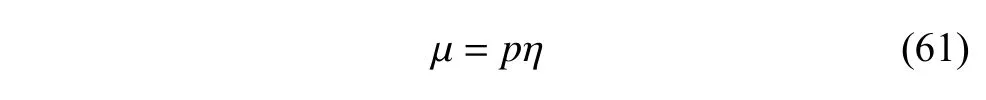
顯然,若將 η 直接視為玻爾茲曼模型方程中氣體分子碰撞松弛參數 ν 的倒數,則上式與沙克霍夫模型一致,對應于 νcoe=1.但上述碰撞間隔沒有考慮到分子碰撞后的速度殘留[39],因此需要對其進行修正,通常將其取為擾動馳豫時間,即

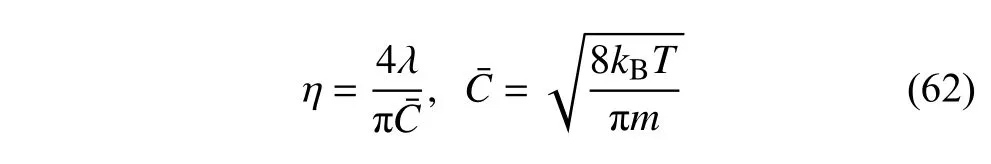
表征為分布函數松弛至其初始值的 1/e所歷經的時間(e 為自然對數的底),這里 λ 為平均自由程.

此外在直接模擬蒙特卡洛方法中,對于變徑硬球(VHS)模型有[41]

上述 νcoe是通過微觀分子碰撞間隔理論得到的,在氣體動理學介觀理論中,為了表征分布函數f松弛至的1/e 的物理意義,同時使 νcoe滿足式(60),本文針對新模型方程取

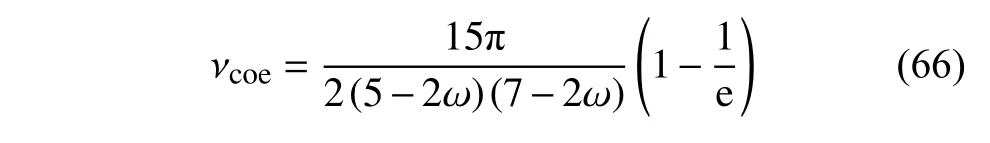
對于單原子氣體氬氣(Ar),ω=0.81,此時νcoe=0 .819;對于空氣,ω=0.77,νcoe=0.788 4.

3 數值分析

3.1 一維激波結構模擬分析

為驗證本文新建模型的有效性,首先模擬了一維激波結構.設置激波馬赫數為Mas=8,上游條件為:數密度n1=1 × 1023m?3,溫度T1=200 K,速度V1=2105.738 m/s;下游條件:n2=3.821 × 1020m?3,T2=4174.414 K,V2=551.111 m/s;氣體為氬氣;計算中激波上下游取當地平衡分布,空間網格間距取上游氣體分子平均自由程的0.05 倍.

圖1 給出了采用沙克霍夫模型、本文新建模型、貝利模型模擬的激波輪廓線與直接模擬蒙特卡洛方法結果的對比,分別用“Shakhov”“new model”“VVB”和“DSMC”表示,其中直接模擬蒙特卡洛方法結果由貝德(Bird)的一維可視化直接模擬(DS1V)代碼[41]計算得到,λ1表示激波上游氣體子平均自由程,并將密度輪廓 (ρ?ρ1)/(ρ2?ρ1)=0.5 置于x/λ1=0 處.圖2 給出了3 種模型模擬的一維激波內部無量綱熱流和切應力變化曲線.從圖1 可以看出本文新建模型能較好地反映Mas=8 的激波輪廓,驗證了其有效性;對于幾種模型而言,沙克霍夫模型與直接模擬蒙特卡洛方法結果符合最好,本文模型次之;差別主要在激波上游靠近x/λ1=0 區域,從圖2 可以看出該區域無量綱切應力 τxx變化很小,而無量綱熱流qx變化較大、且各模型結果區別也較大,僅考慮了熱流項的沙克霍夫模型與直接模擬蒙特卡洛方法結果最為接近,說明在一維激波內部宏觀切應力對內部參數分布影響很小,這可能是由于一維問題的宏觀切應力僅出現在x方向且無量綱值相對熱流較小,黏性效應不顯著.此外模型方程模擬的溫度輪廓在激波上游均出現了提前抬起的現象,這 可能是碰撞頻率與分子速度無關造成的.

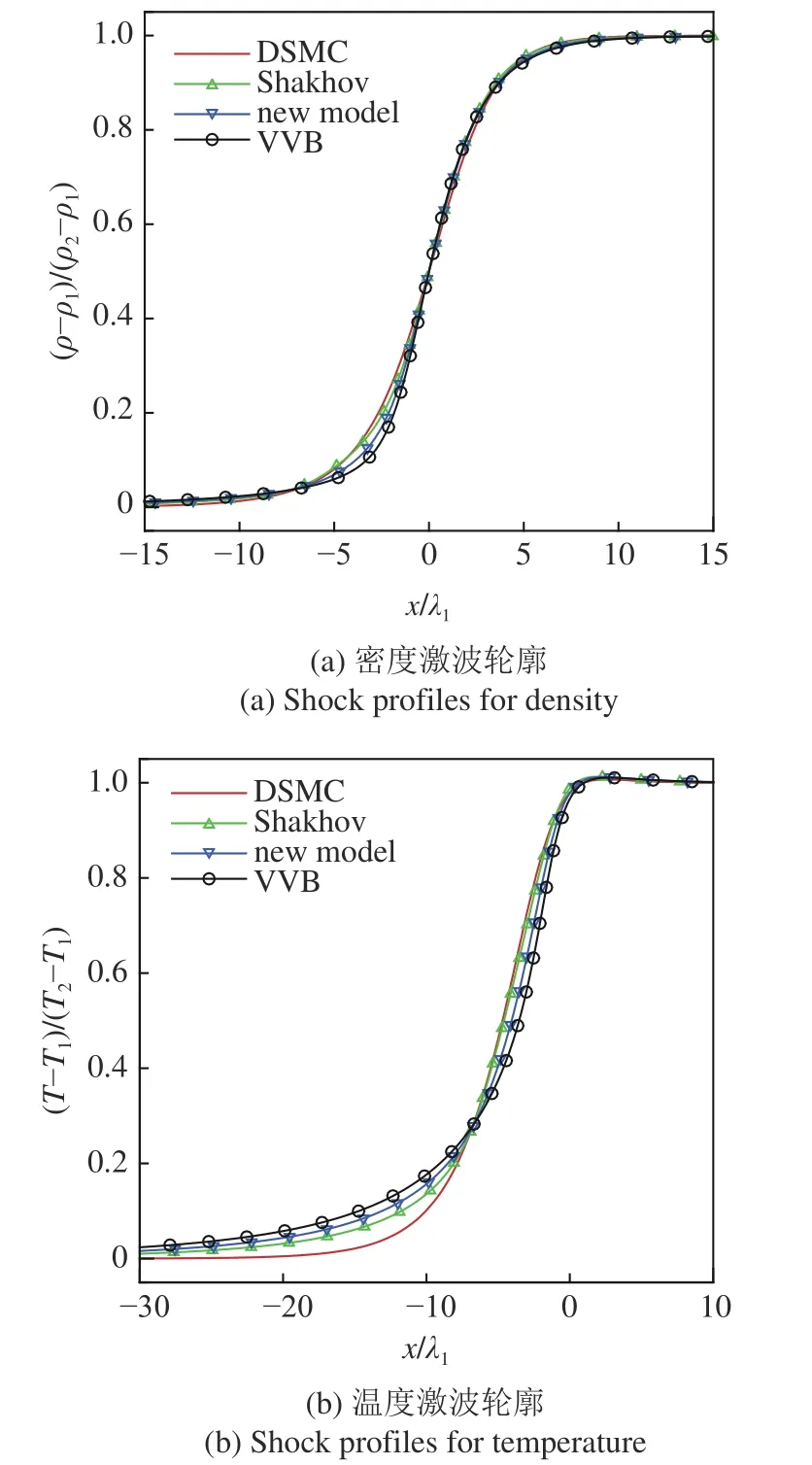
圖1 不同模型模擬的激波輪廓與直接模擬蒙特卡洛方法對比Fig.1 Comparison of shock profiles simulated by GKUA with different models and DSMC

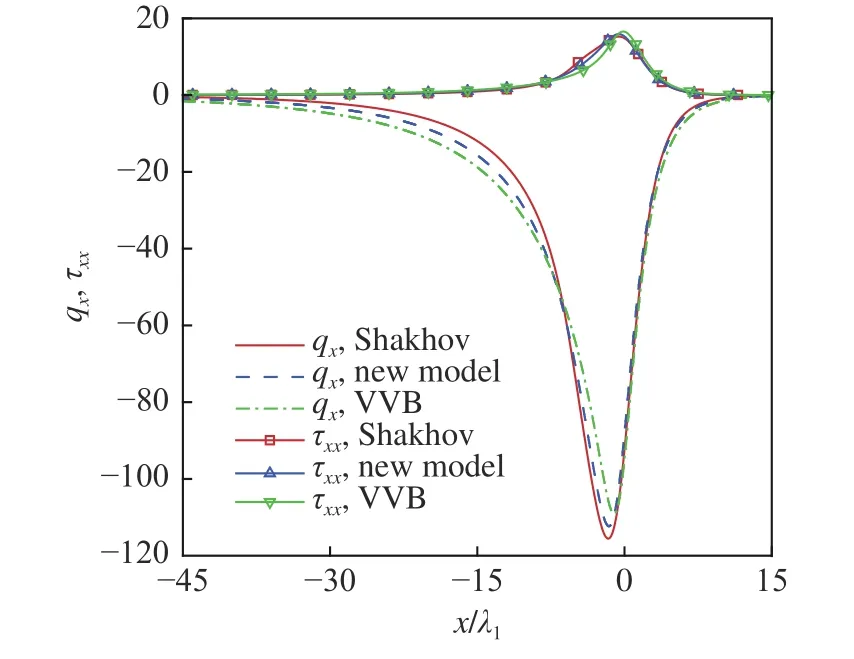
圖2 不同模型模擬的無量綱熱流和切應力對比Fig.2 Comparison of non-dimensional heat fluxes and shear stresses simulated by GKUA with different models

3.2 平板繞流模擬分析

為研究新模型方程模擬飛行器再入時在近空間環境黏性效應急劇增加的非平衡流場中黏性應力和熱流影響較大的區域流動問題,首先考察平板繞流.通常對于這類問題,在克努森層內越靠近平板前緣,溫度和速度梯度越大,非平衡效應越顯著,對應的熱流和黏性效應影響也越發嚴重.

來流條件:馬赫數Ma∞=5,來流氣體為氬氣,來流溫度和物面溫度均為200 K,數密度為n∞=1.175 × 1020m?3.平板長度為1 m、寬0.04 m.計算中,為了揭示高馬赫數附面層內流動與傳熱機制,直接模擬蒙特卡洛方法的背景網格間距取3.62 mm,統一算法貼近物面第一排網格間距為2.5 mm,均遠小于來流分子平均自由程10 mm.統一算法模擬中除了所用新、舊碰撞模型外其他計算條件完全一樣,物面采用與直接模擬蒙特卡洛方法一致的無穿透麥克斯韋散射分布,來流邊界為來流無量綱麥克斯韋平衡分布,出口邊界根據當地分子運動方向按特征邊界條件處理.圖3 給出了本文采用新模型方程模擬的溫度分布云圖(用GKUA_NewModel 表示的下半流場)與二維可視化直接模擬(DS2V)軟件[42]模擬結果(用DSMC 表示的上半流場)的對比情況.從圖中可以看出,兩個結果幾乎完全一致,而直接模擬蒙特卡洛方法尤其在尾部低速流場存在明顯的統計波動.這說明新模型模擬的流場結果是可信的.

圖3 本文模擬的溫度云圖與直接模擬蒙特卡洛方法結果對比Fig.3 Comparison of temperature contours simulated by GKUA with new model and DSMC

圖4 給出了在x=0.1 m 截面上壓力和溫度沿y方向不同碰撞模型的統一算法模擬結果與直接模擬蒙特卡洛方法的對比,其中本文建立的新模型用“new model”表示,沙克霍夫模型[12]用“Shakhov”表示,貝利模型[15]用“VVB”表示.從圖中可以看出,整體上使用新模型的統一算法結果與直接模擬蒙特卡洛方法模擬值相容,局部附面層區域y<0.15 m 時,相比沙克霍夫模型,新模型統一算法結果與直接模擬蒙特卡洛方法模擬值較為接近;而且還可看出對此黏性應力影響極為嚴重的附面層流動,使用貝利模型的統一算法結果與直接模擬蒙特卡洛方法模擬值符合更好;在0.15 m 0.225 m)流動處于近平衡態,直接模擬蒙特卡洛方法依靠麥克斯韋平衡態分布隨機采樣模擬分子的運動與碰撞,而統一算法基于求解當地氣體分子速度分布函數的演化更新實時捕捉宏觀流動量變化分布,使得不同模型得到的統一算法計算值較為一致,均與直接模擬蒙特卡洛方法模擬存在一定的偏差,反映出進一步發展求解玻爾茲曼模型速度分布函數方程的氣體動理論統一算法有其獨到新穎性與應用價值.

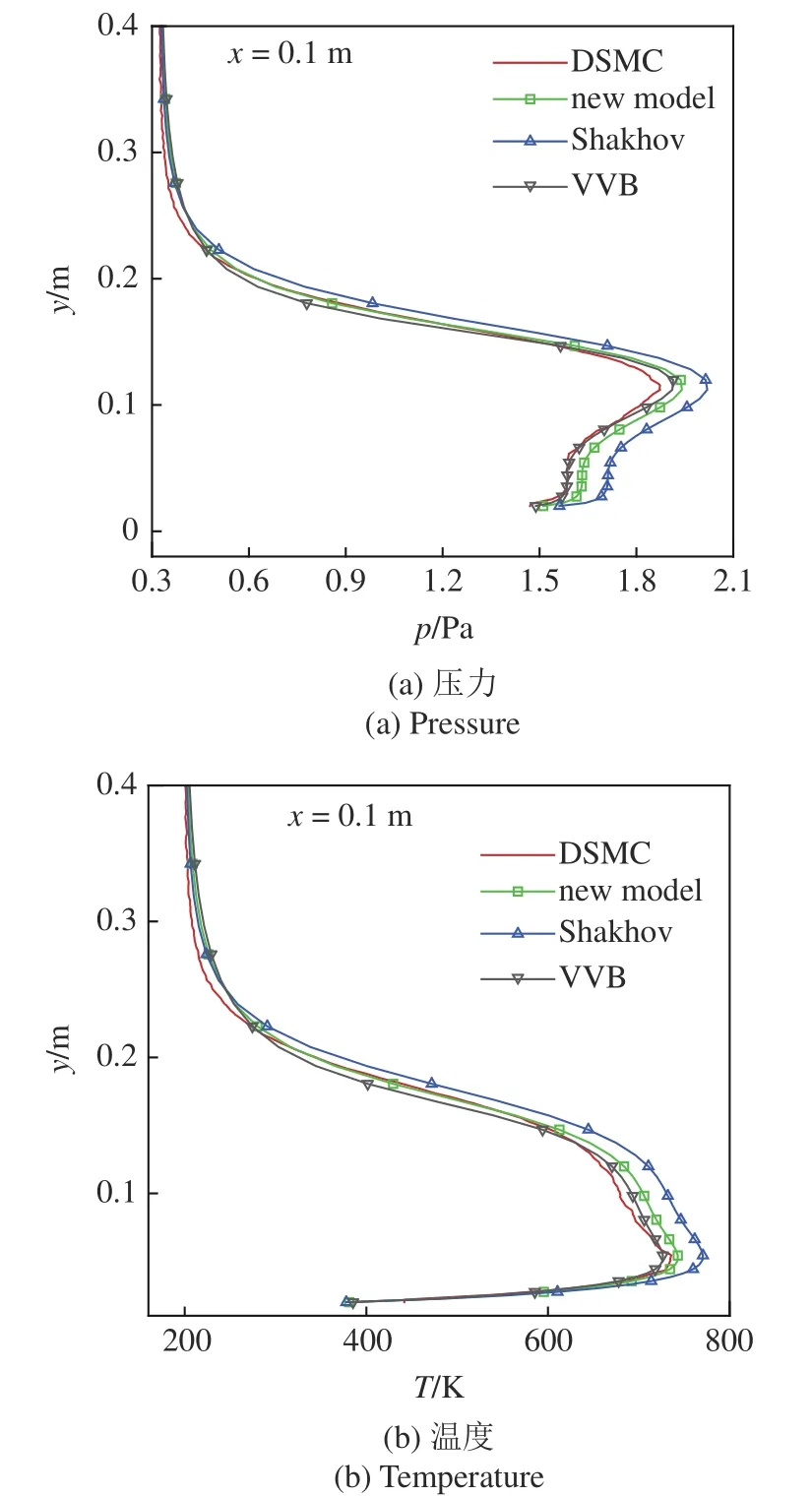
圖4 x=0.1 m 截面上壓力和溫度沿y 方向不同碰撞模型的統一算法計算值與直接模擬蒙特卡洛方法模擬結果的對比Fig.4 Comparison of pressure and temperature simulated by GKUA with different collision models and DSMC along the direction of y on the section of x=0.1 m

圖5 和圖6 分別給出了在x=0.5 m 和0.8 m 截面上壓力和溫度沿y方向不同碰撞模型的統一算法計算結果與直接模擬蒙特卡洛方法模擬值對比.隨著x增大剪切層范圍也擴大,在這些區域內流體黏性的影響較大,因而考慮了應力張量的碰撞模型,如使用3 種碰撞模型得到的統一算法計算分布變化趨勢彼此一致,尤其是貝利模型與本文新提出的模型方程統一算法計算分布近乎完全重合,能較好模擬這些區域的局部流動,整體上都與直接模擬蒙特卡洛方法模擬結果吻合.而當y增大到剪切層外緣時,熱流的影響開始顯現加劇的某些區域,使用沙克霍夫模型得到的統一算法結果更吻合直接模擬蒙特卡洛方法模擬值.同樣在當y進一步增大到遠離附面層臨近計算區域外緣,流動梯度仍然較大的近平衡態局部流場,幾種模型得到的統一算法計算值均與直接模擬蒙特卡洛方法模擬值存在一定的系統誤差,究其實質極可能緣于直接模擬蒙特卡洛方法完全使用麥克斯韋平衡態分布隨機統計模擬且存在統計漲落,導致了兩種方法體制的完全不一樣,對于流場梯度較大的局部流動模擬,彼此結果間存在一定的計算偏差.

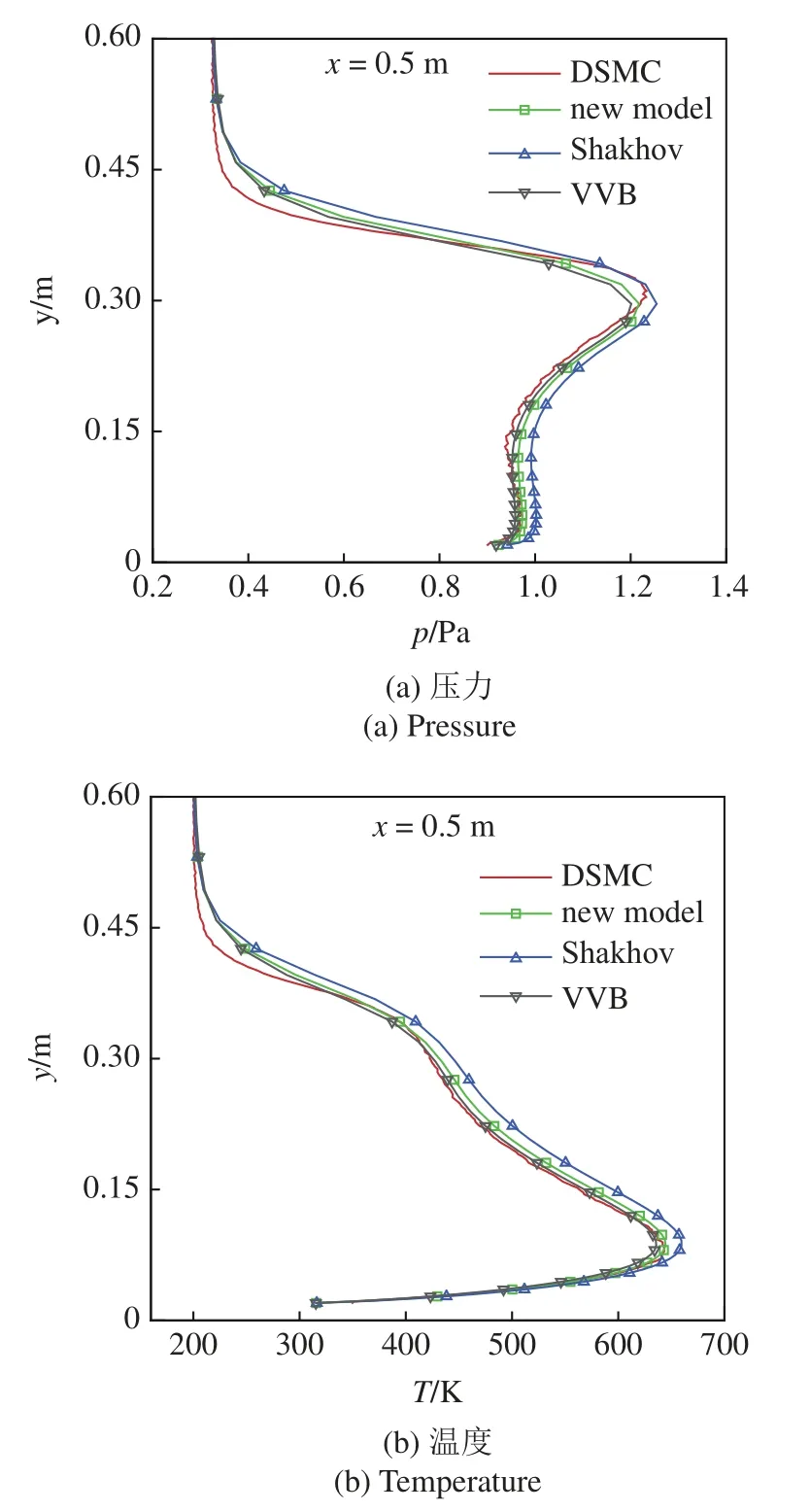
圖5 x=0.5 m 截面上壓力和溫度沿y 方向不同碰撞模型統一算法計算結果與直接模擬蒙特卡洛方法模擬值比較Fig.5 Comparison of pressure and temperature simulated by GKUA with different collision models and DSMC along the direction of y on the section of x=0.5 m

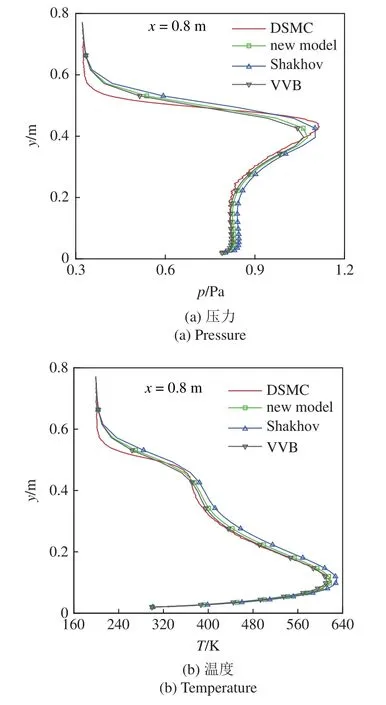
圖6 x=0.8 m 截面上壓力和溫度沿y 方向不同碰撞模型統一算法模擬結果與直接模擬蒙特卡洛方法的對比Fig.6 Comparison of pressure and temperature simulated by GKUA with different collision models and DSMC along the direction of y on the section of x=0.8 m

從圖4～ 圖6 可以看出,由于本文建立的玻爾茲曼方程新模型同時兼顧了流場中應力和熱流對氣體分子速度分布函數的影響,整體而言能較好地模擬全域流動.從統一算法計算x=0.1 m,0.5 m 和0.8 m 壓力和溫度變化來看,物面壓力從1.5 Pa 降至0.9 Pa和0.8 Pa,溫度從380 K 降至320 K 和300 K,相對于壁溫200 K,物面溫度跳躍逐漸降低,說明高馬赫數繞流平板前緣強壓縮流動在近空間飛行環境稀薄效應影響下逐漸變得稀疏,沿平板物面壓力、溫度不斷減小,過渡到平板尾部低壓常規流.

圖7 給出了駐點線上不同碰撞模型得到的統一算法計算溫度分布與直接模擬蒙特卡洛方法模擬值對比.平板頭部壓縮激波層是非平衡效應最為嚴重的區域,溫度梯度和速度梯度均較大.從圖中可以看出,在近空間飛行環境激波內部,本文建立的玻爾茲曼方程新模型統一算法計算結果始終與直接模擬蒙特卡洛方法模擬值符合較好.這進一步說明了需要同時考慮流場中黏性應力和熱流對氣體分子速度分布函數演化更新的影響.同時也看出基于玻爾茲曼方程可計算建模統一算法計算結果在駐點激波前部流動趨于近平衡態時溫度高于直接模擬蒙特卡洛方法模擬值,這與一維激波結構中溫度輪廓的變化規律類似.

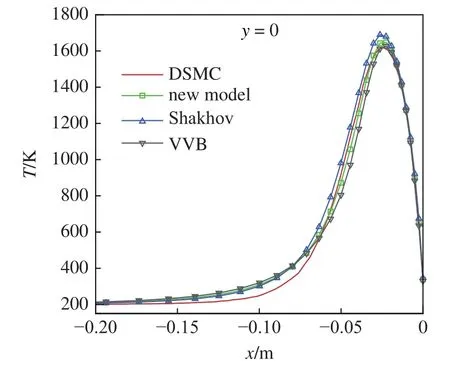
圖7 駐點線上不同碰撞模型統一算法計算的溫度分布與直接模擬蒙特卡洛方法模擬值比較Fig.7 Comparison of temperature simulated by GKUA with different collision models and DSMC along the stagnation line

3.3 雙圓柱干擾流動模擬分析

為驗證新建模型統一算法對激波干擾的模擬能力,這里考察雙圓柱干擾流動.來流條件和計算條件及邊界條件與上節一致,圓柱直徑為1 m,兩圓柱圓心間距為4 m.在該條件下上下兩個圓柱的頭部脫體激波會相互作用,形成復雜的激波干擾流動.

圖8 給出了分別使用3 種模型方程的統一算法計算溫度分布云圖與直接模擬蒙特卡洛方法模擬值的對比.兩圓柱脫體激波相互作用后在x=?0.19m 的位置形成一個正激波類馬赫桿,跨過馬赫桿后溫度和壓力增加、速度降低.而馬赫桿兩端形成的斜激波僅對圓柱尾流產生影響,將導致單邊圓柱法向力很小.從云圖可以看出,使用貝利模型統一算法得到核心區溫度分布與直接模擬蒙特卡洛方法模擬值最為接近,但馬赫桿位置稍向后,而沙克霍夫模型差別最大,對馬赫桿位置而言本文新建模型統一算法與直接模擬蒙特卡洛方法符合最好.表1 給出了3 種碰撞模型統一算法及直接模擬蒙特卡洛方法模擬得到的單邊圓柱軸向力系數及法向力系數,以及不同模型所得軸向力系數與直接模擬蒙特卡洛方法模擬結果的偏差.從表中可以看出,本文新建立的碰撞模型統一算法計算結果與直接模擬蒙特卡洛方法模擬值最大偏差在4.6%以內,能較好地模擬氣動力特性,精度優于常用的沙克霍夫模型.

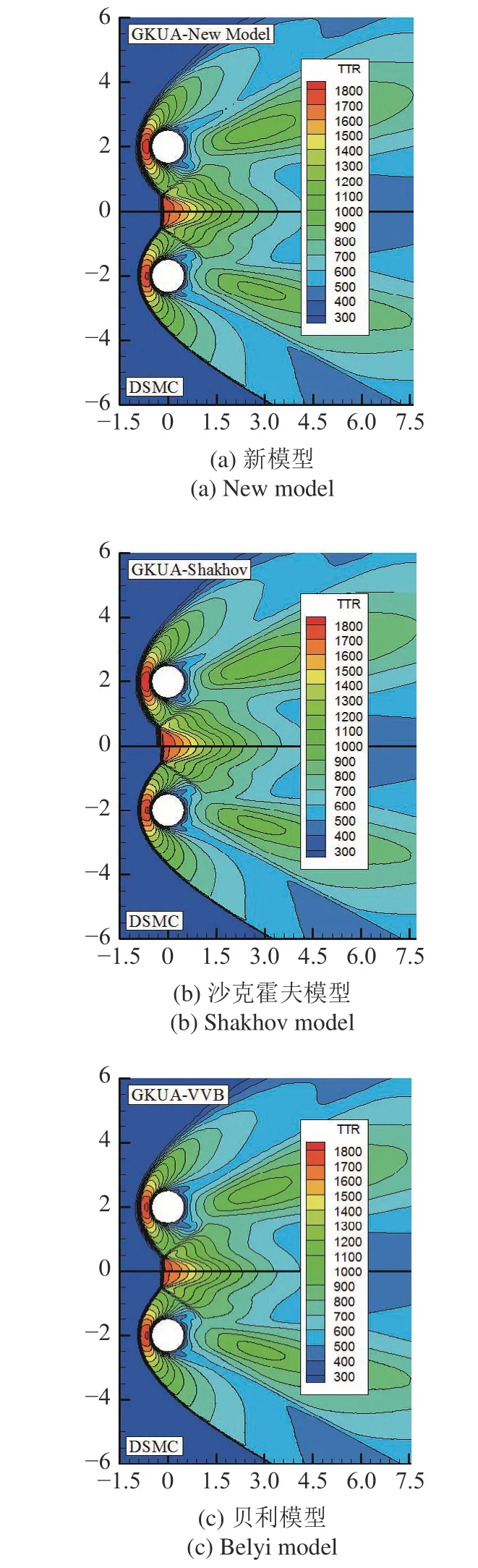
圖8 3 種模型方程計算得到的溫度分布云圖與直接模擬蒙特卡洛方法結果的對比Fig.8 Comparison of temperature contours simulated by GKUA with three collision models and DSMC

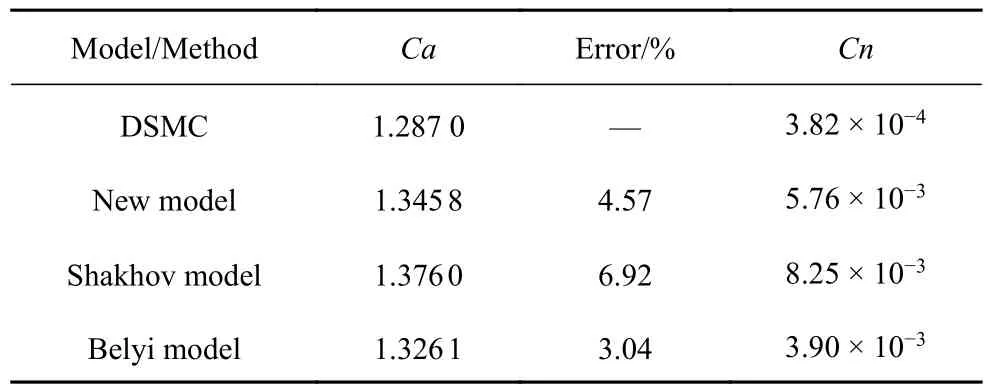
表1 不同模型/方法所得軸向力系數及其偏差與法向力系數Table 1 The axial and normal force coefficients by different models and DSMC method and errors between axial force coefficients

圖9 給出了對稱面(即y=0)上馬赫桿附近沿x方向不同碰撞模型統一算法計算得到的壓力、溫度和速度分布與直接模擬蒙特卡洛方法模擬值的對比情況.本文新建碰撞模型較好地求解了二維繞流的激波位置及激波前后宏觀參數的變化趨勢,明顯優于沙克霍夫模型,在激波內部模擬結果優于貝利模型.這是因為激波前后溫度和速度梯度較大,但y=0 截面上僅存在x方向熱流qx,而x和y方向的切應力 τxx和 τyy同時存在,速度梯度對分布函數的影響更大,使得本文新建碰撞模型能更好地模擬激波位置和內部參數變化.這與模擬一維激波結構所得結論不一致,可能是由于隨著維度的增加多方向宏觀切應力導致黏性效應更加顯著,其對分子速度分布函數的影響增大,與熱流共同作用影響激波位置 及其內部參數的分布.

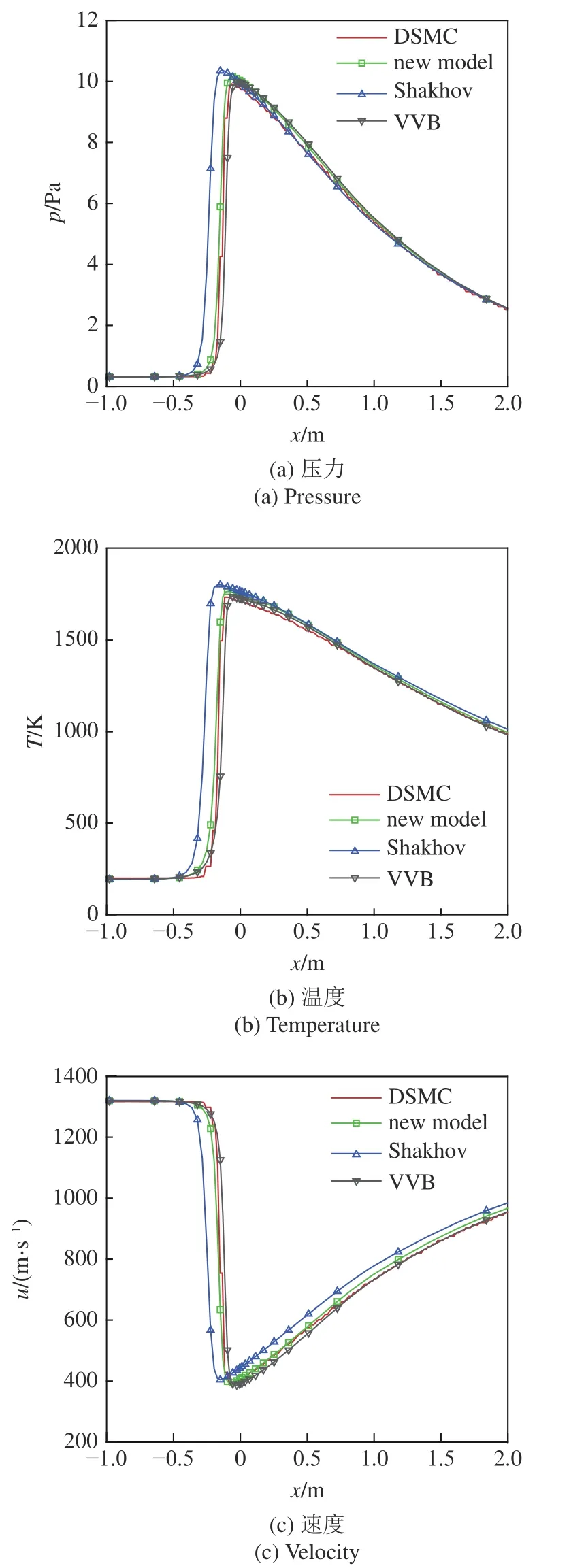
圖9 y=0 m 截面上壓力、溫度和速度沿 x 方向不同碰撞模型模擬結果與直接模擬蒙特卡洛方法的對比Fig.9 Comparison of pressure,temperature and velocity simulated by GKUA with different collision models and DSMC along the direction of x on the section of y=0 m

4 結論

本文通過分析玻爾茲曼方程的一階查普曼?恩斯科分析解,結合沙克霍夫模型和貝利模型構造過程及數學推導與物理分析,建立了一種同時考慮熱流矢量和應力張量影響、滿足玻爾茲曼方程高階碰撞矩的綜合可計算碰撞模型,并在數學上分析了其守恒性、H 定理等基本屬性,證明了新模型方程與玻爾茲曼方程的相容性,給出了新模型與現有模型的關系,通過碰撞動力學確定了碰撞松弛參數統一表達式.經過模擬一維激波結構、二維近空間飛行環境平板和多體圓柱干擾流動,并與直接模擬蒙特卡洛方法及不同碰撞模型方程的統一算法結果對比分析,得出以下結論:

(1)在稀薄效應顯著、非平衡現象突出的流動區域,熱流矢量和應力張量對當地氣體分子速度分布函數的影響較大,在構造碰撞松弛模型時需要同時考慮兩者的影響;

(2)在激波捕捉方面,流場中黏性效應顯著的區域沙克霍夫模型結果與直接模擬蒙特卡洛方法模擬值差別較大,本文新建模型與貝利模型結果接近,在激波內部本文模型與直接模擬蒙特卡洛方法符合更好,而在黏性效應較小時僅考慮熱流時結果與直接模擬蒙特卡洛方法符合更好,進一步說需要考慮多參數對分子速度分布函數的綜合影響;

(3)本文新建模型的碰撞松弛參數中引入了與自然對數的底 e 相關的常數作為自由參數,間接表征了分布函數松弛的物理意義,雖然能滿足模型方程的H 定理,但在流動的某些區域仍然與直接模擬蒙特卡洛方法存在差距.若能構造一個與當地非平衡參數相關聯的碰撞松弛參數,將氣體分子速度分布函數的松弛過程與當地流動參數的梯度耦合,應該能更好地模擬再入跨流域非平衡流動過程,這也是本文下一步擬開展的工作.