考慮層間摩擦接觸的瀝青路面模量反演分析

孫廣利 金 辰

(1.內(nèi)蒙古公路交通投資發(fā)展有限公司 呼和浩特 010000；2.同濟大學道路與交通工程教育部重點實驗室 上海 201804)

采用落錘式彎沉儀(FWD)合理地反演半剛性基層瀝青路面模量對路面結(jié)構(gòu)承載能力評價具有重要意義。然而，目前國內(nèi)外的模量反演方法大多是在彈性層狀連續(xù)體系基礎(chǔ)上建立的，沒有充分考慮結(jié)構(gòu)層間非連續(xù)接觸條件，導致反演結(jié)果無法客觀反映結(jié)構(gòu)層實際情況。邱欣[1]系統(tǒng)分析了層間非連續(xù)接觸條件對路面模量反演結(jié)果的影響，發(fā)現(xiàn)層間非連續(xù)接觸對面層和土基的反演結(jié)果影響不大，而使基層模量反演結(jié)果顯著偏低，反演值是理論值的40%～43%。查旭東[2]、楊國良[3]、朱潔[4]等分別基于同倫方法、神經(jīng)網(wǎng)絡(luò)法、迭代法等優(yōu)化算法，提出了路面模量反演方法，但研究過程缺乏對實際層間接觸條件的考慮。近年來，由于DBP法能夠有效避免傳統(tǒng)方法中解不唯一、初始值和局部收斂的問題，而得到了長足發(fā)展。所謂DBP法是建立彎沉盆參數(shù)(deflection basin parameters,DBP)與結(jié)構(gòu)層模量的相關(guān)關(guān)系，從而利用DBP反演結(jié)構(gòu)層模量。楊國良[5]、Rabbi[6]等采用DBP方法對路面結(jié)構(gòu)層性能狀況進行了預估評價，但研究過程忽略了層間非連續(xù)接觸條件的影響，且沒有充分考慮FWD荷載的動力效應(yīng)。

為此，本文基于層間非連續(xù)接觸條件，充分考慮FWD荷載的動力效應(yīng)，建立三維動力有限元模型，構(gòu)建路表彎沉盆與各結(jié)構(gòu)層模量對應(yīng)數(shù)據(jù)庫。以數(shù)據(jù)庫為基礎(chǔ)，進行DBP敏感性分析，并利用多元回歸分析方法提出結(jié)構(gòu)層模量反演回歸模型。

1 半剛性基層瀝青路面三維動力有限元模型

1.1 路面結(jié)構(gòu)及材料參數(shù)

選用我國常用的半剛性基層瀝青路面結(jié)構(gòu)層厚度組合，考慮到FWD沖擊荷載作用持續(xù)時間較短，將各結(jié)構(gòu)層視為線彈性體。根據(jù)JTG D50-2017《公路瀝青路面設(shè)計規(guī)范》中推薦的路面材料模量取值范圍及王旭東[7]對路面材料模量的室內(nèi)試驗結(jié)果，各結(jié)構(gòu)層的厚度及材料參數(shù)取值見表1。

表1 常見半剛性基層瀝青路面結(jié)構(gòu)參數(shù)取值范圍

1.2 FWD荷載與動力分析

參考國內(nèi)外文獻，通常采用半正弦曲線描述FWD產(chǎn)生的沖擊荷載，見式(1)，荷載峰值pmax為0.707 MPa，荷載作用周期T為0.03 s，荷載作用半徑為15 cm。

(1)

由于FWD荷載屬于脈沖式荷載，荷載作用時間很短，應(yīng)采用動力分析方法。同時，考慮到隱式動力分析的數(shù)值穩(wěn)定性更好，且對道路結(jié)構(gòu)動力響應(yīng)問題更為有效[8]，故采用隱式動力分析方法來分析FWD荷載作用下的路面響應(yīng)。具體分析時，還需提供用于計算阻尼矩陣的瑞利阻尼系數(shù)。本文根據(jù)國內(nèi)外學者的研究成果，各結(jié)構(gòu)層所選用的瑞利阻尼系數(shù)見表1。

1.3 路面層間接觸條件

路面結(jié)構(gòu)層之間的接觸狀態(tài)主要有完全黏結(jié)、部分黏結(jié)和完全光滑3種。在采用ABAQUS分析路面響應(yīng)時，國內(nèi)外通常采用Tie接觸來模擬層間完全黏結(jié)狀態(tài)；采用庫侖摩擦模型來模擬層間部分黏結(jié)或完全光滑狀態(tài)，并通過摩擦系數(shù)控制層間滑移行為，摩擦系數(shù)越大，層間黏結(jié)越好，摩擦系數(shù)為0時，代表層間完全光滑。

本文模型涉及2對接觸面：①面層與基層接觸面；②基層與土基接觸面。對于面層與基層接觸面，由于瀝青面層與半剛性基層材料差異較大，在交通荷載和環(huán)境反復作用下，面層與基層之間的黏結(jié)作用會逐漸減弱，且大量路面調(diào)查表明，面層與基層之間層間脫開現(xiàn)象較多，層間黏結(jié)作用較弱。因此，采用庫侖摩擦模型來模擬面層與基層之間的部分黏結(jié)狀態(tài)。參考國內(nèi)外學者在構(gòu)建路面有限元模型時的摩擦系數(shù)取值，本文摩擦系數(shù)取為0～1[9-11]。對于基層與土基接觸面，由于荷載尤其是引起水平向相對滑移的荷載隨深度逐漸減小，可認為層間為連續(xù)的變形和滑移，故采用Tie接觸來模擬基層與土基之間的完全黏結(jié)狀態(tài)。

1.4 模型尺寸與網(wǎng)格劃分

由于瀝青路面的各結(jié)構(gòu)層在水平方向無限伸展，底層在深度和水平方向無限伸展，且FWD的荷載作用區(qū)域具有對稱性，故可采用1/4對稱模型進行分析。經(jīng)試算，最優(yōu)模型長和寬取為5 m×5 m，路基深度方向取為8 m。模型底部采用固定約束，水平方向約束法向位移，對稱面施加對稱邊界條件。模型采用C3D8R三維六面體單元進行模擬。考慮到彎沉盆測點距荷載中心的距離分別為0，20，30，45，60，90，120，150，180 cm，為方便通過節(jié)點直接獲取FWD各傳感器位置上的彎沉值，在靠近受荷位置的區(qū)域網(wǎng)格劃分尺寸為5 cm。同時考慮計算精度和計算效率，在遠離受荷位置的區(qū)域網(wǎng)格劃分相對較粗。整個結(jié)構(gòu)的三維動力有限元模型的示意圖見圖1。圖中d1～d9分別代表0～180 cm位置處的9個傳感器。

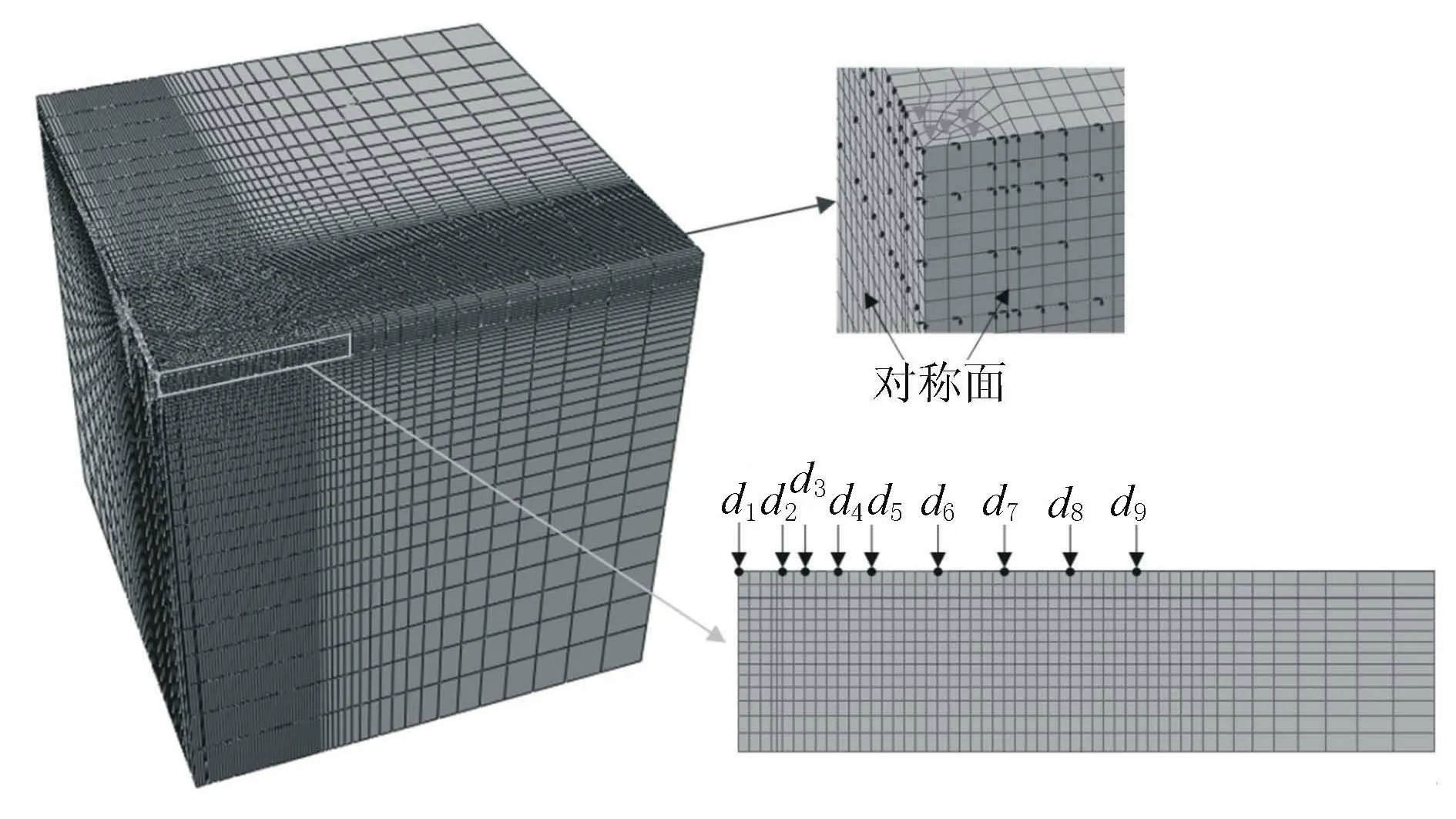
圖1 三維動力模型示意圖

1.5 有限元模型驗證

邱欣利用FWD測試設(shè)備對上海滬寧高速公路進行了路表彎沉測試，獲取了實測彎沉盆數(shù)據(jù)，并測試得到了結(jié)構(gòu)層模量、層間摩擦系數(shù)等相關(guān)數(shù)據(jù)。相同路面結(jié)構(gòu)工況下現(xiàn)場測試與本文數(shù)值模擬的對比結(jié)果見表2。

表2 實測彎沉數(shù)據(jù)與計算彎沉數(shù)據(jù)對比

由表2可見，兩者的均方根誤差RMSE在3.4%～6.2 %之間，結(jié)果相近。因此，可基于本文的建模方法，進一步開展瀝青路面模量反演分析。

2 數(shù)據(jù)庫構(gòu)建與DBP指標敏感性分析

2.1 數(shù)據(jù)庫構(gòu)建

根據(jù)本文所述的建模方法與表1中的路面結(jié)構(gòu)組合形式與材料參數(shù)，共對21種路面結(jié)構(gòu)組合進行計算。瀝青面層模量為2 000～22 000 MPa，步長取為4 000 MPa；半剛性基層模量為3 000～23 000 MPa，步長取為4 000 MPa；土基模量為100～400 MPa，步長取為100 MPa；層間摩擦系數(shù)取為0或1。故每種路面結(jié)構(gòu)組合對應(yīng)288種工況，本文共計算了6 048種工況，并以此構(gòu)建路表彎沉盆與各結(jié)構(gòu)層參數(shù)之間的對應(yīng)數(shù)據(jù)庫。

2.2 DBP的敏感性分析

為準確評價路面性能狀態(tài)，國內(nèi)外研究者提出了各種不同的DBP指標，總結(jié)概括為7類見表3。表中d1～d9分別為0～180 cm位置處的9個傳感器的彎沉值，0.001 mm；r1～r9分別為9個傳感器距荷載中心的距離，cm。

表3 彎沉盆參數(shù)指標

為探究面層模量Eac、基層模量Ebc、土基模量Esg對上述DBP指標的影響程度，本文以敏感度系數(shù)作為評價指標進行了敏感性分析。敏感度系數(shù)(SAF)的計算方法見式(2)，敏感度系數(shù)越大，表明兩變量之間越敏感。

(2)

式中：ΔA/A為彎沉盆參數(shù)的變動比率；ΔF/F為結(jié)構(gòu)層模量的變動比率。

按敏感度系數(shù)由大到小進行排序，綜合分析結(jié)果見表4。

表4 彎沉盆參數(shù)敏感度系數(shù)綜合排序

由表4可見，對面層模量變化較敏感的彎沉盆參數(shù)依次為：DD2>CI3>S1；對基層模量變化較敏感的彎沉盆參數(shù)依次為：CI2>S2>DD5；對土基模量變化較敏感的彎沉盆參數(shù)依次為：d9>CI8>S7，可利用敏感性較強的彎沉盆參數(shù)反演各結(jié)構(gòu)層模量。

3 各結(jié)構(gòu)層模量反演回歸模型

基于DBP敏感性分析結(jié)果，選取對面層模量變化較敏感的DBP指標，通過多元非線性回歸分析，建立了特定面層和基層厚度下，面層模量反演回歸模型，見式(3)。

lnEac=aln(DD2)+bln(CI3)+clnS1+d

(3)

式中：Eac為面層模量，MPa；DD2、CI3、S1為彎沉盆參數(shù)指標；a、b、c、d為回歸系數(shù)。

不同路面結(jié)構(gòu)組合下，模型所對應(yīng)的擬合結(jié)果見表5。

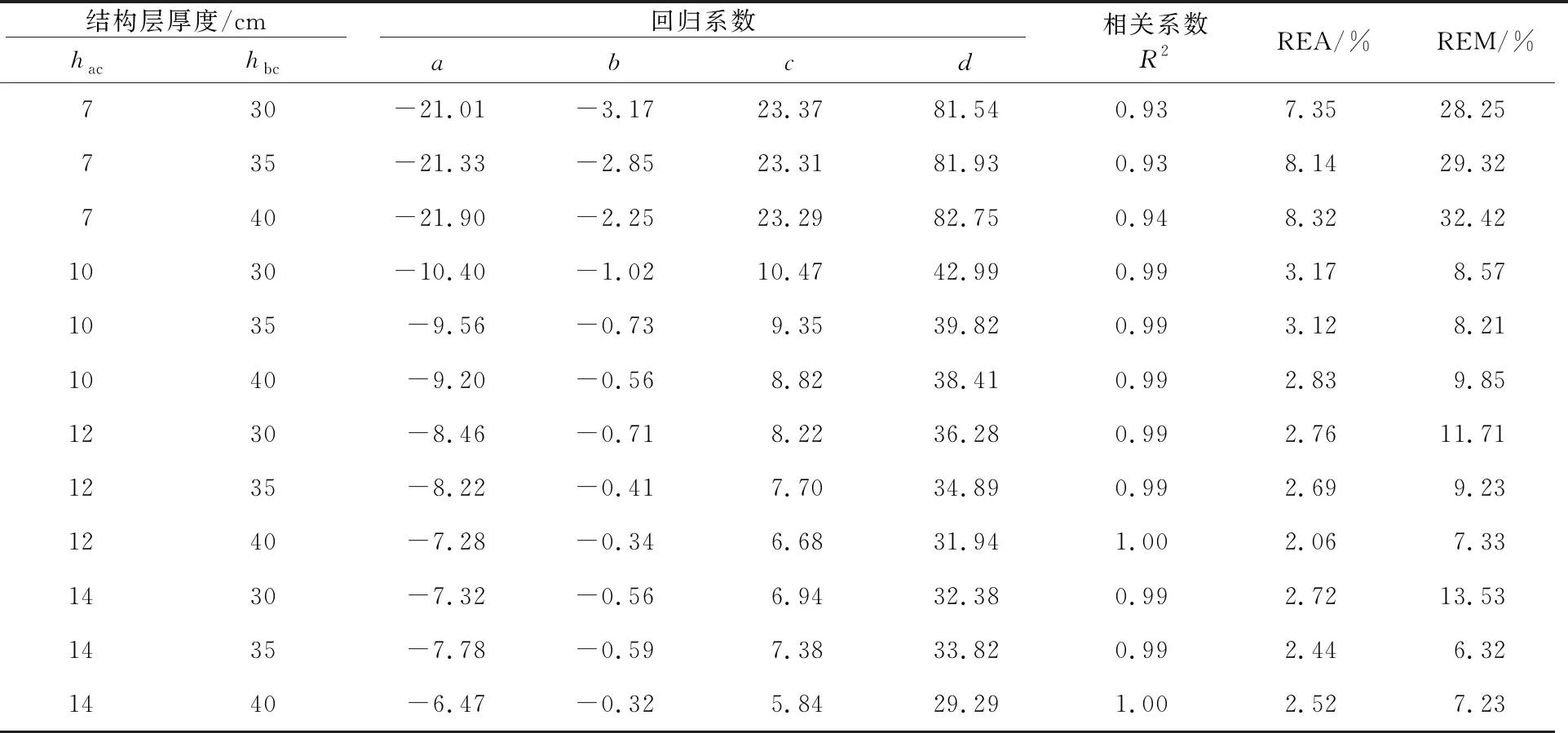
表5 面層模量回歸系數(shù)取值

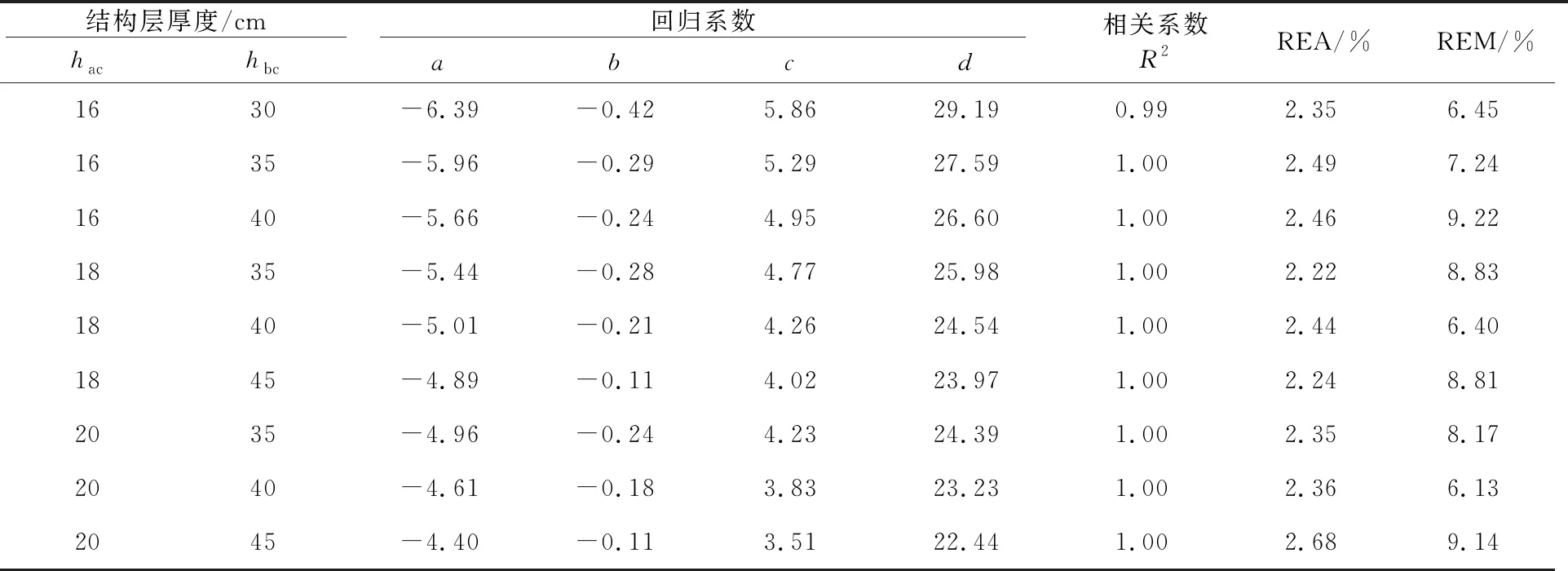
續(xù)表5

由表5可見，在較薄的面層厚度下(面層厚度小于7 cm)，面層模量的計算誤差較大，REA在7.35%～8.32%之間，最大REM為32.42%；而在較厚的面層厚度下，面層模量的計算誤差較小，REA在2.06%～3.17%之間，最大REM為13.53%。May等[12]在利用FWD反演結(jié)構(gòu)層模量時，也發(fā)現(xiàn)了FWD難以準確反演薄瀝青面層模量的問題，并認為這是由于薄瀝青層模量對彎沉值影響較小所致，在反演分析時建議將薄瀝青面層的模量設(shè)定為已知值。因此，本文不建議采用該回歸模型計算薄瀝青面層的模量。

隨后，根據(jù)表5給出的回歸系數(shù)與結(jié)構(gòu)層厚度之間的對應(yīng)關(guān)系，通過逐步回歸分析，進一步建立了回歸系數(shù)與結(jié)構(gòu)層厚度的擬合方程，a、b、c、d計算方法相同，見式(4)。回歸結(jié)果見表6。

a(b,c,d)=k1ln(hac,hbc)+k2hac+k3hbc+k4

(4)

式中：hac、hbc分別為面層厚度、基層厚度,cm；k1、k2、k3、k4為回歸系數(shù)。

同理，建立基層模量與土基模量的反演回歸模型。基層模量的回歸模型見式(5)、(6)，土基模量的回歸模型見式(7)、(8)。

lnEbc=alnCI2+blnS2+cln(AREA6)+d

(5)

a(b,c,d)=k1hbc+k2lnhac+k3lnhbc+k4

(6)

(7)

a(b,c)=k1ln(hac·hbc)+k2hac+k3hbc+k4

(8)

式中：Ebc、Esg分別為基層模量、土基模量，MPa；hac、hbc分別為面層厚度、基層厚度，cm；a、b、c、d、k1、k2、k3、k4為回歸系數(shù)。

模型回歸系數(shù)擬合結(jié)果見表6。

表6 面層模量回歸系數(shù)與結(jié)構(gòu)層厚度對應(yīng)關(guān)系

經(jīng)計算，基層模量的REA在1.01%～2.78%之間，最大REM為14.37%；土基模量的REA在1.39%～2.64%之間，最大REM為13.72%。由此可見，本文所得到的反演回歸模型精度較高，各結(jié)構(gòu)層反演模量的有效范圍基本上能夠滿足工程分析要求。本文提出的反演回歸模型適用于半剛性基層瀝青路面，同時為滿足反演精度要求，瀝青面層適用厚度為10～20 cm，半剛性基層適用厚度為30～45 cm。

4 結(jié)論

1) 彎沉盆參數(shù)敏感性分析表明，對面層模量變化較敏感的彎沉盆參數(shù)依次為：DD2>CI3>S1；對基層模量變化較敏感的彎沉盆參數(shù)依次為：CI2>S2>DD5；對土基模量變化較敏感的彎沉盆參數(shù)依次為：d9>CI8>S7。

2) 利用多元回歸分析方法，提出了考慮層間摩擦接觸的結(jié)構(gòu)層模量反演回歸模型。該模型能夠達到工程精度要求，具有形式簡單，易于工程應(yīng)用的優(yōu)點。但對于面層厚度小于7 cm的情況，不建議采用面層模量回歸模型反演面層模量。