匯管對氣體超聲流量計計量性能的影響

陳文琳，丁 昭，王海同

(1. 新疆維吾爾自治區計量測試研究院，新疆 烏魯木齊 830011; 2. 河北大學質量技術監督學院，河北 保定 071002)

0 引 言

氣體超聲流量檢測技術是近年來流量檢測領域的一個亮點。超聲流量計在計量精度、可靠性、壓力損失、維護費用以及制造成本等方面相比其他計量器具都有獨到的優勢，已有成為氣體流量計量領域最佳選擇的趨勢[1-3]。超聲流量計的準確測量很大程度上依賴于管道內流體的充分發展[4]。理想條件下，進入流量計的氣體流態應是對稱的、充分發展的速度分布狀態，如圖1(a)所示；要準確計量，須避免將流量計安裝在有明顯旋渦或不對稱流動分離等非充分發展湍流的地方[5- 6]（如圖 1(b)所示）。上游管路配置會影響進入流量計的氣體速度廓線，進而影響測量準確度[7- 8]。流量標準裝置中通常采用匯管布置使管道中的流體理想化。但當下游直管段長度不足時，匯管會成為影響流體速度分布的阻流件[9- 10]。

圖1 圓管內流動速度廓線

近年來，人們通過流體實驗、理論分析和計算模擬[11]等方法對如何提高超聲流量計的計量性能進行了大量研究[12-16]。要想消除匯管對下游超聲流量計計量性能的影響，需要從本質上了解匯管對流體流態的擾動情況，掌握匯管下游的速度分布[10]。LIU E B等利用CFD模擬了匯管對超聲流量計的影響，研究了不同匯管直徑、長度對下游管道中的速度分布產生的影響[17]。HALLANGER A等利用CFD對挪威大陸架海上設施的天然氣出口計量站中觀察到的特征進行了分析，結果表明，上游管道的幾何形狀和入口匯管本身的幾何形狀都會影響流體的速度廓線，從而影響測量結果[18]。

鑒于單純的實驗研究周期長、成本高、易受外界條件干擾，且實驗無法準確地給出流場的三維流動信息；而單純的數值模擬方法若沒有實驗的驗證，也無法保證其研究結果的可靠性，本文采用一套高壓音速噴嘴法空氣流量標準裝置研究了匯管對超聲流量計計量性能的影響：分別在安裝流動調整器[19- 20]和無流動調整器兩種條件下進行實驗，比較了兩種條件下的測量結果的差異。結合各個聲道的實驗數據對速度分布進行了分析，對由匯管產生的流態畸變進行了討論。為了進一步可視化地呈現不同安裝條件下管道內的速度分布，將裝置結構簡化為上下游都有匯管的實驗管路，在驗證可靠性的基礎上，利用CFD方法分別對有無安裝流動調整器的不同條件下計量段內（流量計安裝區域）的流場進行模擬，觀察不同入口流速下實驗管道內速度分布，研究匯管對速度分布產生的影響及安裝位置對超聲流量計測量結果的影響。

1 多聲道超聲流量計工作原理

實驗采用內徑為100 mm的雙斷面8聲道超聲流量計。其聲道布置如圖2所示。在1、2兩個斷面內分別平行布置4個聲道，從上到下四個聲道分別為A、B、C、D，各聲道與管道軸線的夾角為60°。聲道位置按照Gauss-Jacobi積分方案進行布置，如表1所示。測量過程中得到每條聲道上的流速后[21-22]再按照相應權重系數加權求和后獲得流量。

圖2 實驗用超聲流量計聲道位置示意圖

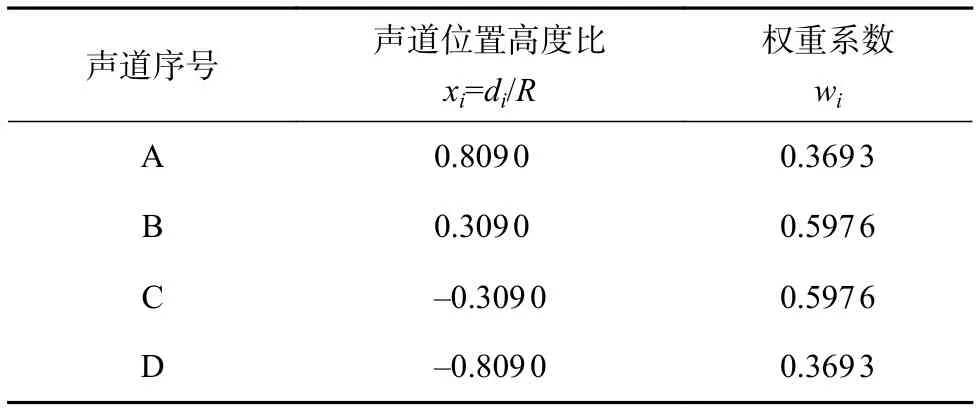
表1 聲道位置及權重系數

對于單個測量斷面的流量Q有：

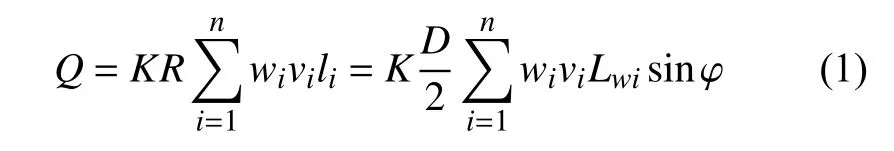
式中：K——修正系數，用于修正由線性平均速度轉換為面平均速度引起的誤差；

D——管道內徑；

wi——聲道i的權重系數；

vi——聲道i測得的線平均速度；

Lwi——聲道長度，即發射探頭到接收探頭之間的距離；

li——聲道長度在截面上的投影；

φ——聲道線與管道軸線的夾角；

n——弦的路徑數。

對于雙斷面測量，取兩個斷面所測體積流量的平均值即為最終的流量值。

2 流動調整器對測量結果的影響

實驗在中國計量科學研究院高壓音速噴嘴法空氣流量標準裝置上完成。該音速噴嘴裝置由16臺音速噴嘴作為標準器，壓力范圍為0.2～2.5 MPa、流量范圍為20～400 m3/h，相對擴展不確定度可達到0.13% (k=2)，裝置結構如圖3所示。

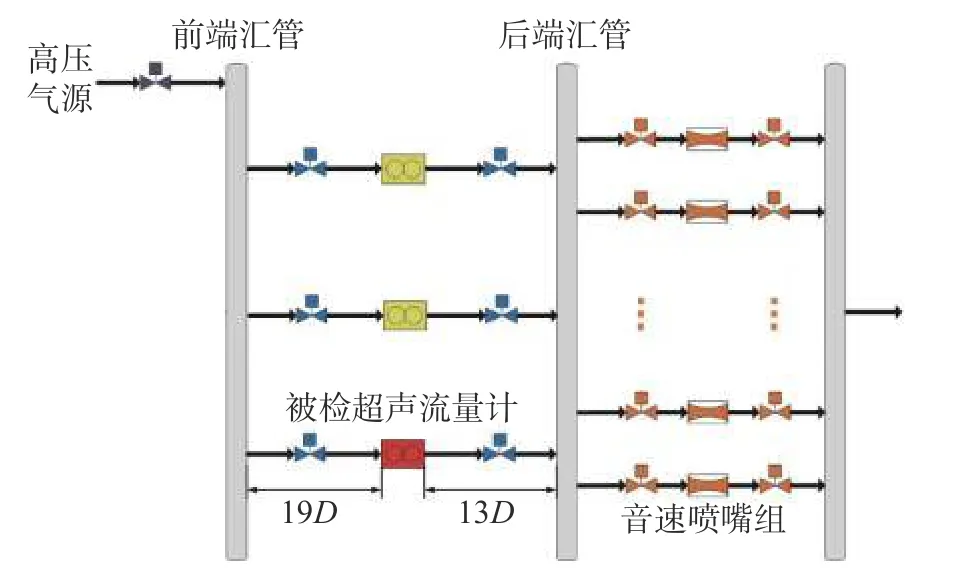
圖3 標準裝置結構示意圖

實驗測量分別在安裝流動調整器和無流動調整器兩種條件下進行，其中流動調整器安裝在流量計上游閥門出口處，距離匯管為7D，距離流量計為12D。兩種條件下的實驗過程中壓力p、溫度T、流量Q都控制在相同范圍內，保證兩次試驗過程中雷諾數Re接近。每次實驗選擇5個流量點，每個流量點測量4次，具體條件及測量結果見表2，測量結果E由流量Q與從標準裝置獲得的標準流量Qref之間的相對示值誤差表示

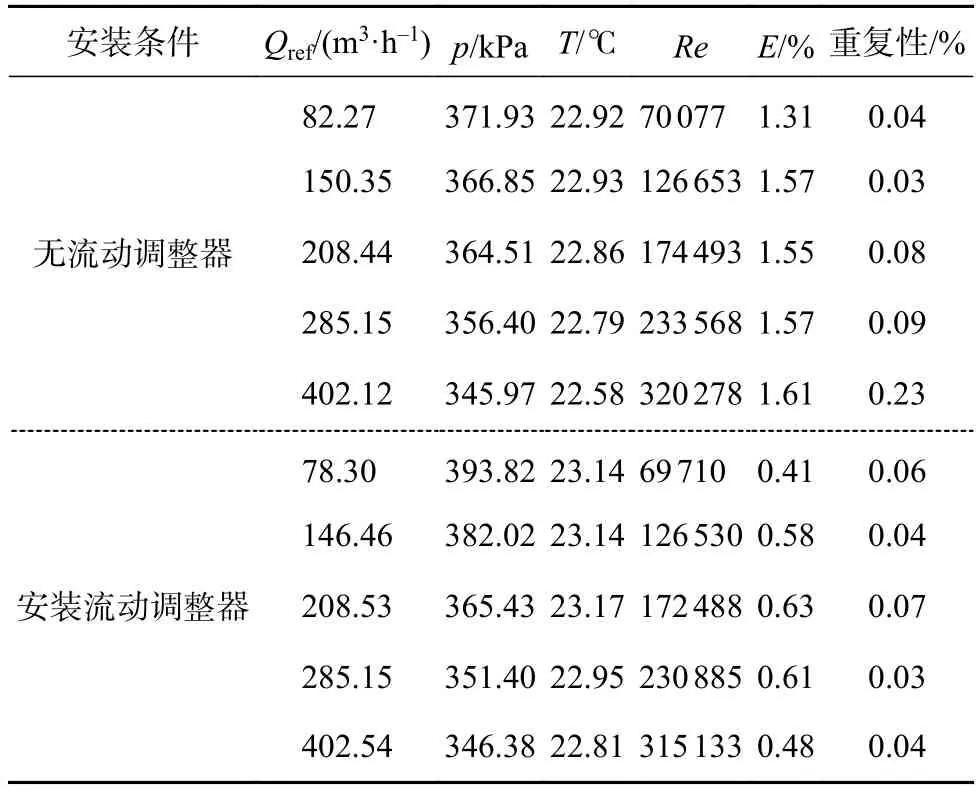
表2 實驗條件及測量結果

表2直觀地呈現了安裝流動調整器前后測量結果的差異：無流動調整器時測量誤差為1.5%左右，而安裝流動調整器后，誤差大幅下降至0.5%左右，安裝流動調整器的測量結果比無流動調整器的減小1%；同時，無流動調整器時的測量結果更為分散，重復性較差。實驗用超聲流量計最大允許誤差為±1%，無流動調整器時的測量結果已超出其所允許的測量誤差范圍，即流場條件不符合流量計的測量要求。

圖4給出了安裝流動調整器前后兩個測量斷面內的速度分布。從圖中可以看出，無流動調整器時，兩個斷面內的流場沒有達到充分發展的狀態，速度分布明顯不同（圖4(a)）；而安裝流動調整器后，兩個斷面內的速度分布都接近于充分發展的狀態（圖4(b)）。

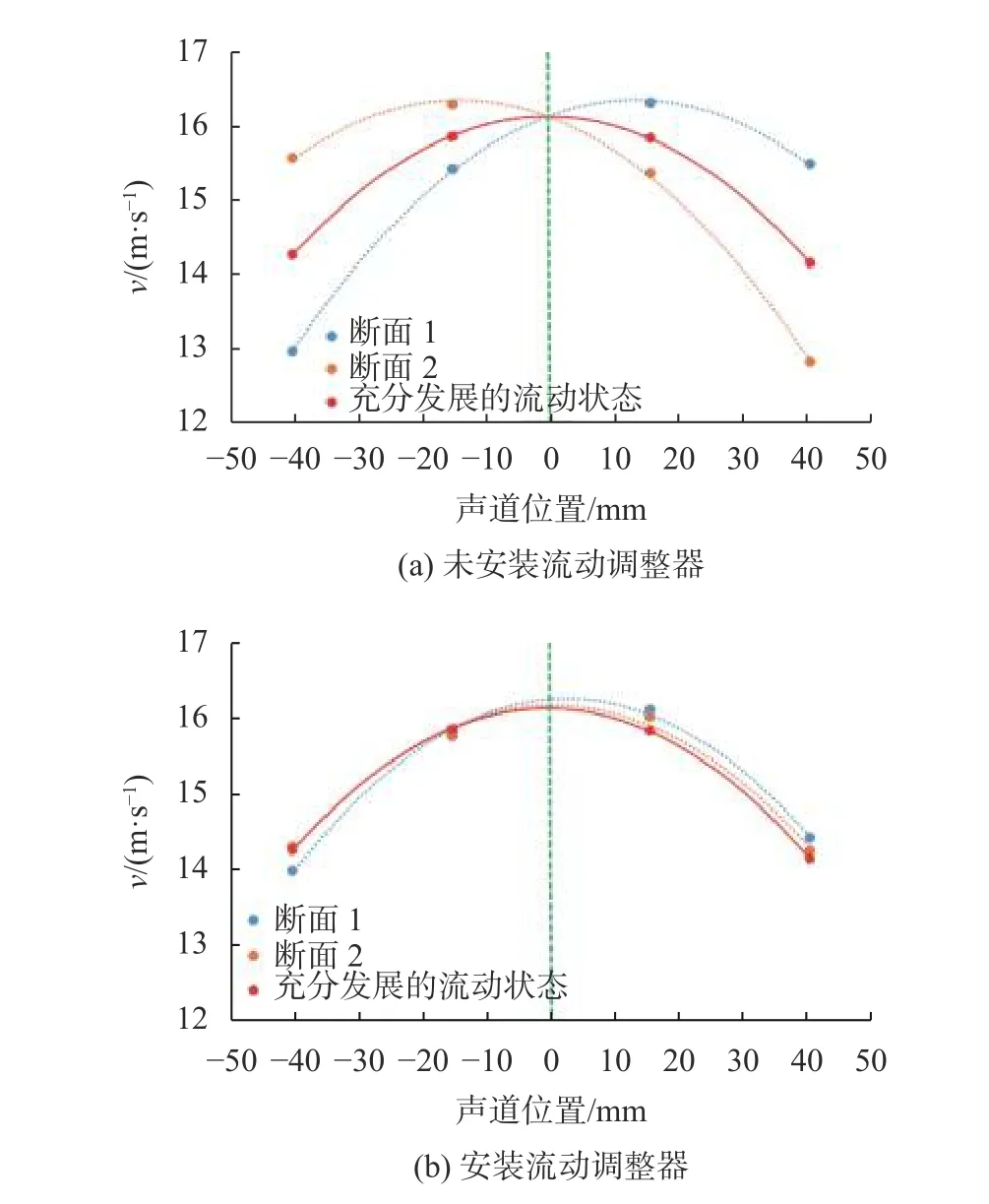
圖4 兩個測量斷面的速度分布（Q=402 m3/h）

實驗過程中超聲流量計上游直管段長度為19D，下游直管段長度為13D（圖3）。實驗過程中上下游球閥均處于全開狀態，可視為直管段，管道兩端為匯管，無其他配置。結合實驗結果可知，無流動調整器時流體從匯管流出后會產生嚴重的流態畸變，導致測量誤差偏高；安裝流動調整器后，流態畸變可被有效消除，從而大幅提高測量準確度。

為了直觀地觀察管道內速度分布，進一步利用CFD對流場進行了模擬。

3 數值仿真方法

3.1 幾何建模和網格劃分

數值模擬所采用物理模型基于音速噴嘴法空氣流量標準裝置，如圖5所示。其中前后匯管直徑均為 200 mm，長度為 2000 mm，前端匯管入口處有90°彎頭，彎頭前取200 mm的直管段；實驗管段（流量計安裝管段）直徑D為 100 mm，長度為 3500 mm即35D；流動調整器為板式流動調整器，結構如圖6所示，安裝在實驗管段進口1D位置處。

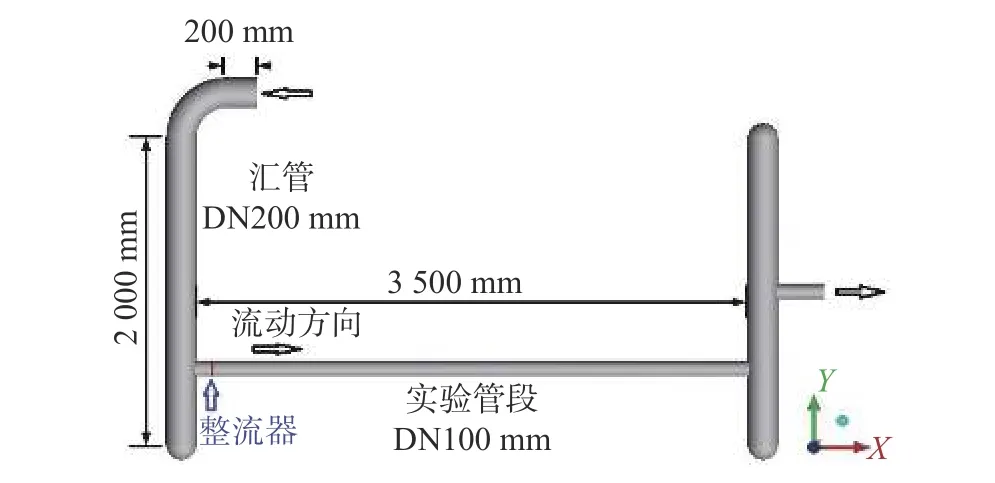
圖5 數值模擬模型示意圖

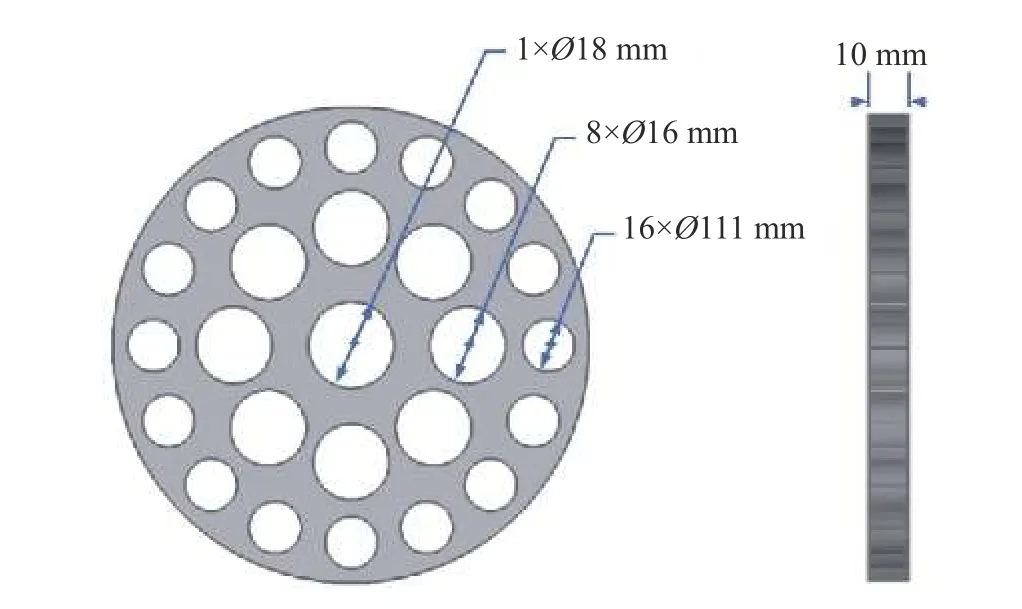
圖6 板式流動調整器示意圖

3.2 控制方程

模擬過程中由于流體速度較低，按照不可壓縮流體處理。對于不可壓縮流體，其湍流控制方程由連續性方程和動量方程組成：

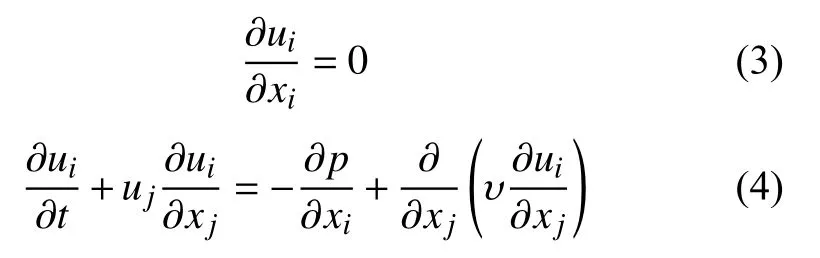
式中：ui(i=1,2,3)——速度在三個不同方向上的分量；

p——流體微元上的壓力；

υ——運動粘度。

3.3 湍流模型選擇及邊界條件定義

利用Fluent進行模擬計算。模擬參數為空氣流量標準裝置的中的實際值。

介質為空氣。壓力：0.36 MPa；溫度：22.8 ℃；密度：4.2 kg/m3；粘度：1.81×10–5kg/(m·s)。

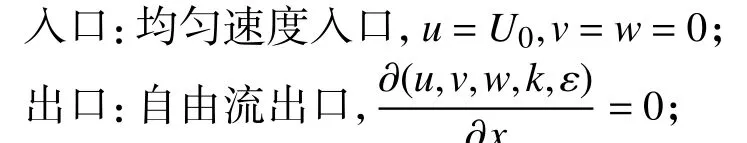
固壁邊界：壁面采用無滑移邊界，u=v=w=0，粗糙度為0.5。

由于參照的空氣流量標準裝置的流量范圍為20～400 m3/h，為研究全量程范圍內實驗管道中的速度分布，仿真計算的入口速度U0分別取0.25 m/s、1.25 m/s、2.5 m/s、3.75 m/s（相應實驗管道內的流速分別為 1 m/s、5 m/s、10 m/s、15 m/s），對應的流量Q分別為 28 m3/h、141 m3/h、283 m3/h、424 m3/h，對應的最小雷諾數為23200，管道中的流體處于湍流狀態，采用 RNGk-ε湍流模型[23]。

3.4 仿真方法可行性驗證

實驗用空氣流量標準裝置的標準器為音速噴嘴，標準流量值由各音速噴嘴組合給出，結合流量標準裝置的實際情況及數值仿真實驗的設計內容，在10 m/s的入口流速條件下，分別對數值仿真結果與安裝流動調整器前后的實驗數據進行了比較。Fluent仿真無法引入聲波傳播時間，因此各聲道上的線平均速度采用對聲道線上各節點速度進行線積分的方法得到。取仿真結果中位于實驗管道19D處的各聲道線平均速度，通過對其進行加權求和得到對應的流量。數值仿真與實驗結果見表3。

表3 數值仿真結果與實驗結果的比較

表中，Qref為實驗過程中標準裝置的流量值，Qsim為通過仿真計算得到的流量值，Esim代表仿真結果與實驗結果之間的相對誤差。由表3可以看出，無論是否安裝流動調整器，仿真結果的誤差均小于4%，因此，可以確定數值仿真計算結果的可靠性。

4 仿真結果分析與討論

對不同入口流速下管道內的流場進行研究，討論不同位置處的速度分布，以及速度分布對超聲流量計測量結果的影響。

4.1 無流動調整器管道中的流場速度分布

圖7給出了入口流速為15 m/s時水平剖面（XY平面）和從下游視角觀察到的不同位置處的軸向剖面（YZ平面）內的速度云圖。圖中展示了流態從畸變恢復至充分發展的整個過程：氣體從前端匯管進入實驗管段時，速度剖面發生畸變，出現明顯的不對稱流動，這種畸變隨著直管段長度的增加逐漸變弱，在25D左右恢復充分發展的狀態。

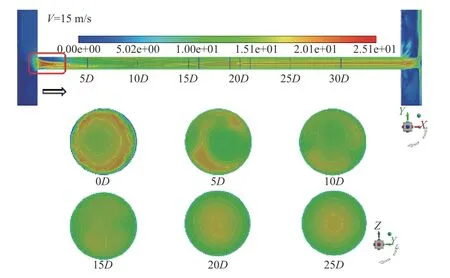
圖7 無流動調整器管道中水平剖面和不同位置處軸向剖面內的速度分布

圖8為下游視角的軸向速度矢量圖。從圖中可以看出，在5D至20D處的剖面中，存在明顯旋渦。隨著直管段長度的增加，旋渦開始消散，個數變少同時強度變弱，至25D處時管道內部的旋渦已基本消散。

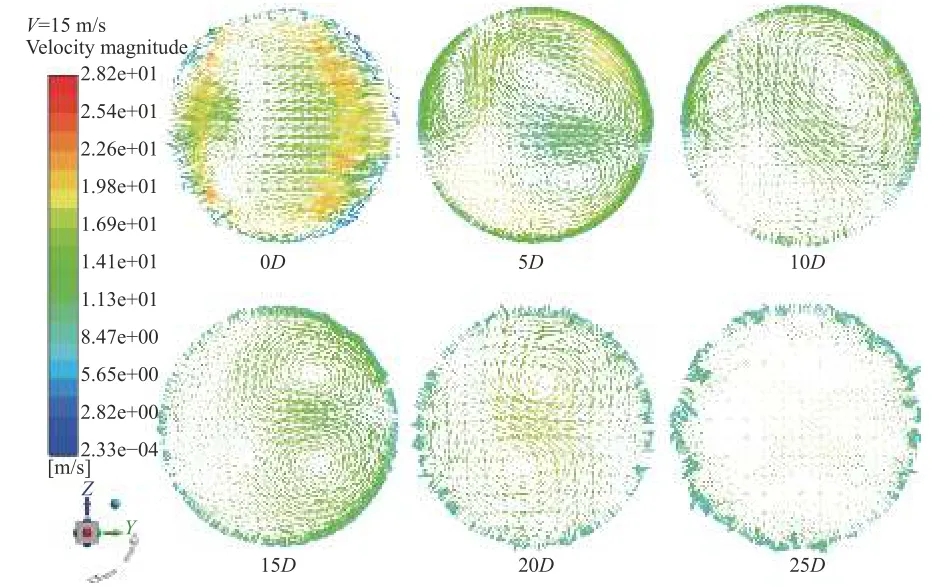
圖8 無流動調整器管道中不同位置處軸向截面速度矢量圖

圖9展示了不同入口速度下的水平剖面內速度分布云圖。從圖中可以看出，速度越大，流態畸變越顯著，相應地所需恢復均勻速度分布的直管段長度也越長；下游直管段長度達到25D后，4種不同流速下的管道內流場均能恢復充分發展的狀態。

圖9 無流動調整器管道中不同入口速度下的水平剖面內速度分布云圖

對最大流速15 m/s時管道內的流場特征進行深入分析。圖10給出了無流動調整器管道中不同位置處的速度廓線，圖10(a)和圖10(b)分別為水平徑向和豎直徑向的速度廓線。從圖中可以看出，與25D處充分發展流場的速度廓線相比，軸向截面5D、10D、15D處的速度廓線有十分明顯的區別，到25D以后的速度廓線基本趨于一致。需要注意的是，同一位置處水平徑向和豎直徑向上的速度廓線并不完全相同，這充分說明管道內的流動為三維湍流。

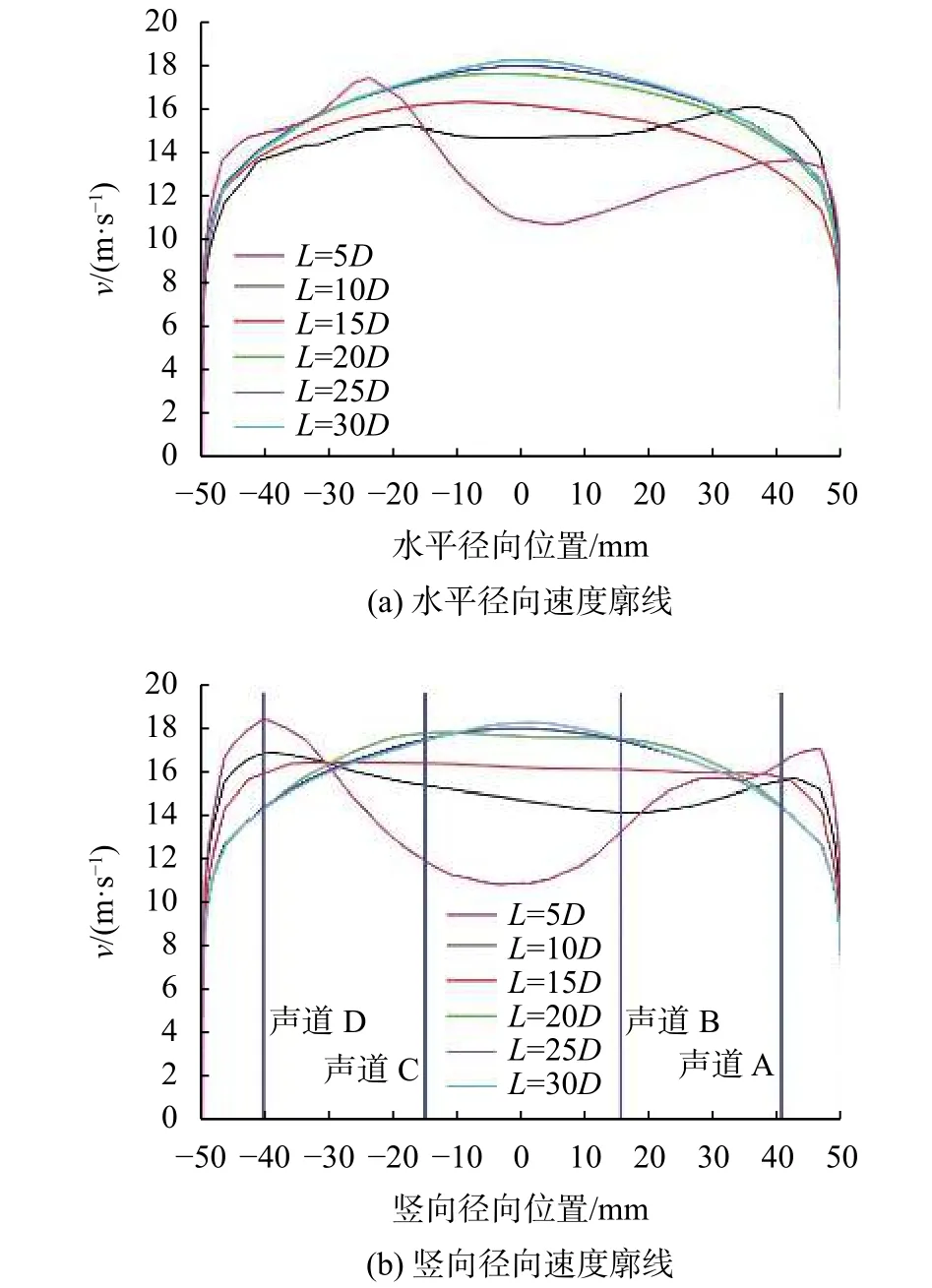
圖10 無流動調整器管道中軸向截面的速度廓線

4.2 安裝流動調整器管道中的流場速度分布

圖11展示了安裝流動調整器后不同入口速度下的速度云圖。從圖中可以看出流動調整器對流場的調整作用很明顯，流體從匯管出來后經過流動調整器的調整，可以在較短直管段長度內恢復充分發展的狀態。

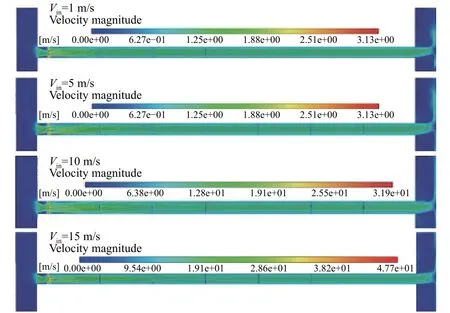
圖11 安裝流動調整器后不同入口速度下的水平剖面內速度分布云圖

與圖8未安裝流動調整器時的速度矢量圖相比，圖12的速度矢量圖顯示流體從流動調整器出來后，5D處管道軸向截面內存在少量較小的旋渦，至15D處旋渦已基本消散，說明流動調整器對消除由匯管帶來的流態畸變非常有效。

圖12 安裝流動調整器后不同位置處的軸向截面速度矢量圖

圖13展示了安裝流動調整器后不同位置處的速度廓線。從圖中可以看出由于流動調整器的存在，流體流過流動調整器時有效流通面積減小，導致流速大幅增加，5D處的速度廓線明顯較高，表明流動調整器的存在使得流體以高速向管道軸心處集中，從而加快了速度分布迅速恢復至充分發展的狀態。10D左右處的速度廓線較未安裝流動調整器時已大幅提高，接近充分發展的狀態。

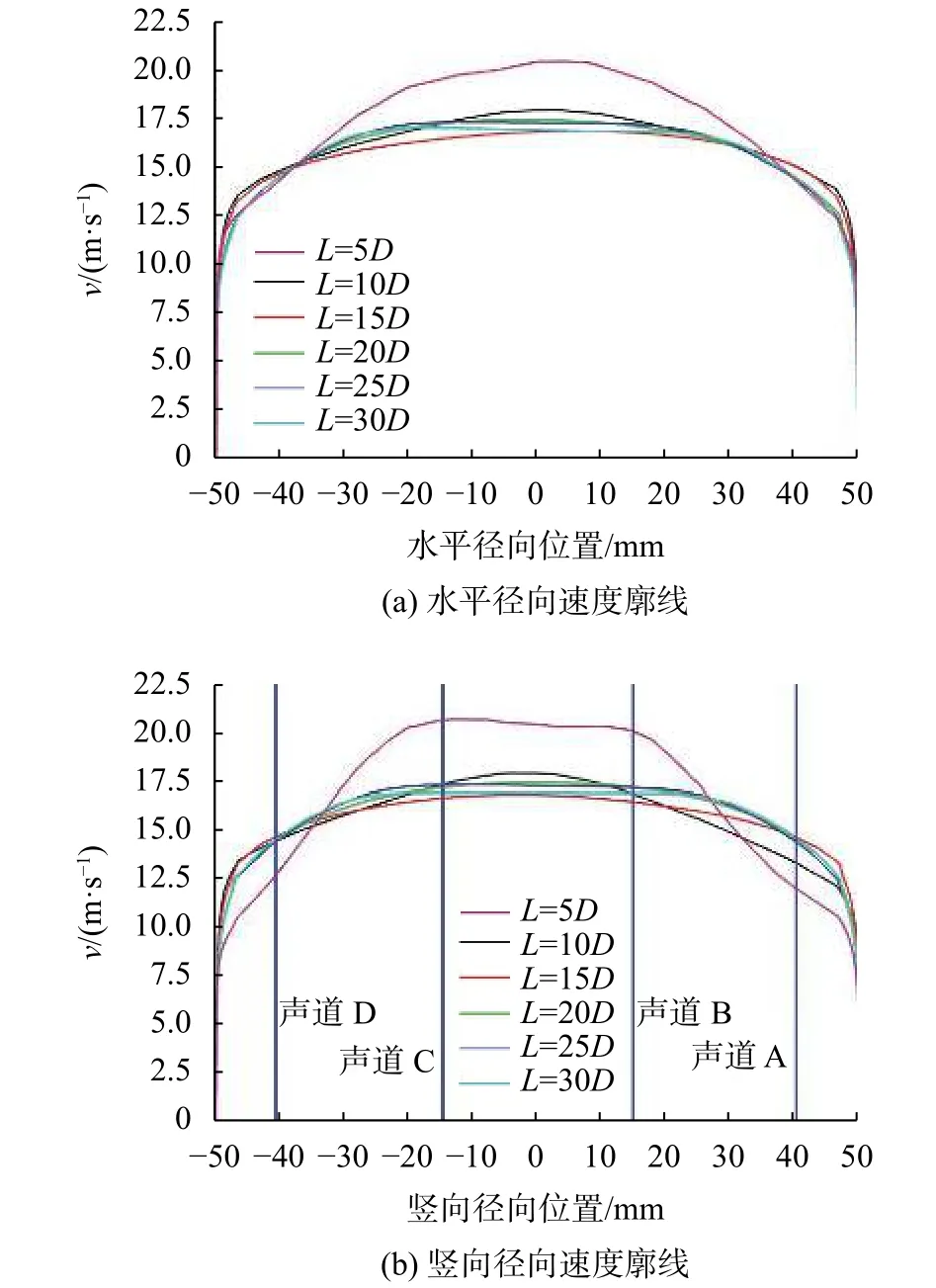
圖13 安裝流動調整器后軸向截面的速度廓線

4.3 不同位置處超聲流量計測量結果

分析不同截面上的速度分布后，分別在5D、10D、15D、20D、25D、30D處取聲道線（如圖14所示），模擬不同位置處的流量。用3.4節的方法，仿真計算得到流量Qsim，將其與仿真過程中的入口流量Qin進行比較，獲得測量誤差Ec：

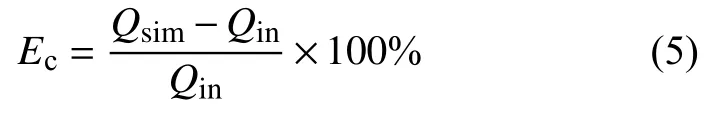
圖14 仿真過程中采用的聲道線示意圖

圖15展示了通過仿真計算得到的流量誤差。結果顯示不論是否安裝流動調整器，流量誤差都隨著上游直管段長度的增加而減小。同一位置處，入口速度越大，誤差越大。在20D到25D之間的結果誤差最小。

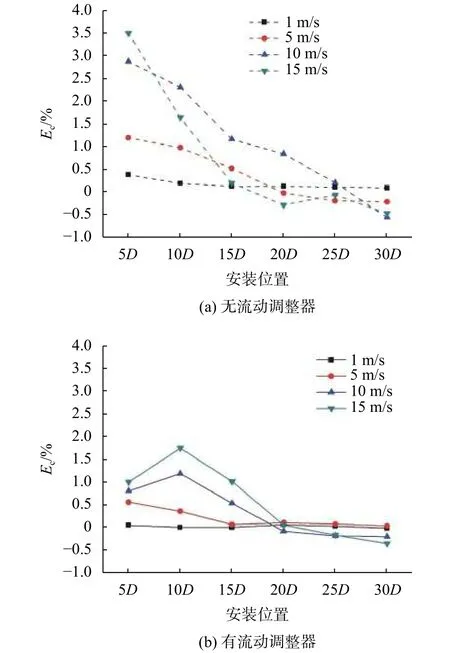
圖15 不同入口速度下不同位置處的測量誤差

仿真結果可以非常直觀地展示出匯管下游管道內的速度分布。但實際實驗管路更為復雜，且此次仿真過程中，簡化的管道模型沒有考慮超聲流量計探頭凸出效應[24]的影響，使得仿真計算結果與實驗結果存在一定差異。下一步工作中，會將仿真模型進一步細化，提高仿真結果的準確性。

5 結束語

通過在高壓音速噴嘴法空氣流量標準裝置上進行實驗，發現無流動調整器時超聲流量計的測量結果約為1.5%，而安裝流動調整器后測量結果約為0.5%。超聲流量計在不同安裝條件下測量結果相差1%，且無流動調整器時測量結果更為分散，重復性較差。造成這一差異的原因是在無流動調整器時裝置前端的匯管導致管道中流態發生畸變。

在實驗結果的基礎上，進一步利用CFD仿真研究了不同安裝條件下的速度分布。結果表明，無流動調整器時，匯管會導致下游實驗管段內流態發生畸變，使速度分布不對稱，流體流動過程中存在明顯的旋渦。即流速越大，畸變越嚴重。而這種畸變隨著直管段長度的增加逐漸減弱，在25D左右恢復充分發展狀態。流動調整器對流場的調整作用很明顯，至15D處旋渦已基本消散，說明流動調整器對消除由匯管帶來的流態畸變非常有效，這在一定程度上提高了超聲流量計測量結果的準確度。本文的研究結果可以為氣體超聲流量計的安裝和使用提供參考。