滬蘇通大橋風-車-橋耦合系統非線性動力響應研究

徐 曼，曾 濱，喬 宏，許 慶，郭薇薇，夏 禾

(1. 中冶建筑研究總院有限公司研究院，北京 100088；2. 北京建筑大學土木與交通工程學院，北京 100044；3. 北京交通大學土木建筑工程學院，北京 100044)

公鐵兩用斜拉橋能合理利用空間、節省建設費用[1]。隨著我國高速鐵路的快速發展，越來越多的大跨度高鐵橋梁選用斜拉橋的設計方案。大跨度斜拉橋通常建設于跨江、海、峽谷等地形區域，風場環境復雜。并且，隨著跨徑的增大，橋梁剛度逐漸降低，對風和列車荷載的敏感性逐漸增加，在拉索垂度效應、結構大變形等幾何非線性因素影響下，動力荷載下的橋梁響應通常呈現出中小跨度橋梁所沒有的非線性特性[2]。國內外學者對風-車-橋耦合振動問題進行了大量研究[3-13]，關注了橫風作用下車-橋系統響應[3,5]，大跨度橋梁氣動特性[3-7]，考慮幾何非線性因素的橋梁非線性響應及結構安全分析[12-14]等。

由于大跨度斜拉橋結構形式的獨特性和風場環境的復雜性，每一座大跨度橋梁的安全運行均需遵循嚴謹細致的研究分析。為了保證橋梁結構自身的服役性能及橋上運行列車的安全性與平穩性，研究復雜風場環境和高速列車荷載下的大跨度斜拉橋非線性響應十分必要。

滬蘇通公鐵兩用長江大橋(以下簡稱滬蘇通大橋)是世界首座跨度突破1 km 的公鐵兩用型斜拉橋，該橋地處長江中下游，受海洋性季風影響，風場條件復雜，車輛運行時直接暴露于自然風場，風對橋梁及行駛車輛的作用顯著。劉德軍等[15]和張騫等[16]以滬通長江大橋為研究背景，進行了不同風速激勵下列車以不同速度通過橋梁時系統的動力響應分析。然而，上述分析中未考慮橋址區實際風場作用特點，且忽略風荷載非線性對車-橋耦合系統響應的影響。

因此，本文以滬蘇通大橋為工程背景，基于實測風場數據，考慮幾何非線性因素影響，進行滬蘇通大橋的風-車-橋耦合振動分析，對保證大橋在自然風場中的結構安全以及行車安全性、舒適性，具有重要的研究價值和工程意義。

1 工程概況

滬蘇通大橋全長2296 m，主跨跨徑1092 m，為雙塔三索面斜拉橋，具體橋跨布置如圖1 所示。上層橋面為6 車道高速公路；下層為4 線鐵路，分別為2 線通蘇嘉城際鐵路(設計速度250 km/h)和2 線滬通鐵路(設計速度200 km/h)。

圖1 滬蘇通大橋立面布置圖 /mFig. 1 Elevation of Hu-Su-Tong Yangtze River Bridge

大橋采用鋼桁架主梁，橫斷面如圖2 所示。主梁鋼桁架弦桿采用帶肋空心矩形截面，由500 MPa級高強鋼板制造，共164 個節間；主塔及橋墩采用C60 混凝土；斜拉索鋼絞線采用2000 MPa 級高強度平行鋼絲。

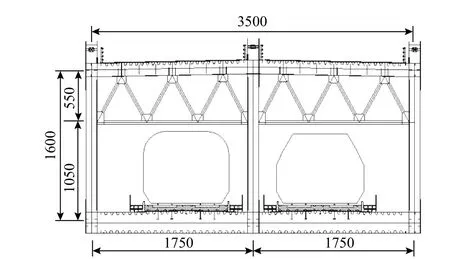
圖2 滬蘇通大橋主梁橫斷面 /mmFig. 2 Cross section of girder of Hu-Su-Tong Yangtze River Bridge

2 風-車-橋耦合系統建立

2.1 風荷載模型

滬蘇通大橋地處長江中下游，臨近入海口，受海洋季風氣候影響大，風場環境復雜，規范給出的設計風速無法準確描述橋位處的風場特征。筆者開展了實地風場測試[17]，提取風場特征，經比較，規范風譜與實測風譜數據差異明顯，采用實測譜參數模擬的風速時程與實際風場特征吻合度高。

基于滬蘇通大橋節段模型風洞試驗[18]獲得的三分力系數，結合基于實測的功率譜參數模擬主梁橫/豎橋向、主塔橫橋向等多組一維脈動風速場，以14 m 為主梁模擬點間隔，考慮上、下橋延伸距離，建立全橋風荷載模型。在此基礎上，對車輛運行位置處線性插值計算得到車輛風荷載。表1 給出了瞬時風速30 m/s 時主梁跨中抖振風荷載極值。

表1 瞬時風速30 m/s 時滬蘇通大橋主梁跨中抖振風極值Table 1 Max buffeting wind load at mid-span with U=30 m/s

2.2 橋梁模型

本文采用ANSYS 建立滬蘇通大橋全橋有限元模型，采用Ernst 公式[18]修正拉索彈性模量以表征垂度效應。

提取主梁的前5 階振型及自振頻率如表2 所示，將其與文獻[18]給出的滬蘇通大橋有限元模型的自振特性比較。可以看出，除縱飄振型外，本文橋梁模型的前5 階振型與文獻一致，且自振頻率的差異率在±5%以內，縱飄是大跨度橋梁的常見低頻振型，符合客觀規律，可認為本文模型有效。

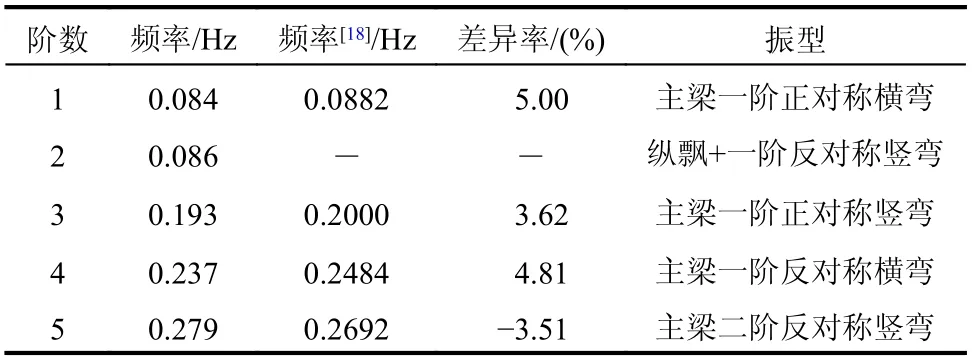
表2 滬蘇通大橋自振頻率及振型特點Table 2 Natural frequencies and mode-shape characteristics

2.3 非線性因素

由于風-車-橋耦合分析中，橋梁結構一般仍處于彈性狀態，因此本文僅考慮幾何非線性因素的影響。考慮梁柱效應與大位移效應的影響，建立橋梁結構的非線性運動方程：

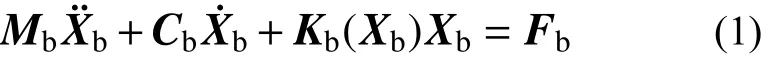
式中：M、C和K分別為質量矩陣、阻尼矩陣和剛度矩陣；下標b 代表橋梁；剛度矩陣Kb與橋梁的位移向量Xb相關，并由結構自身的彈性剛度矩陣KE和隨位移變化而改變的幾何剛度矩陣KG組成：

由式(2)可知，為了考慮幾何非線性的影響，需在每一計算時間步之后重新計算橋梁的內力和位移，以更新剛度矩陣進行下一時間步的計算。

自然風場中，橋梁各位置響應各異，結構變形導致風攻角變化而影響風荷載分布，進而改變橋梁位移響應，體現出風荷載的空間非線性特征[19]。

2.4 風-車-橋耦合模型

以16 節車輛編組((3 動+1 拖)×4)的CRH2 高速列車為研究對象，基于剛體動力學假定建立車輛模型。車輛模型與橋梁模型之間的相互作用通過輪軌關系實現，計算時假定橫向蠕滑、垂向密貼。將風以外荷載的形式作用于車-橋耦合系統，軌道不平順則采用德國低干擾譜模擬獲得。最終建立風-車-橋耦合系統的運動方程為：

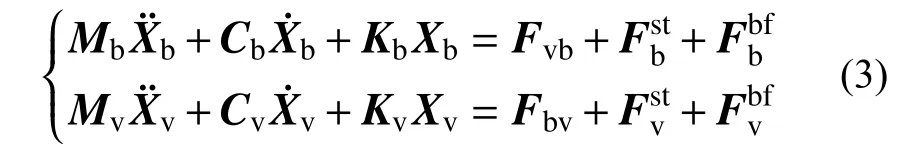
式中：下標v 為車輛；Fvb和Fbv分別為車輛與橋梁系統間的相互作用力；上標st、bf 分別為靜風荷載和抖振風荷載。

采用全過程迭代法[20]對耦合系統的動力響應進行求解，求解過程中考慮橋梁結構非線性的影響。考慮到受荷載作用的最不利情況，在以下分析中，橋梁動力響應取自直接承受列車荷載作用的鐵路橋面節點。

3 風-車-橋系統非線性動力響應分析

設定瞬時風速30 m/s，車速200 km/h 為基本工況，多種非線性工況風-車-橋耦合系統動力響應結果如下。

3.1 耦合系統分析模型的驗證

為驗證耦合動力分析結果的有效性，本節以豎向加速度響應為例，繪制了主梁多位置處的豎向加速度時程曲線和低頻區頻譜曲線如圖3 所示。

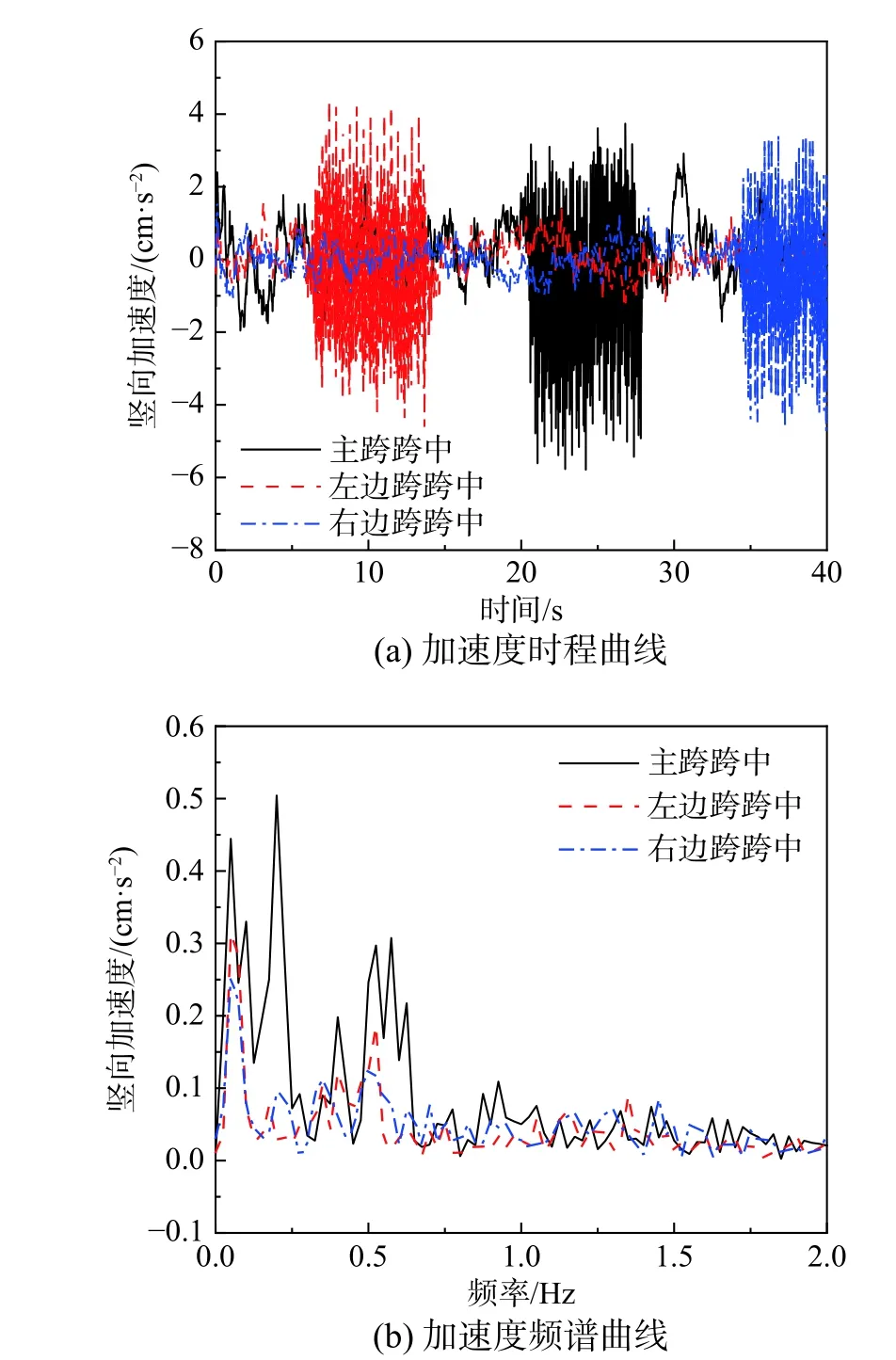
圖3 主梁豎向加速度時程及頻譜曲線Fig. 3 Bridge vertical acceleration and spectrums

根據圖3(a)，豎向加速度呈現出明顯的受激振動特征，列車行駛過程，主梁自左向右呈現出典型的此起彼伏振動趨勢，符合客觀規律。根據圖3(b)，可識別0.2 Hz 和0.4 Hz 的自振頻率，分別與主梁一階正對稱豎彎(0.193 Hz)和主梁二階正對稱豎彎(0.400 Hz)吻合，認為耦合系統分析結果與橋梁模型的特征吻合。

3.2 非線性因素對橋梁動力響應的影響

以不考慮非線性因素的工況為基本對照，分析非線性因素對風-車-橋耦合系統橋梁動力響應的影響程度，得到的橋梁動力響應最大值如表3。圖4 給出了主梁跨中豎向加速度時程曲線對比，圖5 給出了考慮非線性因素下橋梁各動力響應相對差。

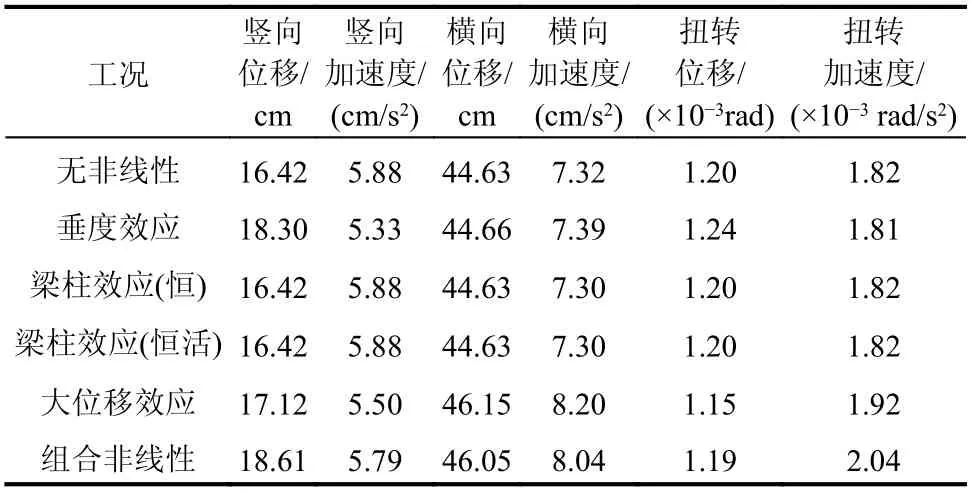
表3 不同非線性因素下橋梁動力響應最大值Table 3 Bridge maximum dynamic responses under nonlinear factors

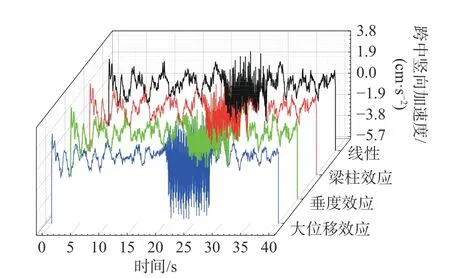
圖4 多工況橋梁跨中豎向加速度時程曲線Fig. 4 Vertical acceleration histories of bridge on mid-span in different cases

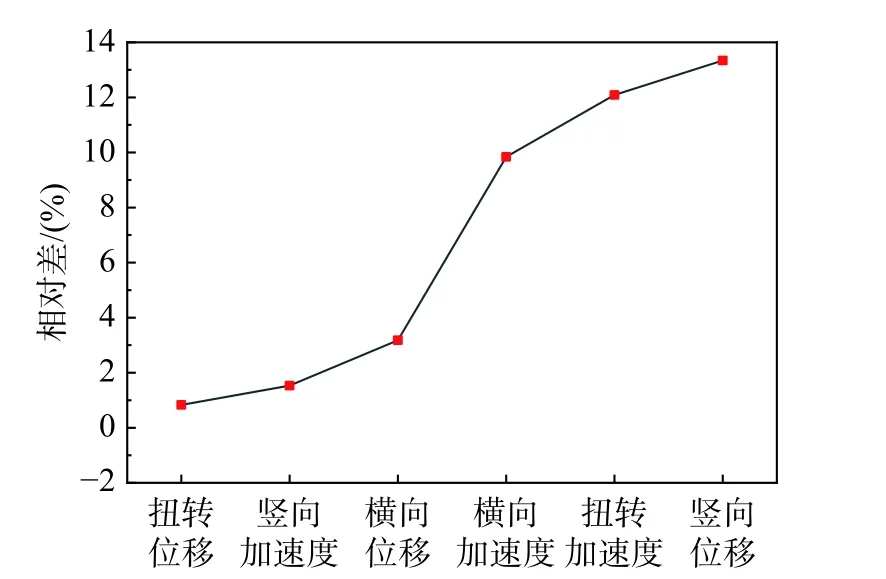
圖5 考慮組合非線性因素的橋梁響應相對差Fig. 5 Relative error of bridge responses between linear and nonlinear conditions

由表3 可知，非線性因素對橋梁動力響應影響較大，其中大位移效應影響最大，垂度效應對豎向動力響應的影響較大。梁柱效應的影響較小，且計入活載內力前后，梁柱效應影響差異小。根據圖4，除幅值變化外，非線性工況下主梁響應的波動強度更明顯。根據圖5，綜合非線性因素后，豎向位移、扭轉加速度、橫向位移受影響程度最大，達到10%以上。

3.3 非線性因素對車輛動力響應的影響

圖6 給出非線性/線性工況橋上列車動力響應最大值相對差曲線，圖7 給出了某節車體在多工況下的橫向加速度曲線。

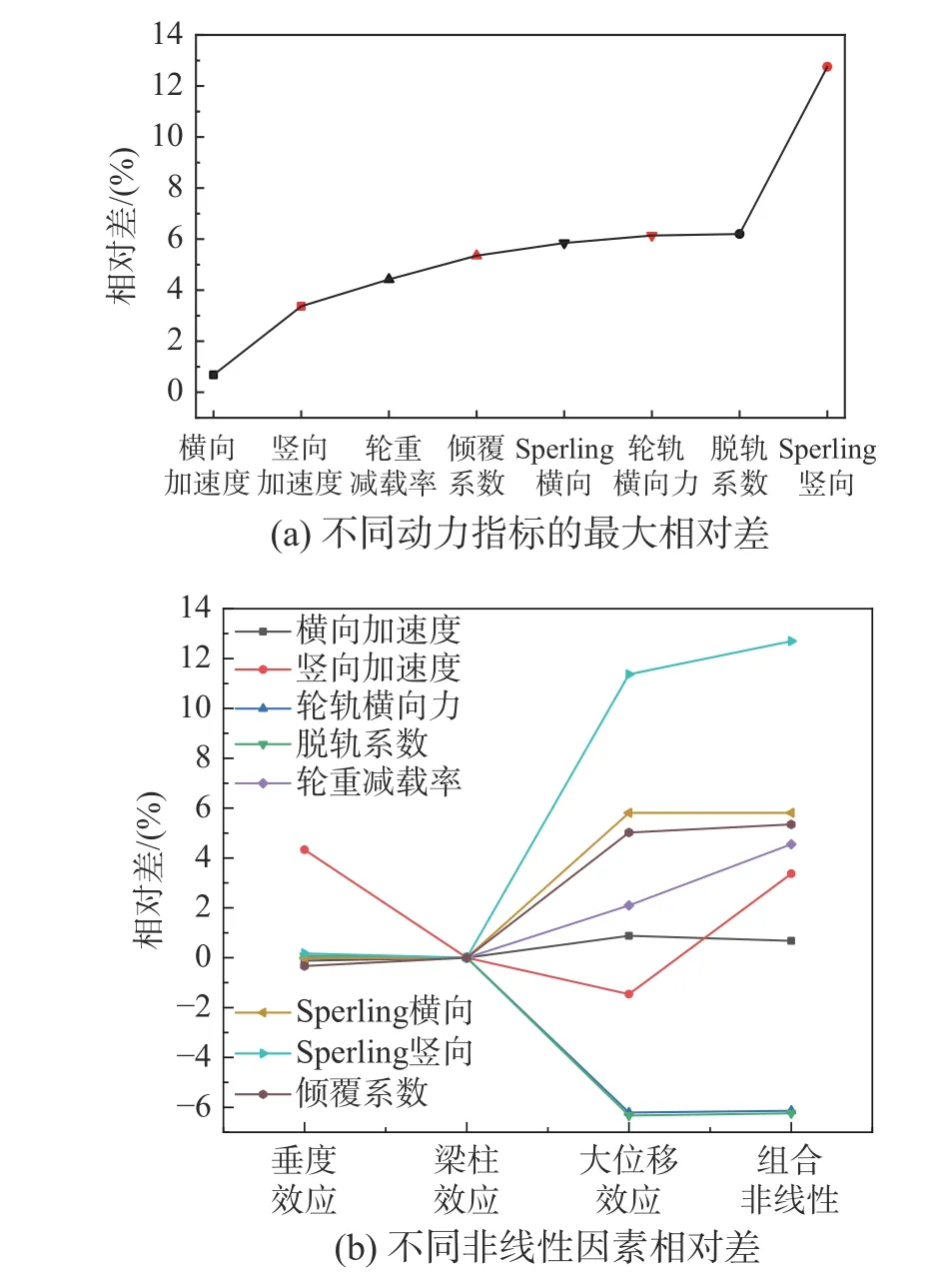
圖6 非線性與線性工況的列車響應相對差Fig. 6 Relative error of train responses between linear and nonlinear cases

由圖6(a)可知，非線性因素對車輛的多項動力指標有影響，其中，Sperling 豎向受影響最大，達到12.75%，除橫向加速度外，其余動力指標影響程度均在5%左右。結合圖6(b)和圖7，大位移效應導致車輛動力響應峰值增大，且顯著增大低頻成分，垂度效應對車輛豎向動力指標的影響較為顯著，梁柱效應對車輛動力響應的影響很小。

圖7 多工況下車體橫向加速度時程曲線Fig. 7 Horizontal acceleration histories of train in different cases

3.4 考慮非線性因素的行車安全性分析

基于上述分析，采用考慮非線性因素的風-車-橋耦合模型進行多工況下的車-橋響應分析，得到車速200 km/h，瞬時風速從0 km/h～40 m/s 時的9 組工況下車輛最大動力響應，和瞬時風速30 m/s，車速160 km/h～250 km/h 的5 組工況下車輛最大動力響應如表4 所示。圖8 給出了不同車速和不同風速工況下的車輛輪重減載率最大響應曲線。

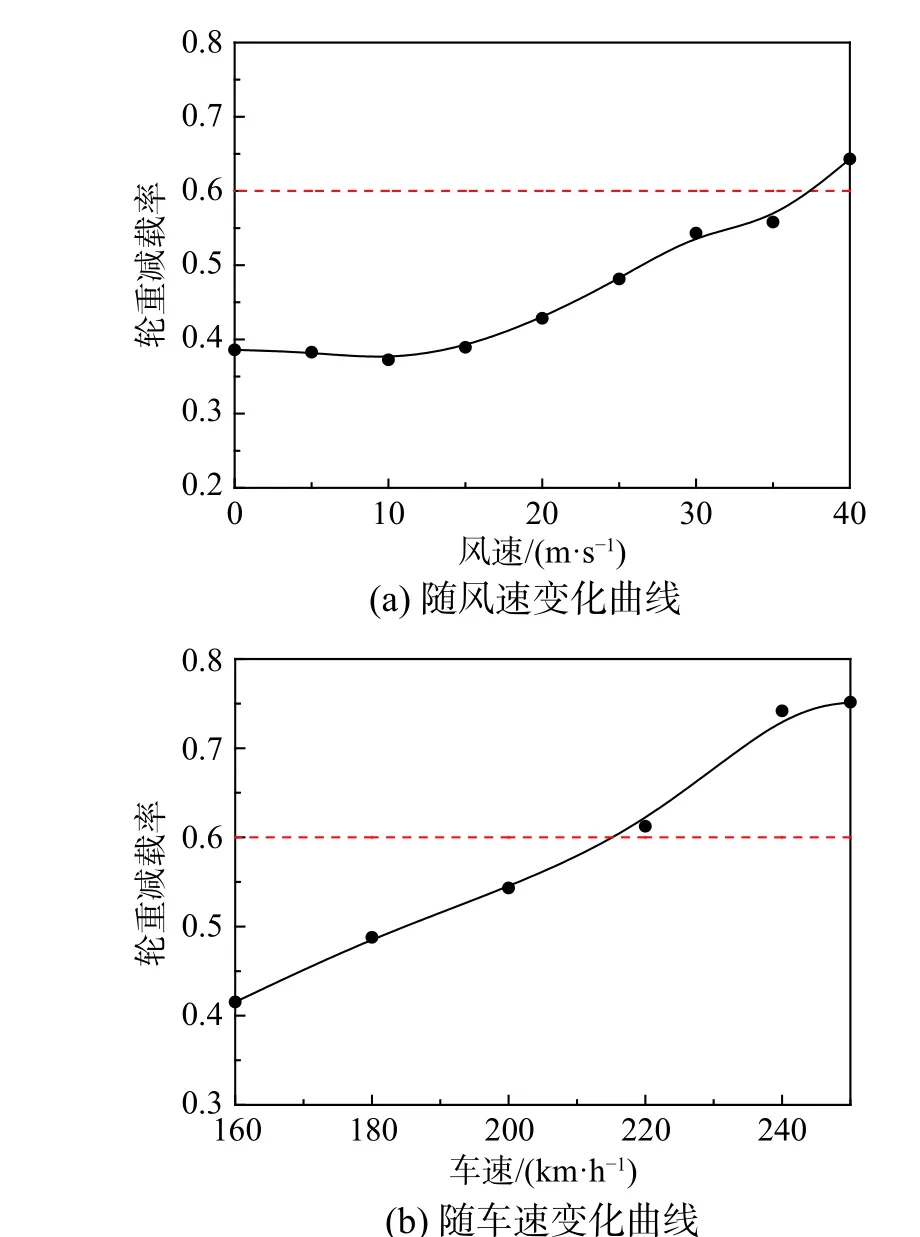
圖8 車輛輪重減載率最大值隨風速/車速的變化曲線Fig. 8 Maximum wheel off-load index of train vs. wind/train speeds

表4 不同風速/車速下車輛動力響應最大值Table 4 Maximum dynamic responses of train under various wind/train speeds

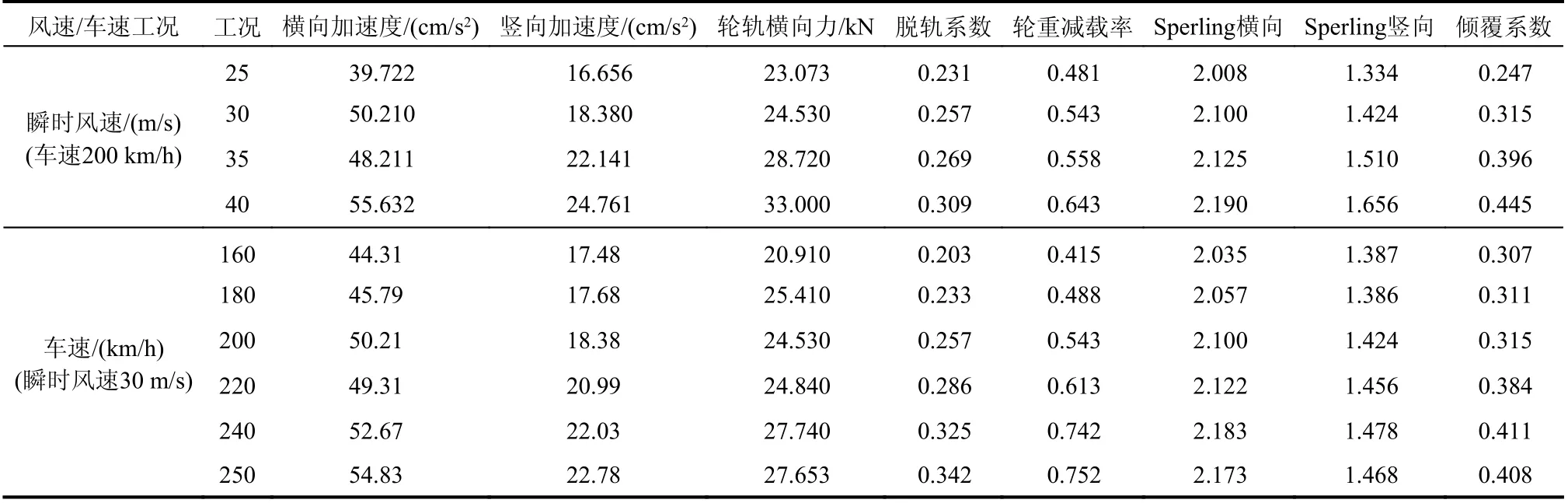
續表4

根據《鐵道車輛動力學性能評定和試驗鑒定規范》[21]和鐵道部《鐵道機車動力學性能試驗鑒定方法及評定標準》[22]，輪重減載率應小于0.6(圖8 中虛線)。

由表4 及圖8 可知，當車速為200 km/h，瞬時風速超過35 m/s，或當瞬時風速為30 m/s，車速超過210 km/h 時，車輛輪重減載率指標超出安全閾值，車輛的安全性能受到威脅。

4 結論

本文以滬蘇通大橋為工程背景，考慮大跨度斜拉橋在自然風場中的幾何非線性特征，基于實測風場特征模擬風荷載，建立風-車-橋耦合系統動力模型，通過多工況計算，分析了非線性因素對橋梁與車輛動力響應的影響，并給出滬蘇通大橋行車安全性分析，主要結論如下：

(1)根據橋梁模型自振特性和動力響應頻譜分析，本文的橋梁模型及考慮幾何非線性因素的風-車-橋耦合系統動力分析結果，符合客觀規律并與既有研究結果吻合。

(2)幾何非線性因素對風-車-橋耦合系統振動的影響不可忽略，考慮非線性因素時，橋梁和車輛的多個動力響應指標均有一定程度的增大，忽略非線性因素可能導致結構動力響應分析和行車安全性分析偏不安全。

(3)非線性因素中，大位移效應對橋梁和車輛的動力影響最顯著，垂度效應對豎向動力響應影響較大，梁柱效應的影響較小。

(4)對于滬蘇通大橋，當車速為200 km/h，瞬時風速超過35 m/s，或當瞬時風速為30 m/s，車速超過210 km/h 時，車輛輪重減載率指標超出安全閾值，車輛的安全性能受到威脅。

本文的研究成果表明，對于大跨度斜拉橋，幾何非線性因素對橋梁結構及橋上列車運行的安全性具有重要的影響，是分析中不可忽視的重要因素。本文對滬蘇通大橋開展的多種工況自然風場-車輛-橋梁耦合振動分析，為世界首座跨度超1 km 的公鐵兩用斜拉橋的安全運營提供了可靠的研究支撐。而滬蘇通大橋其復雜的風場環境、大跨度帶來的結構非線性，汽車荷載與風-列車-橋梁的耦合作用以及多線行車的荷載工況等多方面的耦合影響，仍有待更豐富的科學研究補充探明。