基于云模型和多目標規劃的FADS系統測量精度的研究

胡嘉悅, 賈乾磊, 章衛國, 李廣文, 史靜平, 劉小雄

(西北工業大學 自動化學院, 陜西 西安 710072)

2018年和2019年,印度尼西亞獅航和埃塞俄比亞航空公司先后發生兩起重大空難事件,共計造成346人死亡。事后經過多方調查,一個重要原因是波音737MAX型客機在飛行過程中迎角傳感器的測量結果出現異常,進而影響了飛行控制系統,最終導致飛機墜毀。因此,保證大氣數據傳感器測量精度是至關重要的,將直接關乎到整個飛行安全。

傳統的探針式大氣數據傳感器以空速管為基礎,配合迎角傳感器、側滑角傳感器,對迎角和側滑角等狀態量進行測量。但是需要注意的是,現代飛行器的飛行包線越來越大,飛行環境也更加復雜,外露的探針易受到各種外界干擾,測量精度難以得到保證。為了解決這個問題,美國、法國等國先后開展了關于嵌入式大氣數據傳感器(flush air data sensing,FADS)的研究,并已于近年運用在X-33、X-43A等飛行器上[1-3]。

和探針式大氣數據傳感器不同,FADS系統主要利用嵌入在機頭的壓強傳感器測量出的各點壓強值進行迎角、側滑角等狀態量的推導計算,有效地克服了傳統探針式傳感器的缺點和不足。

目前國內外針對FADS系統算法的研究主要可以分為最小二乘迭代法、神經網絡法、Kriging法、查表法和“三點法”。文獻[4]首次提出基于最小二乘迭代法的解算算法,但是此方法的弊端是實時性較差,且不易收斂,因此并沒有得到廣泛運用。文獻[5-6]提出基于神經網絡的解算算法,但是此方法需要大量數據支撐,一旦數據不充分或者不真實,測量精度就會受到很大影響。和神經網絡法類似,Kriging法[7-8]和查表法[9]都對樣本需求量較大,因此至今都未在飛行器上得到應用。除了上述方法外,NASA提出的“三點法”是迄今為止最為成熟應用范圍最廣的算法,此方法理論簡單且精度較高[10],但是其缺陷是在對系統冗余信號進行融合時,僅僅是簡單的算術平均,而并沒有充分考慮各組信號的差異性。

為了解決這個問題,以“三點法”為基礎,提出一種全新的方法提高FADS系統的測量精度。

提出一種利用正態云模型分析信號不確定性與隨機性，并結合多目標規劃方法計算客觀權重的全新方法提高FADS系統的測量精度。

1 問題描述

FADS系統是目前關于大氣數據傳感器研究中一個熱點部分,國內外很多機構均陸續開展了相關研究。其中,運用于X-33型飛機的FADS系統是目前公認最為成熟的,因此，以此系統為基礎開展相關研究。

1.1 FADS系統測量原理

根據亞聲速條件下的位勢流模型和超聲速條件下的牛頓流模型可以得到FADS系統表面壓力數學模型

Pi=qc[cos2(θi)+εsin2(θi)]+P∞

(1)

式中:Pi為第i個測壓孔的壓強值;qc為大氣動壓;ε為修正系數,受迎角α、側滑角β和馬赫數Ma同時影響,記為ε=f(α,β,Ma);θi為來流入射角,是測壓孔的位置角(圓周角φi和圓錐角λi)、迎角和側滑角的函數,記為

(2)

X-33型飛機的FADS系統中各測壓孔的布局和位置角如圖1和表1所示。

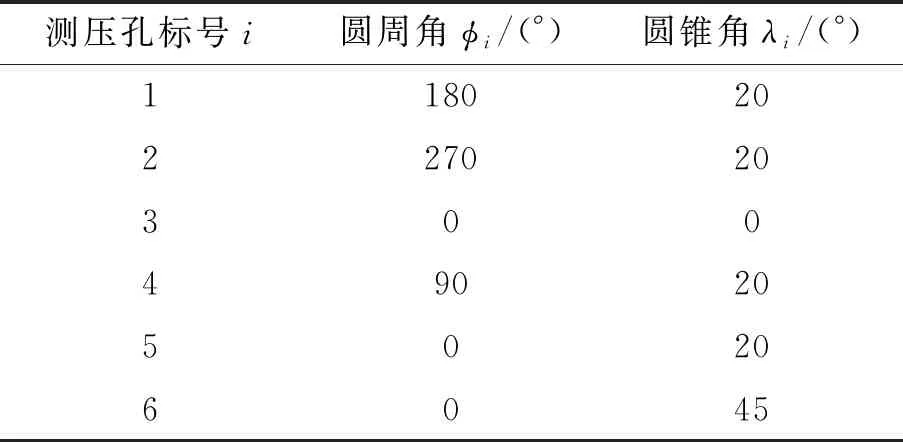
表1 各測壓孔的圓周角與圓錐角

考慮到2號孔和4號孔呈橫向分布,當飛機迎角改變時,2個孔的壓強值不會出現明顯變化,也就是說,這2個孔的壓強值并不能很好地反映迎角的改變。因此,本文主要利用呈縱向分布的4個測壓孔進行迎角的解析計算。

“三點法”的思想是從1,3,5和6號孔中按照排列組合的方式選出3個測壓孔,將其壓強值Pi,Pj和Pk帶入(1)式,可以得到

Pi=qc[cos2(θi)+εsin2(θi)]+P∞

Pj=qc[cos2(θj)+εsin2(θj)]+P∞

Pk=qc[cos2(θk)+εsin2(θk)]+P∞

聯立方程得到

(3)

式中,θi,θj和θk表示3個測壓孔的來流入射角。

整理(3)式得到

Γijcos2θk+Γjkcos2θi+Γkicos2θj=0

(4)

式中:Γij=Pi-Pj,Γjk=Pj-Pk,Γki=Pk-Pi。將(2)式代入(4)式,利用元素之間的一一對應關系消去側滑角,得到迎角計算公式

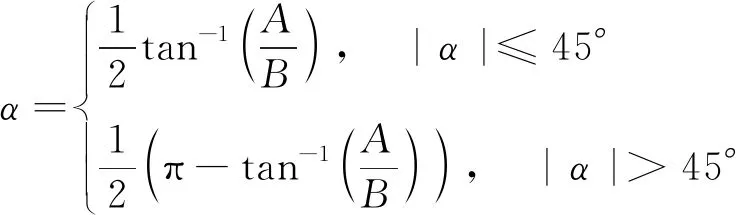
(5)

式中

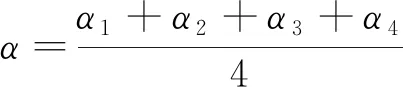
(6)

1.2 測量誤差分析

由(6)式可以看到,在計算最終迎角時傳統的“三點法”只是對4組解析值進行簡單的算數平均,但是在測量過程中,由于測量噪聲的干擾,α1,α2,α3和α4會圍繞著實際值呈現不同幅度的上下波動,也就是說,4組信號的置信度是不同的,要想得到精確的最終解,必須對每組信號的不確定性和隨機性進行具體分析,然后根據置信度的不同進行加權求和。

為了解決這個問題,正態云模型被用來對信號的不確定性和隨機性進行分析。

2 基于正態云模型的FADS改進算法

2.1 正態云模型定義

正態云模型是一種有效的定性概念和定量概念之間的轉化工具,一個標準的正態云模型由期望Ex、熵En和超熵He組成[11]。

設x是論域C的一次隨機實現,若x滿足x～N(Ex,En2),其中En～N(En,He2),那么x對C的確定度滿足

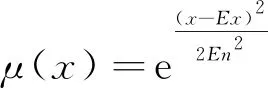
(7)

各云滴分布情況如圖2所示。

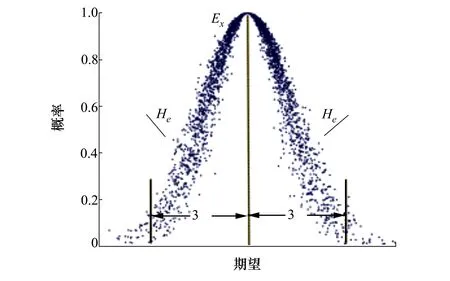
圖2 正態云模型云滴分布圖

2.2 云模型的基本運算規則

假設存在i朵云模型Yi(Exi,Eni,Hei):

1) 加法運算:

2) 集結算子:

Y1?…?Yi=

式中:wj為各云模型的權重值。

2.3 云發生器

2.3.1 正向云發生器

正向云發生器是定性到定量的映射。輸入是Ex,En,He以及需要產生的云滴數量N,輸出為N個定量云滴。

算法步驟:

1) 產生一個期望值為Ex,方差為En的正態隨機數xi;

2) 產生一個期望值為En,方差為He的正態隨機數En′;

3) 計算:yi=e-(xi-Ex)2/2(En′)2;

4) 令(xi,yi)為一個云滴;

5) 重復步驟1) ～ 4),直至產生N個云滴。

2.3.2 逆向云發生器

和正向云發生器相反,逆向云發生器是定量到定性的映射,輸入為N個定量云滴(xi,yi),輸出為Ex,En和He。

算法步驟:

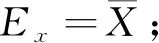
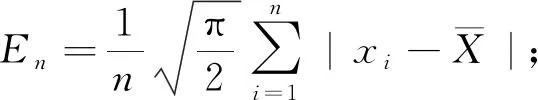
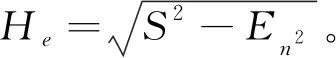
2.4 算法流程

算法流程如下所示:

1) 將測量信號轉化為正態云模型

在利用正態云模型對FADS系統的測量信號進行分析時,首先選取連續的N個采樣點,利用逆向云發生器對4組測量信號α1,α2,α3和α4進行處理,得到相對應的正態云模型Y1(Ex1,En1,He1)、Y2(Ex2,En2,He2),Y3(Ex3,En3,He3)和Y4(Ex4,En4,He4),其中參數熵和超熵分別表示信號的隨機性和不確定性。

2) 合成各正態云模型

在得到正態云模型Y1,Y2,Y3和Y4后,下一步就是利用2.2節中的集結算子對四組云模型進行融合,得到最終的合成正態云模型Y(Ex,En,He)。其中

3) 得到最終迎角值

在獲得了合成的正態云模型Y(Ex,En,He)后,利用2.3.1節中的正向云發生器對Y進行映射,得到對應的N個定量云滴,即為最終融合后的迎角值。

值得注意的是,在利用集結算子時,一個至關重要的問題是權重向量的選擇。在FADS系統的傳統迎角解算算法中,4組冗余信號的權重是主觀賦予的,皆為25%,但是這種方法的缺點是主觀性太強,缺乏客觀合理性,沒有充分考慮每組信號的差異,因此得到的結果難以令人信服。為了解決這個問題,從多目標規劃的角度出發,提出一種針對FADS系統測量信號的客觀權重計算方法。

3 多目標規劃計算FADS的信號權重

多目標規劃是數學理論的一個重要分支,主要研究多個目標函數在給定區域內的優化問題。由上文可以知道,FADS系統的4組冗余信號融合后的云模型為Y(Ex,En,He),其中

可以看到,一個關鍵的問題是如何得到1組合理的權重向量W={w1,w2,w3,w4},使得最終迎角的不確定性和隨機性最小且均值盡可能的接近4組信號的均值。由此得到以下3個目標函數

限制條件

經過對目標函數分析后可以發現,這是一個典型的多目標規劃問題,無法得到1組權重向量使其同時滿足(8)～(10)式。為了解決這個問題,我們采用松弛變量法和拉格朗日乘子法計算在給定區域內能夠最大程度同時滿足3個目標函數的權重向量。

算法步驟:

1) 構建總目標函數F(W)

F(W)=min·

2) 添加松弛變量Z={z1,…,z8}

本部分的目的是將不等式約束轉換成等式約束以便下一步計算。

3) 利用拉格朗日乘子法降階

在添加松弛變量后,此問題已經轉換成等式約束下的最小化問題。但是需要注意的是,維度也由R4增加至R12,計算將十分復雜。因此,一個有效的辦法是增加拉格朗日乘子μk,ν和γ,將問題轉換成無約束最小化問題。

將F(W,μ,v,γ)整理為

通過配方可以得到

知minψ(W,μ,v)的解為

因此:

4) 利用單純形法解無約束最小化問題

先對(11)式中的參數賦予初值,然后進行鑒別看是否是最優解,如果不是則轉換到另一改進后更優的基本可行解,再進行鑒別。通過優化迭代,直到(11)式實現最小值,得到最終的權重向量。

4 仿真驗證

4.1 FADS系統數據獲取

以往關于FADS系統的研究基本著重于介紹亞聲速及超聲速條件下的空氣動力學知識,對于具體的數據庫則很少公布。通過仿真驗證本文提出的利用正態云模型和多目標規劃對FADS系統的算法改進效果時,需要獲取算法的輸入數據即測壓孔的壓強值。為了解決這個問題,利用CFD軟件計算不同情況下測壓孔壓強值與迎角等狀態量的關系,然后建立插值表,這樣經過插值計算便可以得到給定狀態下的壓強值,隨后將壓強值代入算法,解算得到迎角等狀態量,通過比較給定的狀態量和解算得到的狀態量的差異對算法的性能進行分析。不同狀態下的各測壓孔的壓強值如圖3～4所示。

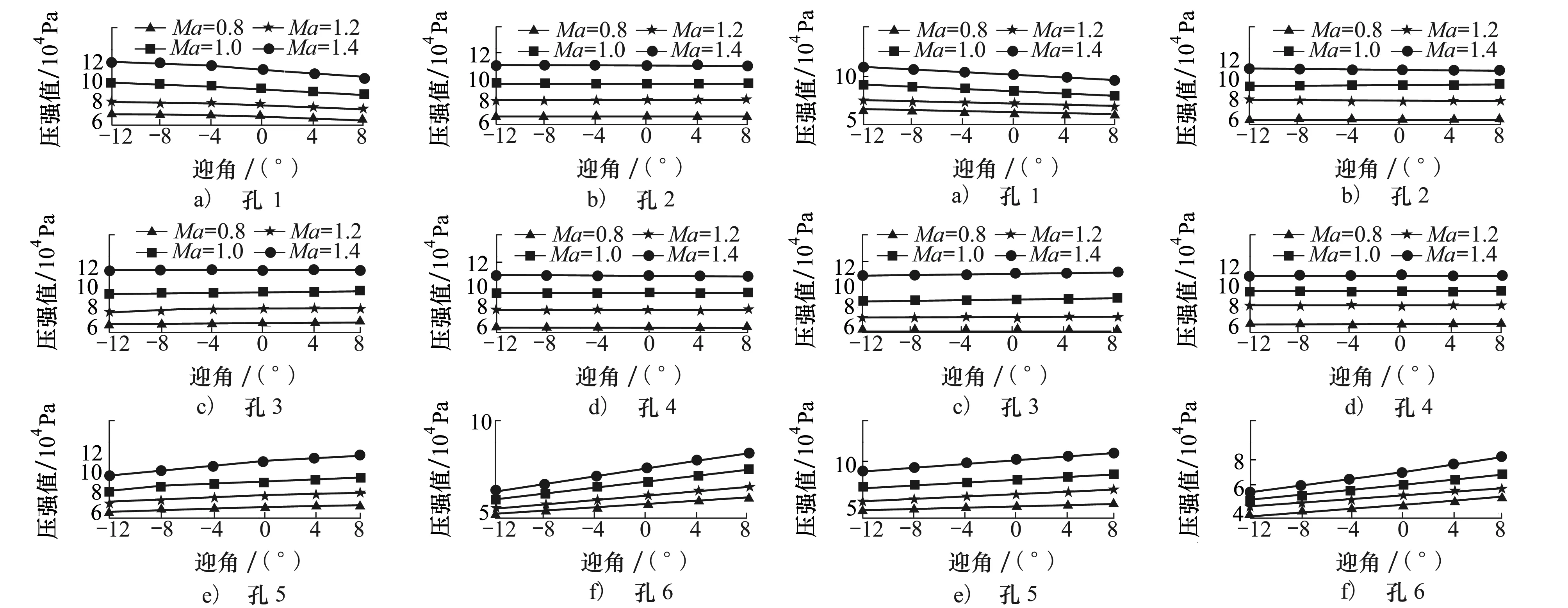
圖3 飛行高度10 000 m時的壓強數據 圖4 飛行高度12 000 m時的壓強數據

4.2 仿真算例

為了驗證所提出方法的有效性,設定飛機飛行速度Ma=1.3,飛行高度11 000 m,實際迎角αa=2°,側滑角0,各測壓孔上的測量噪聲為均值為0,方差300的高斯噪聲,仿真時長T=10 s,信號采樣頻率f=50 Hz,參數ε=10-6,單純形法參數β=0.5。

解算結果α1,α2,α3和α4如圖5所示,可以看到,由于受到測量噪聲的影響,4組解析值均圍繞實際值上下波動,但是各組信號的波動幅度和離散程度是不一致的。

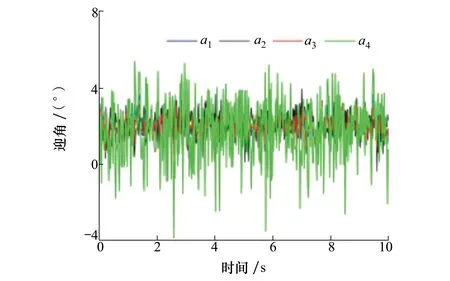
圖5 4組迎角解析值

計算步驟如下所示:

1) 生成云模型

利用逆向云發生器求得各信號參數值,如表2所示,其中云滴個數N=Tf=500。

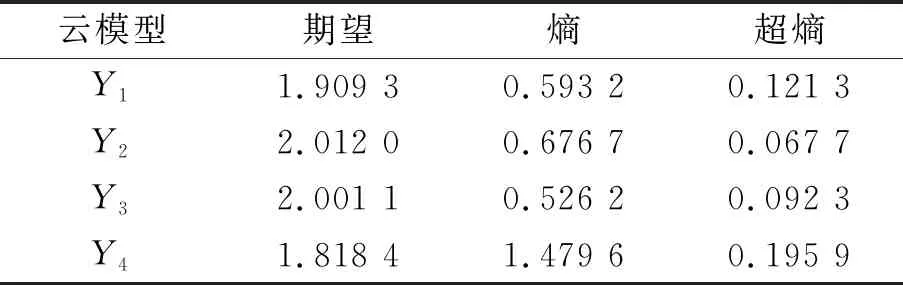
表2 各組信號參數值

利用正向云發生器得到云圖,如圖6所示。

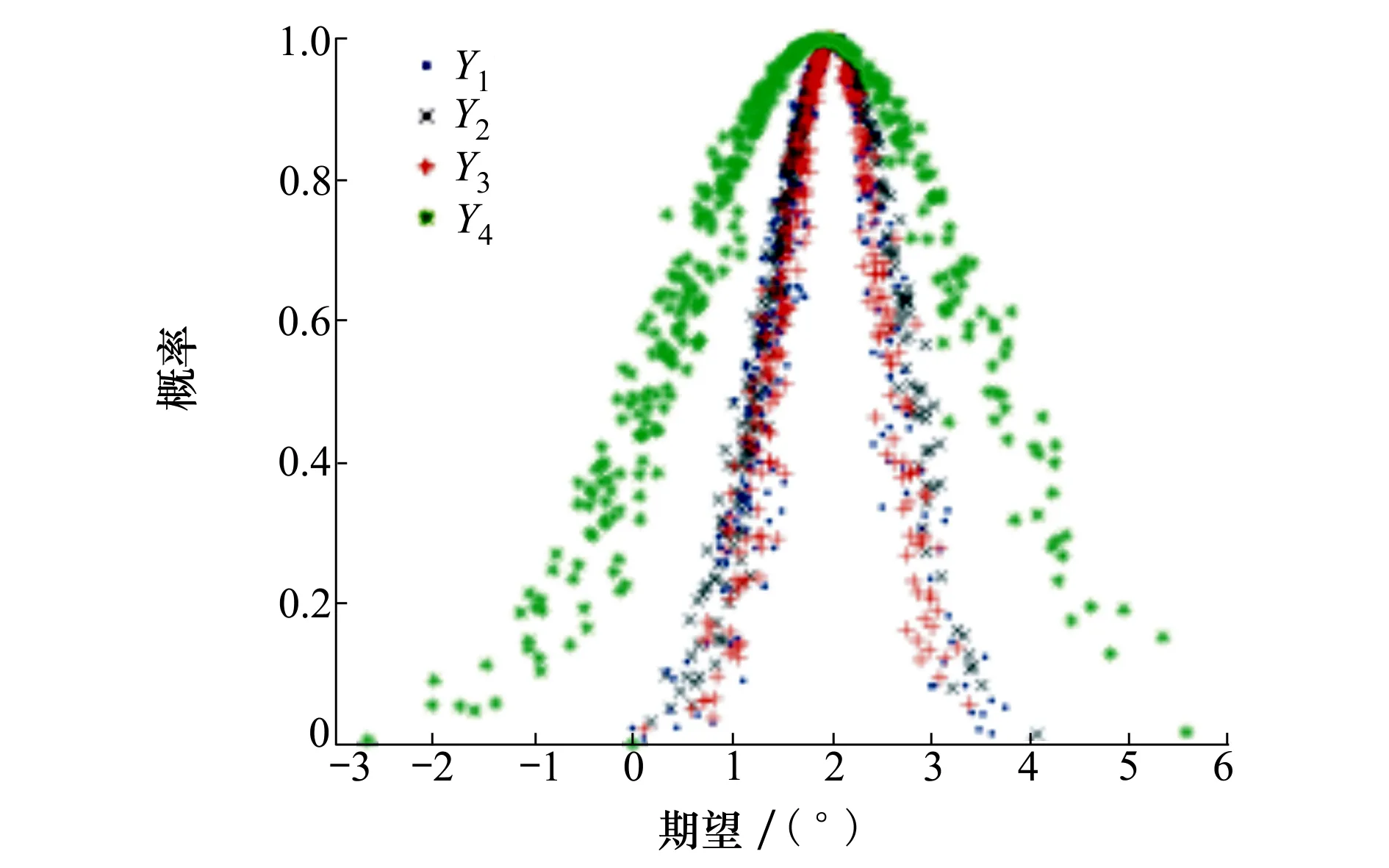
圖6 4組信號的正態云模型

2) 計算權重

利用多目標規劃中的松弛變量法和拉格朗日乘子法計算得到4組信號的權重向量為

W={w1,w2,w3,w4}={0.01,0.05,0.93,0.01}

3) 加權求和

利用集結算子和步驟2)中得到的權重向量,對4組云模型進行融合,得到最終云模型Y(1.998 9,0.553 0,0.093 2)。

4) 得到最終迎角值

利用正向云發生器對Y進行處理,得到500個云滴,即為最終迎角,如圖7中紅色曲線所示。

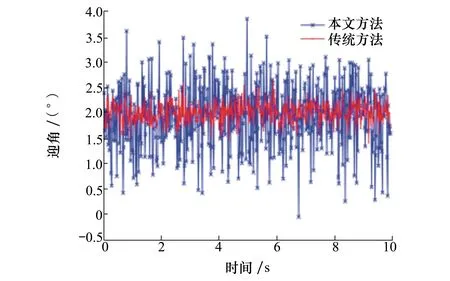
圖7 2種方法的計算結果

4.3 對 比

為了驗證所提出方法的有效性,在相同的仿真情況下將其與傳統方法進行比較分析,從圖7中可以看到,相較于紅線而言,采用傳統方法計算得到的藍色曲線的波動幅度明顯更大。表3是2種方法測量結果的特性表,主要包含平均值、標準差和方差等3種常用統計參數。可以看到,所提出方法的計算結果更接近于實際值,相較于傳統方法,測量精度提高了3.2%,數據離散程度降低了68.88%。

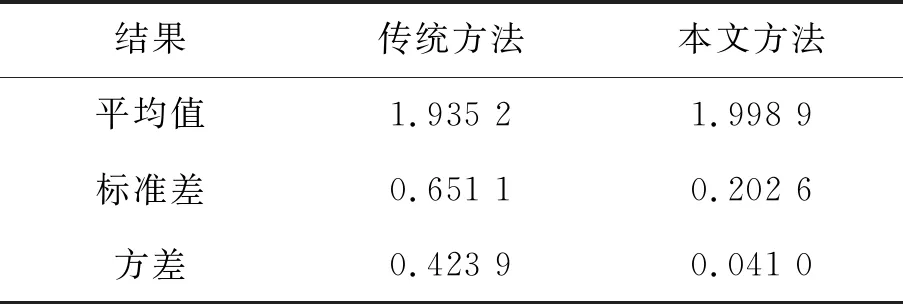
表3 2種方法測量結果特性表

為了進一步分析這2種方法在不同噪聲條件下的測量精度,分別將例子中的方差設置為3002,5002,7002,9002,1 1002,得到的測量精度結果如圖8所示。

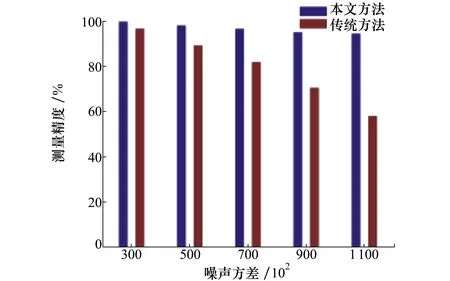
圖8 2種方法在不同情況下的測量精度

顯而易見,提出的方法在較高強度的噪聲條件下仍能保持較好的測量精度,具備更強的抗干擾性。

4.4 分 析

從上文可以看到,2種方法均可以在一定程度上跟蹤實際值,但是提出的方法明顯精度更高,信號離散程度更低,隨著噪聲方差的增加,相較于傳統方法,提出的方法仍然具備較好的測量精度。出現這種情況的主要原因是傳統方法僅對冗余信號進行簡單的算術平均,而沒有考慮每組信號所具備的不確定性和隨機性,而本文則利用云模型很好地體現了這2個特性,并在權重分配上充分考慮了每組信號的差異性。

5 結 論

針對FADS系統“三點法”測量精度不夠準確的問題,提出了一種改進的模糊融合方法,結合理論和數值結果分析,可以得出以下結論:

1) 提出的算法從系統數學模型出發,利用正態云模型深入分析系統冗余信號的不確定性和隨機性,然后借鑒多目標規劃思想提出一種新的權重計算方法,再利用云模型集結算子和權重向量對冗余信號進行融合,算法流程清晰,有利于工程實際中的應用。

2) 通過對比仿真不同方法在不同方差噪聲干擾情形下的結果,可知提出的方法在干擾比較強的時候仍然擁有更高的測量精度,抗干擾性更強。

本文所設計的方法主要利用多目標規劃思想重新計算信號權重,但考慮到此方法可能會遇到局部最小值的問題,因此未來將會針對改進權重計算方法開展研究。