考慮間歇期的飛機連桿式艙門收放機構競爭失效分析
劉敬一, 張玉剛, 莊新臣, 龐歡
(1.長安大學汽車學院, 陜西西安 710064;2.西北工業大學航空學院, 陜西西安 710072;3.清華大學機械工程學院, 北京 100091)
連桿式艙門收放機構在飛機中應用廣泛,諸如起落架艙門收放機構、貨艙門收放機構等。該類機構的失效會直接影響到飛機的安全性,確保該類機構的可靠運行尤為重要。本文所研究的某型飛機艙門的連桿式收放機構,存在突發型失效和退化型失效并存的現象,機構系統的實際失效是此二類失效相互競爭的結果。充分研究該機構的運行原理,結合機構的運行具備間歇期這一實際特點建立競爭失效模型,可以更為準確地對該機構可靠度的演化進行評估。
目前,在有關飛機機構的競爭失效研究方面,侯聿[1]研究了飛機起落架收放作動筒指型鎖的磨損;劉成業等[2]針對某型民用飛機艙門鎖結構變形現象,從接觸力角度開展了失效研究。以連桿機構為例,印寅[3]分析了某型起落架的動力學特性,并對起落架機構進行了可靠性研究;鄭怡[4]基于多體動力學,分析了發動機中連桿機構的動態應力,對連桿失效造成發動機的破壞性故障進行了研究。郭慶、劉曉娟等[5-6]分別研究了航空發動機的競爭失效行為,從壽命預測、可靠性評估和性能退化等不同角度對航空發動機的可靠性進行了研究。對于構件數目較多的連桿機構而言,各個構件的尺寸誤差和運動副中的間隙會產生較大的累計誤差,容易造成運動精度的不足,但當前有關飛機機構競爭失效的研究尚未涉及連桿類機構運動精度不足的問題。
在有關競爭失效模型的研究方面,Rafiee等[7]認為外界沖擊的出現會引起退化過程退化速率的改變,并綜合多種因素建立了的競爭失效模型。Qiu等[8]考慮退化過程的2個階段建立了競爭失效模型,并基于此分析了輸油管道的可靠性。Yang等[9]研究了處于競爭失效模式影響下的油氣輸送管道的維修保障策略。Hao等[10]對處于局部放電失效和漏氣失效2種失效模式影響下的氣體絕緣輸電保護裝置進行了研究,建立了競爭失效模型。齊佳[11]建立并用試驗驗證了性能退化自恢復產品的相關競爭失效模型。逯程[12]等則研究了競爭失效條件下對裝備的選擇性維修方法,考慮多種維修方式對處于多失效模式競爭作用下的系統進行了維修方式選擇的綜合優化。總的看來,現有的競爭失效模型并未考慮實際工作中“工作期”和“間歇期”相互結合的特點,需要建立新的模型。綜上,本文引入間歇期因素,建立了適用于飛機機構的競爭失效模型,利用泊松過程、Archard磨損模型分別對突發型失效和退化型失效進行研究;利用所建模型,對某型飛機連桿式艙門收放機構的結構組成、工作原理和失效行為進行深入研究,結果證明所建模型能夠有效地應用于該機構的競爭失效分析,同時可以推廣至其他具有相同特點的機械機構系統的研究之中。
1 基本描述
間歇期是區別于工作期的機構工作時間段,在此時間內機構面臨不同的環境特點,機構自身的性能退化速率也會發生變化。飛機機構通常處于兩類失效模式相互競爭的影響之下,一類為退化失效(例如機械軸的磨損、部件的老化),一類為因外界沖擊(例如意外的過大的工作載荷、振動沖擊引起的載荷等)導致的突發失效。對于突發失效,使用極限沖擊模型描述,即一旦有外界沖擊超過了系統的可承受量值,則發生突發失效;對于退化失效,使用考慮隨機參數的通用路徑模型描述,當退化量累計至一定量的時候,系統發生退化失效。考慮間歇期的系統競爭失效過程如圖1所示。
圖1時間軸中實線部分表示機構的工作期。當系統處于工作期的時候,退化量在較為快速地增加,同時工作期期間會有一定的概率出現外界沖擊(例如圖中T1時間段內的W1和W2),也就是說在工作期期間,系統會有一定的概率發生失效。每一次工作期的時長定義為T1,它的取值可取一個恒定值或隨機量值。圖1時間軸的虛線部分表示機構的間歇期,間歇期的意義為在此期間系統停止工作。處于間歇狀態系統的退化量因系統的“間歇”而增速減緩,同時“間歇”狀態的系統不會受到外界沖擊(例如圖中T2時間段并沒有任何外界沖擊出現)。每一次間歇期的時長定義為T2,其可取一個恒定值或隨機量值。相鄰的一個工作期和一個間歇期定義為一次工作循環(圖中T1時間段和T2時間段即可組合成一次工作循環),系統的壽命就是由若干個連續不斷的工作循環組成。
2 建模過程
2.1 突發失效建模
基于極限沖擊模型對突發失效進行描述,即當某次外界沖擊的量值大于系統的閾值之時,系統發生突發失效,因而系統在外界沖擊影響下的生存函數表示
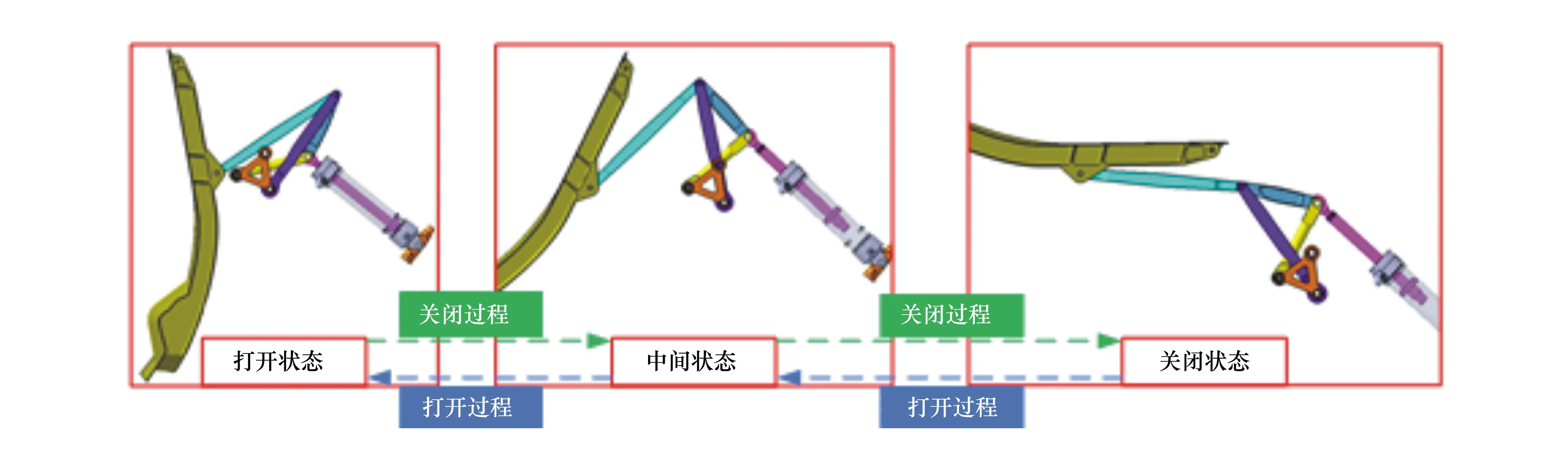
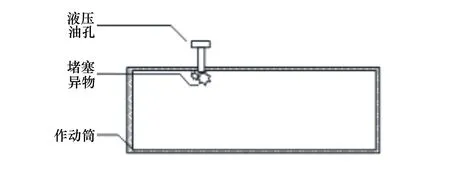
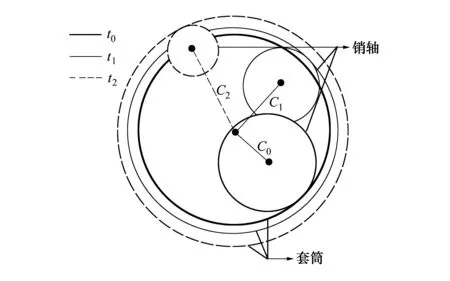
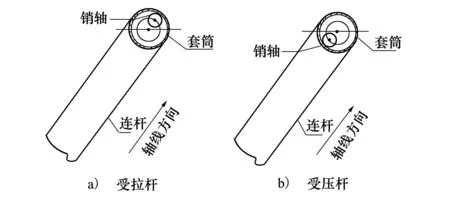
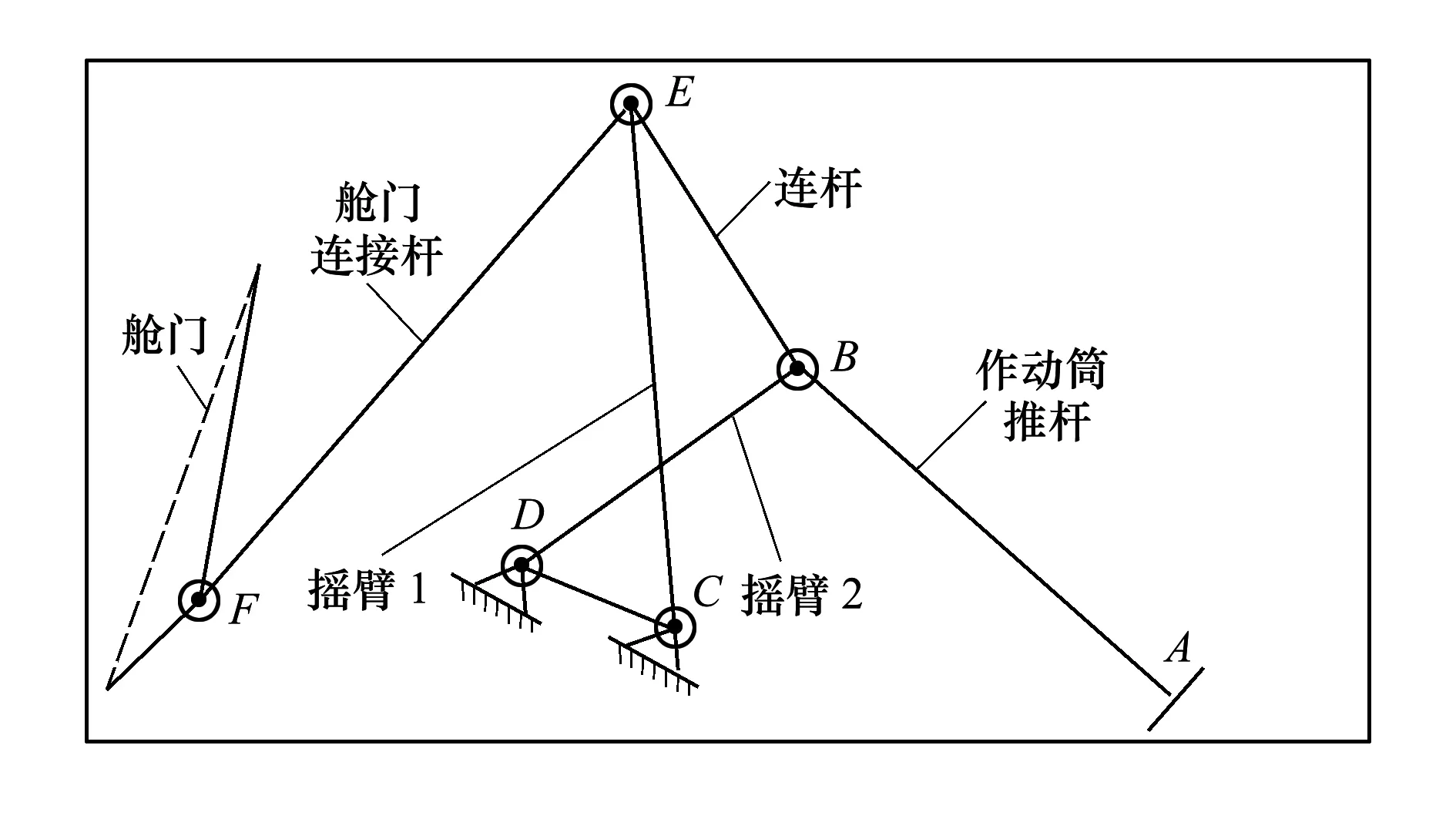
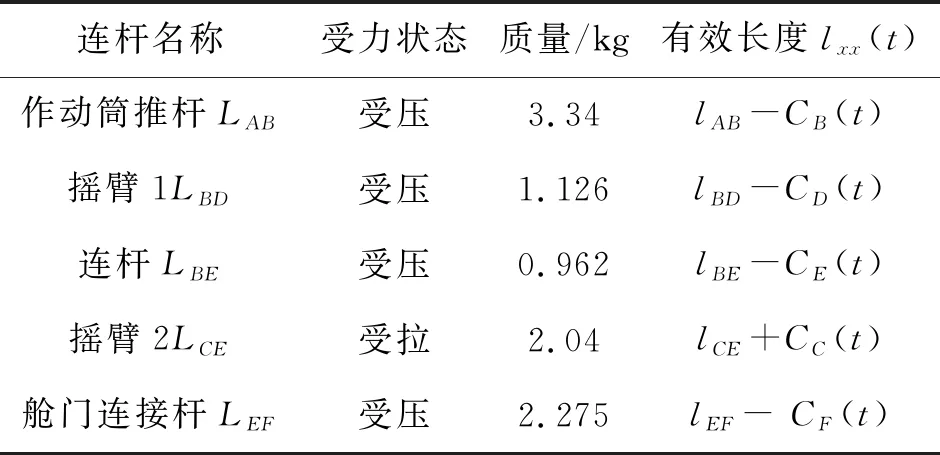
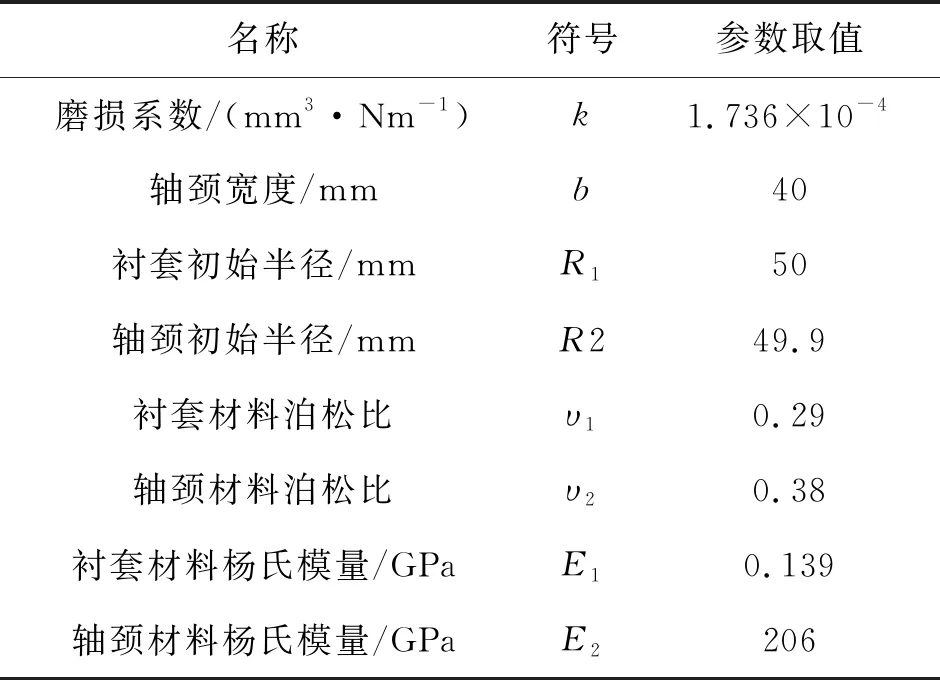
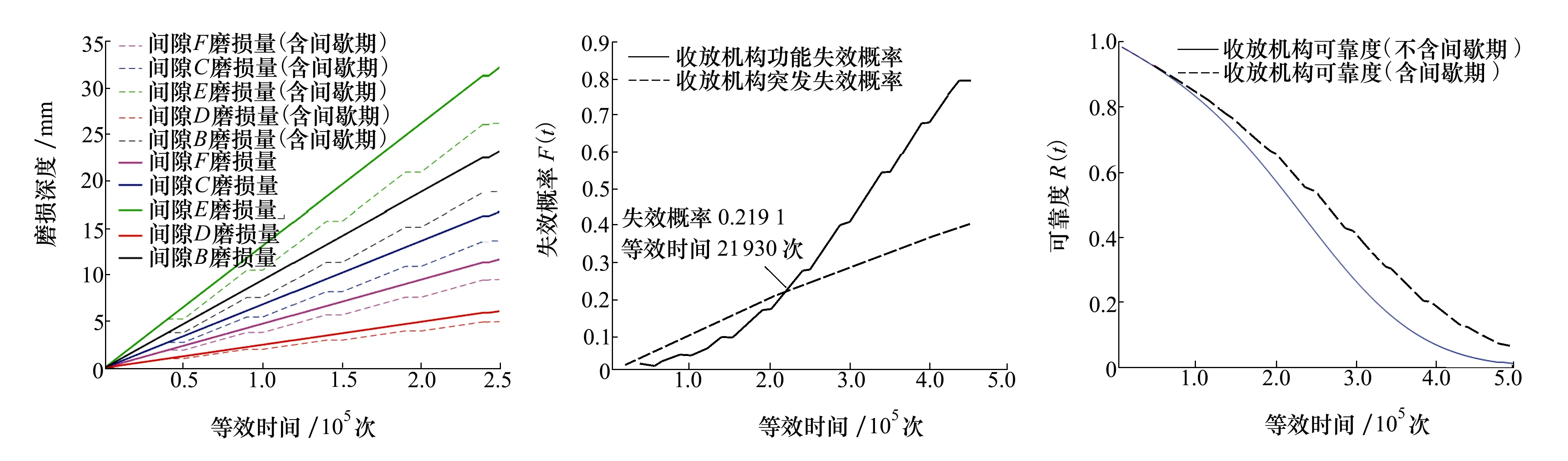
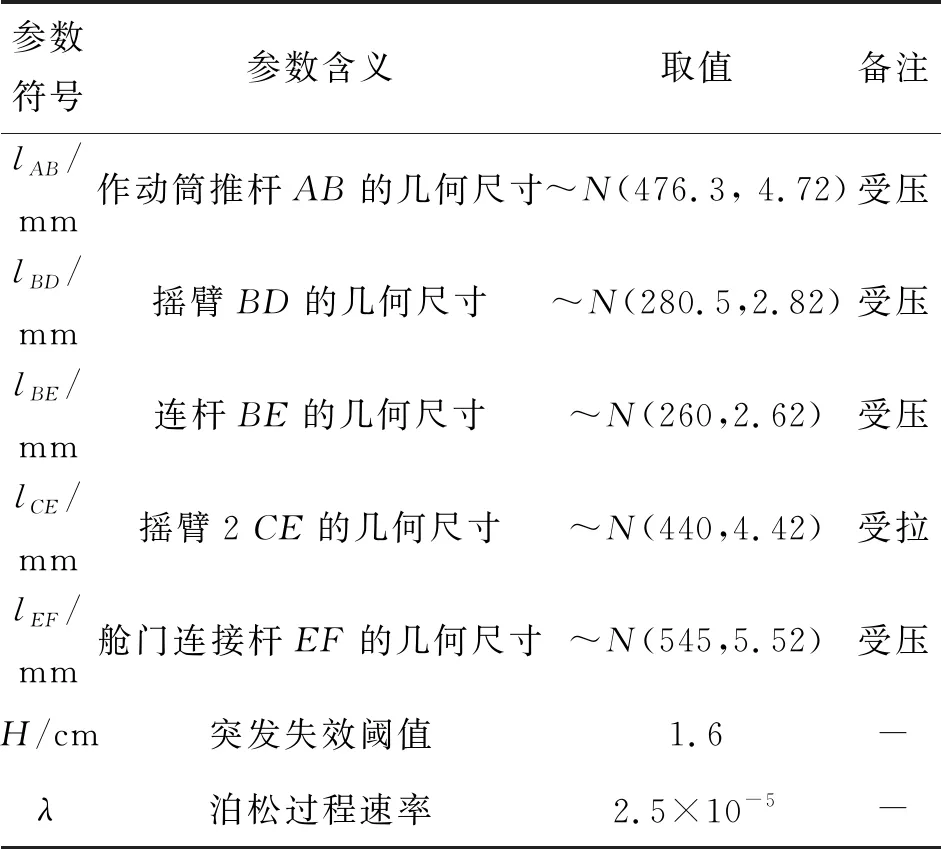
P(Wi (1) 式中:Wi為在時間ti所發生的外界沖擊的大小;H是系統突發失效閾值,代表抵御外界沖擊的能力。考慮一種特殊情況,如果外界沖擊和系統閾值皆是符合正態分布的隨機變量,上述生存函數表達式變為 (2) RH(t)=P({W1 (3) 式中:n表示工作循環的次數;T1和T2分別表示一次工作期和間歇期的持續時長。當n取固定值的時候,公式(3)中的表達式(Ⅰ)的取值會隨著t而發生變化,這是因為工作期期間系統會受到外界隨機沖擊的影響,有可能發生突發失效,具體的概率值會隨著時間發生變化;而表達式(Ⅱ)則會保持定值,這是因為間歇期并未有外界沖擊發生,系統的生存概率等于上一個工作期最后時刻的生存概率。 退化量會在工作期期間隨著時間而累積,因系統在間歇期未處于使用狀態,故而退化量也保持定值。總的退化量Xs(t)包括因系統使用而產生的無法避免量X(t),我們稱之為“純退化”,以及因外界沖擊導致的退化量增加S(t),我們稱之為“額外退化”。在退化軌跡模型中,純退化可以表示為X(t)=φ+γt,類似的,當考慮間歇期的時候純退化進一步表示為 (4) 式中:φ為退化量的初值;γ1和γ2分別表示工作期和間歇期退化量的增加速率,三者一般是符合特定分布的隨機變量。而因外界沖擊所導致的額外退化可表示為: (5) 式中,N(t)是一計數過程,表示截止時刻t所發生的沖擊的次數,使用速率為λ泊松過程來描述。綜合上述兩表達式,系統總的退化量表示為 (6) 如果系統不發生退化失效,則要求總的退化量不超過系統的許用閾值,此時的生存概率表示為 (7) 基于卷積,上述表達式進一步推導為 RX(x,t)= (8) 圖2為該機構的收放過程示意圖。機構可以劃分為作動筒、連桿機構和艙門三大部分。作動筒為動力源組件為整個機構提供動力;連桿機構承擔連接和傳動的作用;艙門屬于輸出組件,在動力源和連桿的帶動之下,實現打開和關閉狀態的機構功能。該收放機構的功能要求在既定的時間內完成艙門的打開和關閉動作,由于作動筒性能退化和運動副間隙演化,導致該機構存在2個失效模式: 圖2 連桿式艙門收放機構功能示意 失效模式1:作動筒堵塞導致的驅動力下降。作動筒失效的最主要原因之一是因液壓油中異物導致的阻塞[13],進而導致作動筒可輸出液壓力下降,從而造成機構的失效。根據文獻[14]可知,導致堵塞的異物來源可能是外界環境帶入,也可能是由于作動筒筒壁和活塞桿之間的摩擦造成,這個過程可以用沖擊模型來描述。圖3為該失效模式示意圖,屬于突發失效; 圖3 機構失效模式1 失效模式2:艙門關閉不到位。艙門是由作動筒驅動一系列的連桿運動達到關閉位置,只有達到滿足要求的既定位置,艙門的關閉功能才可視為完成。但由于隨機性和磨損的存在,隨著使用次數和時間的延長,運動副的間隙會增大,進而有可能導致艙門無法關閉到位,當艙門的實際位置的轉角和要求轉角之間的誤差超過一定程度的時候,就可視為功能無法完成。圖4為該失效模式示意圖,屬于可退化的功能失效。 圖4 機構失效模式2 3.2.1 突發型失效建模 導致作動筒堵塞異物尺寸的大小和出現時間都是隨機的,可以把異物看作是量值和到來時間均不確定的外界沖擊[14];只有達到一定尺寸的異物才會導致堵塞的發生。以Wi表示出現在液壓油中異物的尺寸大小,H表示能夠造成作動筒堵塞的臨界尺寸值,該機構不發生突發失效的概率表示為: P(Wi (11) 式中,Wi是獨立同分布(independent identically distributed)的變量,表示每次出現異物的隨機尺寸值。使用泊松過程表示異物的隨機出現時刻,綜上,機構不發生突發失效的概率表示為 式中:N(t)表示泊松過程,用于衡量異物出現時刻的不確定性;λ為泊松過程的速率,表示異物出現的頻繁程度,速率越大則出現異物的頻率越高。不發生突發失效要求沒有異物出現(即式中i取值為0)或出現的異物尺寸皆小于閾值H。 3.2.2 退化型失效建模 1) 連桿有效長度的表示 圖5為連桿機構兩桿件之間的鉸鏈式運動副間隙隨磨損而變化的簡化示意圖。實線、點劃線和虛線分別表示初始時刻t0、中間時刻t1和最終狀態t23個時間點銷軸和套筒的尺寸變化(為了示意圖的展示效果,尺寸進行了相應的放大),隨著時間的演化,銷軸和套筒因磨損發生了尺寸的改變,運動副間隙C0,C1和C2也逐漸增大。 圖5 鉸鏈式運動副間隙增大示意圖 根據等效長度理論[15],機構連桿參與運動的等效長度由連桿本身尺寸長度、間隙尺寸和連桿所受拉壓狀態共同決定。等效桿長理論可簡單表述為,參與機構運動傳遞的連桿等效長度等于連桿的實際長度加上(減去)間隙長度,表示為l′=l±C=l±(R1-R2),其中l為連桿的實際幾何長度,l′為連桿參與運動傳遞的有效長度,C為間隙的尺寸,R1和R2分別表示銷軸和套筒的半徑。 如圖6所示,當連桿處于受拉狀態的時候,實際參與運動傳遞的長度會因間隙的存在而增大,有效長度表示為l+C,類似地,當連桿受壓時,有效長度會因間隙的存在而減小,表示為l-C。 圖6 連桿有效長度示意圖 2) 運動副磨損及間隙演化建模 連桿機構鉸鏈磨損是影響傳動精度的重要因素,Archard模型[16],可以對磨損體積、滑動速度、垂直載荷以及材料硬度等參數進行解釋,該模型已經得到了廣泛的認可和應用。Archard磨損模型的計算公式表示為: (13) 式中:h表示磨損深度,當考慮均勻磨損的時候h等同于間隙C的變化量;s為相對滑移距離,k為無量綱的磨損系數,H為較軟材料的硬度,p為接觸應力,E為材料相應的楊氏模量。接觸應力的大小可以根據赫茲接觸理論計算求得,即 (14) 式中:F為單位長度的載荷;R1和R2為銷軸和襯套的半徑;υ為材料的泊松比。 相對滑移距離可以根據幾何關系推導得到,即 (15) 式中:φ為一個運動周中銷軸和襯套的相對轉角;n為運動的周期數。 綜合上述各表達式,磨損的深度可以計算為 (16) 式中:p(t)和ω(t)分別為接觸應力和轉動角度隨時間的函數,可以通過機構的動力學分析得到。根據有效長度理論,間隙的演化使得連桿參與運動的有效長度發生改變。 3)機構功能失效建模研究功能失效的表現形式為“艙門無法關閉到位”,選取艙門從打開位置到關閉位置時候所轉過的角度作為功能表征量,根據艙門工作要求,滿足規定的旋轉角度為A0=120°。為了提高計算效率,使用一階響應面構造艙門的功能表征函數,構造步驟如下: step1 依據運動原理搭建參數化機構動力學仿真模型; step2 按照各輸入參數的分布(見表1~3)進行拉丁超立方抽樣,將抽樣值代入仿真模型,得到成組的輸入輸出; step3 利用step2中得到的結果進行響應面的構造并進行精度驗證。 構造得到的連桿式艙門收放機構功能表征量的響應面函數為: 式中:A(t)為艙門的關閉角度;l(t)表示間隙的退化影響連桿的有效長度。當艙門實際旋轉的角度A(t)和要求角度A0的偏差超過許用偏差δ的時候,艙門發生功能退化失效。因此,艙門的功能滿足要求即不發生功能退化失效的公式表達為: RF(t)=P(|A(t)-A0|<δ) (18) 式中:A0為理想狀態艙門關閉時所旋轉的角度;A(t)為艙門實際所旋轉的角度,其具體的取值由功能表征函數計算決定;δ為許用誤差。 3.2.3 機構可靠度及其演化規律 若要該連桿式收放機構不發生失效,則需突發失效和功能退化失效都不能發生,綜合公式(12)和公式(18),推導得到機構的整體可靠度為 特殊的,若艙門的實際旋轉角度A(t)服從正態分布 ,上述表達式進一步推導為: 圖7為該連桿收放機構的簡化示意圖,結合艙門關閉狀態各個連桿的拉壓狀態,各連桿的有效長度如表1所示。連桿式艙門收放機構并非總處于運動過程之中,而是會有一段時間的間歇狀態。由于相對運動的停止,處于間歇時的連桿式艙門收放機構不會發生進一步的磨損。結合實際的工況,該連桿式艙門收放機構每有40 000次開閉(即工作狀態的等效時長)就會有10 000次等效時長(即間歇狀態的等效時長)的間歇狀態,當機構處于間歇狀態時,各個運動副的磨損不再隨時間增加。根據公式(13)~(16),可以計算得到連桿式艙門收放機構各鉸鏈的磨損規律,參數的含義和取值如表2所示。 圖7 連桿式艙門收放機構簡化示意圖 表1 艙門收放機構連桿狀態 表2 艙門收放機構磨損相關參數 圖8為各個鉸鏈間隙磨損量的演化示意圖。圖中縱坐標為磨損深度,橫坐標為使用艙門收放機構的開閉次數所表示的等效時間。 圖8 各處間隙磨損量演化示意圖 圖9 失效概率演化示意圖 圖10 連桿式艙門收放機構可靠度演化示意圖 將表3參數帶入公式(12)~(20),可以計算得到該連桿式艙門收放機構各失效模式的失效概率(見圖9)和系統可靠度及其演化規律(見圖10)。從圖9看出,等效工作時間為21 930次時,2種模式的失效概率相同,而不考慮間歇期情況下2種模式失效概率相同時對應的等效工作時間約提早至2 000次。從圖10可以看出,考慮間歇期后的收放機構其退化速率降低,可靠度演化速率隨之減緩。在等效工作時間為21 930次時,相對應的可靠度約相差20%。 表3 連桿式艙門收放機構參數取值 本文建立了考慮間歇期的競爭失效模型,并以某型飛機連桿式艙門收放機構為研究對象,分析了其可靠度演化規律。連桿式收放機構處于突發失效(因作動筒突然堵塞導致)和功能退化失效(因運動副間隙演化導致的運動精度不足)2種失效模式的競爭作用之下,基于本文研究,做出如下結論和展望: 1) 機構鉸鏈磨損并非直接導致機構失效,而是產生的誤差通過功能表征函數進一步傳遞至功能表征量,引起旋轉角度不符合要求引起功能失效; 2) 間歇期的存在改變了各個鉸鏈間隙的磨損過程,使得2種模式失效概率相等所對應的等效時間由約2 000次延長至21 930次。在此時刻后,功能失效成為艙門收放機構的主要失效模式,需在維護保養工作中著重關注; 3) 間歇期使得機構可靠度退化減緩,在等效時間為21 930次時,減緩程度約20%; 4) 本文所建考慮間歇期的競爭失效模型可推廣至其他具有間歇期特征的系統可靠性分析中,例如運載車輛傳動系統、電腦存儲系統等。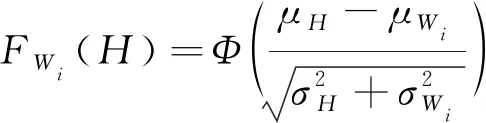
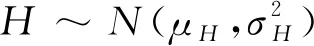
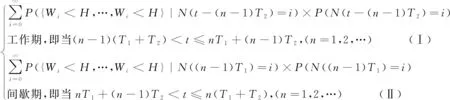
2.2 退化失效建模
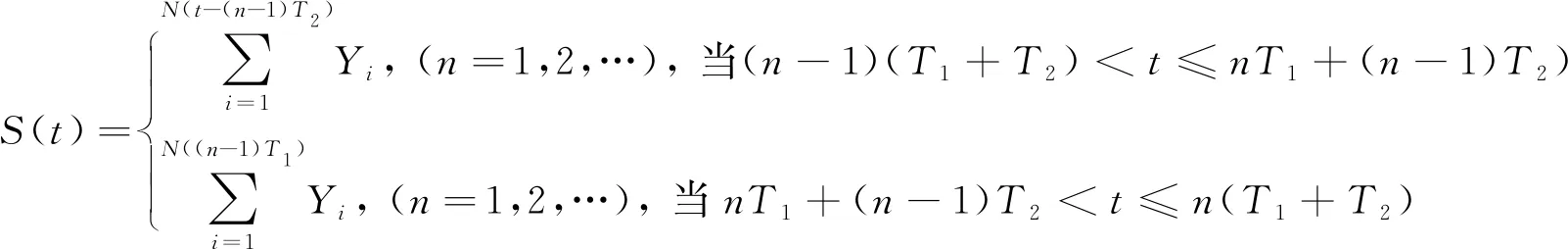
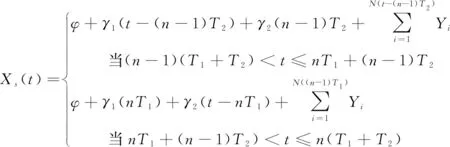
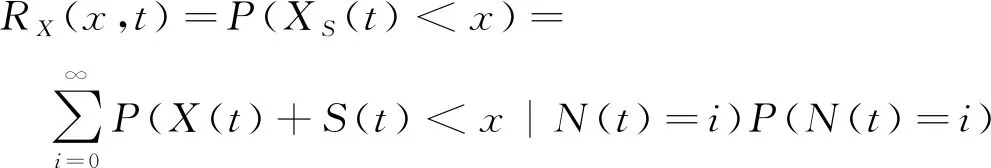
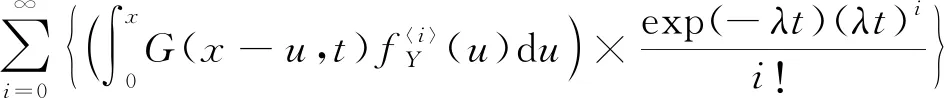
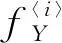
2.3 考慮間歇期的競爭失效系統可靠性及其演化建模
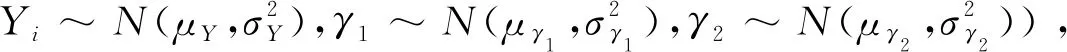
3 某型飛機連桿式艙門收放機構競爭失效研究
3.1 機構工作原理及失效模式

3.2 考慮間歇期的連桿式艙門收放機構競爭失效建模
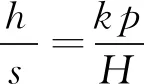
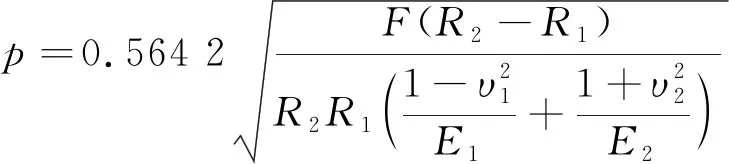
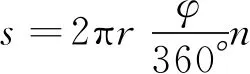
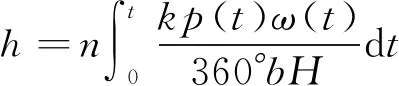
3.3 計算結果
4 結 論

