基于漲落耗散理論的能量本征態(tài)規(guī)范研究

郭 凱

（華能武漢發(fā)電有限責(zé)任公司，湖北 武漢 430415）

0 引言

熱漲落是物理學(xué)中的基礎(chǔ)現(xiàn)象之一。基于統(tǒng)計物理理論，漲落耗散理論（fluctuation dissipation theorem，F(xiàn)DT）主要描述分子的隨機運動導(dǎo)致系統(tǒng)的能量損失，在遠(yuǎn)離熱力學(xué)平衡條件（熵最大值）下，系統(tǒng)的熵會在某一定時間中增加或減少的相對概率［1］。盡管分子運動的動能很小，但是，在超精密測量領(lǐng)域中，例如，地基激光引力波探測器，分子運動導(dǎo)致的熱漲落占據(jù)主要的噪聲貢獻(xiàn)［2-4］。熱力學(xué)第二定律預(yù)測了一個獨立系統(tǒng)的熵應(yīng)該趨向增加，直到其達(dá)到平衡為止。但是，在統(tǒng)計力學(xué)被發(fā)現(xiàn)后，物理學(xué)家才發(fā)現(xiàn)第二定律只是統(tǒng)計上的一種行為，因此，應(yīng)該總有一定的概率使得獨立系統(tǒng)的熵會自發(fā)性地衰減；而漲落定理準(zhǔn)確地量化了此概率［5］。這個定理與物理學(xué)中的許多現(xiàn)象、概念和定理有著密切的聯(lián)系，而且廣泛應(yīng)用于布朗運動、磁介質(zhì)磁化、電介質(zhì)極化、回路中的熱漲落導(dǎo)致的電噪聲、等離子體、固體中的光散射以及各種輸運過程等問題［6］。

漲落耗散是熱平衡態(tài)的理論形式之一，它提供物體的反應(yīng)（即耗散，dissipation）與關(guān)聯(lián)（即漲落，fluctuation）的統(tǒng)一關(guān)系［7-8］。獨立的量子多體系統(tǒng)是否接近于熱平衡態(tài)是一個值得深入研究的問題，例如，在量子熱化過程中，關(guān)于超冷原子的探測與應(yīng)用的理論研究和實驗研究都引起人們的廣泛興趣。一個獨立的量子系統(tǒng)進入一個穩(wěn)態(tài)后的緩和態(tài)已經(jīng)在大范圍系統(tǒng)與初態(tài)之間得到驗證。熱化過程則需要穩(wěn)定態(tài)與平衡微正則態(tài)之間存在區(qū)別。隨著平衡動力學(xué)被詳細(xì)的量化，熱平衡系統(tǒng)的動力學(xué)反應(yīng)函數(shù)和相關(guān)函數(shù)不是相互獨立的關(guān)系，而是彼此之間緊緊聯(lián)系。漲落耗散理論已經(jīng)被用于區(qū)別平衡與非平衡動力學(xué)［9］，以及用于測量微觀量子系統(tǒng)的溫度［10-11］。

本 征 熱 化 假 說（eigenstate thermalization hypothesis，ETH）彌補了穩(wěn)態(tài)與Gibbs 態(tài)之間的理論空白。ETH表示局域可觀測量的矩陣元素在哈密頓本征態(tài)中的假說條件。在這種條件下，可觀測量的期望值與微正則態(tài)系統(tǒng)平衡均值一致。在不可積分系統(tǒng)中，ETH 已經(jīng)被廣泛驗證，且可觀測量的矩陣元素顯示了ETH的統(tǒng)計性質(zhì)。在量子湮滅與熱動力作用之后的熱化過程也能在ETH 條件下得到很好的解釋。在一個獨立的量子系統(tǒng)中，大量的工作已經(jīng)或正在研究量子熱力學(xué)與漲落和耗散之間的關(guān)系。文獻(xiàn)［12］和文獻(xiàn)［13］已經(jīng)研究了非熱可積量子系統(tǒng)的弛豫動力學(xué)性質(zhì)。基于Lieb-Robinson 邊界條件［14］，文獻(xiàn)［15］提出了一種靜態(tài)與動態(tài)關(guān)聯(lián)的爭議關(guān)系。文獻(xiàn)［16］研究了一種獨立量子系統(tǒng)的FDT，它涉及到可觀測量的期望值的關(guān)系，這相當(dāng)于全量子力學(xué)FDT 的經(jīng)典極限［17-18］。文獻(xiàn)［19］已經(jīng)證明單個可觀測量的FDT符合本征熱化假說，兩個不同可觀測量的FDT 則需要假定隨機變量的行為，本征熱化假說也需要進一步得到驗證。

在Gibbs 態(tài)中，漲落耗散理論是熱平衡系統(tǒng)的重要特征之一。但是，現(xiàn)在的問題是能否在一個能量本征態(tài)的獨立量子系統(tǒng)中驗證漲落耗散理論的合理性與正確性？在本征熱化假說條件下，可通過能量本征態(tài)或?qū)蔷仃嚨碾p時相關(guān)函數(shù)計算得到規(guī)范的表達(dá)式。在無限大系統(tǒng)條件下，這種規(guī)范表達(dá)式既是FDT 的充分條件，也是FDT 的必要條件。此外，在有限大系統(tǒng)中，這種規(guī)范表達(dá)式也能獲得有限的相關(guān)關(guān)系。即，無論是有限大系統(tǒng)，還是無限大系統(tǒng)情況下，能量本征態(tài)的規(guī)范表達(dá)式可以通過漲落耗散理論進行合理的解釋［20］。

1 能量本征態(tài)的規(guī)范研究

1905年，愛因斯坦發(fā)表論文討論了一定溫度條件下，懸浮于液體介質(zhì)中微小粒子的運動規(guī)律，即布朗運動［21］。因此，漲落耗散的研究可以追溯愛因斯坦。若液體介質(zhì)中微小粒子的濃度n是不均勻的，那么液體介質(zhì)會存在梯度為p的滲透壓力。由于滲透壓力的作用，微小粒子就從濃度高的地方流向濃度低的地方，若把布朗運動粒子作為理想氣體，其壓力梯度p與粒子濃度n的關(guān)系可表示為

事實上，做布朗運動的粒子由于熱運動作用，存在兩種流動形式，分別定義為擴散流和漂移流。擴散流是由粒子濃度不均勻?qū)е拢屏魇鞘芰Φ淖饔卯a(chǎn)生。因此，可把粒子平衡式（2）當(dāng)作擴散流和漂移流的平衡，即有關(guān)系式

式（4）中，μ表示粒子的遷移率；μG表示粒子的漂移速度，它主要是由于重力G、粒子與介質(zhì)的摩擦決定；D表示粒子的擴散系數(shù)。通過詳細(xì)比較式（3）和式（4）之間的差異，可以得到

在統(tǒng)計物理學(xué)中，在滿足給定宏觀條件系統(tǒng)的所有穩(wěn)定狀態(tài)下，宏觀物理量的定義為相應(yīng)微觀物理量的平均值，其數(shù)學(xué)表達(dá)式為

式（6）中，Bs表示微觀物理量；ρ表示微觀物理量的密度分布；S表示分布區(qū)域。采用偏差平方的平均值表示B對Bˉ的漲落，得到漲落耗散的準(zhǔn)熱力學(xué)理論關(guān)系式

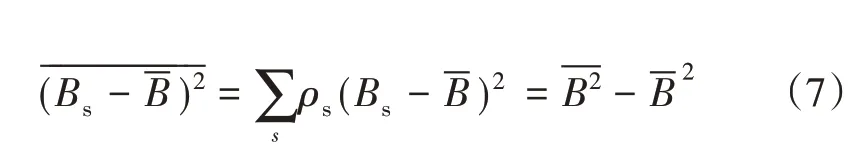
因此，式（5）是愛因斯坦關(guān)于漲落耗散理論研究的雛形。其核心思想是原子的獨立性，即原子的數(shù)目、原子的大小都具有有限性，這都可能在漲落耗散現(xiàn)象式（7）中顯現(xiàn)出來，這種漲落耗散理論的概念正是統(tǒng)計物理學(xué)中表現(xiàn)粒子的規(guī)律性及其核心思想。

2 漲落耗散理論應(yīng)用探討

熵增原理可以簡單地描述為孤立系統(tǒng)經(jīng)絕緣過程由一狀態(tài)達(dá)到另一狀態(tài)，熵值只可能增大，不可能減少。這個定律最先在1864 年首先由克勞修斯提出。在統(tǒng)計力學(xué)被發(fā)現(xiàn)后，物理學(xué)了解到熱力學(xué)第二定律只是一個統(tǒng)計規(guī)律。波爾茲曼用大數(shù)定律在理論上證明了熵增原理［22］。

但是，學(xué)者發(fā)現(xiàn)應(yīng)該有一些概率會使得獨立系統(tǒng)的熵自發(fā)性地減少。為了證明該現(xiàn)象，波爾茲曼從而提出了漲落理論。漲落定律準(zhǔn)確地量化了那些使熵自發(fā)性地減少的概率。其中，在討論宏觀系統(tǒng)時，漲落力通常可以忽略；而在討論微小系統(tǒng)時，熵增定律往往不適用［23］。

此外，漲落是種理論，也是一個物理現(xiàn)象，最常見的漲落現(xiàn)象是布朗運動［24］。布朗用顯微鏡觀察到一些比分子大數(shù)百億倍的物體，如花粉。花粉在永不停息地作不規(guī)則運動，這種運動被稱為布朗運動。布朗運動是由漲落引起的，花粉會受到周圍氣體或液體分子不停的撞擊。如果各方向撞擊機會均等，在合力為零的情況下，花粉是不會動的［25］。但實際上，由于漲落能的影響，花粉周圍的區(qū)域內(nèi)氣體或液體分子的分布是不均勻的。從而使得撞擊產(chǎn)生的合力并不為零，而是一種大小和方向隨機變化的漲落力，這種力推動花粉不停移動。

一些精密測量儀器的微小部件也會發(fā)生布朗運動，這影響了測量精度，所以國內(nèi)外學(xué)者對此開展了廣泛研究［26］。以懸鏡式電流計為例，在沒有電流或電流沒有變化的情況下，懸掛在石英絲上的鏡子，會保持不停擺動，從而使得測量數(shù)據(jù)產(chǎn)生明顯誤差［27］。以往在研究這個問題時，考慮的是如何減少漲落力的負(fù)作用。而考慮漲落力的利用，可使該問題產(chǎn)生正面意義，并研究能量在這一過程中的利用。如當(dāng)小鏡子在漲落力作用下轉(zhuǎn)動一定角度時，石英絲就擁有彈性勢能。石英絲這種壓電晶體被扭轉(zhuǎn)還能產(chǎn)生電能等［28］。這些能量的數(shù)值不大，但從本質(zhì)上說它是可以傳遞和轉(zhuǎn)化的自由能。負(fù)熵和自由能本來就是密不可分的，漲落產(chǎn)生了負(fù)熵因而產(chǎn)生了自由能。

海洋深處有一種靠波力發(fā)電機提供能量的航標(biāo)燈［29］。圖1 所示是一種簡單的波力發(fā)電機的結(jié)構(gòu)原理，圖中A是裝置外的密封浮箱；B是用彈簧與水箱聯(lián)在一起的重物；C是一個可雙向轉(zhuǎn)動的發(fā)電機，定子固定在浮箱上，轉(zhuǎn)子的齒輪和重物相配合。對于波力能發(fā)電機而言，當(dāng)海潮沖擊浮箱時，將所含的動能傳遞給浮箱，并使浮箱產(chǎn)生位移。但箱內(nèi)的重物并沒受到直接沖擊，且由于彈簧的緩沖作用以及自身慣性影響，這浮箱與重物之間就產(chǎn)生了相對運動，并帶動介于兩者之間的發(fā)電機往復(fù)轉(zhuǎn)動起來。因此，這臺波力發(fā)電機能在有波浪的海里不斷輸出波動的電能。

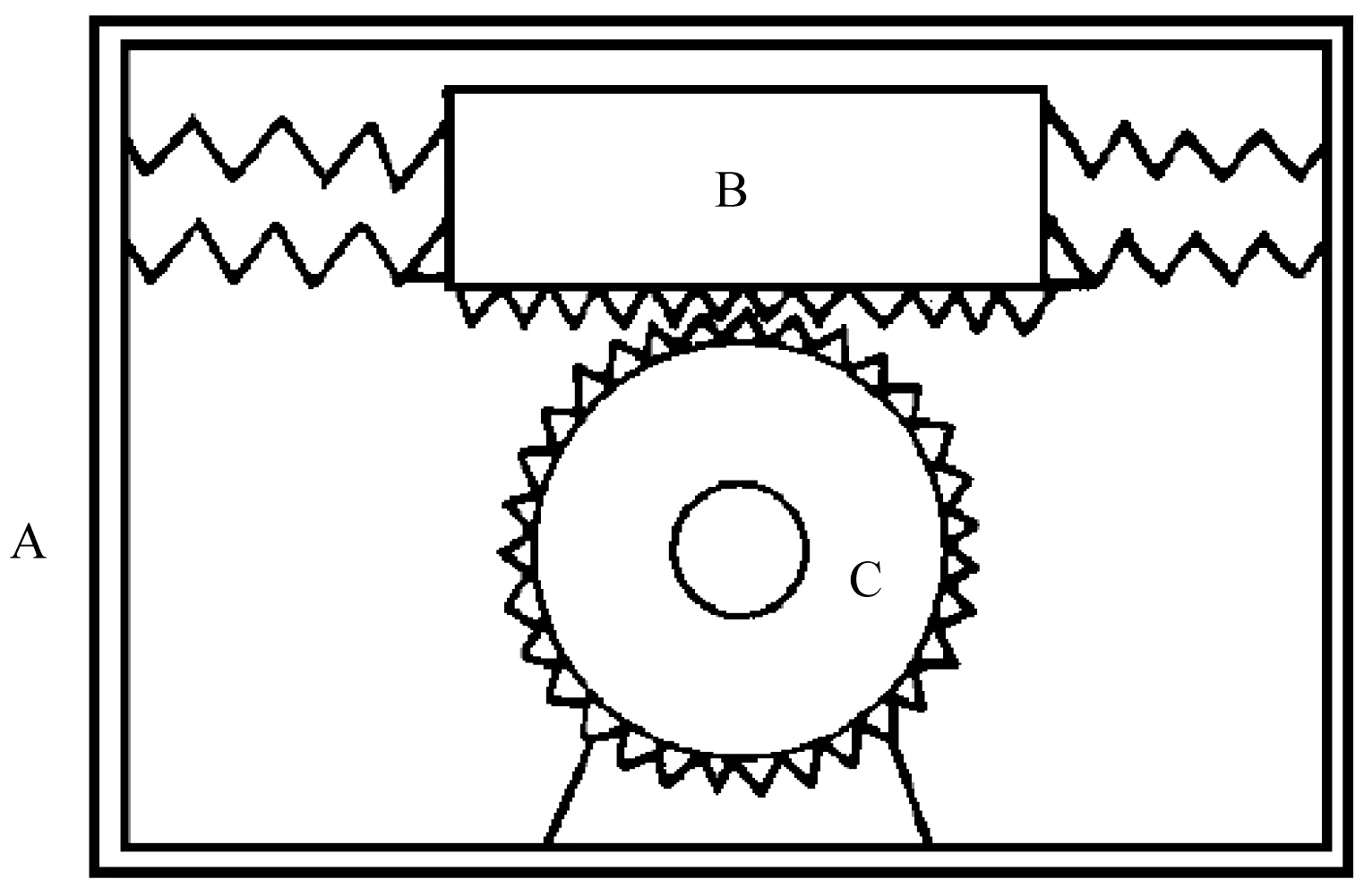
圖1 波力發(fā)電機原理圖Fig.1 Wave generator schematic diagram

帆船在航海時，遇到順風(fēng)就把帆張開乘風(fēng)前進，遇到逆風(fēng)就把帆扯下拋錨停下來，等到順風(fēng)重新來到。一根木頭在海上漂浮的時候同樣會遇到順風(fēng)和逆風(fēng)，由于木頭不能對不同風(fēng)向的作用力進行選擇，它只能在海上忽東忽西的夢游，很難向特定的目標(biāo)進發(fā)。和隨風(fēng)飄流的木頭不一樣，帆船的行為是一種目的性的形為。學(xué)術(shù)界通常認(rèn)為只有生物才能具有這種行為方式，要從物理學(xué)角度研究目的性行為，目前有進展但依然困難重重。

有種滑鎖裝置，它由一個彈簧閘和一個帶齒的圓柱組成，前者叫滑車，后者叫滑道，滑道的一個斜面大于摩擦角，另一個小于摩擦角，如圖2所示。

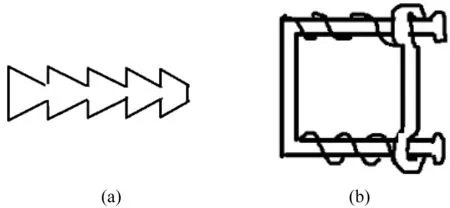
圖2 滑鎖裝置簡圖Fig.2 Sliding lock device diagram

把滑車套在滑道上，可以推動它沿滑道前進。但不能把它往后推，反向推動滑車就卡在滑道上了。這樣滑車只能沿滑道前進，不能后退。如果滑車小到一定程度就變成了一個“有理有智”的花粉，漲落力只能使它沿滑道前進，而不能使它后退和偏離滑道。這時在漲落力的作用下它的運動方式不是無規(guī)則的布朗運動，而是有規(guī)則的定向移動［30］。

滑車可以沿環(huán)狀滑道永遠(yuǎn)地單向轉(zhuǎn)動，也可以沿滑道爬升，如圖3。滑車爬升過程中漲落產(chǎn)生的負(fù)熵和自由能并不是重新消失了，而是以重力勢能的形式積累起來。本文只討論了控制一個滑車爬升的工作原理，但用同樣方法能使億萬個滑車進行同樣的工作，如并排修建多滑道，或者在每個滑道上串入多滑車，那么就能把大量漲落能轉(zhuǎn)換成重力勢能，使問題進入宏觀層次［31］。

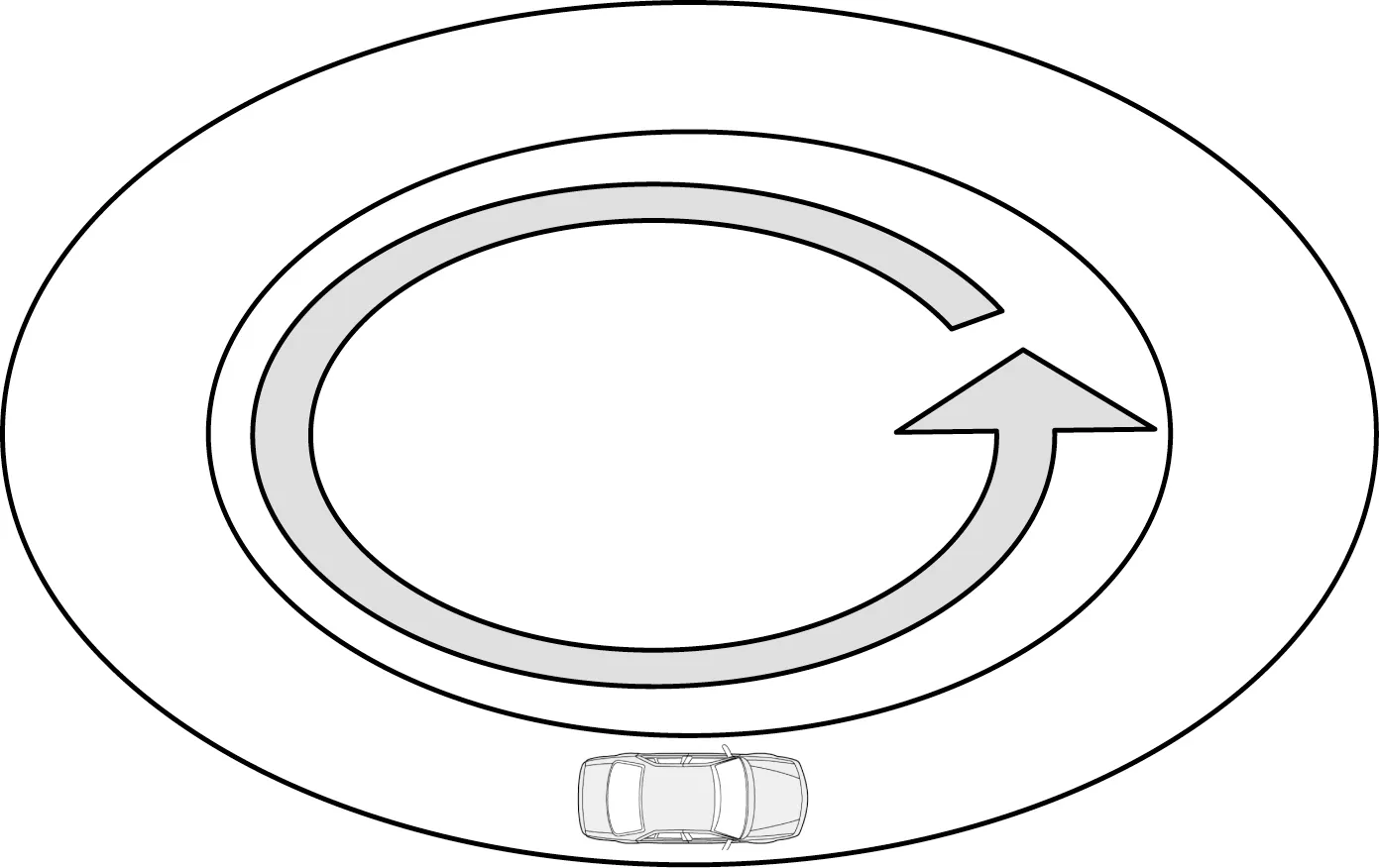
圖3 滑車示意圖Fig.3 Schematic diagram of pulley

3 結(jié)語

作為近平衡態(tài)統(tǒng)計物理最重要的理論之一，漲落耗散理論深刻揭示了平衡系統(tǒng)同時存在漲落、耗散這兩種根本現(xiàn)象之間的關(guān)聯(lián)，且在宏觀上通過平衡性質(zhì)表現(xiàn)非平衡性質(zhì)。在近平衡態(tài)熱力學(xué)統(tǒng)計物理中，漲落耗散理論與輸運系數(shù)對稱理論、最小熵理論之間都存在密切關(guān)系，且輸運系數(shù)對稱理論可根據(jù)漲落耗散定理與微觀可逆性導(dǎo)出，結(jié)合理論，對可能的應(yīng)用方向進行了探討。