多種隨機載荷下的風電設備動態可靠度分析
孫 逸,張西龍
(中國電建集團西北勘測設計研究院有限公司,陜西省西安市 710065)
0 引言
可靠度理論,一般是基于應力—強度干涉理論而建立的靜態分析理論[1]。然而在實際工況下,設備受到的載荷往往是多次且隨機的,并且設備在疲勞、老化等因素的影響下,其強度也必然會變化,因此,基于干涉理論的可靠性模型一般會造成不可忽視的誤差[2-3]。國內學者王正[4]運用統計學原理,建立隨機載荷多次作用下的等效分布函數,將隨機載荷的作用次數視為隨時間變化的量,由此提出了動態可靠度計算理論。
對于風電設備,由于其輸入載荷、材料狀態等均具有強烈的隨機性,可靠性模型往往處于非線性受力狀態。同濟大學李杰教授[5]及其團隊提出了一種適用于一般隨機系統,可以分析系統隨機信息的概率密度演化理論,在復雜多自由度結構系統分析方面取得了較為不錯的反響。本文結合王正提出的動態可靠度模型與李杰的概率密度演化法,提出一種新的動態可靠度計算方法,旨在獲得真實、有效且計算簡便的結果。
1 動態可靠度的概述
一般情況下,風電設備可靠性的設計與核驗多采用有限元建模方法,即對風電設備各個零件進行強度分析,繼而擴展至整個機組系統。該方法基于商業軟件的計算,是現在的主流分析手段[5]。但是,有限元建模方法往往只能對模型進行靜力、較短時間范疇的動力可靠度計算。這與實際情況下有著顯著的差異,風電機組往往承受著強風、地震等在空間、時間、強度維度上變化的隨機載荷。因此,單一地考慮風電設備在某時間節點、受到某一定量的載荷而求得的靜態可靠度,無法準確地計算長時間工作的風電設備壽命與可靠度,不具備普適性。
可靠度,作為工程領域中一個非常重要的指標,其對于產品設備的結構設計、維護修理、壽命預測有著不可代替的指導作用。因此,精確計算設備可靠性,從而保障人員生命安全、減少財產損失、節約生產成本的目的,是現代機械領域十分重要的研究方向。
可靠性,是定性指標,一般指設備在一定時間下,正常運轉的能力。而可靠度,則是數量指標,指設備在一定時間下,正常運轉的概率[6]。
假定某一設備零件所受載荷的應力S和自身的強度γ分別為服從相互獨立的某種隨機分布的概率函數,其概率密度函數分別為fS(S)、fγ(γ)。則可靠度可定義為:

如圖1所示為應力—強度干涉理論的示意圖。在同一坐標系下,當載荷S與零件強度γ分別服從某種分布時,二者的概率密度未重疊部分屬于絕對安全區,因為該區域內γ>S;載荷S與零件強度γ重疊部分,即圖中陰影為失效區,γ<S,稱之為應力S和強度γ的干涉區。顯然,當干涉區越小,意味著可靠度越大,零件越安全。
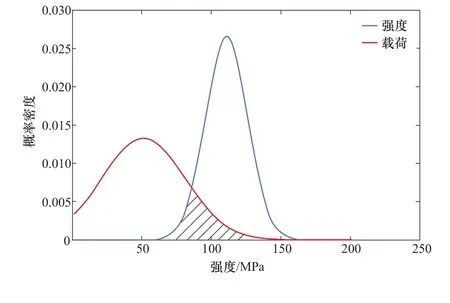
圖1 應力S和強度γ的干涉Figure 1 Interference between S and γ
由積分學可得,事件(γ>S)發生的概率,即可靠度為:

實際工作中,機械設備往往是在服役期內多次往復運作,若忽視應力作用次數及其帶來的疲勞磨損,將會導致模型計算與實際工程嚴重脫節。
由應力—強度干涉理論可得,載荷多次作用下的零件可靠度可通過如下積分式獲得:
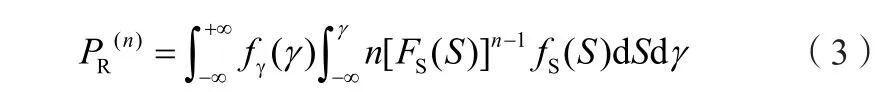
設在任意時刻t,載荷出現n次的概率服從參數為λ的分布:

其中,N(t)指在時刻t時載荷出現n次;P(n)為載荷出現n次的概率。
結合可靠度公式(3),零件在t時刻載荷作用n次時的可靠度為:
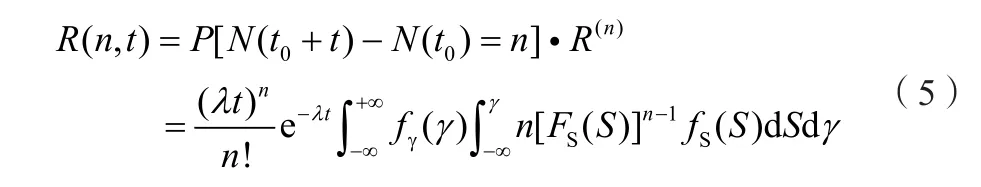
通過極限求和,可以最終得到零件在任意時刻下的動態可靠度:
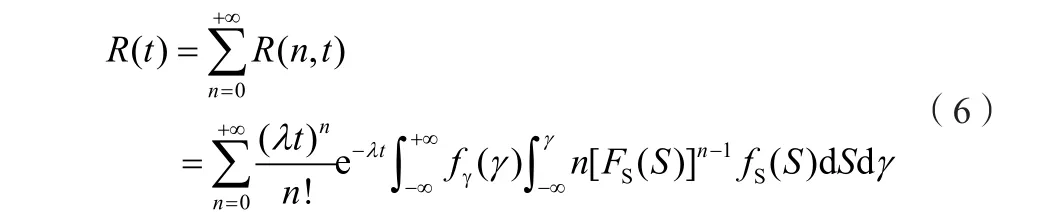
進一步對公式(6)中的指數部分進行泰勒展開,可以將其化簡為:
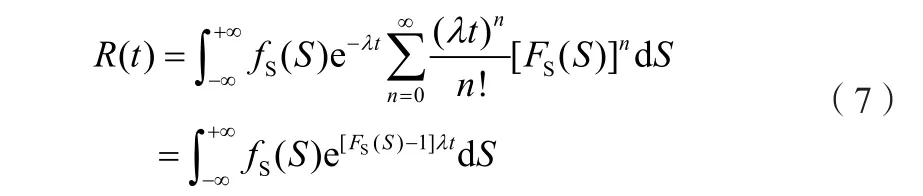
以上公式都是建立在零件自身的強度不變的基礎上進行。但在實際工程中,機械零件自身由于疲勞損傷、腐蝕老化等原因,其強度會發生退化。本文將零件強度的退化簡化為與時間有關的函數,對原強度分布進行加權處理。零件的強度取決于初始強度γ0與加權因子的共同影響。其公式如下:
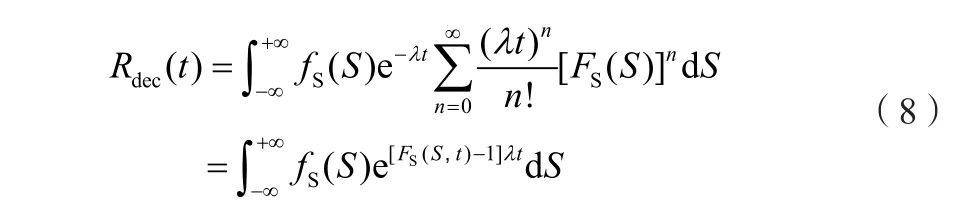
2 概率密度演化理論
上述動態可靠度模型,將靜態可靠度改良為載荷多次作用下的時變動態可靠度。但是,該模型僅僅將輸入載荷簡單地歸納為一個或多個同種的載荷,再進行簡單地疊加、相乘。事實上,風電機組的工況往往是復雜、多變的:無論是輸入載荷、零件自身狀況,其在時間、空間上的激勵均具有隨機性,導致結果是系統將以多個維度且非線性的形式輸出。若運用干涉模型進行積分,將會帶來巨大的計算量。而李杰教授[7]提出的概率密度演化法則很好地解決了這個問題,該理論的誕生就是為了解決土木工程中,強風、地震、海嘯等強隨機性輸入下的非線性動力系統問題。
記Z(t)為需要研究解決的最終結果,系統所有的隨機參數用同一函數表征,則有等式如下:
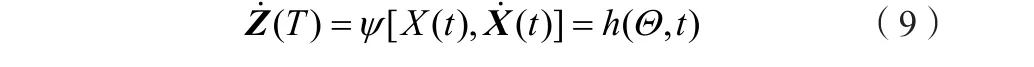
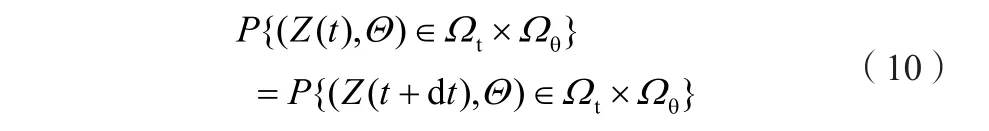
表達為積分形式,則為:
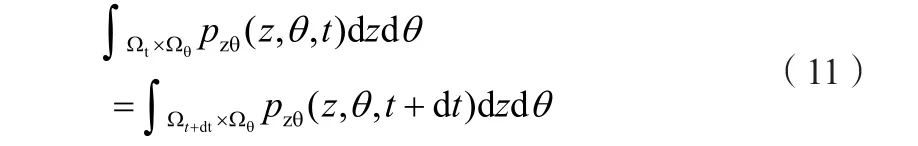
在微小時間增量dt之后的t+dt時刻,Ωt+dt是Ωt及其邊界運動疊加的結果,即:

由此可見,無論在任意時刻t≠t0,Ωt均依賴于Ωθ。這也是必須考慮增廣系統而非系統Z(t)的原因。
將式(12)代入式(11),先考慮等式的右側,有:
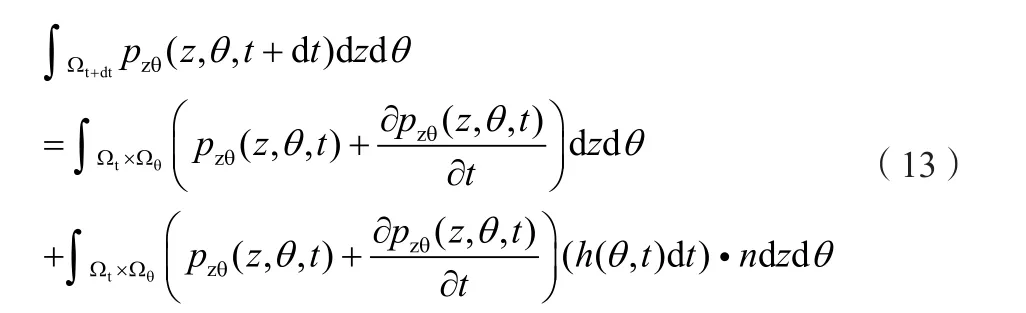
將式(13)代入式(11)右側,化簡可得:
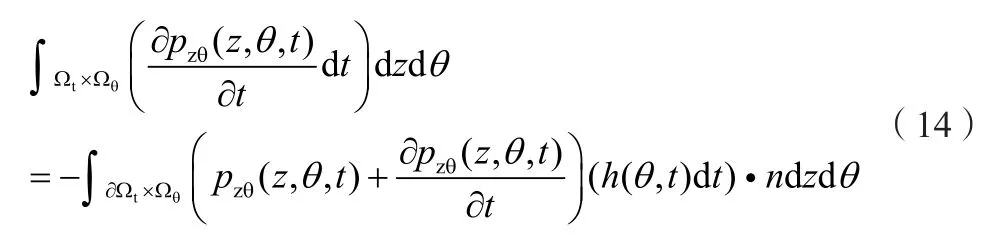
應用散度定理,并略去高階項,式(14)可記作:
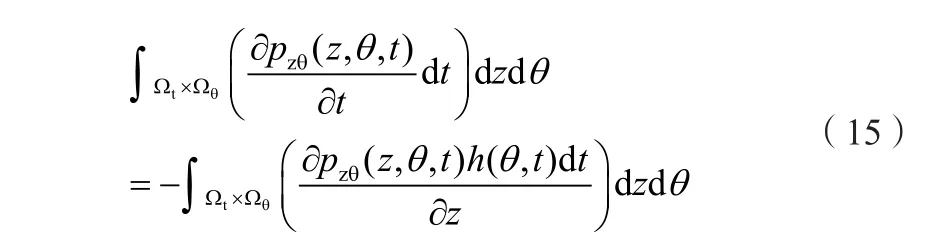
考慮到Ωt×Ωθ的任意性,并消去等式兩邊的dt,可最終得到概率密度演化方程:
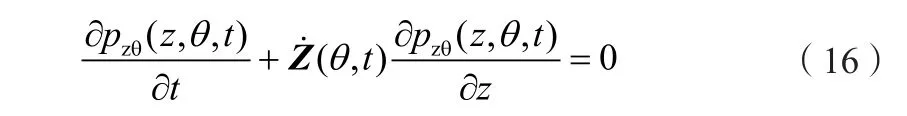
如圖2所示為不同時刻下典型概率密度演化函數。可以清楚地看到,隨著時間的演化,可靠度關于載荷強度的概率密度有著明顯的變化。隨著零件工作時長的增加,可靠度的概率密度會逐漸“扁平化”,說明該零件在更廣泛的載荷范圍內都有著失效的風險,即隨著零件工作時間的增加,其失效的可能性越大,這與我們的常識相符合。
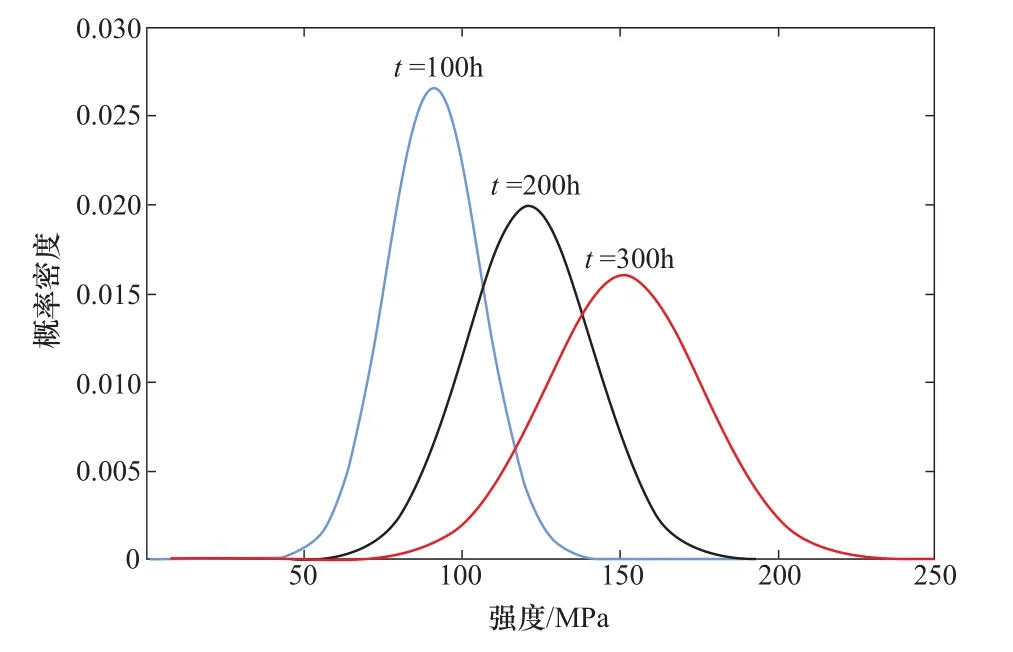
圖2 不同時刻下典型概率密度演化函數Figure 2 Evolution function of typical probability density at different time
3 概率密度演化理論下的動態可靠度
3.1 可靠度的數學模型
基于應力強度干涉理論的可靠度概率密度函數表達式為:
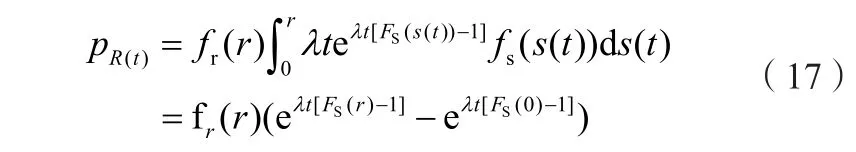
由于結構在服役過程中,不再有其他隨機載荷介入,此時整個系統處于概率守恒狀態,故pR(t)應滿足概率密度演方程:
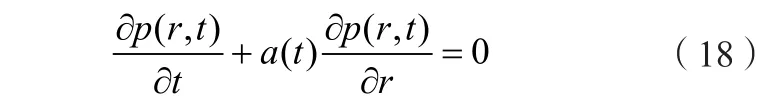
其中,a(t)為Dirac函數,它在除零以外的點上都等于零,且其在整個定義域上的積分等于1。
聯立式(18)與上述初始條件,可以求得動態可靠度的密度函數p(r,t)。而通過對該密度函數關于載荷定義域上的不定積分,可得最終的動態可靠度:

式(19)即為基于概率密度演化理論的零件動態可靠度的理論解析表達式。由方程(18)可知,該聯立方程的求解可以視為于解偏微分方程的初值問題。
若考慮零件強度隨時間退化,可將零件強度進行加權處理。一般零件強度退化模式有:線性退化、對數退化、指數退化。結合式(17)與強度退化函數,可得在退化條件下,多次隨機載荷下的可靠度概率密度函數表達式:

同式(18),其概率密度演方程為:
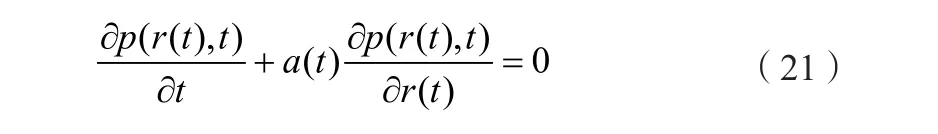
最終的動態可靠度Rdec(t)的表達式為:
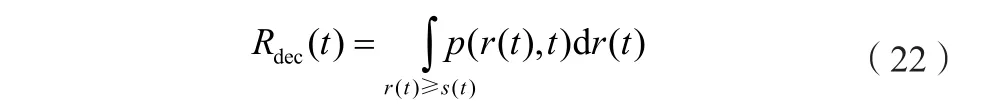
3.2 演化方程的數值計算
簡單的偏微分方程,一般的商業數學軟件就能滿足計算需要,但在面對存在巨大計算量的實際工程需要時,數值求解是現實而又必須的[8]。本文擬用數值分析中最常用的單邊差分格式有限差分法,來解決該問題。概率密度演化理論的數值計算可采用如圖3所示的流程。
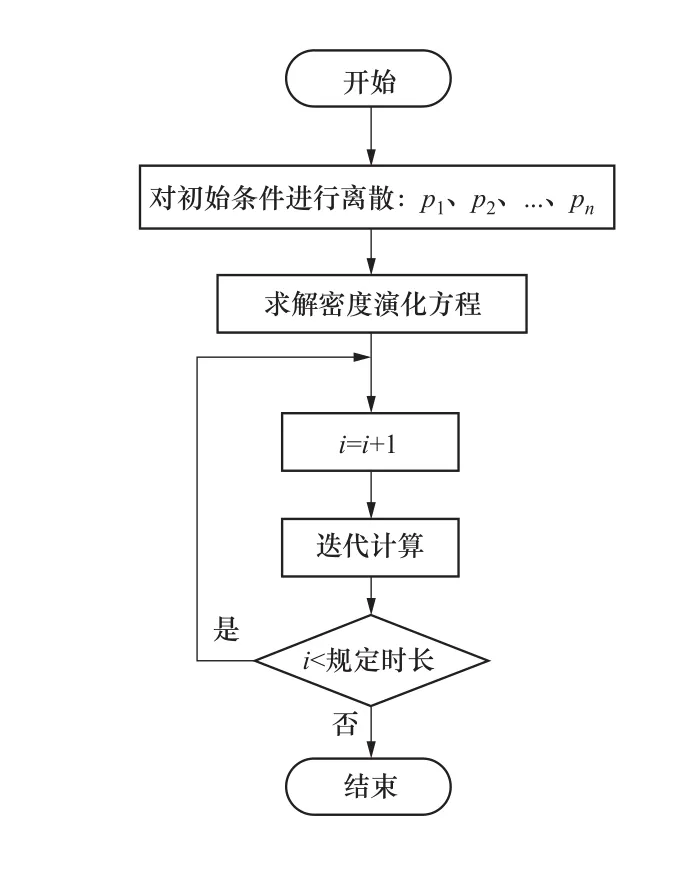
圖3 計算流程圖Figure 3 Calculation flow chart
如圖4所示,對求解域進行網絡劃分,即將r-t空間進行離散:rn= nΔr,ti=iΔt。u在點(n,i)的值為,根據微分的數學定義,可以近似得到的值為。同理,。因此,偏微分方程在點(nΔr,iΔt)處可近似為:
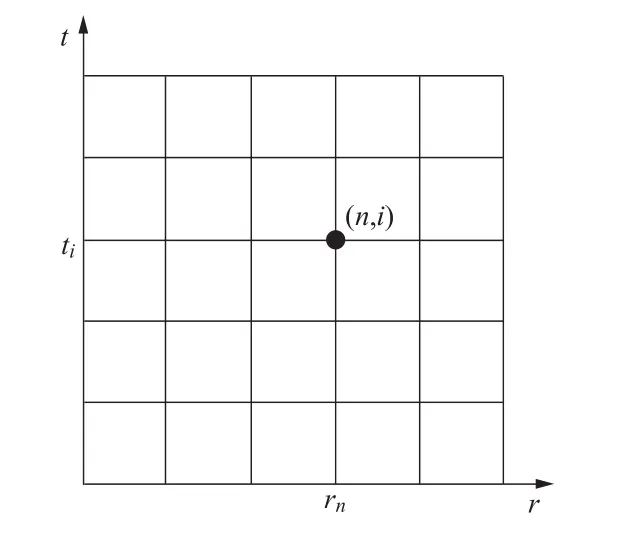
圖4 網絡劃分Figure 4 Network division
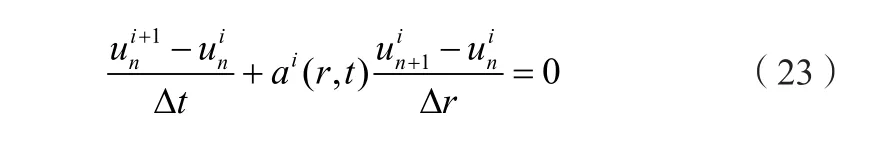
3.3 算例
某一零件強度服從均值為μr=300MPa、標準差為σr=30MPa的正態分布;載荷S服從均值為μs=200MPa、標準差為σs=40MPa的正態分布。在載荷多次作用時,取λ=1,va(t)=0.5,誤差不超過10-3。
根據式(22),求得的動態可靠度密度函數如圖5所示。
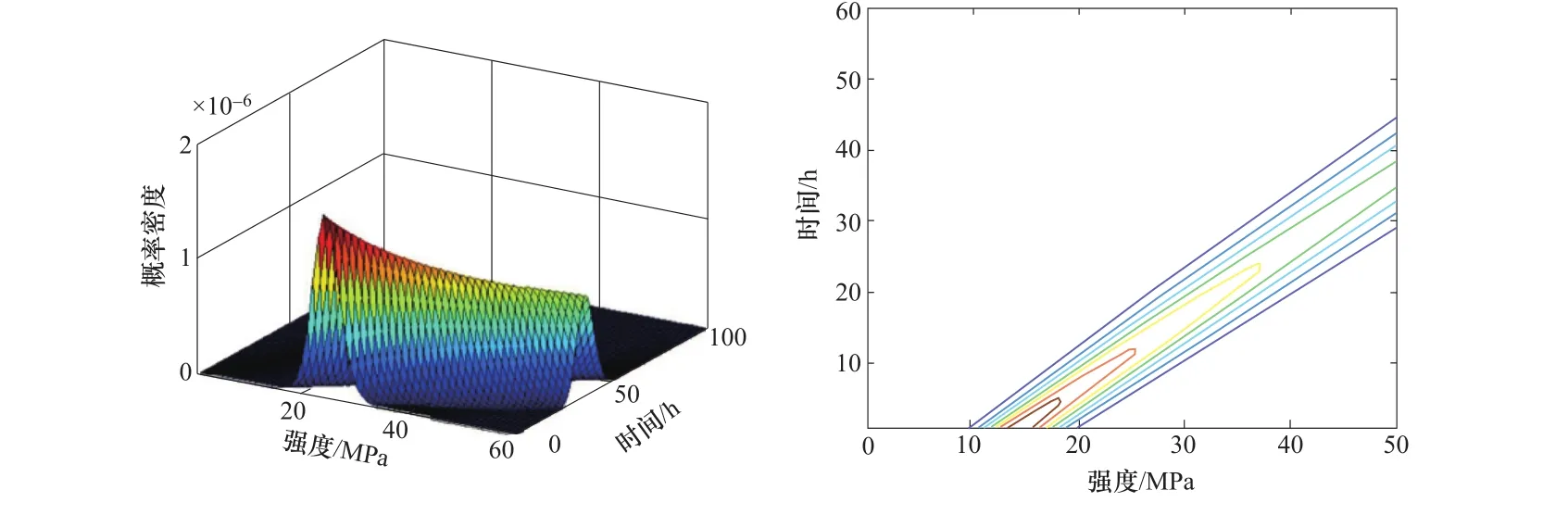
圖5 隨時間演化的概率密度函數Figure 5 Probability density function evolving with time
可以清晰看到,經由概率密度演化法計算的動態可靠度其概率密度會隨著時間的演化而扁平化,其函數圖峰值之間變低,在載荷強度定義域上逐漸分散。縱觀整個演化過程,其形如緩緩流動的河流;在三維視角上,則如連綿不斷又高低起伏的山脈。該現象為概率守恒的系統在狀態空間中流動演化的結果。回歸到零件可靠度的問題是,可以解讀為隨著零件工作的運作,可靠度的密度函數在載荷域上的分布逐漸變寬,致使零件失效的載荷域漸漸變大,零件失效的可能性在不斷提高。
如圖6、表1所示,為利用概率密度演化法計算得到的動態可靠度,與前文的動態可靠度和蒙特卡羅法模擬10000次的對比。可見,用本文方法求得的可靠度,仍保留了失效規律的“盆浴曲線”,并且比應力—強度干涉理論的結果更好地擬合了蒙特卡洛模擬結果[9]。由圖可知,構件磨合期結束后,零件的主要失效形式由磨損失效變為疲勞失效,構件的失效率會顯著降低,可靠度下降趨勢則逐漸變緩。當構件工作時長超過其額定工作時長后,零件的主要失效形式又由疲勞失效變為磨損失效,失效率顯著上升,可靠度下降趨勢隨之增大。利用概率密度演化法求得的動態可靠度,在構件進入疲勞失效期后,存在“磨損—疲勞”狀態改變的階變時間點,可靠度下降趨勢變化更加明顯,說明本文方法在描述構件動態可靠度的狀態改變方面更為準確。分別利用PDEM和干涉理論計算出的結果,與蒙特卡洛法做對比散點圖,如圖7所示。顯然,相比較干涉理論,PDEM計算的動態可靠度可以更好地擬合蒙特卡洛模擬結果,這足以說明密度演化模型的準確性。
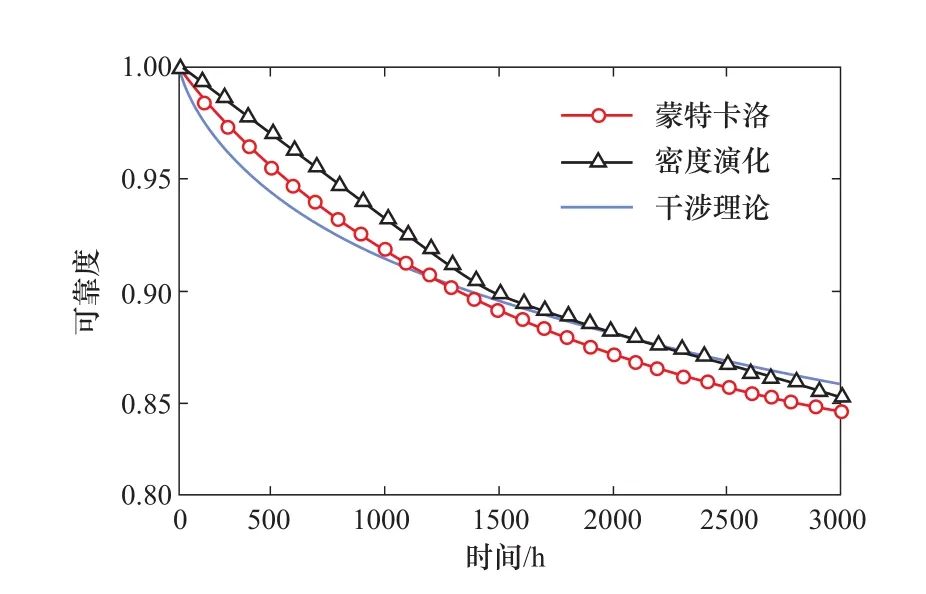
圖6 零件的動態可靠度Figure 6 Dynamic reliability of parts
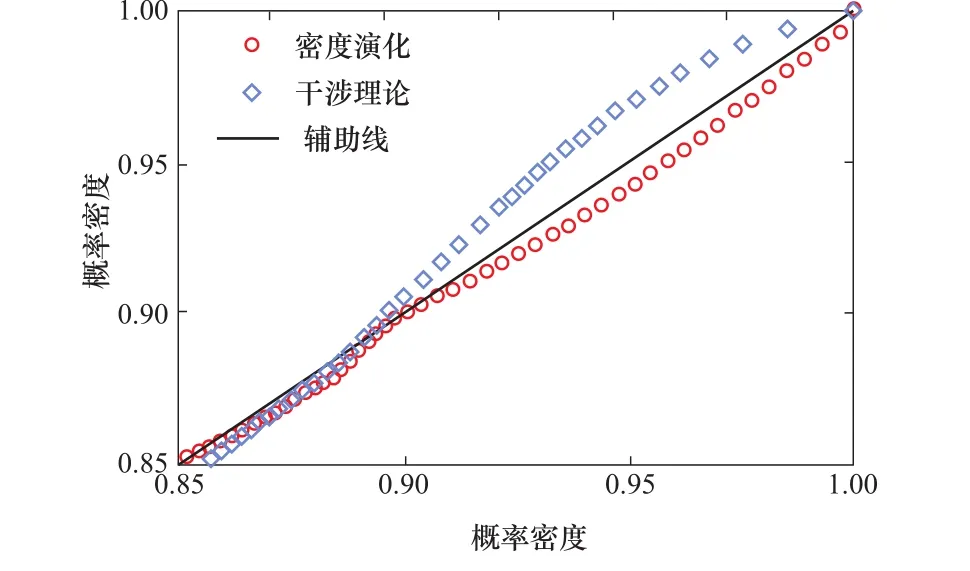
圖7 散點圖Figure 7 Scatter chart
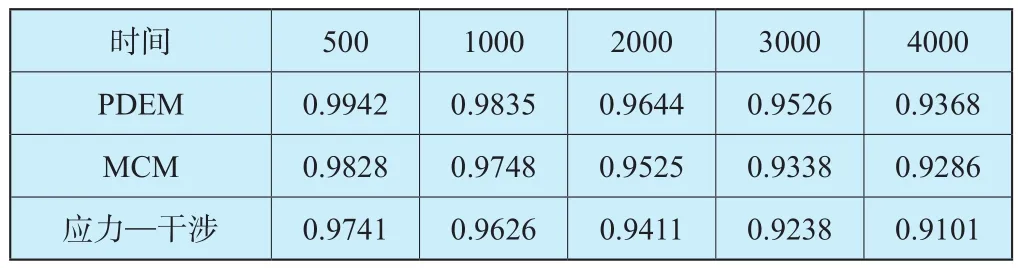
表1 不同時刻下單一零件的動態可靠度Table 1 Dynamic reliability of a single part at different times
若考慮零件為強度隨時間退化,其退化因子為μ(t)=1-0.00004t的線性函數,則圖8為退化條件下單一零件的動態可靠度,其中紅色為強度退化,黑色為強度不退化的對照組。表2為兩種條件下可靠度的數值記錄。
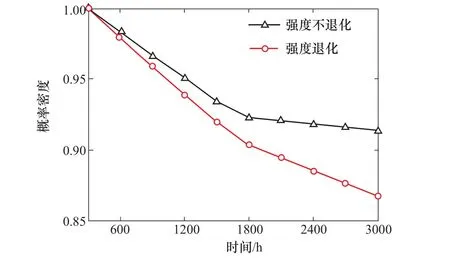
圖8 退化條件下單一零件的動態可靠度Figure 8 Dynamic reliability of single part under degradation condition

表2 不同時刻強度退化零件的動態可靠度Table 2 Dynamic reliability of parts with strength degradation at different times
4 結論
風電設備的可靠度計算,多采用有限元建模的方式。該方法較為準確、直觀,但由于有限元方法只能計算短時間內的結果,無法預測其長時間的狀態或可靠度。這顯然對于價值高、運轉時間長的風電設備是不利的。本文結合應力—強度干涉理論與概率密度演化方法,提出了一種可以考慮多種隨機輸入載荷,預測設備實時可靠度的數學模型。通過與仿真數據與Monte Carlo模擬數據對比,該方法可以有效預測設備的壽命及可靠性,可以為有限元建模與工程實際提供必要的輔助作用。

