基于改進(jìn)快速冪次趨近律的PMSM無(wú)速度傳感器控制

鄧 超，王 英

(大連交通大學(xué) 電氣信息工程學(xué)院，大連 116021)

0 引 言

永磁同步電機(jī)(以下簡(jiǎn)稱PMSM)由于其結(jié)構(gòu)簡(jiǎn)單、功率因數(shù)高、起動(dòng)轉(zhuǎn)矩大等優(yōu)點(diǎn)，在工業(yè)、交通以及國(guó)防等領(lǐng)域得到越來(lái)越廣泛的應(yīng)用[1-2]。

PMSM調(diào)速系統(tǒng)的性能與控制算法密切相關(guān)，滑模控制是提高系統(tǒng)性能的一個(gè)重要方法，系統(tǒng)采用滑模控制可以提高系統(tǒng)的響應(yīng)速度、增強(qiáng)系統(tǒng)的魯棒性，但由于其控制的不連續(xù)性，在滑模面附近做高頻切換運(yùn)動(dòng)會(huì)產(chǎn)生抖振問(wèn)題。為了抑制滑模的抖振，文獻(xiàn)[3]提出了一種基于傳統(tǒng)指數(shù)趨近律滑模控制的自適應(yīng)漸消擴(kuò)展卡爾曼濾波(AFEKF)控制系統(tǒng)，并在此基礎(chǔ)上對(duì)趨近律進(jìn)行了改進(jìn),得到的新型指數(shù)趨近律使抖振的變速項(xiàng)系數(shù)為零，抑制了抖振現(xiàn)象；文獻(xiàn)[4]討論了根據(jù)不同的系統(tǒng)狀態(tài)來(lái)對(duì)雙冪次趨近律中冪次項(xiàng)系數(shù)進(jìn)行調(diào)節(jié)以提升系統(tǒng)狀態(tài)逼近滑模面附近的動(dòng)態(tài)品質(zhì)；文獻(xiàn)[5]討論了雙冪次趨近律的滑模控制收斂時(shí)間與滑模初始狀態(tài)的關(guān)系，指出雙冪次趨近律的特定時(shí)間收斂的特點(diǎn)；文獻(xiàn)[6]提出了一種基于雙曲正切函數(shù)的改進(jìn)型PMSM無(wú)感矢量控制系統(tǒng)，推導(dǎo)了基于雙曲正切函數(shù)的滑模觀測(cè)器轉(zhuǎn)子位置估算算法。

本文對(duì)基于擴(kuò)展卡爾曼濾波(以下簡(jiǎn)稱EKF)的PMSM無(wú)速度傳感器控制系統(tǒng)速度環(huán)進(jìn)行了研究，設(shè)計(jì)了一種快速冪次趨近律改進(jìn)控制算法，在快速冪次趨近律的冪次項(xiàng)上加入了可以自適應(yīng)調(diào)節(jié)的冪次項(xiàng)系數(shù)，在加快趨近速度的同時(shí)，保留了冪次項(xiàng)的優(yōu)點(diǎn)，同時(shí)將趨近律中的開(kāi)關(guān)函數(shù)由雙曲正切函數(shù)替換，雙曲正切函數(shù)相比于不連續(xù)的開(kāi)關(guān)函數(shù)，其變化平緩，不存在突變，在一定程度上削弱了滑模運(yùn)行過(guò)程中的抖振。仿真分析表明，改進(jìn)型趨近律起動(dòng)過(guò)程更加平穩(wěn)，轉(zhuǎn)速跟蹤波形收斂速度更快且抑制了抖振。

1 基于EKF的PMSM無(wú)速度傳感器控制系統(tǒng)

圖1為基于EKF的PMSM無(wú)速度傳感器控制系統(tǒng)結(jié)構(gòu)圖。

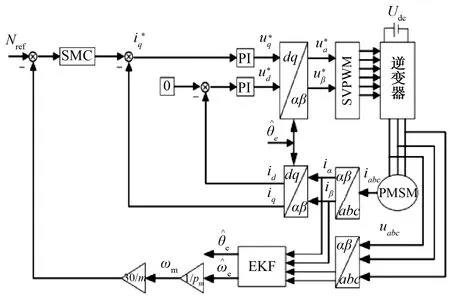
圖1 基于EKF的無(wú)速度傳感器控制系統(tǒng)結(jié)構(gòu)圖

PMSM 矢量控制為典型的閉環(huán)控制系統(tǒng)，其中包括內(nèi)部電流閉環(huán)與外部轉(zhuǎn)速閉環(huán)，外環(huán)EKF估算模塊的輸入為PMSM的參考電壓和電流值，輸出為估算的轉(zhuǎn)子位置信息以及轉(zhuǎn)速信息。EKF的算法主要可分為兩步，首先為對(duì)狀態(tài)矢量的預(yù)測(cè)階段，其次為對(duì)預(yù)測(cè)值的校正階段。

預(yù)測(cè)階段分為如下4步：

(1)

(2)

(3)對(duì)誤差協(xié)方差矩陣進(jìn)行計(jì)算：

(3)

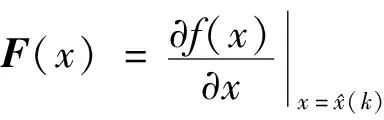
(4)

(4)計(jì)算增益矩陣K(k+1)：

(5)

校正階段分為如下2步：

(6)

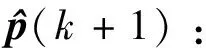
(7)

同時(shí)針對(duì)EKF初始協(xié)方差矩陣及其初值選擇如下：

式中：Q為系統(tǒng)噪聲協(xié)方差矩陣；R為測(cè)量噪聲協(xié)方差矩陣；P0為初值矩陣。

在本系統(tǒng)中，采用id=0轉(zhuǎn)子磁場(chǎng)定向的控制策略，轉(zhuǎn)速外環(huán)使用了滑模速度控制器，趨近律選擇使用了快速冪次趨近律[7]，其表達(dá)式如下：

(8)

式中：k1>0，k2>0，0<ε<1。

2 改進(jìn)型快速冪次趨近律

為了進(jìn)一步提高系統(tǒng)狀態(tài)變量的運(yùn)動(dòng)品質(zhì)以及更好地抑制抖振，本文在快速冪次趨近律式(8)的基礎(chǔ)上設(shè)計(jì)了一種改進(jìn)型趨近律，其表達(dá)式如下：

(9)

式中：k1>0，k2>0，ε→0+。

依據(jù)滑模控制的基本原理，為了保證系統(tǒng)狀態(tài)空間變量能夠從任意不確定的初始狀態(tài)在規(guī)定時(shí)間內(nèi)達(dá)到滑模面，需要滿足滑動(dòng)模態(tài)的可達(dá)性條件，其關(guān)系式如下：

(10)

對(duì)改進(jìn)型趨近律進(jìn)行穩(wěn)定性判定，驗(yàn)證該趨近律滿足Lyapunov穩(wěn)定性。

選取Lyapunov函數(shù)：

(11)

對(duì)式(11)求導(dǎo)可得：

(12)

由式(12)可得該改進(jìn)型趨近律滿足Lyapunov穩(wěn)定性判定，表明在該趨近律作用下，控制系統(tǒng)是逐漸穩(wěn)定的。

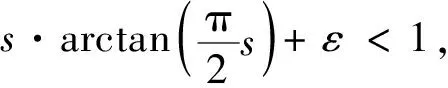
改進(jìn)型趨近律函數(shù)項(xiàng)采用雙曲正切函數(shù)tanh(s)代替開(kāi)關(guān)函數(shù)sgn(s)，其函數(shù)圖象對(duì)比如圖2所示。從圖2中可以看出，雙曲正切函數(shù)變化平緩，不存在突變，使得滑模控制器的控制效果更好，系統(tǒng)狀態(tài)更穩(wěn)定，能夠在一定程度上抑制抖振現(xiàn)象，減小抖振。

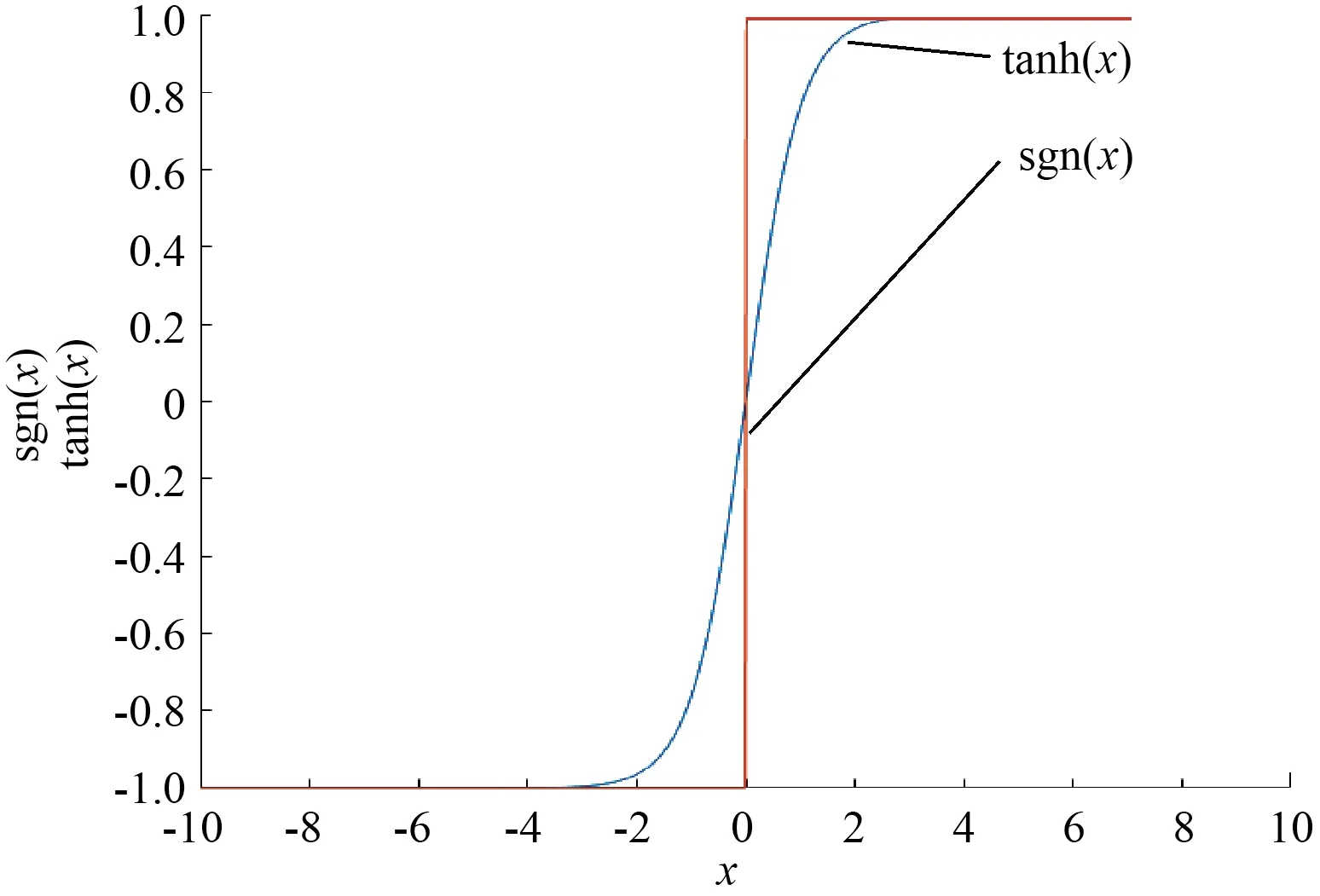
圖2 雙曲正切函數(shù)圖與開(kāi)關(guān)函數(shù)圖

3 滑模速度控制器設(shè)計(jì)

為了便于滑模速度控制器的設(shè)計(jì)，驗(yàn)證改進(jìn)型趨近律的控制效果，本文以表貼式三相PMSM為控制對(duì)象，建立d-q坐標(biāo)系下的PMSM數(shù)學(xué)模型：

(13)

電磁轉(zhuǎn)矩方程及運(yùn)動(dòng)方程：

(14)

式(13)與式(14)中，ud，uq為d，q軸電壓；id，iq為d，q軸電流；Te為電磁轉(zhuǎn)矩；TL為負(fù)載轉(zhuǎn)矩；ωr為機(jī)械轉(zhuǎn)速；p為極對(duì)數(shù)。

對(duì)于表貼式PMSM來(lái)說(shuō)，采用id=0的轉(zhuǎn)子磁場(chǎng)定向控制可取得較好的控制效果，將式(13)與式(14)結(jié)合可得到如下數(shù)學(xué)模型：

(15)

對(duì)系統(tǒng)狀態(tài)變量進(jìn)行定義：

(16)

式中：ωref為電機(jī)的給定機(jī)械角速度。將式(16)與式(15)、式(14)結(jié)合可得到：

(17)

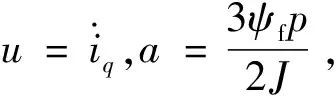
(18)

對(duì)滑模面函數(shù)進(jìn)行定義：

s=cx1+x2

(19)

對(duì)式(19)求導(dǎo)，即對(duì)滑模面求導(dǎo)可得：

(20)

進(jìn)而將本文提出的改進(jìn)型趨近律即式(9)與式(20)結(jié)合可得到：

(21)

由式(21)可得到iq表達(dá)式：

(22)

根據(jù)iq的表達(dá)式即可在Simulink中搭建滑模速度控制器。

4 仿真結(jié)果分析

為了驗(yàn)證改進(jìn)型趨近律的快速性與改善抖振的效果，基于MATLAB/Simulink搭建了如圖3所示的仿真模型。PMSM參數(shù)：Rs=2.625 Ω,Ls=0.008 6 H,p=4，ψf=0.173 Wb，J=0.006 kg·m2，預(yù)定轉(zhuǎn)速為500 r/min，初始時(shí)刻負(fù)載轉(zhuǎn)矩TL=0，仿真時(shí)間為2 s，在相同條件下，分別對(duì)基于快速冪次趨近律滑模控制和基于改進(jìn)型趨近律滑模控制的無(wú)速度傳感器控制系統(tǒng)進(jìn)行仿真，其轉(zhuǎn)速跟蹤波形如圖4、圖5所示。

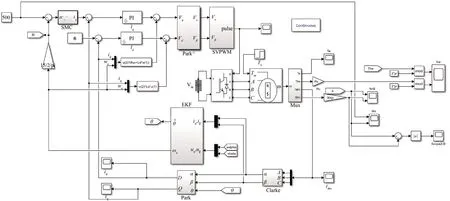
圖3 基于改進(jìn)型趨近率滑模控制的EKF無(wú)速度傳感器系統(tǒng)

由圖4和圖5的比較可以看出，在相同的條件下，當(dāng)電機(jī)由靜止起動(dòng)到達(dá)預(yù)定轉(zhuǎn)速的過(guò)程中，采用改進(jìn)型趨近律的無(wú)速度控制系統(tǒng)轉(zhuǎn)速跟蹤波形能夠更快地收斂到預(yù)定轉(zhuǎn)速，收斂時(shí)間由0.226 s減小到了0.143 s，收斂時(shí)間縮短了0.086 s，收斂速度提高了36%，表明改進(jìn)型趨近律相比于快速冪次趨近律而言，可以加快轉(zhuǎn)速跟蹤波形的收斂速度，驗(yàn)證了該趨近律的快速性。

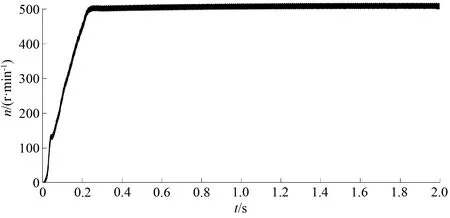
圖4 快速冪次趨近律滑模控制的EKF轉(zhuǎn)速跟蹤曲線

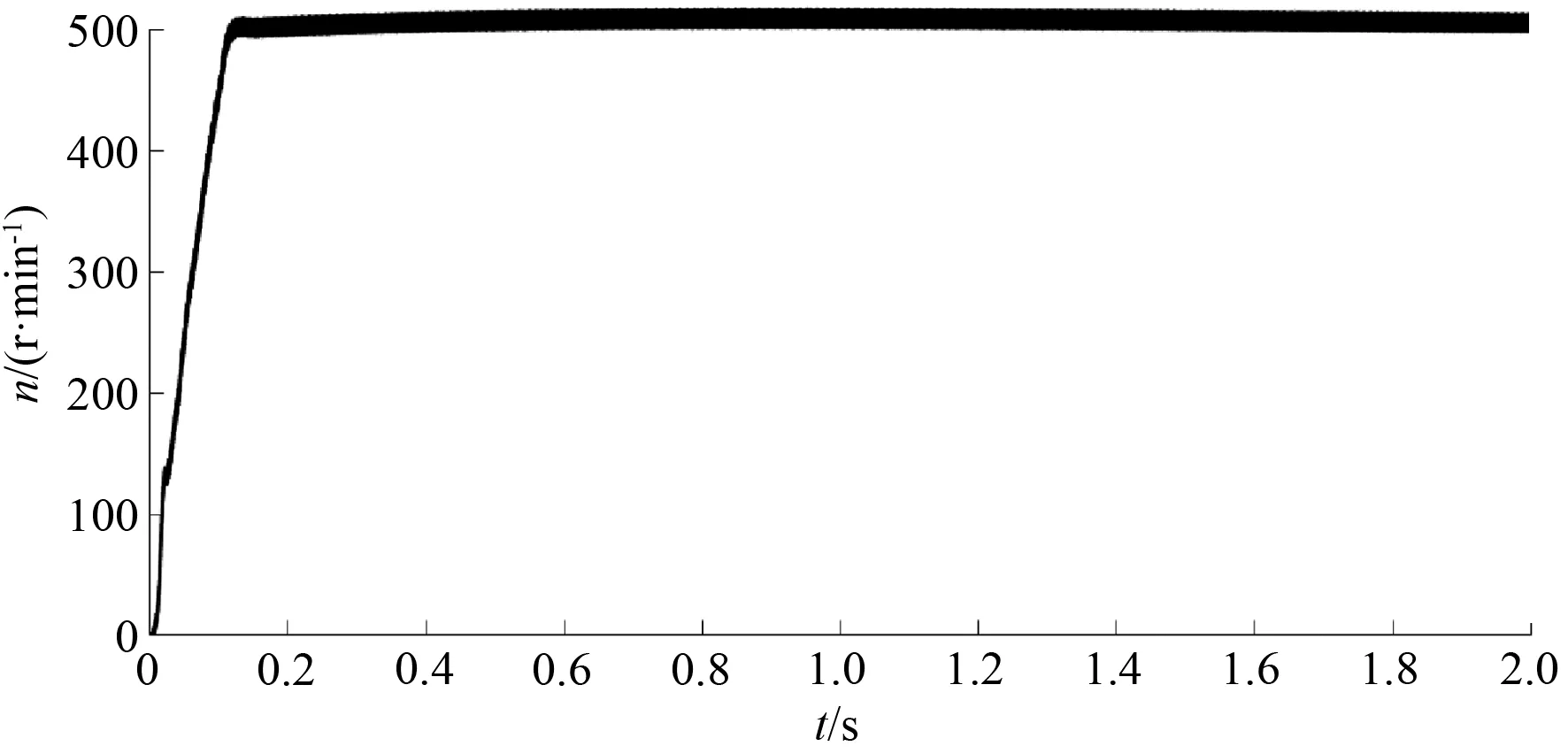
圖5 改進(jìn)型趨近律滑模控制的EKF轉(zhuǎn)速跟蹤曲線

圖6為改進(jìn)型趨近律的無(wú)速度控制系統(tǒng)對(duì)轉(zhuǎn)子位置的跟蹤圖。可以看出，轉(zhuǎn)子位置的實(shí)際值與轉(zhuǎn)子位置的估計(jì)值幾乎重合，實(shí)現(xiàn)了較好的跟蹤效果。

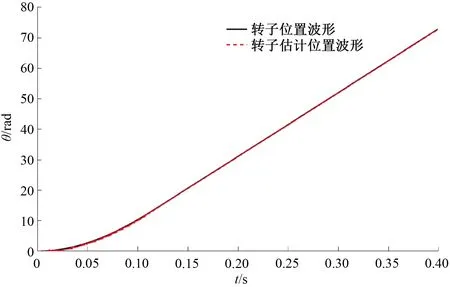
圖6 改進(jìn)型趨近律滑模控制的轉(zhuǎn)子位置跟蹤圖

圖7、圖8為轉(zhuǎn)速跟蹤波形局部放大圖。可以看出，在截取的相同時(shí)間內(nèi)，基于改進(jìn)型趨近律的無(wú)速度控制系統(tǒng)穩(wěn)態(tài)運(yùn)行時(shí)，轉(zhuǎn)速跟蹤波形抖振現(xiàn)象得到緩解，驗(yàn)證了改進(jìn)型趨近律函數(shù)項(xiàng)采用雙曲正切函數(shù)相比于開(kāi)關(guān)函數(shù)而言，能夠緩解轉(zhuǎn)速跟蹤波形的抖振，使得跟蹤波形更加穩(wěn)定。

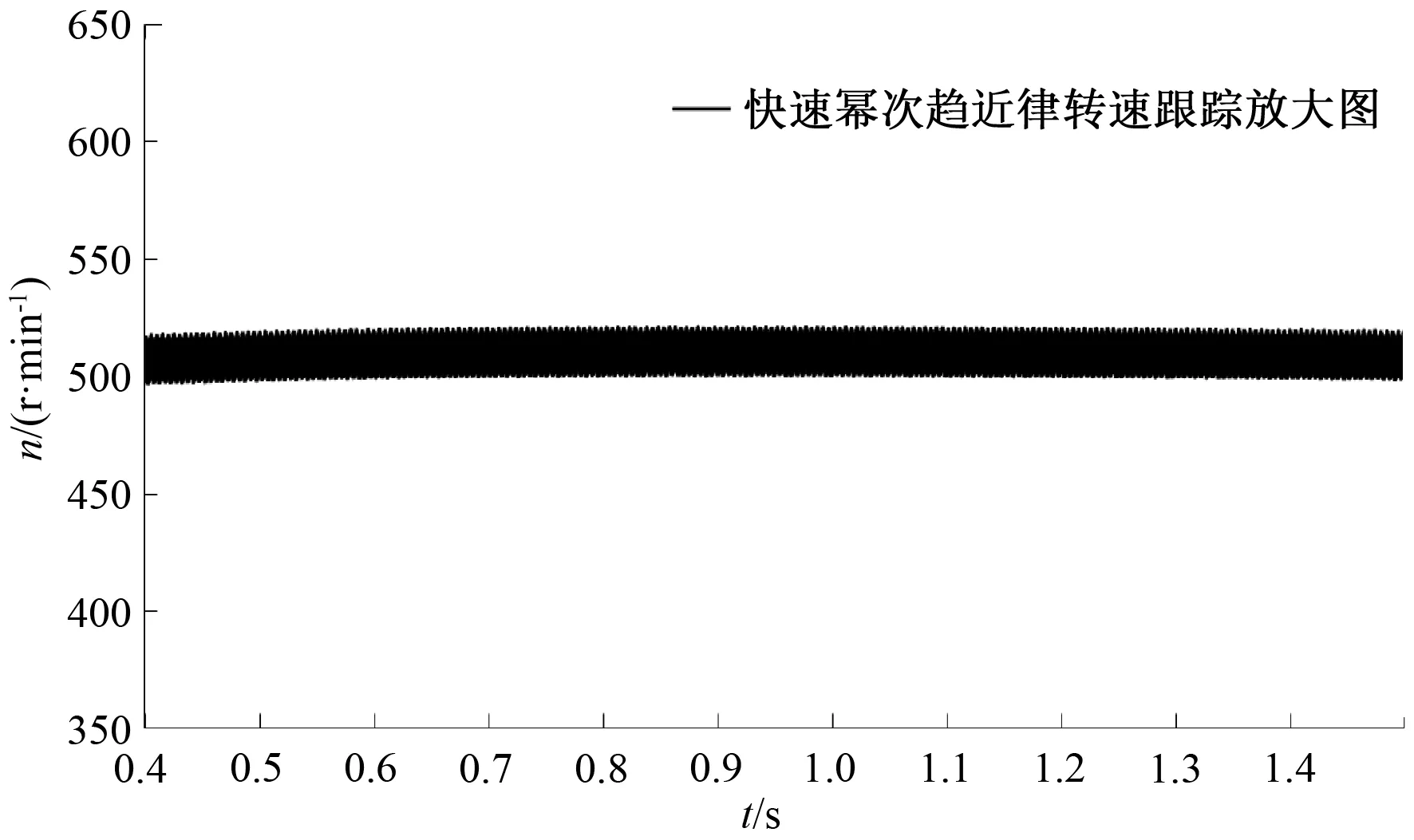
圖7 快速冪次趨近律滑模控制的轉(zhuǎn)速跟蹤放大圖

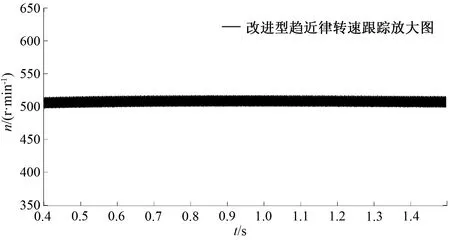
圖8 改進(jìn)型趨近律滑模控制的轉(zhuǎn)速跟蹤放大圖

5 結(jié) 語(yǔ)

本文為了加快滑模控制的趨近速度和改善抖振，設(shè)計(jì)了一種基于改進(jìn)型趨近律的滑模速度控制器，并通過(guò)仿真驗(yàn)證了改進(jìn)型趨近律趨近速度的快速性以及對(duì)抖振的抑制能力，使得應(yīng)用改進(jìn)型趨近律滑模控制的EKF無(wú)速度控制系統(tǒng)能夠滿足實(shí)際控制性能的需求。