基于AdvantEdge FEM的薄壁外殼體零件仿真分析

楊英歌，程會民，趙澤輝，韓文進，李云鵬

(西安北方光電科技防務有限公司，陜西 西安 710043)

圖1所示外殼體零件是某導引頭產品中最大的回轉體零件，零件材料為2A12-T4，外形尺寸為φ180 mm×277.5 mm。零件壁厚1.5～2 mm，一處關重特性要求，同軸度0.05 mm，垂直度0.05 mm，尺寸公差IT6～IT10。零件前端φ134H8 mm孔與整流罩相連，由于零件整體為光滑的圓柱與球形曲面相連接，使零件加工壓緊困難，難以實施基準孔、球形曲面及前端φ134H8 mm孔的加工。擬定的加工流程簡要如下：下料→車→熱處理→車→熱處理→數控車→數控車→熱處理→數控車→數控車→坐標鏜→鉗→檢驗→電加工→精飾→裝配。

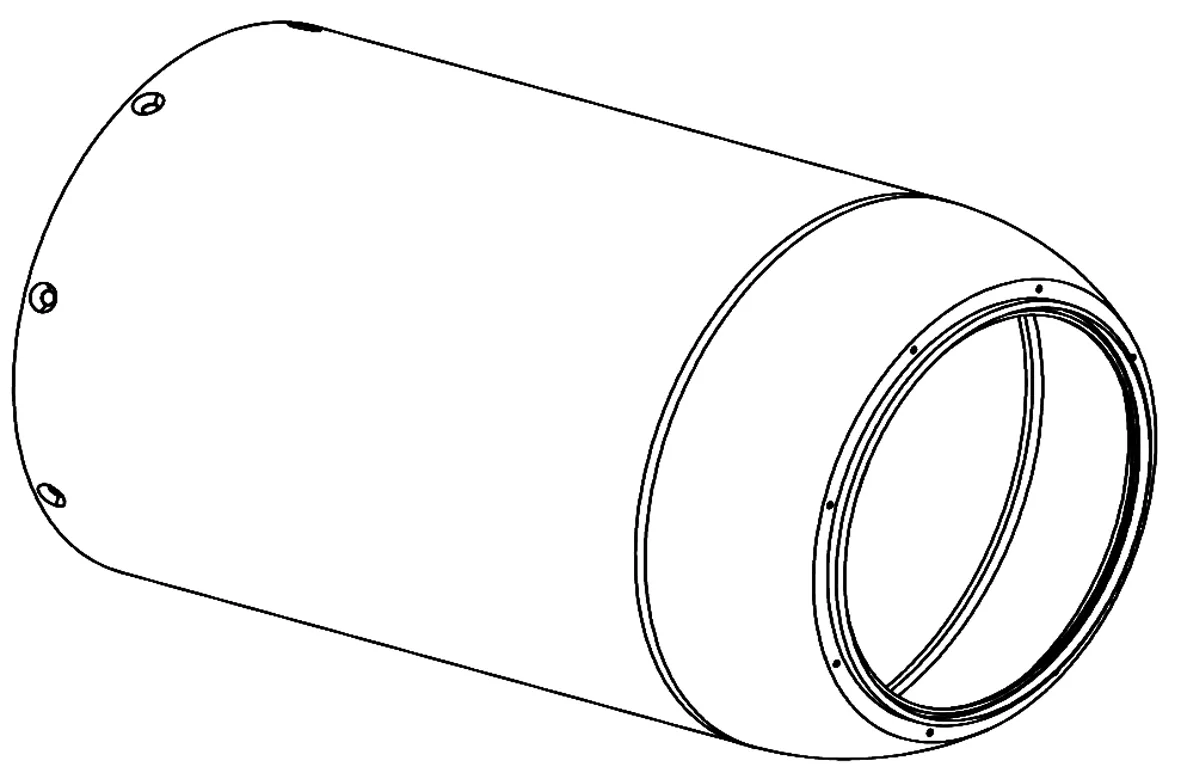
圖1 外殼體零件

該薄壁零件在數控車削加工過程中極易引起橢圓變形，其中包括裝夾帶來的壓緊力變形和切削過程中的切削力變形[1-3]。為盡量減小裝夾變形，在裝夾過程中使用力矩扳手，嚴格控制壓緊力。因此，該薄壁件變形的主要因素則主要考慮切削變形。合理的切削加工參數可提高切削效率和加工表面質量，并能夠降低切削力、切削溫度，使零件變形得到有效控制。本文借助有限元分析軟件，通過模擬薄壁外殼體件切削加工過程對其溫度場及應力場進行分析，并結合模態及諧響應分析，對切削參數進行優化。

1 建立薄壁外殼體件簡化模型

面向有限元仿真的外殼體結構件直接分析計算數據量巨大，不利于仿真分析計算。為進一步提高仿真效率，把握仿真總體趨勢，有必要對其進行結構簡化。對簡化模型切削加工過程進行有限元仿真，根據切削力及切削熱的變化趨勢對切削參數進行調整。

簡化的過程基于如下2點考慮：1)微小特征不利于對變形的總體結構分析，同時不能兼顧仿真效率和效果的統一，因此，在仿真分析中可以忽略孔、倒角等微小特征的影響將模型簡化；2)實際模型尺寸不利于仿真計算的效率提高，因此，在仿真分析中將模型縮小僅截取切削部分[4]。

2 薄壁外殼體結構件切削力仿真

切削條件：零件材料(2A12-T4)、刀片材料(硬質合金)、刀尖角(35°)、刀片前角(10°)、刀片后角(7°)、溫度(26 ℃)[5]，對3個變量(切削深度、每轉進給量、主軸轉速)進行3組仿真(試驗表分別見表1～表3)，分析各個變量對應力場、溫度場、第四強度應力場及塑性應變率的影響。

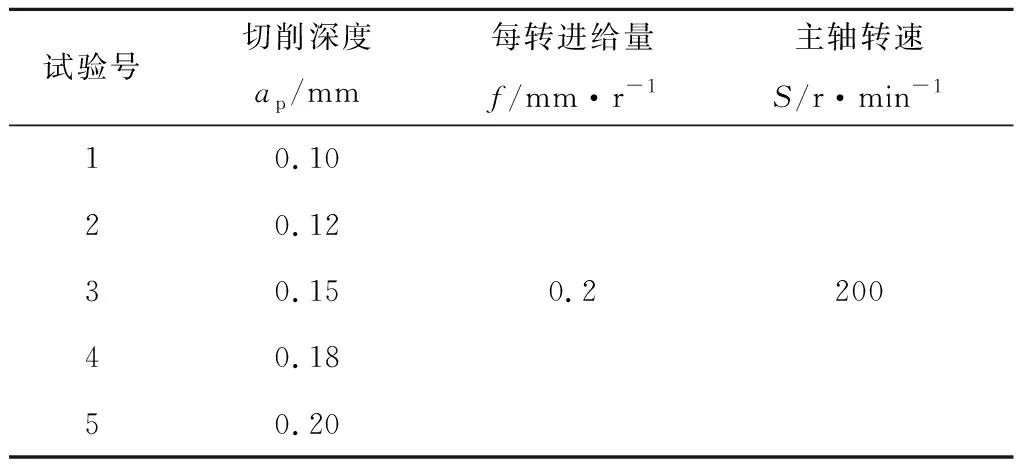
表1 切削深度影響試驗表

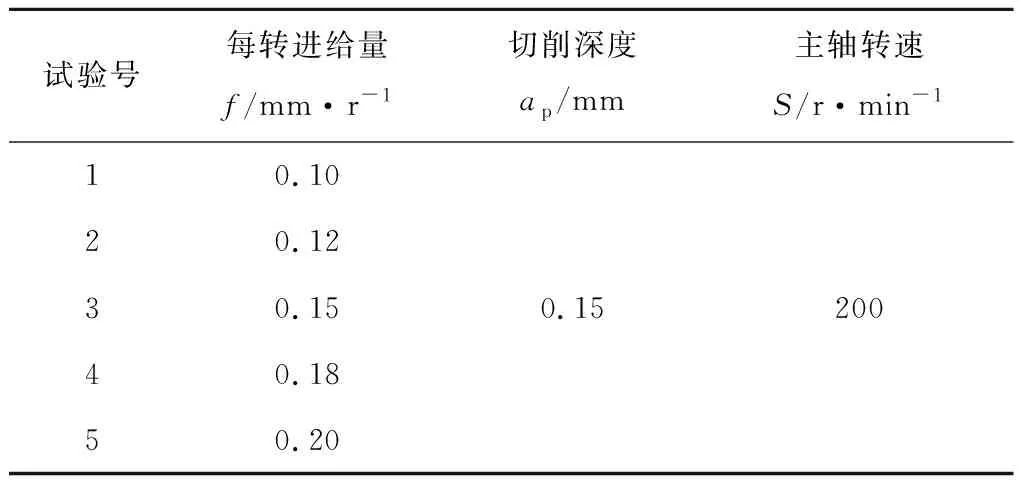
表2 每轉進給量影響試驗表

表3 主軸轉速影響試驗表

完成上述3組仿真分析，得到如下結果(見圖2～圖4)。

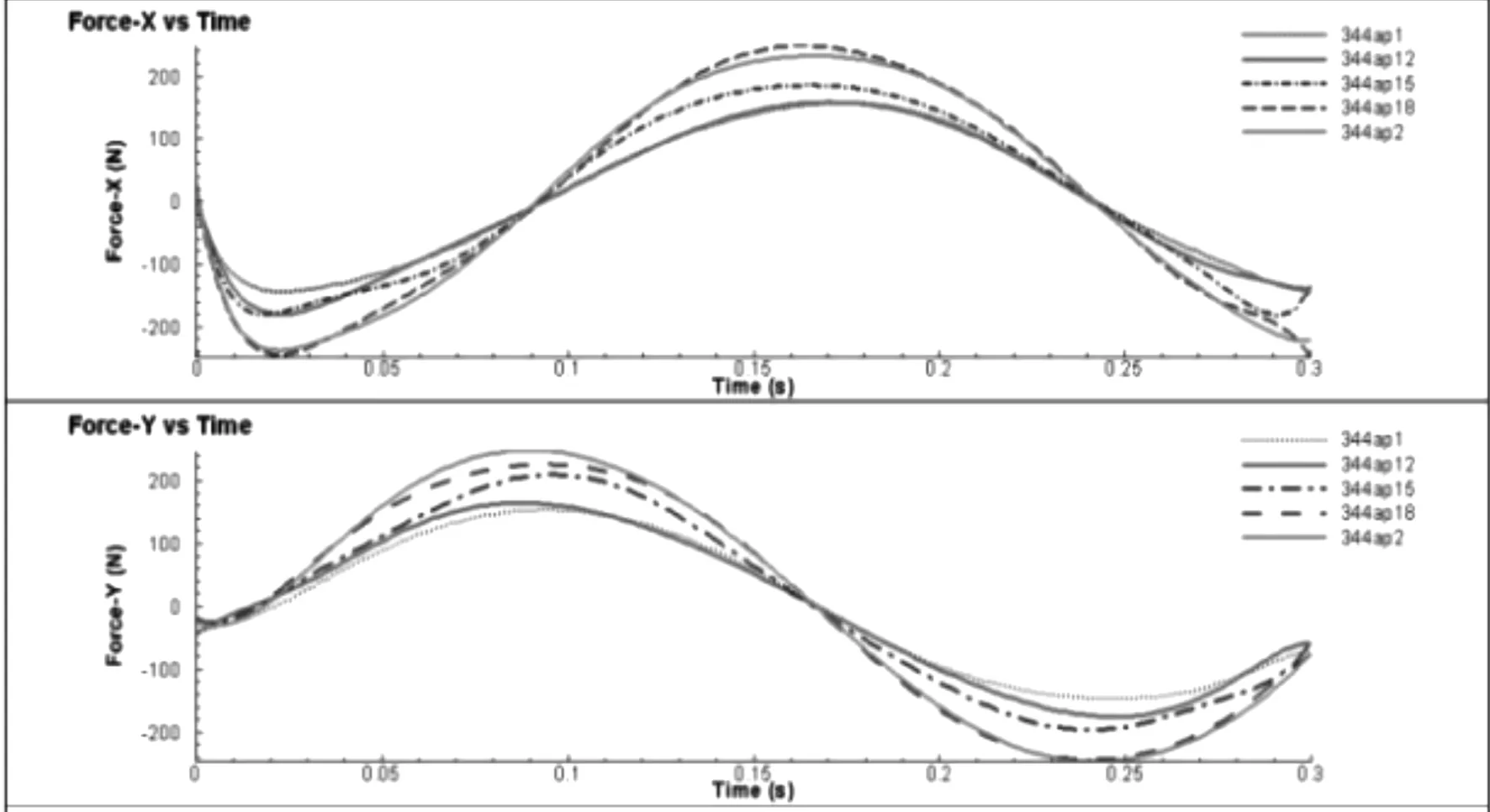
a) 應力曲線圖

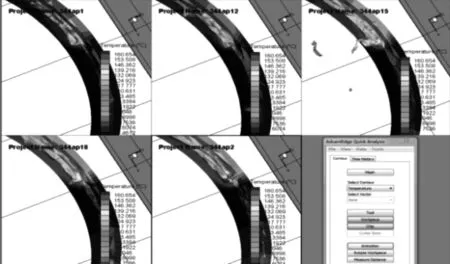
b) 溫度場云圖

c) 第四強度應力云圖

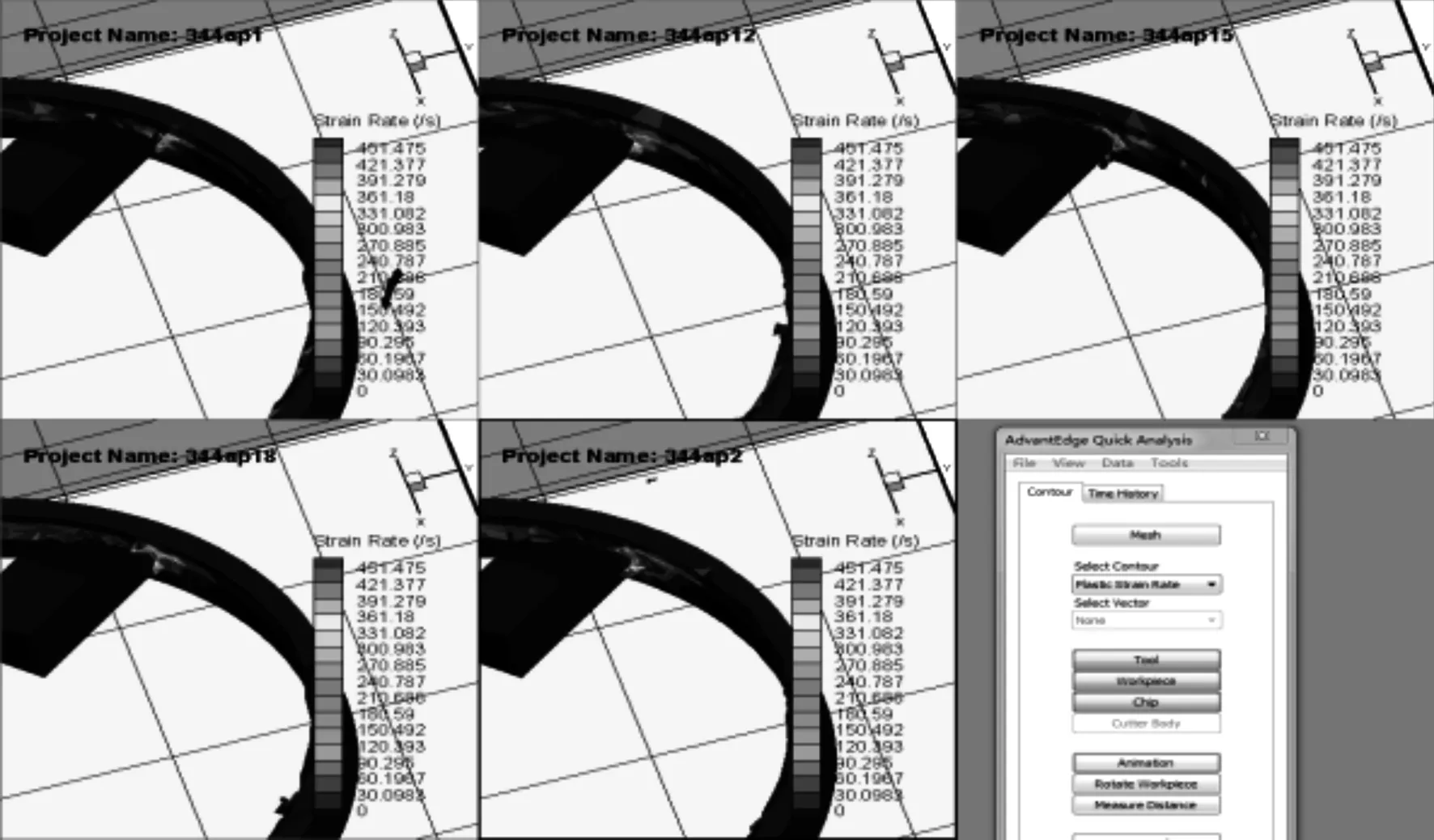
d) 塑性應變率云圖

通過圖2a可發現，隨著切削深度的增大，切削力增大，但ap=0.10 mm與ap=0.12 mm這2條曲線基本重合；由圖2b和圖2c可以看出，ap=0.10 mm、0.12 mm、0.15 mm對溫度場及第四強度應力場影響不大；圖2d顯示出，當ap=0.10 mm和ap=0.12 mm時，塑性應變率影響范圍較小且塑性應變率低。因此，在選取切削深度時，結合加工效率可優先選擇ap=0.12 mm，其次考慮ap=0.15 mm。

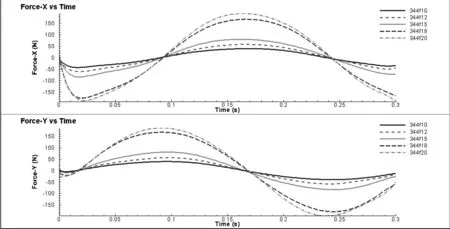
a) 應力曲線圖

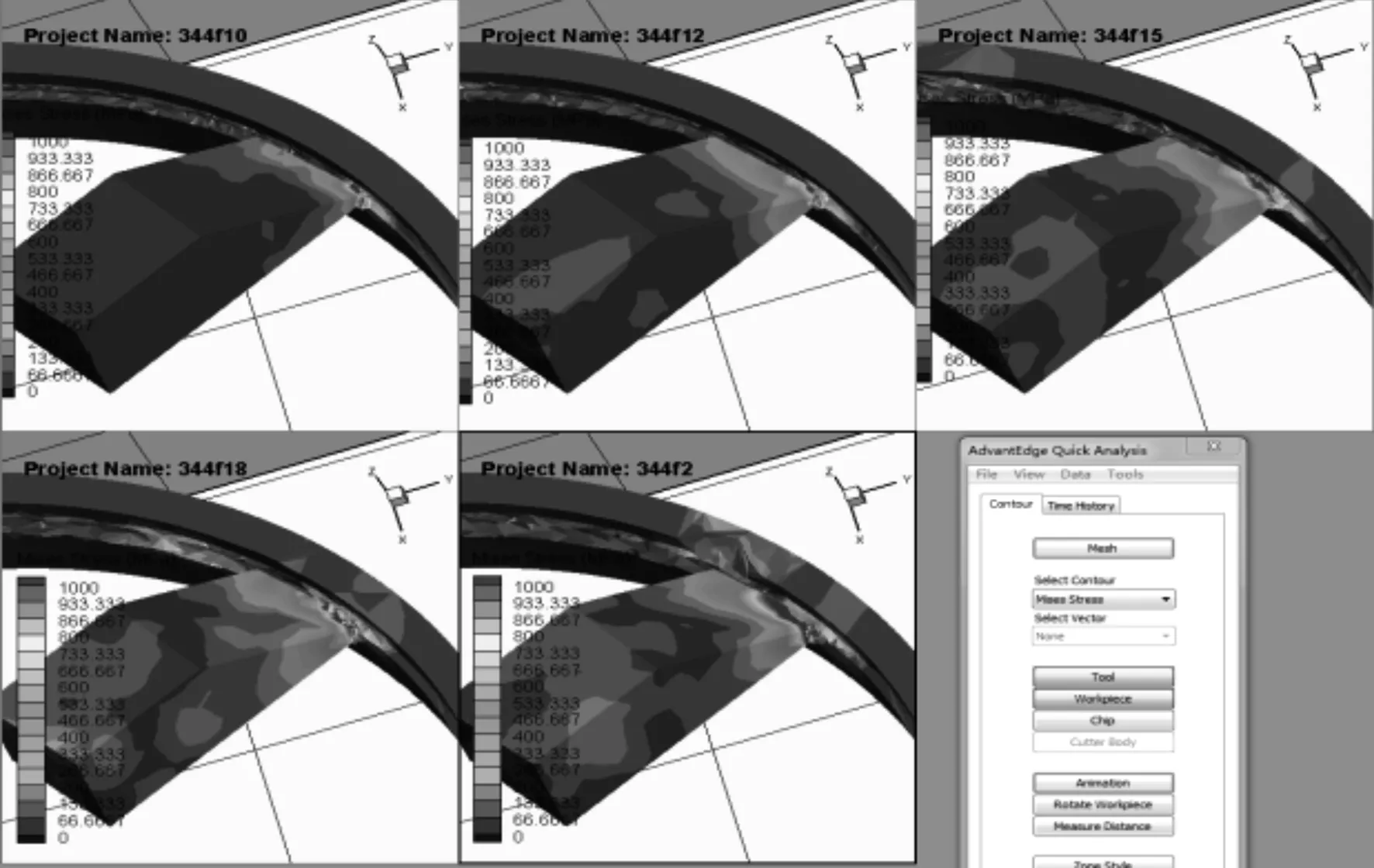
c) 第四強度應力云圖

a) 應力曲線圖

b) 溫度場云圖

c) 第四強度應力云圖

d) 塑性應變率云圖

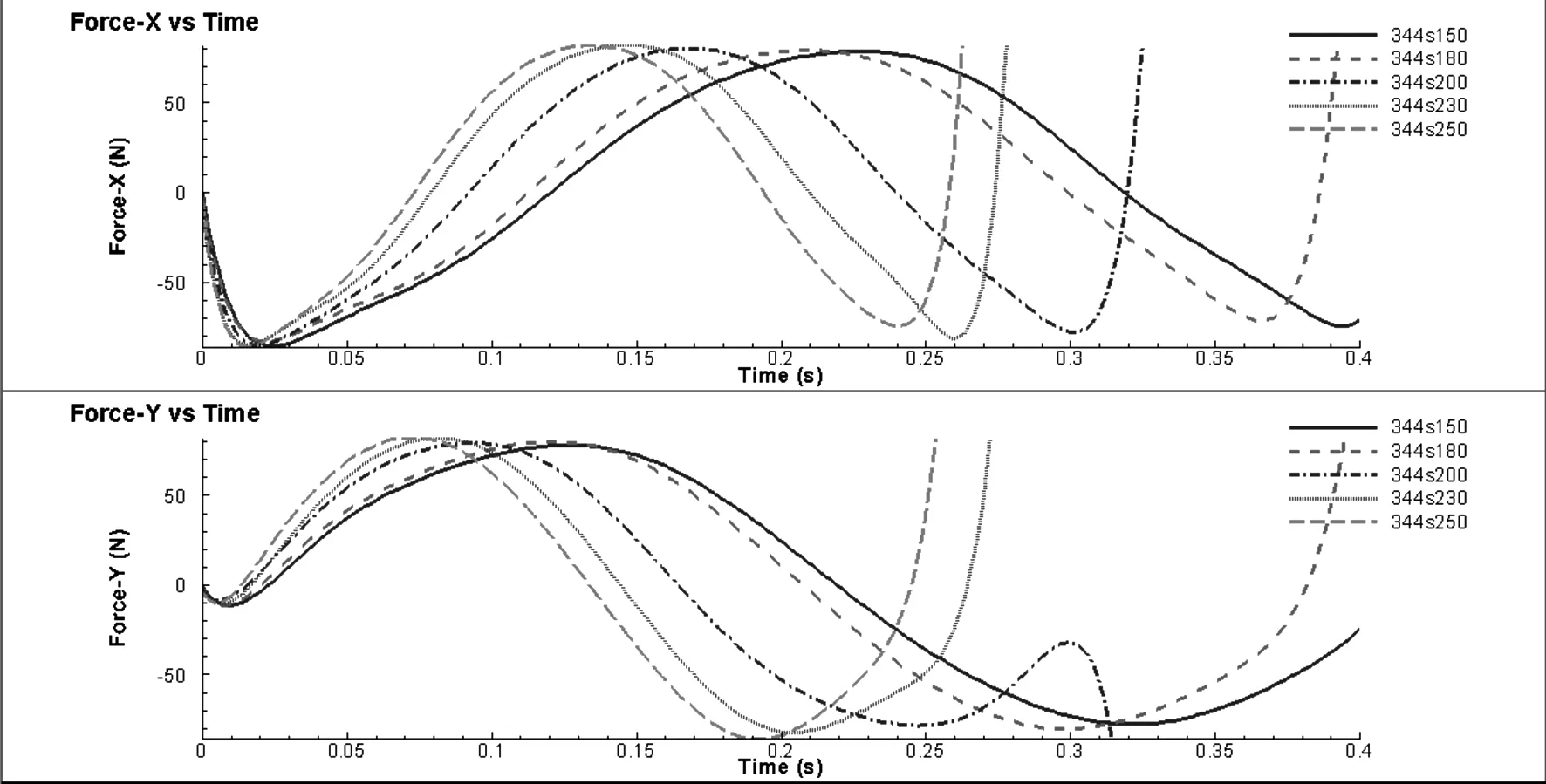
通過圖3a可發現，隨著進給量f的加大，切削力變大，但f=0.10 mm/r、0.12 mm/r和0.15 mm/r條件下應力場變化相對比較平穩，f=0.18 mm/r相較f=0.15 mm/r有突變，在選取切削進給速度時，綜合加工效率和質量，可優先選擇f=0.15 mm/r，其次在后期考慮實際變形情況時在f=0.10 mm/r、0.12 mm/r和0.15 mm/r之間篩選或選取區間值。通過圖3b～圖3d可以看出，f=0.10 mm/r、0.12 mm/r和0.15 mm/r對溫度場、第四強度應力場及塑性應變率影響不大。

通過圖4a可發現，隨著主軸轉速S的加大，切削力變大，考慮到避免切削力的急速變化，選取S=150 r/min和180 r/min。同時考慮加工效率則優先選擇S=180 r/min。通過圖4b～圖4d云圖可以看出，S=150 r/min、180 r/min和200 r/min對溫度場、第四強度應力場及塑性應變率影響并不太大。

綜合上述分析可以看出，隨著切削深度的不斷增加，可以得到各切削分力隨之逐漸遞增，但各有緩急。主切削力對切削深度ap的反應較為靈敏，而其他作用分力對其反應較弱。根據輸出的時間-載荷曲線，可以得到在不同切削深度下的輸出載荷的最大值。具體參數見表4。

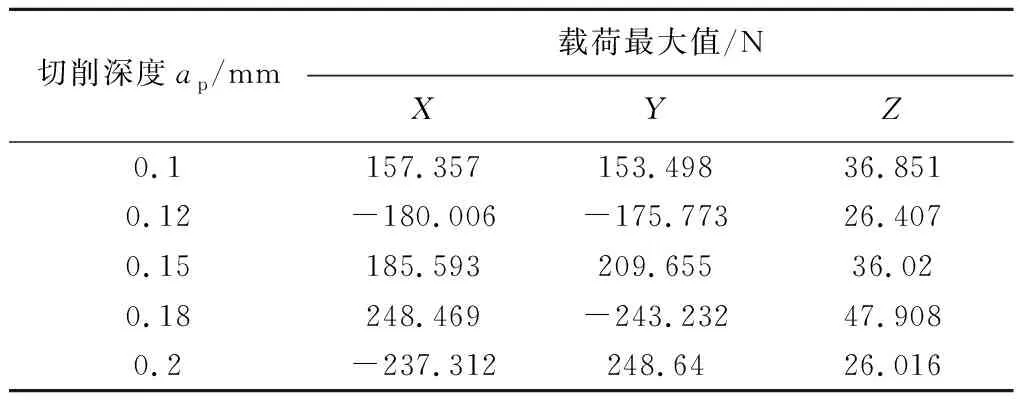
表4 提取數據中的載荷最大值

3 薄壁外殼體結構件加工變形仿真

這部分仿真分析選用通用有限元分析軟件ANSYS-workbench，建立薄壁外殼體零件的有限元模型，將切削力分析結果作為輸入，采用動力學方法得到加工狀態下的響應。將特征簡化的模型導入ANSYS-Workbench有限元模型(見圖5)。

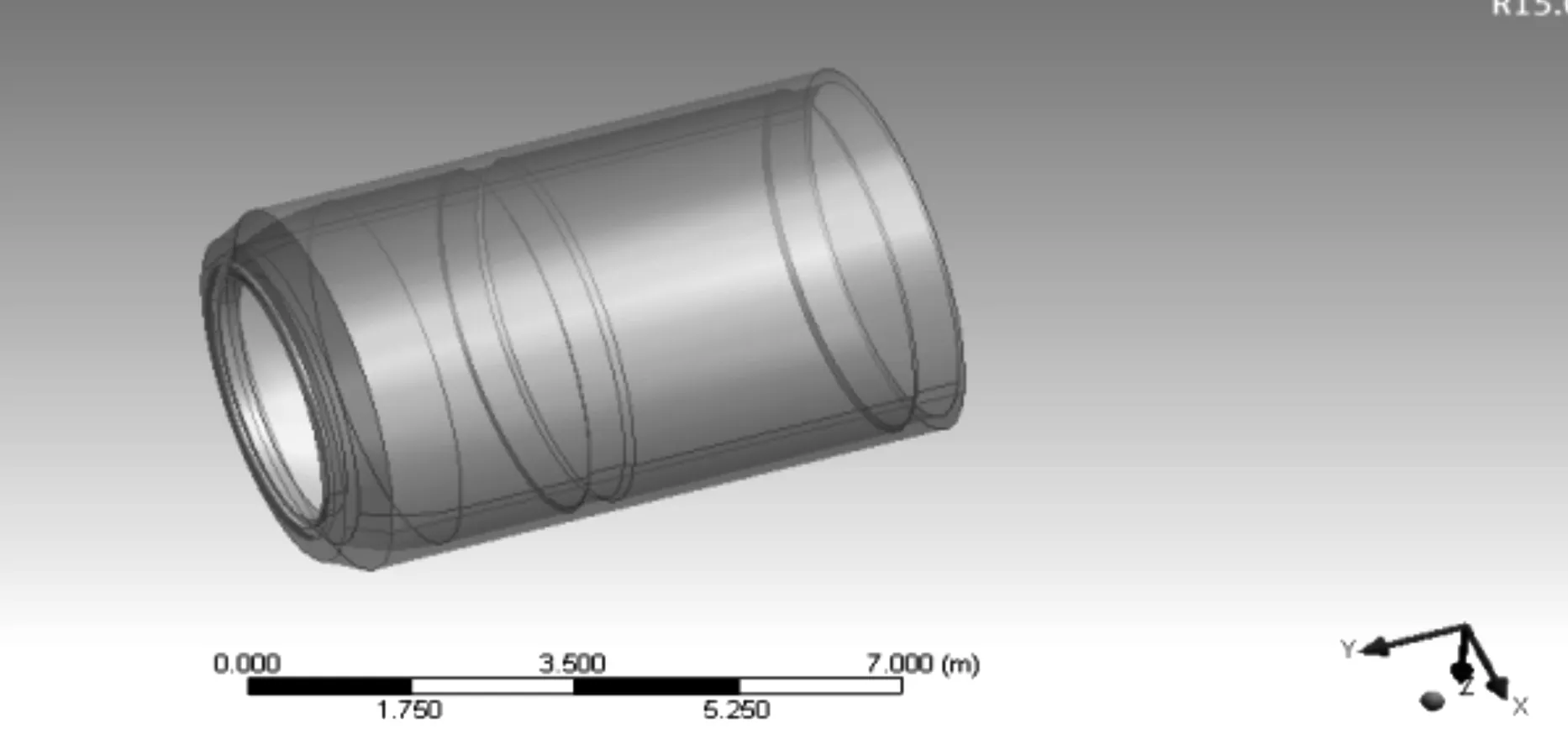
圖5 薄壁結構件簡化有限元模型結構圖

首先對薄壁外殼體零件進行模態分析，采用Block Lanczos法來分析薄壁零件，其計算最為準確和全面[6-7]。計算得到的薄壁零件的前6階固有頻率如圖6所示，前6階模態振型圖如圖7所示。

圖6 前6階固有頻率

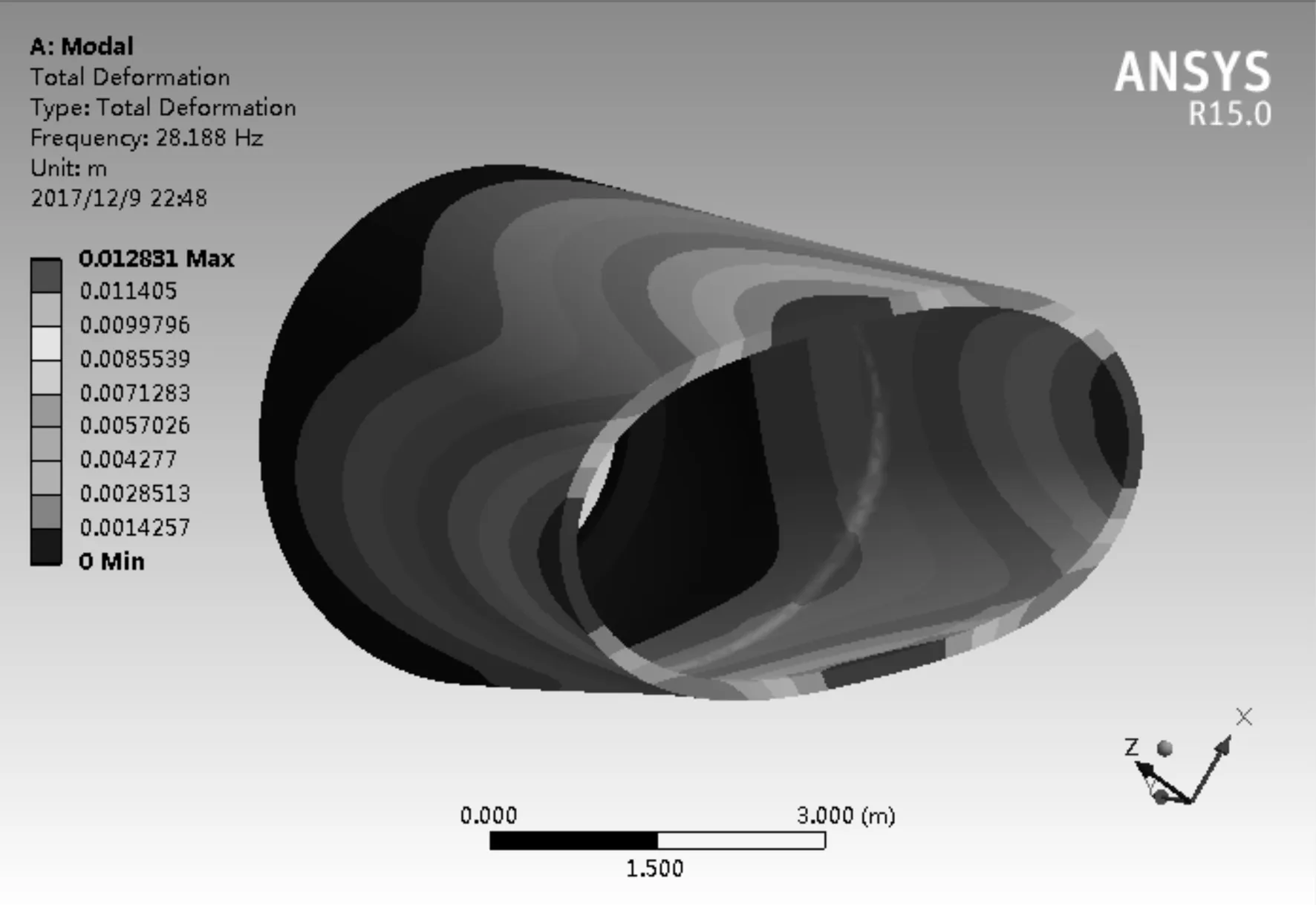
a) 第1階

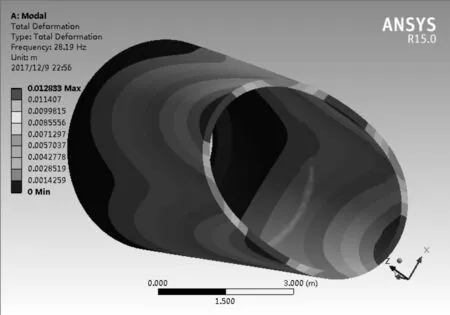
b) 第2階

c) 第3階

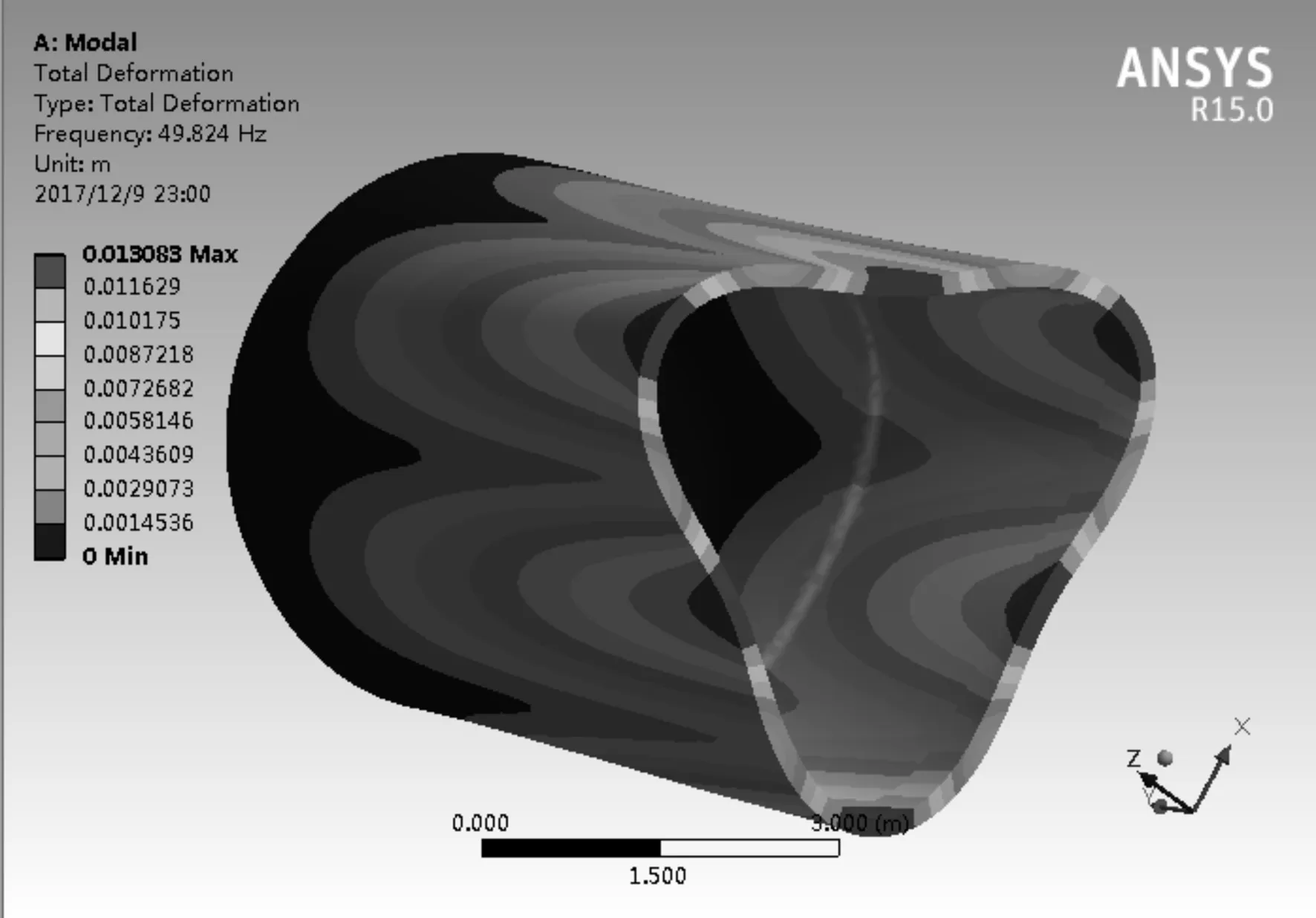
d) 第4階

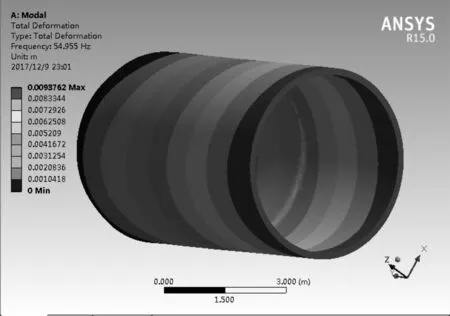
e) 第5階

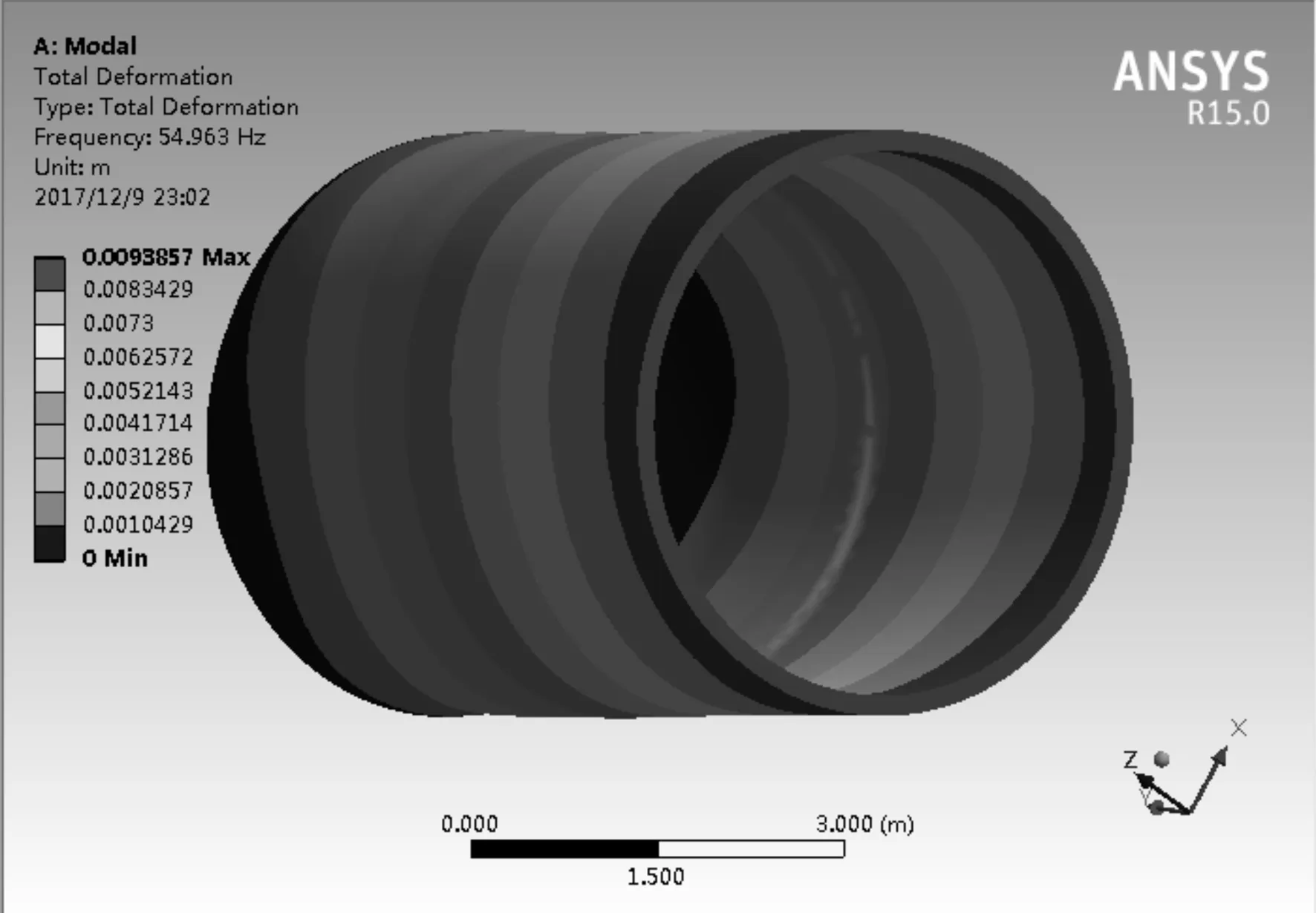
f) 第6階

從圖7中可以得知，薄壁外殼體零件的低階自振頻率主要發生在零件底部圓孔處，這也符合實際加工出現的缺陷。對于一般機械結構而言，其一階固有頻率是影響結構特性的重要指標[8]。根據有限元分析結果，薄壁外殼體零件第1階自振頻率為28.188 Hz，低階自振頻率發生處意味著該處的比剛度較弱，加工中受到交變切削力的作用易發生振動，從而導致加工誤差變大。因此在切削加工中必須確保切削頻率遠離該頻率，以保證加工過程的穩定性。在圖7中的第3階和第4階振型中可以預判，在相應切削頻率下，結構發生6點變形，加工完成后更加不容易對變形進行控制，所以選擇切削力加工頻率時應靠近第1階和第2階模態時的頻率為最佳選擇。

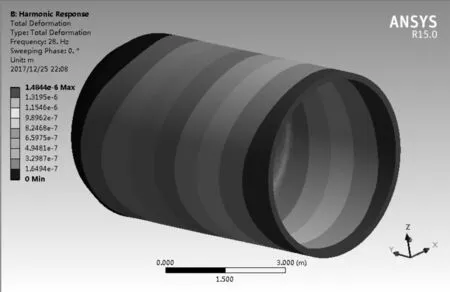
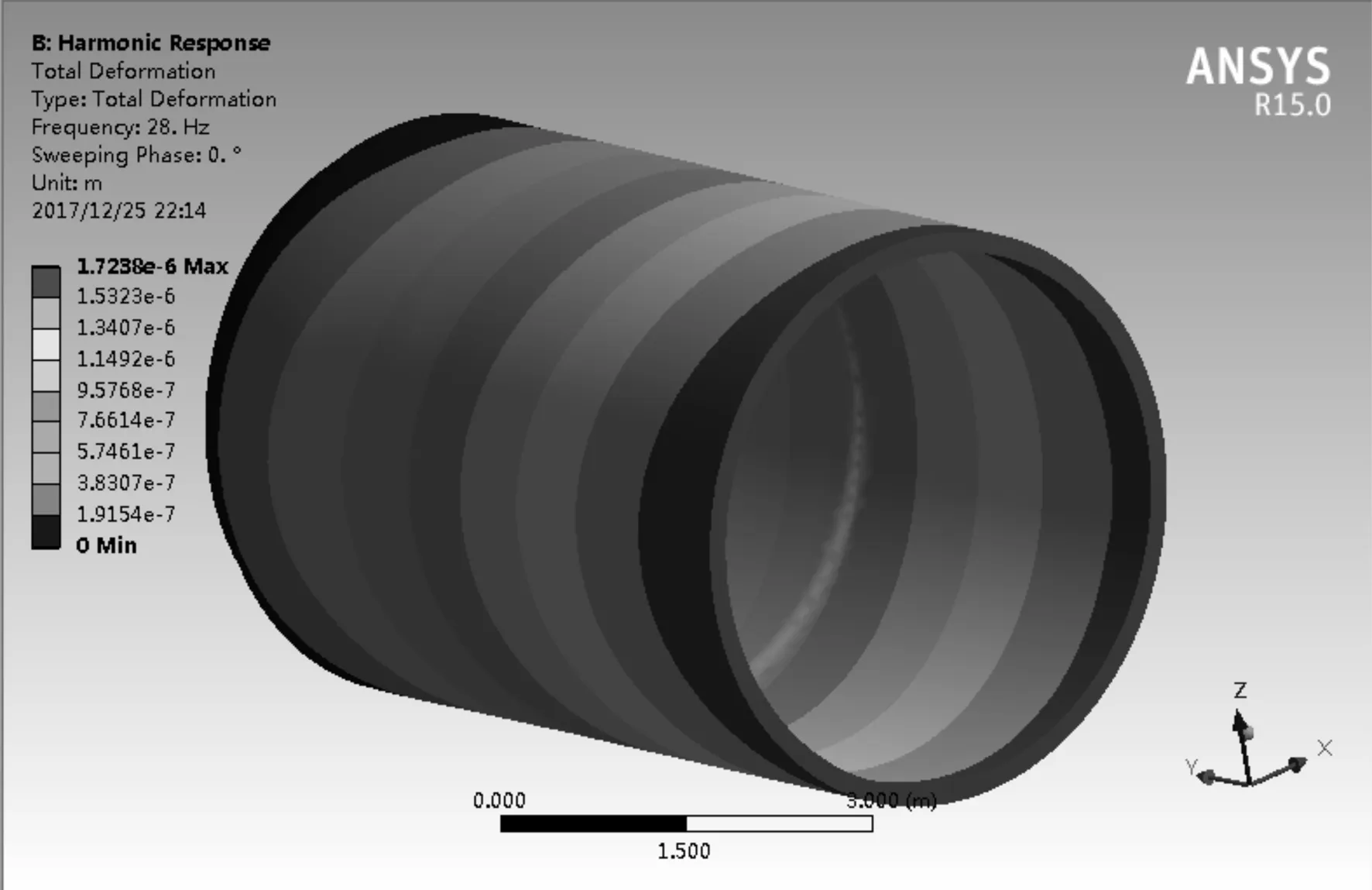
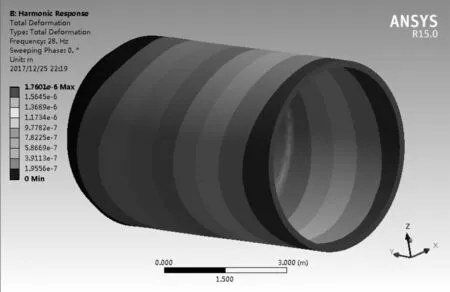
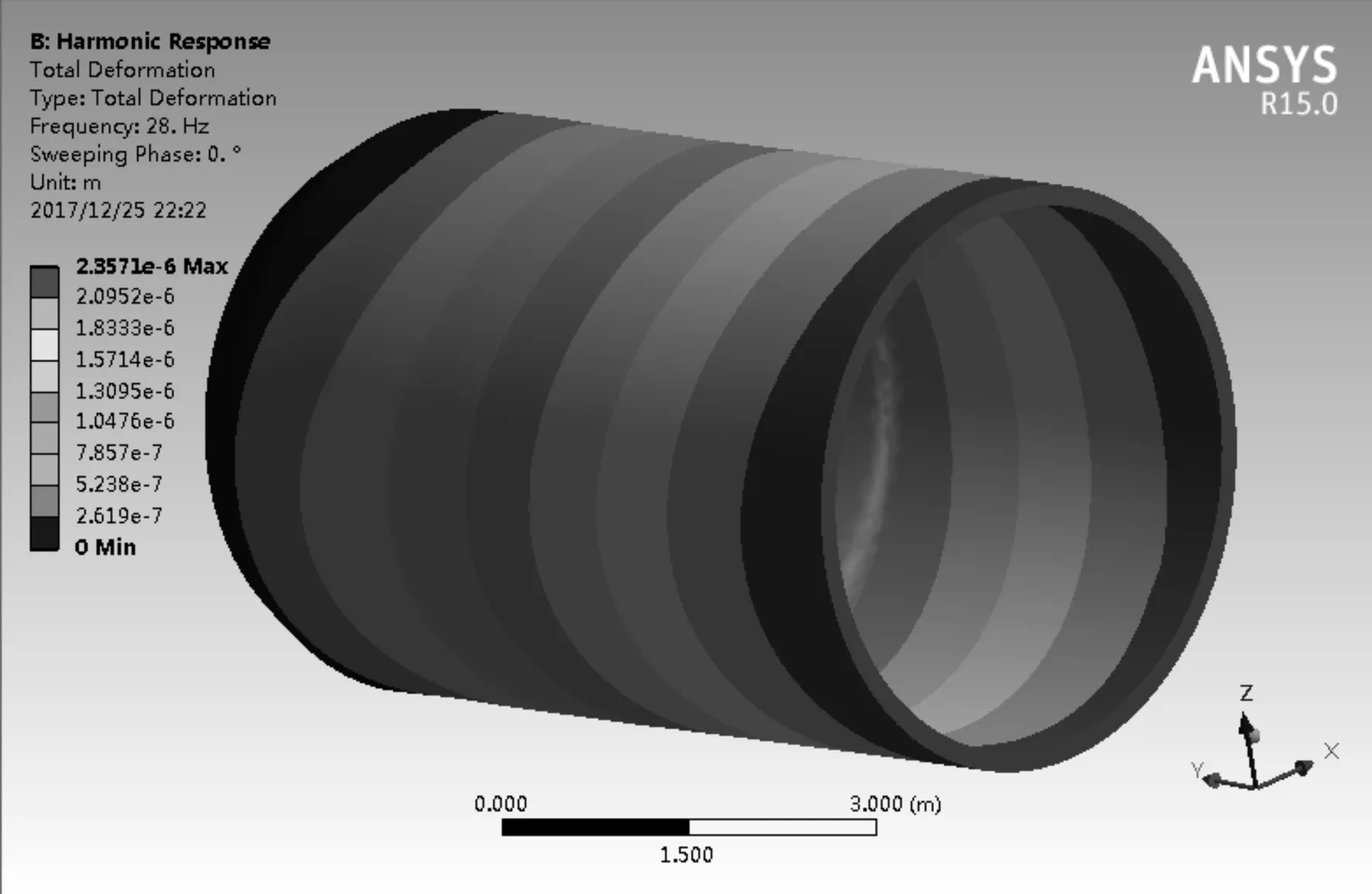
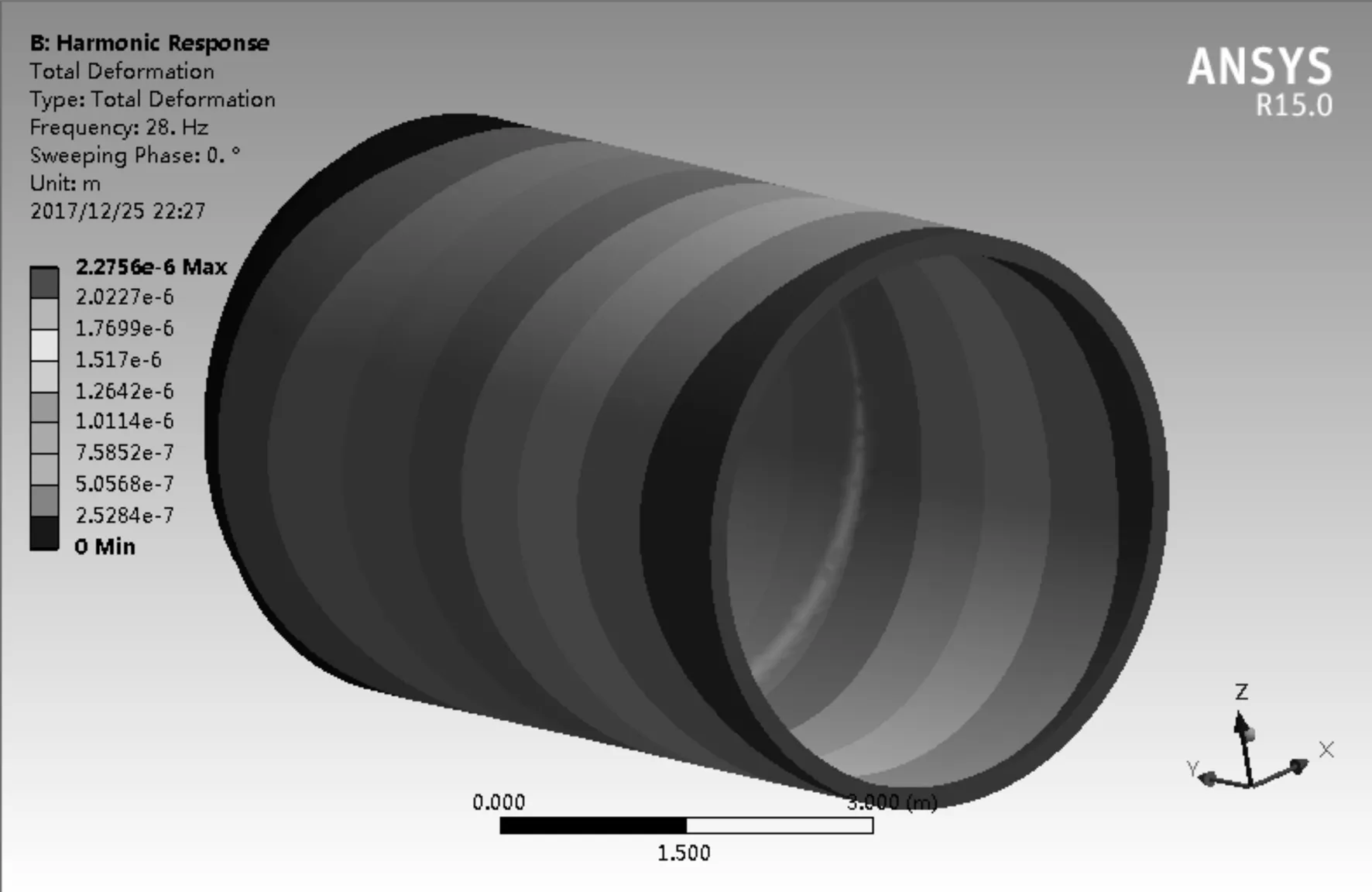
根據模態分析結果圖可知，系統剛度最弱環節在薄壁外殼體零件的底部孔處，車削該部位孔時，在車削力的作用下相當于對工件施加了一個交變作用力，在力的作用下工件產生變形，從而導致加工誤差。將頻率為1.0～28.188 Hz的交變切削力施加在底部孔位置，通過諧響應分析可以得到工件的變形響應[9-10]。

圖8所示為在裝夾狀態下，采用不同的切削深度車削孔時的加工變形云圖，總體變形值最大為ap=0.2 mm時達到單邊0.02 mm，所以直徑方向變形值可達到0.04 mm。通常認為計算值與實際值之間的偏差為10%，而該道工序要求的公差為0～0.063 mm，如果考慮機床自身內部的不平衡及外部傳來的振動干擾，在實際加工時，建議選擇ap=0.15 mm進行加工。

4 結語

通過應用Advantedge FEM軟件對薄壁外殼體件車削加工過程進行仿真分析可知，切削深度及每轉進給量對切削力的影響較大且切削深度的影響最大，主軸轉速對其影響相對較小，并且在一定范圍內，隨著切削深度、每轉進給量的不斷增加，各切削分力不同程度地隨之逐漸遞增。分析得知，切削深度的優選范圍為0.12～0.15 mm，每轉進給量的優選范圍為0.2～0.3 mm/r。后通過ANSYS-workbench對該薄壁模型進行模態分析及諧響應分析得到工件的加工變形情況，可知該狀態下的最優切削深度為0.15 mm。